İki Görüntüden Tekrar Oluşturma (Reconstruction from Two Views)
Problemi formüle edelim. İki faraziyemiz olacak. Faraziyeler şart, çünkü zor problemler ile uğraşıyoruz, ve bazı faraziyeler ile işimizi kolaylaştırmamız gerekli. Araştırmacılara tavsiyem yeni bir problem üzerinde uğraşıyorlarsa ise güçlü faraziyeler ile başlayıp çözüm alanını kısıtlamaları ki bu şekilde çözüm daha rahat bulunabilsin; ve yer geldiğinde kısıtlamalar gevşetilebilir. Bunu vurguladım çünkü bazı öğrencileri görüyorum, herşeyi tek seferde yapmaya uğraşıyorlar, sonra o koca problem için bir program alelacele kodlanıyor, ve program işlemeyince moralleri bozuluyor, vs. Önce kısıtlı başlayın, sonra genelleştirirsiniz.
Faraziyeler şunlar;
İki imajdaki aynı objelerin her iki görüntüdeki ilginç noktalarını ve o aynı noktaların birbirleri ile nasıl eşleştiğini biliyoruz.
İki imaj statik bir dünyayı resmediyor, yani 1. ve 2. görüntü arasında resimdeki objeler hareket etmiyorlar.
Kameranın iç parametreleri sabit ve biliniyor.
Bu bilgilere ve faraziyelere dayanarak ve eğer kameranın izafi yerini ve duruşunu biliyorsak 3D yer bilgisini üçgenleme (triangulation) ile hesaplayabiliriz.
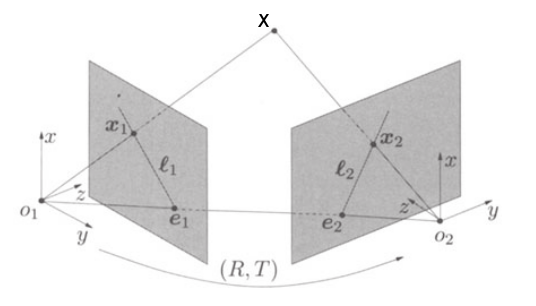
Çözmeye uğraşacağımız bir kameranın dış parametreleri ve görüntüdeki objenin 3D yeri. Elimizde iki resim var, resimdeki ilginç noktaların eşleşmesi var, kameranın katı gövde hareketini, ve \(X\)’i bulacağız.

Üstteki aslında çetin bir tavuk-yumurta problemi. Eğer kamera hareketini biliyor olsaydım iki görüntüdeki eşlemesini bildiğim noktalar üzerinden hemen 3D yer hesaplayabilirdim. Mesela cep telefonlarında artık hareket algılayıcıları oluyor, bu bilgi yeterince kesin olsa \(R,T\)’yi hemen bulmuş olurdum, imajlara bakmak gerekmezdi. O zaman üstteki resimde gösterilen iki çizginin kesiştiği noktayı üçgenleme ile bulurdum, ve 3D noktası \(X\) bulunmuş olurdu. Bu hesap çok basittir. Ya da tam ters yönden, \(X\)’i bir şekilde biliyorsak kamera hareketi hesaplanabilir. Eğer elimizde yeterince nokta var ise çözüm tek olacaktır. 3D tekrar oluşturma hesaplarının zorluğu bu iki bilgiyi de aynı anda kestirmemiz gerektiğidir.
Bu derste takip edeceğimiz yöntem önce kamera hareketini, sonra obje yerini bulmak. Dediğimiz gibi bu problem yumurta-tavuk problemi, fakat bu iki problemin birbiriyle ilişkisini kesmek (decouple) mümkün.
Tipik bir resim üzerinde görelim,

Manzara iki farklı yönden görüntülenmiş. Birinde olan bazı noktalar diğerinde olmayabilir ama çoğu nokta iki tarafta da var. Mesela bir 3D noktası \(P\)’yi düşünelim, bu nokta bir bakış açısında 2D \(x_1\) noktasına, diğerinde \(x_2\) noktasına düşüyor. Kamera merkezleri \(o_1\) ve \(o_2\). İki bakış açılı örnek böyle. Bu derste üstteki gibi, yani iki bakış açı üzerinden hesaplarla oldukça çok uğraşacağız, fakat çoklu bakış açısından da bu hesapları nasıl genelleştirebileceğimizi göreceğiz [dersimizin adına sadık kalmak lazım!].
Notasyonu netleştirelim (üstteki gibi bir resim daha)
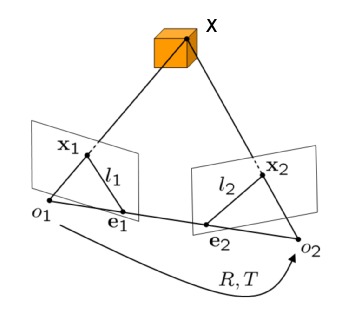
Kamera orijin noktaları \(o_1,o_2\) görülüyor. Bu iki orijini bir düz çizgi ile birleştirelim, bu çizginin her iki görüntü düzlemini kestiği noktalar \(e_1,e_2\) eş kutuplar (epipoles) olarak isimlendirilir. \(X,e_1,e_2\) noktalarının üzerinde olduğu düzlem ise eş kutupsal düzlemdir (epipolar plane).
Notasyon böyle. Peki o zaman tekrar oluşturma (reconsruction) problemini nasıl tanımlarız? Aslında bu problemi bir maliyet (cost) fonksiyonu üzerinden formülize etmek oldukça basit. Bilimde pek çok problem belli bazı parametrelerin hesapsal tahminiyle alakalıdır, ve bu tahmini yapabilmek için tipik olarak bir maliyet tanımlanır, ki bu maliyet fonksiyonu verilen belli parametre değerleri için bu değerlerin iyi mi kötü mü olduğunu cevaplar. Tabii bir sonraki adım o maliyeti minimize etmeye uğraşmak, ve bu minimizasyonu sağlayan “optimal’’ parametreleri bulmaya uğraşmaktır.
Diyelim ki elimizde iki değişik açıdan alınmış görüntüde eşleşmesi yapılmış 100 tane nokta var, \(x_1^j,x_2^j\), \(j \in \{1,..,100\}\), yani \(j\) bir indis. Bu noktalar 3D \(X_j\) noktalarından geliyorlar, tahmin etmeye çalıştığımız onlar - bilinmeyen değişkenler. Ayrıca \(R,T\) de bilinmiyor tabii, 6 tane bilinmeyen değişken de buradan geliyor. Yani bilinmeyen parametreler çok, 100 x 3 (çünkü \(X_1\)’in 3 tane öğesi var) artı 6 tane bilinmeyen var. Optimizasyon bağlamında bu 306 boyutlu bir uzayda iş yapmaya çalışacağız demektir, ve bu pek iyi bir şey değil!
Problemi çözmek için yansıtma hatasını minimize etmeye uğraşabiliriz,
\[ E(R,T,X_1,..,X_{100}) = \sum_{j} || x_1^j - \pi(X_j)||^2 + || x_2^j - \pi(R,T,X_j)||^2 \]
Üstteki formülün eşitliğin sağ tarafının ilk teriminde kendimizi 1. kameranın kordinat dünyasına alıyoruz; 3D \(X\) noktalarını kameraya yansıtıyoruz, ve aradaki hatayı hesaplıyoruz. İkinci terimde 2. kamera kordinat dünyasındayız, aynı \(X\) noktalarını bu sefer rotasyon, yer değiştirme sonrası 2. kameraya yansıttıktan sonra o kameradaki yansıtma hatasını hesaplıyoruz. Minimizasyonun amacı \(E()\) içindeki parametrelerin en optimal olanlarını bulmak ki \(E\) hatası en az olsun.
Üstteki yaklaşıma demet ayarlaması (bundle adjustment) ismi veriliyor; demet çünkü pek çok parametreyi aynı anda vererek optimize etmeye uğraşıyoruz. Tek problem maliyet fonksiyonu içbükey (convex) değil. Optimizasyon dersinden hatırlayabileceğimiz üzere eğer elimizde çok boyutlu ve içbükey olmayan bir problem var ise, bu kötü haber, bu çözümü büyük ihtimalle bulamayacağız demektir. Bilim dalımız aslında hala bu problemi nihai olarak çözmek için yoğun araştırma yapıyor, çünkü çözüm bulunabildiği zaman bile çözüm özgün değil, vs.
Üstteki problemin çözümü için iki değişik yaklaşım var. Birisi problem tanımını olduğu gibi almak, ve bir şekilde “becerikli’’ bir algoritma ile minimizasyonu iyi becermeye uğraşmak. Mesela bir yaklaşıma göre birkaç nokta ile işe başlanır, minimize edilir, sonra ötekiler eklenir ve rafine ede ede nihai sonuca erişilmeye uğraşılır. Eğer varılan sonuçtan memnun olunmadıysa, optimizasyon başlangıç noktası rasgele olarak tekrar seçilir, ve rutin tekrar işletilir, böylece iyi başlangıç noktası ile daha iyi sonuca varılmaya uğraşılır, fakat tahmin edileceği üzere bu kolay bir iş değil.
Bu derste takip edeceğimiz yöntem farklı maliyet fonksiyonlarıyla çalışmak; bu fonksiyonlar orijinal maliyete benzeyecekler, fakat biraz daha basit oldukları için minimize edilmeleri daha kolay olacak. Mesela \(R,T\) ile \(X\) noktalarının arasındaki ilişki kesilecek, bu parametreler ayrı ayrı optimize edilecek. Bu ilişki kesimi nasıl oluyor? Biraz sihirli bir yaklaşım gibi geliyor kulağa, kullanacağımız numara eş kutupsal kısıtlama (epipolar constraint) kavramını devreye sokmak, böylece 8-nokta algoritmasını (8-point algorithm) elde etmiş olacağız.
Kamera matrisi \(K\)’nin bilindiğini varsayıyoruz. Ayrıca \(K = 1\) alacağız, yani her şeyin kameranın odak uzaklığının birimi üzerinden tanımlı olduğunu farzedeceğiz. Birinci kamera için sadece bilinmeyen derinlik bilgisi bilinmeyen bir yansıtma var. İkinci kamera için rotasyon ve yer değiştirme sonrası ardından bir yansıtma var. Yani,
\[ \lambda_1 x_1 = X, \qquad \lambda_2 x_2 = RS + T \qquad (1) \]
Resim üzerinde
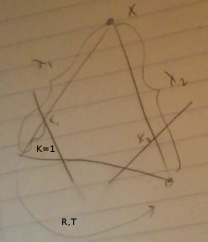
Yani \(X\)’den \(x_1\)’e gelmek demek sadece \(\lambda_1\) ile ölçeklemektir. Aynı durum dönme ve yer değişim sonrası \(x_2\) için de geçerli. Tatmin etmemiz gereken iki denklem bunlar. Bu iki denklemi birleştirerek ve diğer noktaları ekleyerek yavaş yavaş \(X\)’i dışarı atmaya uğraşacağız. İlişki kesmeyi bu şekilde yapacağız. 1. denklemi 2. denklem içine koyalım,
\[ \lambda_2 x_2 = R(\lambda_1x_1) + T \]
İki tarafı soldan \(T\)’nin eksi bakışımlı hali \(\hat{T}\) ile çarpalım (\(\hat{T}v \equiv T \times v\)). Niye? Çünkü biliyoruz ki bir vektörün kendi eksi bakışımlı matrisi ile çarpımı sıfırdır (ya da vektörün kendisi ile çapraz çarpımı sıfır verir), böylece eşitliğin sağındaki \(T\)’den kurtulmaya uğraşıyoruz. O zaman
\[ \lambda_2 \hat{T} x_2 = \lambda_1 \hat{T} R x_1 \]
Böylece \(T\)’den kurtulmuş olduk, aynı zamanda \(X\)’den de kurtulmuş olduk. Dolaylı olarak \(X\) hala formülde tabii, çünkü \(\lambda_1\) ve \(\lambda_2\) 3D noktaya olan uzaklıklar, ve \(\lambda_1 x_1\) mesela bize 3D noktasını verir.
Devam edelim, üstteki ifadeyi \(x_2\)’ye yansıtalım. Niye? Çünkü üstteki eşitliğin sol tarafındaki \(\hat{T}x_2\) bir çapraz çarpım, ve bu çapraz çarpım bize \(x_2\)’ye dikgen bir vektör verir, ve eğer bu vektörü \(x_2\)’ye yansıtırsam sıfır elde ederim, yani sol taraf yokolur. Ayrıca \(\lambda_1\) ile bölerim. Geri kalanlar,
\[ x_2^T \hat{T} R x_1 = 0 \]
olur. Buna eş kutupsal kısıtlama ismi veriliyor. Formül ilginç çünkü iki 2D noktası \(x_1,x_2\) ve döndürme, yer değiştirme arasında bir ilişki kuruyor, 3D nokta bilgisi ortada yok. Bu bize bir kabiliyet kazandırdı, buradan hareketle diğer bilinen 2D nokta eşlerini alarak, ve üstteki sınırlamayı kullanarak bilinmeyen \(R,T\)’yi hesapsal tahmin etmeye uğraşabilirim.
(1)’den üstteki formüle gelmek için bazı transformasyonlar yaptık, bunlardan bazılarının tersi alınabilir olmadığına dikkat; mesela son adımda \(x_2\)’ye yansıtma yaptık, bu durumda \(x_2\)’e dikgen olan bilgi yokolmuş oldu. Ya da \(\hat{T}\) ile çarpım işlemi - \(\hat{T}\) tersi alınabilir bir matris olmadığı için bu işlemi de geriye almak mümkün değil. Yani son iki adımın ikisinde de bir şeyler kaybetmiş oluyoruz aslında. Tabii kaybettiklerimiz yanında kazandıklarımız var, daha önce belirttiğimiz gibi, 3D bilgisi ile uğraşmak zorunda değiliz artık. Belli kısıtlamalarla işe başladık, bazı transformasyonlar sonunda daha zayıf bir kısıtlama elde ettik, ama bir avantaj elde ettik.
Üstteki önemli bir formül, biraz daha üzerinde durmak iyi olur. Formüle bazen gerekli kısıtlama (essential constraint) ya da iki lineerli kısıtlama (bilinear contraint) deniyor. Ayrıca formülün ortasındaki \(\hat{T} R\) çarpımına, ki bir \(3 \times 3\) matristir, gerekli matris (essential matrix) ismi veriliyor.
Genel kural olarak bir kavrama bir isim verilmişse, hatta birden fazla isim verilmişse, o konunun önemli olduğunu ve çoğu zaman pek çok kişi tarafından araştırılmış olduğu sonucuna varabiliriz.
Kolaylaştırmalar ardından buraya geldik, fakat \(R,\hat{T}\) çözümü hala zor; \(E = \hat{T}R\) bilindiği durumda bu çarpımdan \(\hat{T}\) ve \(R\)’yi nasıl çıkartacağız?
O hesaba gelmeden önce eş kutupsal kısıtlamanın geometrik anlamına yakından bakalım. Amacımız bir düzlem tanımlamak, ve düzlemin olma şartını eş kutupsal sınırlamaya bağlamak.
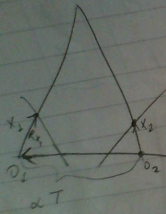
Eğer 1. kamera orijin kabul edilirse \(x_1\)’e giden vektör \(\vec{o_1x_1}\) olur, ya da sadece \(x_1\). Bu vektörü 2. kamerayı orijin olacak şekilde transforme edersek \(Rx_1\). Bir diğer vektör 2. kamera orijinli \(x_2\) noktası / vektörü. Ayrıca \(o_2\) çıkışlı ve \(T\)’ye oranlı (proportional, \(\propto\) işareti oradan geliyor), bir vektör daha var. Bu üç vektör üzerinden (üçlü çarpımla -triple product-) bir paralelepipe hacmi hesaplanabilir, ve eş kutupsal kısıtlama formülünün söylediği bu hacmin sıfır olmasıdır, yani bir düzlem olmasıdır (sıfır hacimli obje düz demektir)
\[ hacim = x_2^T (T \times Rx_1) = 0 \]
ki o da dolaylı olarak \(o_1,o_2\)’den çıkan ve \(x_1,x_2\)’den geçen huzmelerin bir yerde birleşiyor olmaları anlamına gelir. Artık 3D noktadan bahsetmeye gerek yok, sadece iki huzmenin kesişiyor olması yeterli. Kesişiyorlarsa bir düzlem vardır, kısıtlamanın söylediği de budur.
Gerekli matris \(E = \hat{T}R\) demiştik, tüm gerekli matrislerinin uzayı gerekli uzay olarak adlandırılır,
\[ \varepsilon \equiv \bigg\{ \hat{T}R \mid R \in SO(3), T \in \mathbb{R}^3 \bigg\} \]
\(E\)’den \(\hat{T},R\) çıkartmak matris ayrıştırması çağrışımları yapıyor olabilir; ve hakikaten de Huang ve Faugeras’ın 1989 tarihinde ispatladığı bir teoriye göre sıfır olmayan bir \(E \in \mathbb{R}^3\) matrisi bir gerekli matristir sadece ve sadece \(E = U \Sigma V^T\) şeklinde bir Eşsiz Değer Ayrıştırması (Singular Value Decomposition -SVD-) var ise, ve bu ayrıştırma \(\Sigma = diag\{\sigma,\sigma,0\}\) olmalı, \(\sigma > 0\) için, \(U,V \in SO(3)\).
Bu teori gerekli matrisler ve SVD arasında bir eşdeğerlik (equivalence) tanımlamış oluyor, gerekli matrislerin SVD’si olmalı, ve bu SVD’nin iki eşsiz değeri olmalı, en küçüğü sıfır, en büyüğü \(\sigma\) olacak şekilde ve ondan iki tane var. Bu çok faydalı çünkü sonuç itibariyle olabilecek mümkün matris seçeneklerini daraltmış oluyor, ki bu iyi. Gerekli matrisi hesaplayan optimizasyonumuz bu bilgiyi kullanabilir.
Bir sonraki adım eldeki bir gerekli matristen rotasyon ve yer değişimi çıkartmak. Ufak bir problem - bu sonuç özgün değil, pratikte 2 tane mümkün çözüm olabilir. Ama iyi haber \(E = U\Sigma V^T\) sonrası alttaki çözümlerden sadece biri anlamlı pozitif derinlik bilgisi verir.
\[ (\hat{T}_1,R_1) = (UR_Z(+\pi/2)\Sigma U^T, UR_Z(+\pi/2)V^T) \]
\[ (\hat{T}_2,R_2) = (UR_Z(-\pi/2)\Sigma U^T, UR_Z(-\pi/2)V^T) \]
Formüller biraz çetrefil gözüküyor, evet. İspat için [1, sf. 116]. Yani eğer gerekli matrisi tahminsel hesaplayabiliyorsak, onu kullanarak rotasyon ve yer değişimini üstteki formüllerle hesaplayabiliriz.
Algoritma
Bir 3D tekrar oluşturma algoritması şöyle olabilir; iki görüntüdeki birbiriyle bağlantılı 2D noktalar birbirleriyle eş kutupsal kısıtlama üzerinden ilişkideler. O zaman
Belli sayıda eşlenmiş noktayı kullanarak eş kutupsal kısıtlama üzerinden \(E\)’yi hesapla.
\(E\)’den \(R,T\)’yi hesapla.
Adım #2 için iki seçenek var. Birincisi direk \(E\)’yi hesaplamak, ama bu matrisin gerekli (essential) uzayda olma zorunlulu olduğu için onu gerekli uzaya yansıt. Yine bir pürüz; Biliniyor ki bu yöntem optimal altı (suboptimal). Diğer seçenek eş kutupsal kısıtlamalardan \(E\)’yi hesaplarken o optimizasyon içinde ek bir kısıtlamayla çözümü gerekli uzayda olmaya zorlamak.
Pratikte ikinci seçeneği kodlamak külfetlidir, çünkü bu bir gayrı lineer, dertli kısıtlı optimizasyon, ayrıca ek kısıtlamalar SVD’nin her üç eşsiz değeri üzerinde olmalıdır… Biz lineer, lineer cebirsel bir yaklaşım tercih ediyoruz.
8-Nokta Algoritması
Algoritmanın ismi en az 8 noktaya ihtiyaç duymasından geliyor. Bu algoritma için \(x_2^TEx_1 = 0\) kısıtlamasını farklı bir şekilde tanımlamaya çalışacağız.
Bu kısıtlama \(E\) merkezli bir ikili lineerlik (bilinear) içeriyor. Bu ne demektir? Bir tekrar düzenleme ile bu kısıtlama ifadesini “\(E\)’nin öğeleri çarpı \(x_1,x_2\) öğeleri’’ şeklinde ifade edebiliriz demektir. Bunun için önce \(E\) matrisinin öğelerini”açarak’’’ düz bir vektör içine dizelim. Üstsimge \(s\) hatırlarsak yığma (stacking) operatörüydü,
\[ E^s =\left[\begin{array}{ccccccccc} e_{11} & e_{21} & e_{31} & e_{12} & e_{22} & e_{23} & e_{31} & e_{32} & e_{33} \end{array}\right]^T \in \mathbb{R}^9 \]
olacak. Şimdi
\[ a \equiv x_1 \otimes x_2 \]
tanımlayalım, ki \(\otimes\) Kronecker çarpımı. \(x_i = \left[\begin{array}{ccc} x_i & y_i & z_i \end{array}\right]^T\) üzerinden üstteki çarpımın açılımı
\[ a = \left[\begin{array}{ccccccccc} x_1x_2 & x_1y_2 & x_1z_2 & y_1x_2 & y_1y_2 & y_1z_2 & z_1x_2 & z_1y_2 & z_1z_2 \end{array}\right]^T \in \mathbb{R}^9 \]
Bu tanımlar sayesinde eş kutupsal kısıtlama
\[ x_2^TEx_1 = a^TE^s = 0 \]
olarak yazılabilir. Böylece bilinen değişkenleri bilinmeyenlerden net bir şekilde ayırmış olduk, bilinen her şey \(a^T\) içinde, bilinmeyenler \(E^s\) içinde. Ayrıca kısıtlama bir skalar çarpım haline geldi, ve bu çarpımın söylediği bir şey var, sonuç sıfır olduğu için \(a,E^s\) birbirine dikgen (orthogonal) vektörler. Eşlenmiş bir çift 2D nokta için yapılanlar bunlar. Tüm \(n\) nokta çiftleri için üstteki denklemi bir lineer sistem haline getirebiliriz,
\[ \chi E^s = 0, \qquad \chi = \left[\begin{array}{cccc} a^1 & a^2 & \dots & a^n \end{array}\right]^T \]
Yani \(\chi\) içinde \(a\) vektörleri bir kolon olarak yanyana diziliyorlar. Lineer Cebir dilinde “\(E\)’nin ne olduğunu bilmiyoruz ama biliyoruz ki o \(\chi\)’in sıfır uzayında yaşıyor’’ diyebiliriz. Bir pürüz bu sıfır uzayından gelen çözümün özgün olmaması. \(\chi E^s = 0\)’i tatmin eden herhangi bir çözüm vektörünün katları da çözümdür, yani sonsuz tane çözüm vardır.
Bunun negatif sonucu ölçek bilgisini, 8 ya da kaç tane nokta daha olursa olsun hiçbir zaman gerçek ölçekte tahmin edemiyor olacağımız. İki ev resmine bakıyoruz mesela, fakat belki maket bir evin resimleri bunlar! Robot kodlamasına bu problem çok ortaya çıkar, mesela biz görsel kamera ile yol bulan bir quadcopter kodu geliştirdik, ek olarak sonar algılayıcısı eklememiz gerekti ki bu eksik olan ölçek bilgisini elde edebilelim.
Pratikte hesapları kolaylaştırmak için \(o_1o_2\) uzaklığı 1’e eşitlenir, yani birim \(o_1o_2\) uzaklığı haline gelir; hesapların sonucu bu birim üzerinden raporlanmış olur.
Fakat pozitif yönde şu da var; sıfır uzayının tek boyutlu olmasını garantileyebilirsek, evet oradaki çözümün katları da çözümdür ama en azından ölçekleme problemi tamir edilince elimize tek çözüm geçer. Bunu garantileyebiliriz; en az 8 nokta gerekliliği (ve algoritmanın ismi) buradan geliyor. Bunun için \(\chi\)’nin kertesi tamı tamına 8 olmalıdır. Eğer 8’den daha fazla eşli nokta var ise bunun zararı yok. Ama daha az var ise, mesela 7, o zaman sıfır uzayı iki boyutlu olurdu, ve özgün çözüm elde edilemezdi.
Patajolik durumlarda 8’den daha fazla nokta çifti bile özgün nokta bulmaya yetmez; mesela tüm noktaların 3D dünyada aynı düzlem üzerinde olduğu durumda. O zaman çözüm dejenere çözümdür, çünkü \(a^i\) vektörleri birbirinden bağımsız değildir. Örnek olarak mesela ev resminde 2D nokta çiftlerinin hepsi evin ön duvar üzerinden alınmış ise, bu problem çıkartır. Ama bazı noktalar evin ön duvarı, diğerleri yoldan, diğerleri evin arkasındaki ağaçtan, vs. geliyor ise 8-nokta algoritması düzgün işler.
\(E\)’nin artı ya da eksi işareti tekrar oluşturulamıyor. Her \(E\) için iki \(R\) iki de \(T\) mümkündür, yani mümkün \(R,T\) çiftleri 4’tür. Ama pratikte \(E\)’nin işaretini bulmak kolaydır.
Ayrıca, daha önce söylediğimiz gibi, çoğunlukle hesaplanan \(E^s\) öğeleri bir gerekli matrise tekabül etmez, bir gerekli matrisi bulmak için \(E^s\)’i gerekli uzaya yansıtmamız gerekir, yani en yakın gerekli matrisi hesaplamamız gerekir.
\(\chi E^s = 0\) hususunda bir nokta daha, eşlemelerde hata olabileceği için bu ifade tam olarak çözülemeyebilir. O zaman, ona en yakın olabilecek çözüme erişmeye uğraşırız; yani \(||\chi E^s||^2\)’yi en az kareler bağlamında minimize edecek \(E^s\)’i hesaplarız. Bu minimizasyon \(E^s\)’i \(\chi^T\chi\)’nin en ufak özdeğerine tekabül eden özvektörü olarak seçmek ile mümkün olabilir. Tabii \(\chi^T\chi\) özvektör hesabı ile \(\chi\) eşsiz değer ayrıştırmasının ilişkisi var, bkz [2], ve [3].
Yansıtma için kullanacağımız teorinin ispatı [1, sf. 119]’da. Herhangi bir \(F\) matrisini alalım, ki bu matrisin SVD’si
\[ F = U \textrm{diag} \{ \lambda_1,\lambda_2,\lambda_3\} V^T \]
olsun,
\[ \lambda_1 > \lambda_2 > \lambda_3 \]
olmak üzere. O zaman Frobenius normu \(|| F - E||_f^2\)’i minimize eden matris \(E\)
\[ E = U \textrm{diag} \{ \sigma,\sigma,0 \} V^T , \qquad \sigma = \frac{\lambda_1+\lambda_2}{2} \]
Yani \(F\)’nin SVD’sini alıp buradan gelen en büyük iki eşsiz değerinin ortalamasını \(E\)’nin SVD’sindeki en büyük iki eşsiz değer yapıyoruz, \(E\)’nin en küçük eşsiz değerini sıfır kabul ediyoruz, bu kadar. Niye bu basit ortalamanın işlediği teorinin ispatında.
Algoritma 8nokta \(\left(x_1^i,x_2^i\right)\)
return \(R,\hat{T}\)8’den daha az nokta mümkün mü? Evet. [Atlandı]
Eğer sadece rotasyon var ama yer değiştirme yok ise, 8-nokta algoritması işlemez, çünkü o zaman \(\hat{T}\) sıfır olacak, gerekli matris te sıfır olacak. Bu tür durumlar hiç yok değil, tatilde çekilmiş fotoğraflarda oluyor (hoca sadece kendi etrafında dönerek ardı ardına fotoğraf çeken turist taklidi yapıyor, bu durumda yer değişimi yok, rotasyon var.
[statik olmayan manzara yorumları atlandı]
Kaynaklar
[1] Sastry, An Invitation to 3-D Vision
[2] Bayramlı, Lineer Cebir, PCA
[3] Bayramlı, Lineer Cebir, Rayleigh-Ritz Teoremi