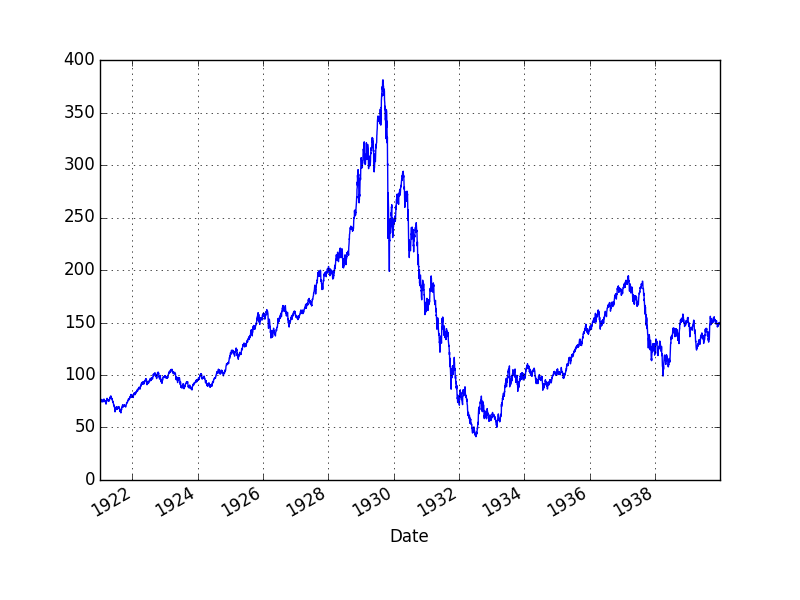
Ekonomik krizlerin finans bağlamında kriz öncesi piyasalarda balon oluşturduğu iddia edilir; mesela ABD'nin 1929, 1987 krizleri, borsalardaki aşırı çıkışlar ardından düşüş ile başlamıştır, en son 2008 krizi öncesi emlak piyasasında balon oluşmuştur. Aynı dinamik tek bir sektör endeksi, ya da tek senet bazında da görülebilmektedir. Demek ki bu tür dinamiği anlayabilmek, tanıyabilmek, hatta nihai gidişatını tahmin edebilmek yatırımcı için değerli bir yetenek olabilir.
Bu alanda Didier Sornette'in araştırmaları var [1,2], ona göre balonlar fiyat zaman serisindeki artışın üstel artışı (exponential increase) bile geçip süper üstel artış haline gelmesi durumudur. Bu gidişat borsacıların, finansçılar, finans merkezlerinin birbiri ile çok yönlü etkileşimi sonucunda oluşur, ve nihai bir patlama noktası vardır. Sornette modeline deprem tahmin etme amacı ile başlamıştır, ardından aynı yaklaşımı finans balonlarına da uygulayabileceğini farketmiştir.
Model alttaki formüldür:
\[ \ln(p(t)) = A + B(t_c - t)^\beta \big[ 1 + C \cos (\omega \ln(t_c-t) + \phi ) \big] \qquad (1) \]
Türetilmesiyle ilgili detaylar ve referanslar yazının sonunda bulunabilir.
Formülü kullanmak için onu bilinen krizlerden önce elde olan veriye uyduracağız. Normal şartlarda yapılacak budur, bir varlığın, endeksin gidişatının balon olup olmadığı, eğer balon ise ne zaman patlayabileceği merak konusudur. Örnek olarak 1929 ve 1987 krizlerini seçtik.
Ekim 1929 krizi Amerika'da "Büyük Depresyon'' adı verilen dönemin başlangıcıydı, ve kriz öncesi Dow Jones (DJIA) endeksinde müthiş bir artış ardından düşüş gerçekleşti.
import statsmodels.tsa.stattools as st
import pandas as pd, zipfile
with zipfile.ZipFile('data.zip', 'r') as z:
dfj = pd.read_csv(z.open('djia.csv'),index_col='Date',parse_dates=True)
dfs = pd.read_csv(z.open('sp500.csv'),index_col='Date',parse_dates=True)
dfi = pd.read_csv(z.open('ibb.csv'),index_col='Date',parse_dates=True)dfj['Adj Close'].plot()
plt.plot()
plt.savefig('tser_bubble_01.png')
Acaba DJIA bu evrede bir balon muydu? Sornette'in denklemini kriz öncesi veriye uyduralım,
import pandas as pd
from lmfit import Parameters, minimize
from lmfit.printfuncs import report_fit
def init_fit(min, max, init):
fit_params = Parameters()
fit_params.add('tc', value=init, max=max, min=min)
fit_params.add('A', value=2.0, max=10.0, min=0.1)
fit_params.add('m', value=0.5, max=1.0, min=0.01)
fit_params.add('C', value=0.0, max=2.0, min=-2)
fit_params.add('beta', value=0.5, max=1.0, min=0.1)
fit_params.add('omega', value=20., max=40.0, min=0.1)
fit_params.add('phi', value=np.pi, max=2*np.pi, min=0.1)
return fit_params
def f(pars,x):
tc = pars['tc'].value
A = pars['A'].value
m = pars['m'].value
C = pars['C'].value
beta = pars['beta'].value
omega = pars['omega'].value
phi = pars['phi'].value
tmp1 = (1 + C*np.cos(omega*np.log(tc-x) + phi))
model = A - ((m*((tc-x)**beta))*tmp1)
return model
def residual(pars,y,t):
return y-f(pars,t)
fit_params = init_fit(1922.0,1940.,1939)
dfj = dfj[(dfj.index >= '1922-01-01')&(dfj.index <= '1929-01-01')]
dfj['DecDate'] = np.linspace(1922,1929,len(dfj))
y = np.log(dfj['Adj Close'])
t = dfj['DecDate']
out = minimize(residual, fit_params, args=(y,t,))
report_fit(fit_params)[[Variables]]
tc: 1930.26611 +/- 0.060428 (0.00%) (init= 1939)
A: 6.06304875 +/- 0.043302 (0.71%) (init= 2)
m: 0.46154101 +/- 0.027743 (6.01%) (init= 0.5)
C: 0.07785667 +/- 0.003250 (4.17%) (init= 0)
beta: 0.62152034 +/- 0.019028 (3.06%) (init= 0.5)
omega: 10.7292149 +/- 0.176101 (1.64%) (init= 20)
phi: 6.28318123 +/- 6.869443 (109.33%) (init= 3.141593)
[[Correlations]] (unreported correlations are < 0.100)
C(omega, phi) = 0.995
C(m, beta) = -0.994
C(tc, phi) = 0.982
C(tc, omega) = 0.963
C(A, m) = 0.960
C(A, beta) = -0.925
C(m, C) = -0.918
C(A, C) = -0.917
C(C, beta) = 0.903
C(tc, A) = 0.759
C(A, phi) = 0.726
C(A, omega) = 0.697
C(tc, C) = -0.623
C(C, phi) = -0.589
C(C, omega) = -0.559
C(tc, m) = 0.553
C(m, phi) = 0.518
C(m, omega) = 0.489
C(tc, beta) = -0.470
C(beta, phi) = -0.434
C(beta, omega) = -0.404 Formül yılı ondalık yıl (decimal date) formatında istiyor, bu sebeple bazı ek işlemler yapıldı.
Uyumdan gelen sonuç balon patlama anı \(t_c\) olarak 1930 başını verdi. Ve kriz 1929 sonunda gerçekleşti. İyi bir hesap. Dikkat, hesap için 1929 yılının verisini bile almadık ve 1929 sonu 1930 başını elde ettik. Acaba uyum istatiksel olarak ne kadar iyi? Cevap için uyumdan gelen artıklara bakabiliriz, normal regresyonda artıkların gürültü, yani Gaussian dağılıma sahip olmasını kontrol ediyorduk, zaman serisi uyumu için artıkların ortalamaya-dönüşe (mean-reversion) sahip olup olmadığını kontrol edebiliriz. Bunun için ADF testimiz var,
res = list(st.adfuller(out.residual,maxlag=1))
print res[0], '%1,%5,%10', res[4]['1%'], res[4]['5%'], res[4]['10%']-3.94947024619 %1,%5,%10 -3.43409223882 -2.86319299 -2.56765000294Test artıkların yüzde 99 ihtimalle ortalamaya dönüşe sahip olduğunu söylüyor.
Uydurulan fonksiyonu veriyle beraber gösterelim,
dfj['Sornette'] = np.exp(f(fit_params, dfj.DecDate))
dfj[['Adj Close','Sornette']].plot()
plt.savefig('tser_bubble_04.png')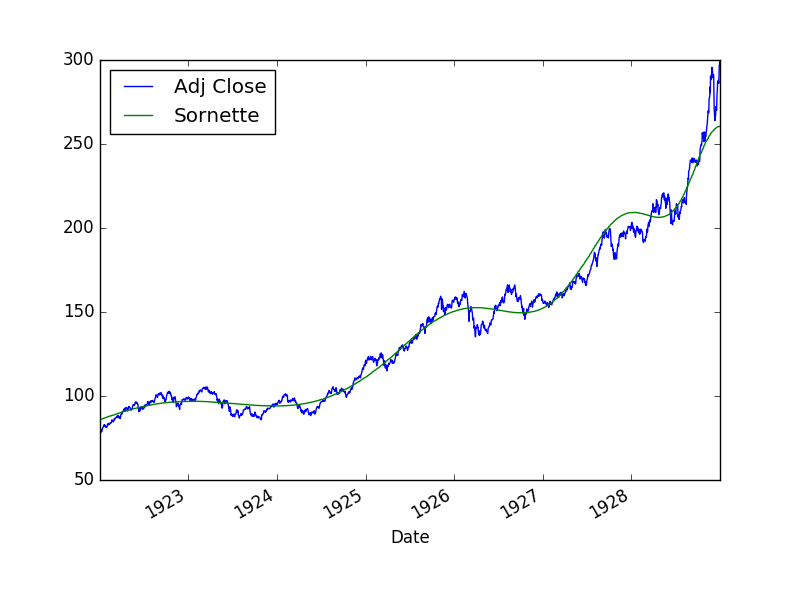
Uyum oldukça iyi. Acaba balon patlama sorusunu daha az veriyle sorsaydık ne olurdu? Yani, acaba, eldeki verinin iki senesini daha silsek, yani aşırı yükselişin olmadığı zamandaki veriyle bir daha hesap yapsak ne cevap alırdık? Modele göre aynı cevabı almamamız gerekir, çünkü formül aşırı çıkışları yakalıyor, ve DJIA'in kriz öncesi son anlarında aşırı çıkış vardı.
fit_params2 = init_fit(1922.0,1940.,1939.)
dfj2 = dfj[:-600] # son iki sene verisini attik
y2 = np.log(dfj2['Adj Close'])
t2 = dfj2['DecDate']
out2 = minimize(residual, fit_params2, args=(y2,t2,))
res2 = list(st.adfuller(out2.residual,maxlag=1))
print res2[0], '%1,%5,%10', res[4]['1%'], res[4]['5%'], res[4]['10%']-2.01491805971 %1,%5,%10 -3.43409223882 -2.86319299 -2.56765000294print fit_params2['tc'].value 1926.91504363Testler yüzde 90 aralığına bile yaklaşamadı. Uyum başarılı değil.
Kara Pazartesi (Black Monday)
Ekim 19, 1987'da S&P 500 büyük bir düşüş yaşadı ve bu gün tarihe Kara Pazartesi olarak geçti. Büyük düşüş öncesi oluşan çıkışın balon olduğu iddia edilmektedir.
dfs['Adj Close'].plot()
plt.savefig('tser_bubble_02.png')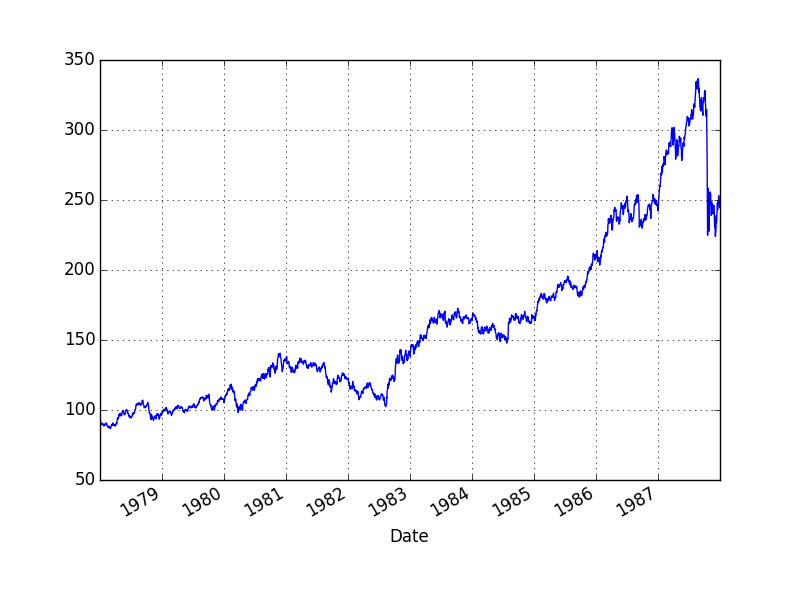
dfs = dfs[(dfs.index < '1987-10-18')] # kara ptesi oncesini al
beg_date = dfs.head(1).index[0].timetuple()
beg_date_dec = beg_date.tm_year + (beg_date.tm_yday / 367.)
end_date = dfs.tail(1).index[0].timetuple()
end_date_dec = end_date.tm_year + (end_date.tm_yday / 367.)
dfs['DecDate'] = np.linspace(beg_date_dec,end_date_dec,len(dfs))
fit_params3 = init_fit(1970.,1995.,1989.)
y3 = np.log(dfs['Adj Close'])
t3 = dfs['DecDate']
out3 = minimize(residual, fit_params3, args=(y3,t3,))
report_fit(fit_params3)[[Variables]]
tc: 1987.78746 +/- 0.001713 (0.00%) (init= 1989)
A: 2.16393842 +/- 0.780555 (36.07%) (init= 2)
m: 0.44165592 +/- 0.757581 (171.53%) (init= 0.5)
C: 0.00092504 +/- 0.121291 (13112.07%) (init= 0)
beta: 0.45100463 +/- 0.517380 (114.72%) (init= 0.5)
omega: 20.2695125 +/- 239.2351 (1180.27%) (init= 20)
phi: 2.80991123 +/- 440.6670 (15682.60%) (init= 3.141593)
[[Correlations]] (unreported correlations are < 0.100)
C(m, beta) = -0.988
C(A, m) = 0.986
C(omega, phi) = -0.958
C(A, beta) = -0.951
C(tc, A) = 0.209
C(tc, m) = 0.206
C(tc, beta) = -0.198
C(C, beta) = 0.117 Cevap kabaca Kara Pazartesi anını yakaladı! Artıkları kontrol edelim,
res3 = list(st.adfuller(out3.residual,maxlag=1))
print res3[0], '%1,%5,%10', res[4]['1%'], res[4]['5%'], res[4]['10%']-2.31790207914 %1,%5,%10 -3.43409223882 -2.86319299 -2.56765000294Tam yüzde 90-95 aralığına düşmedi, fakat çok uzak ta değil. Bu uyumun fena olduğu söylenemez.
Biyoteknoloji
Daha yakın zamandan bir örnek verelim. ABD biyoteknoloji hisselerinde abartılı bir artış olduğu uzun zamandır söylenmekteydi. Biyoteknoloji sektörünü temsil eden bir ETF olan IBB'nin grafiği alttadır.
dfi['Adj Close'].plot()
plt.savefig('tser_bubble_03.png')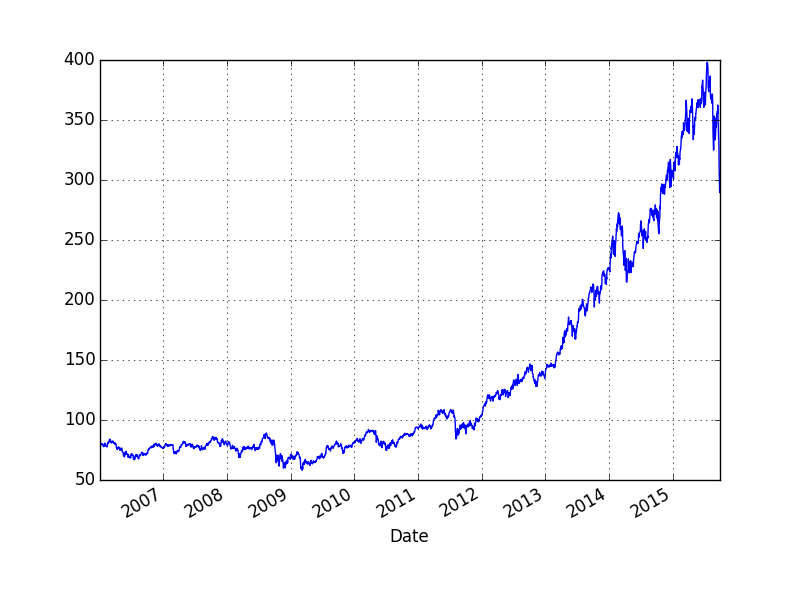
Biyoteknoloji balonu 2015'in ikinci bölümünde patladı ve sert bir düşüş yaşandı. Acaba tekniğimiz bu düşüşü yakalayabilecek mi?
dfi = dfi[(dfi.index < '2015-07-01')]
beg_date = dfi.head(1).index[0].timetuple()
beg_date_dec = beg_date.tm_year + (beg_date.tm_yday / 367.)
end_date = dfi.tail(1).index[0].timetuple()
end_date_dec = end_date.tm_year + (end_date.tm_yday / 367.)
dfi['DecDate'] = np.linspace(beg_date_dec,end_date_dec,len(dfi))
fit_params4 = init_fit(2012.,2018.,2017.)
y4 = np.log(dfi['Adj Close'])
t4 = dfi['DecDate']
out4 = minimize(residual, fit_params4, args=(y4,t4,))
print fit_params4['tc'].value 2015.51052262Sonuç olarak 2015 ortası verildi. Uyum nasıl?
res4 = list(st.adfuller(out4.residual,maxlag=1))
print res4[0], '%1,%5,%10', res[4]['1%'], res[4]['5%'], res[4]['10%']-2.34444994145 %1,%5,%10 -3.43409223882 -2.86319299 -2.56765000294Test sonucu 90-95 aralığına yakın, uyum fena değil.
Bu teknik borsada alım/satım stratejisi bağlamında otomize olarak kullanılabilir, ya da belli bazı hisselerden ne zaman uzak durulacağı konusunda bir alarm vermek için faydalı olabilir.
Türetmek
Sornette'in modelinin başlangıcı bir zaman serisindeki artışının üstel (exponential) hızı geçtiği zaman sonlu-anda (finite-time) bir eşsizlik (singularity) çıktığı iddiası [1,4]. Eşsizlik konusunu {} notlarında işledik; eşsiz nokta bir fonksiyonun analitikliği kaybettiği yerdir. Peki modelde eşsizliğin ortaya çıkması gerçek hayatta illa bunun olacağı anlamına geliyor mu? İlginç bir şekilde eğer matematiksel model sağlam ise eşsizliğin tahmin edildiği yerde hakikaten bu durum ortaya çıkıyor, mesela izafiyet kuramının matematiği eşsiz noktaların varlığını tahmin eder, ve hakikaten de tahmin edildiği şekilde uzayda bu noktalarda kara deliklerin olduğu ispatlanmıştır. Aynı şekilde bir materyelin kırılması / parçalanması matematiksel modelin eşsizlik noktasında olur, ve deneylerde bu anda materyel kırılması gözlenmiştir.
Sornette'e göre nüfus artışı, bir ekonominin ürettiği değeri temsil eden gayrısafi yurtiçi hasıla (gross domestic product -GDP-) artışı rakamlarına dünya bazında bakarsak üstel üstü artışları görebiliyoruz, ve aynen materyel kırılmasında olduğu gibi modelin eşsizlik tahmin ettiği yeri "bir fazın bittiği an'' olarak görürsek, bu nokta bir tür sürdüremezliğin geldiği an olacaktır, ve tabiri caizse "inceldiği yerden kopma'' noktasıdır, ve bunun ötesinde mesela ne daha fazla nüfus artışı, ne de ekonomik büyüme mümkün değildir. En azından mevcut çevre, mevcut ölçümler üzerinden ekonomik büyüme dediğimiz şey olmayacaktır.
Sonlu an eşsizliğine erişmek için mesela normal nüfus artışı modelinden başlayalım, nüfusu modellemenin en iyi bilinen yolu Lojistik Denklemdir, bkz [6], [7], [8]. Model şöyledir;
\[ \frac{dp}{dt} = rp(t) [ K - p(t) ] \]
Lojistik modelde bir taşıma kapasitesi \(K\) vardır, ve bu kapasitenin daha fazlasını çevre koşullarının taşıması mümkün değildir. Fakat [4]'teki referanslara göre şu iddia edilmektedir; \(p(t)\) ile birlikte \(K\) de artmaktadır, çünkü araçlarımızı daha iyi kullanıyoruz, sürekli keşifler yapıyoruz, ilaçlar, gübre çeşitleri, vs. ve yeni bölgelere yayılıyoruz, yani sürekli taşıma kapasitesini aşıyoruz. Bu durumda, yani \(K > p(t)\)'in olduğu durumda lojistik denklemini çözümü patlar, yani uzaklaşır (divergent) hale gelir ve sonsuza gider. Bu gidiş süresi, eşsizlik öncesi varışta giden zaman sonludur, yani belli bir büyüklüğü vardır.
Bu durumda denkleme artık hiçbir etkisi olmayan \(-p(t)\) denklemden çıkartılabilir, ve o zaman geri kalanlar \(\delta > 1\) olacak şekilde \(K \propto p^{1+\delta}\) kabul edilebilir, yani \(K\)'nin kendisi \(p\)'ye oranla büyüyor ve arada bir üstel kanun (power law) ilişkisi vardır. Şimdi aynı formülü şu şekilde yazarız,
\[ \frac{dp}{dt} = r [p(t)]^{1+\delta} \]
ki bu formüle göre artış oranı \(r [p(t)]^{1+\delta}\) olarak hızlanmaktadır. Çözelim,
\[ \int \frac{dp}{p(t)^{1+\delta}} = \int rt\]
\[ \int p(t)^{-1-\delta} \mathrm{d} p = rt + C \]
\(t_c\)'ye (ki bir sabit) erişmek amaçlı olarak \(C = -rt_c\) tanımlayalım,
\[ \frac{p(t)^{-\delta}}{-\delta} = rt - rt_c \]
\[ p(t)^{-\delta}= -\delta r(t - t_c) \]
\(t-t_c = -(t_c-t)\) olduğu için parantez içindeki çıkartma işlemi şu hale gelir,
\[ p(t)^{-\delta}= \delta r(t_c - t) \]
İstediğimiz forma yaklaştık çünkü \(t_c\)'yi eşsizlik anı olarak hesaplamak istiyoruz, ve \(t\) bu andan önceki zamanı temsil ediyor olmalı. Şimdi \(\alpha = -\frac{1}{\delta}\) tanımlayalım, ve eşitliğin her iki tarafının \(\alpha\) üstünü alalım,
\[ (p(t)^{-\delta})^\alpha= (\delta r )^\alpha (t_c - t)^\alpha \]
Eğer \(p(0) = p_0 = (\delta r )^\alpha\) kabul edersek, eşitliğin sol tarafını basitleştirince,
\[ p(t) = p_0 (t_c - t)^\alpha \]
elde ederiz, ki bu denklemin \(t_c\) anında eşsizliği vardır.
Şimdi bu basit modeli veri üzerinde test edelim. Elimizde bir milyon yıl geriye giden nüfus modeli var [3], sadece 0'inci yıl ile 1989 arasını alalım, ve modeli uyduralım ve bilinmeyen parametreleri hesaplamaya uğraşalım. Veriyi uydurma amaçlı olarak şu formül daha kullanışlı olabilir,
\[ p(t) = A + B(t_c - t)^z \qquad (2) \]
import pandas as pd
dfpop = pd.read_csv('wpop.csv',comment='#',sep='\s')
dfpop = dfpop[(dfpop['Year'] >= 0) & (dfpop['Year'] <= 1998)]import pandas as pd
import statsmodels.tsa.stattools as st
from lmfit import Parameters, minimize
from lmfit.printfuncs import report_fit
def f(pars,t):
tc = pars['tc'].value
z = pars['z'].value
A = pars['A'].value
B = pars['B'].value
model = A + B*((tc - t)**z)
return model
def residual(pars,y,t):
return y-f(pars,t)fit_params = Parameters()
fit_params.add('tc', value=2100.0, min=2000.,max=2400.)
fit_params.add('z', value=-1., min=-5.0,max=5.0)
fit_params.add('A', value=0., min=0.0, max=10.0)
fit_params.add('B', value=20*1000., min=0.0,max=30*1000.0)
y = np.log(np.array(dfpop.Population.astype(float)))
t = np.array(dfpop.Year.astype(float))
out = minimize(residual, fit_params, args=(y,t,))
report_fit(fit_params)
res = list(st.adfuller(out.residual,maxlag=1))
print 'ADF testi', res[0], '%1,%5,%10', res[4]['1%'], res[4]['5%'], res[4]['10%'][[Variables]]
tc: 2047.37659 +/- 10.86346 (0.53%) (init= 2100)
z: -0.24662286 +/- 0.062236 (25.24%) (init=-1)
A: 2.72771567 +/- 0.669841 (24.56%) (init= 0)
B: 15.9169748 +/- 2.943371 (18.49%) (init= 20000)
[[Correlations]] (unreported correlations are < 0.100)
C(z, A) = -0.996
C(z, B) = -0.992
C(tc, B) = 0.981
C(A, B) = 0.977
C(tc, z) = -0.954
C(tc, A) = 0.926
ADF testi -3.14127355675 %1,%5,%10 -3.61550910118 -2.94126235749 -2.60919950139Sonuç +- 10 sene hata payı ile 2047 senesi çıktı. Artıklar üzerinde ADF testi yaptık, yüzde 95 kesinliğinde artıkların ortalamaya dönüş özelliğine sahip olduğunu görüyoruz. Model uyumu iyi demek.
GDP verisine bakalım,
import pandas as pd
dfgdp = pd.read_csv('wgdpreal.csv',comment='#',sep='\s')
dfgdp = dfgdp[(dfgdp['Year'] >= 0) & (dfgdp['Year'] <= 1998)]fit_params = Parameters()
fit_params.add('tc', value=2100.0, min=2000.,max=2400.)
fit_params.add('z', value=-1., min=-5.0,max=5.0)
fit_params.add('A', value=0., min=0.0, max=10.0)
fit_params.add('B', value=20*1000., min=0.0,max=30*1000.0)
y = np.log(np.array(dfgdp.GDPPC.astype(float)))
t = np.array(dfgdp.Year.astype(float))
out = minimize(residual, fit_params, args=(y,t,))
report_fit(fit_params)
res = list(st.adfuller(out.residual,maxlag=1))
print 'ADF testi', res[0], '%1-%10', res[4]['1%'], res[4]['5%'], res[4]['10%'][[Variables]]
tc: 2148.16544 +/- 21.95284 (1.02%) (init= 2100)
z: -1.33135253 +/- 0.155306 (11.67%) (init=-1)
A: 2.81936402 +/- 0.092028 (3.26%) (init= 0)
B: 6344.88666 +/- 5.51e+03 (86.76%) (init= 20000)
[[Correlations]] (unreported correlations are < 0.100)
C(z, B) = -0.999
C(tc, B) = 0.987
C(tc, z) = -0.981
C(z, A) = -0.928
C(A, B) = 0.917
C(tc, A) = 0.861
ADF testi -2.65894249385 %1-%10 -3.61550910118 -2.94126235749 -2.60919950139Burada +- 20 sene hata payıyla 2148 çıktı (daha var!), artıklar yine ortalama dönüşe sahip. Bu demektir ki ekonomik büyüme, mevcut gidişatıyla patlama yapacaktır ve kritik an bir tür faz sonu (end of a regime) olarak addedilebilecektir. Mevcut şartlar altında bundan daha fazlası mümkün değil.
Log Salınım (Log Oscillation)
[4,5]'te bu modelin geliştirilerek (1) formülüne nasıl erişildiğinin detayları bulunabilir. Hikayenin özü şöyle; materyel kırılması ve buna benzer diğer doğal olaylarda eşsizlik anı öncesi log salınımlar olduğu da görülmüştür. Bu salınımlara matematiksel olarak erişmek için (2)'deki formüldeki \(z\) üstelinin kompleks sayı olmasına izin verilir, yani \(\beta + i\omega\) formunda olduğu farz edilir, ve bu şekilde türetime devam edince ortaya (1)'deki log periyodik salınımlar çıkar. Detaylar için [1,4]. Sornette bu salınım ekinin formülü "dekore'' ettiğini söylemektedir, güzel bir kelime seçilmiş, hakikaten bu salınımlar ana formüle bir ek, onu "süslüyor'', fakat tabii ki bu sayede eşsizlik noktasını yakalamamız kolaylaşıyor çünkü uydurma rutinimiz artık verideki bu salınımları da veride bulmaya uğraşıyor böylece aradığı tüm parametrelerin kalitesi artmış oluyor.
Sornette bazı kaynaklarda bir değişik türetim şekli daha uyguluyor [1,5]; buna göre \(p(t)\) olarak belirttiğimiz \(h(t)\), tehlike oranı (hazard rate) olarak modellenir, ve fiyat serisi \(p(t)\) olarak rasgele calculus'tan gelinerek modelleniyor, ve \(h(t)\), \(p(t)\)'ye sokuluyor, ve ortaya log salınımlı model çıkıyor. Bu türetişin bazı ilginç bağlantıları var, mesela tehlike oranının kimi aşırı, kimi az ama hepsi birbiriyle etkileşimde olan borsacıların birbirini taklit etmesi yüzünden \(h(t)\)'nin arttığı modellenmekte, ki bu artış ta bir üstel kanunu takip ediyor. Fizik ve sosyal modelde birbiri ile aşırı etkileşim sürekli ortaya üstel kanun çıkartıyor, bunu biliyoruz. Patlama anı ve öncesinde aslında ortada olan bir kaos değil, kaos yokluğu. Bütüne bakıldığında biri rasgele bazen satan, biri rasgele bazen alan borsacıların patlama anı öncesi birdenbire düzenli bir şekilde hepsi satıyor.
Kaynaklar
[1] Sornette, Why Stock Markets Crash
[2] Sornette, How we can predict the next financial crisis, https://www.youtube.com/watch?v=C_eFjLZqXt8
[3] Long, Estimates of World GDP, One Million B.C. - Present
[4] Sornette, Finite-time singularity in the dynamics of the world population, economic and financial indices
[5] Geraskin, Everything You Always Wanted to Know about Log Periodic Power Laws for Bubble Modelling but Were Afraid to Ask
[6] Bayramlı, Diferansiyel Denklemler, Matematiksel Modelleme
[7] Bayramlı, Gayrı Lineer Dinamik ve Kaos, Ders 1
[8] Bayramlı, Diferansiyel Denklemler, Ders 5