Diyelim ki bir video kameradan gelen imajları kullanarak obje takip eden bir yazılım istiyoruz. Matematiksel olarak obje nedir? İmajı nedir? obje kendi dünyasında bir süreci takip etmektedir, 3 boyutlu uzayda bir yer kaplamaktadır ve orada hareket etmektedir. Biz bu hareketi belli bir güven aralığı / hata payı üzerinden biliyor olabiliriz. Diğer yandan objenin kameraya yansıttığı imaj vardır, bu imaj 2 boyutlu ve kameranın özellikleriyle alakalı parametreler sebebiyle belli bir şekilde “yansıtılmış (project)’’ olacaktır. Biz bu yansıtma formülünü de, belli bir hata payı üzerinden, biliyor olabiliriz.
Bu durumu şöyle modelleyebiliriz,
\[ x_k = \Phi_{k-1}x_{k-1} + w_{k-1} \]
\[ z_k = H_k x_k + v_k \]
\(x_k = (n \times 1)\) vektörü, \(k\) anındaki sürecin durumu (state)
\(\Phi_k = (n \times n)\) matrisi, \(x_{k-1}\) durumundan \(x_{k}\) durumuna geçişi tarif eden formül.
\(w_k = (n \times 1)\) vektörü, sıfır ortalamalı, kovaryansı \(Q_k\) olan beyaz gürültü.
\(z_k = (n \times 1)\) vektörü, dışarıdan alınan ölçüm.
\(H_k = (m \times n)\) matrisi, gizli konum bilgisinin dışarıya nasıl ölçüm olarak yansıdığının formülü. Bu dönüşüm ideal, yani gürültüsüz durumu tarif eder.
\(v_k = (m \times 1)\) vektörü, ölçüm hatası.
Yani formüllerin söylediği şudur: ilk formül bize izlenen her ne ise onun hareketini tarif ediyor, \(k-1\) anından \(k\) anına geçişini tarif ediyor. \(z_k\) ise bu \(x_k\)’nin dışarıdan alınan ölçümü. Bizim yapmak istediğimiz \(z_k\)’leri kullanarak \(x_k\)’nin nerede olduğunu kestirebilmek.
Sıfır merkezli gürültü şu demektir,
\[ E[v_k] = E[w_k] = 0 \]
Ayrıca,
\[ E[v_kv_k^T] = R_k \]
\[ E[w_kw_k^T] = Q_k \]
Kalman filtreleri (KF) ile yapmak istediğimizin dışarıdan görünen \(z_k\)’yi kullanarak gizli \(x_k\)’yi kestirmek olduğunu söylemiştik. Ayrıca bu tahminleri her gelen veri noktasına göre sürekli güncelliyor olacağız, yani 100 tane veri noktasını almak için bekleyip sonra toptan bir analiz yapmaya gerek yok (istenirse yöntem toptan işleyecek şekilde de kullanılabilir tabii). Tahmin edilebileceği üzere bu tür bir gerçek zamanlı kabiliyetin pek çok mühendislik uygulaması olabilir; hakikaten de mesella aya ilk insanlı ınışı yapan Apollo modülü bir Kalman filtresi kullanıyordu.
KF’i türetmek için önce bir lineer tahmin edici (estimator) tanımlamak gerekir, ve sonra bu tahmin ediciyi optimize eden şartların ne olduğu incelenir. Şu notasyonu kullanalım: Tilde yani \(\tilde{x}\) üzerindeki işaret, o değişkenin tahmin ile gerçeği arasındaki hatayı temsil etmesi içindir, \(\hat{x}\) üzerindeki şapka ise istatistik dersinden hatırlayacağımız üzere tahmin edici (estimator). Ayrıca bir değişkenin üzerindeki \(^-\) ve \(^+\) işaretlerini bu değişkenin ölçüm dikkate alındıktan önceki ve sonraki (o sırayla) hali olarak tanımlayalım.
Konum bilgisi ve hata arasındaki ilişkiyi şu şekilde belirtelim,
\[ \hat{x}_k^+ = x_k + \tilde{x_k}^+ \]
\[ \hat{x}_k^- = x_k + \tilde{x_k}^- \]
Elimizdeki en iyi tahmin \(\hat{x}_k^-\)’i yeni veri / ölçüm elde ettikten sonra güncellemek istiyoruz. Bunu yaparken gürültülü ölçümle eldeki en son tahmini lineer bir şekilde birleştirmek istiyoruz. Bu birleştirmeyi,
\[ \hat{x}_k^+ = \hat{x}_k^- + K_k (z_k - H_k \hat{x}_k^-) \]
olarak temsil edebiliriz, \(\hat{x}_k^+\) güncellenmiş tahmindir, \(K_k\) ise birleştirme faktörüdür (blending factor), ki bu değerin ne olduğunu şu anda bilmiyoruz.
Tekrar düzenlersek,
\[= \hat{x}_k^- - K_kH_k\hat{x}_k^- + K_kz_k \]
\[ \hat{x}_k^+ = \hat{x}_k^- (I - K_kH_k) + K_kz_k \]
Daha temiz olması için \(K_k' = I - K_kH_k\) diyelim, ve en baştaki formülleri bir daha alta alta yazalım,
\[ \hat{x}_k^+ = K_k' \hat{x}_k^- + K_kz_k \qquad (1) \]
\[ z_k = H_k x_k + v_k \qquad (2) \]
\[ \hat{x}_k^+ = x_k + \tilde{x_k}^+ \qquad (3) \]
\[ \hat{x}_k^- = x_k + \tilde{x_k}^- \qquad (4) \]
\[ \hat{x}_k^+ = K_k' \hat{x}_k^- + K_k(H_k x_k + v_k) \]
Eşitliğin solunu (3) ile açalım,
\[ x_k + \tilde{x_k}^+ = K_k' \hat{x}_k^- + K_k(H_k x_k + v_k) \]
ve \(x_k\)’yi sağa geçirelim,
\[ \tilde{x_k}^+ = K_k' \hat{x}_k^- + K_k(H_k x_k + v_k) - x_k \]
\(\hat{x}_k^-\) yerine (4)
\[ = K_k' (x_k + \tilde{x_k}^-) + K_k(H_k x_k + v_k) - x_k \]
\(x_k\)’leri yanyana getirip gruplayalım,
\[ = K_k' x_k + K_kH_k x_k - x_k + K_k'\tilde{x_k}^- + K_kv_k \]
\[ \tilde{x_k}^+ = x_k (K_k' + K_kH_k - I) + K_k'\tilde{x_k}^- + K_kv_k \]
Üstteki tüm ifadenin beklentisini aldığımız zaman,
\[ E[\tilde{x_k}^+] = E[x_k (K_k' + K_kH_k - I)] + E[K_k'\tilde{x_k}^-] + E[K_kv_k] \]
olacak değil mi? Burada biraz duralım, ve yansızlık kavramını düşünelim. Eğer tahmin edici \(\hat{x}^+\) yansız (unbiased) olsun istiyorsak, bu şu anlama gelir,
\[ E[\hat{x_k}^+] = E[x_k] \]
Düzenleyelim,
\[ E[\hat{x_k}^+] - E[x_k] = 0\]
\[ E[\hat{x_k}^+ - x_k] = 0\]
\[ E[ \tilde{x_k}^+] = 0\]
Şimdi, formülü son bıraktığımız yere dönelim, orada eğer \(E[\tilde{x_k}^+]=0\) olsun istiyorsak ve \(E[\tilde{x_k}^-] = 0\)’in da doğru olduğu durumda geriye tek kalan \(K_k' + K_kH_k - I\) ifadesinin sıfır olmasıdır (çünkü \(E[v_k]=0\) olacak zaten), bu durumda herhangi bir \(x_k\) için beklentinin sıfır gelmesi
\[ K_k' + K_kH_k - I = 0 \]
olmasına bağlıdır. Tabii o doğru ise,
\[ K_k' = I - K_kH_k \]
Bu ifadeyi geriye, (1)’deki tahmin edicinin içine koyarsak
\[ \hat{x}_k^+ = (I - K_kH_k ) \hat{x}_k^- + K_kz_k \]
Ya da
\[ \hat{x}_k^+ = \hat{x}_k^- + K_k(z_k - H_k\hat{x}_k^- ) \]
Eğer \(\hat{x}_k^-\) için (4) kullanırsak,
\[ \hat{x}_k^+ = (x_k + \tilde{x_k}^-) + K_k(z_k - H_k( x_k + \tilde{x_k}^-) ) \]
Tekrar gruplama,
\[ \hat{x}_k^+ = \tilde{x_k}^- (I - K_kH_k) + x_k + K_k(z_k - H_kx_k) \]
Ve (2)’yi \(z_k - H_kx_k\) için kullanalım,
\[ \hat{x}_k^+ - x_k = (I - K_kH_k)\tilde{x_k}^- + K_kv_k \]
\[ \tilde{x}_k^+ = (I - K_kH_k)\tilde{x_k}^- + K_kv_k \]
Böylece tekabül eden tahmin hatasını hesaplamış olduk.
Tanım
\[ P_k^+ = E[ \tilde{x_k}^+\tilde{x_k}^{+T} ]\]
\[ P_k^- = E[ \tilde{x_k}^- \tilde{x_k}^{-T} ]\]
Bu kovaryans hesabının uygulanmasından ibaret aslında. Şimdi üç üstteki formülü üstten ikincisine sokarsak,
\[ = E \big[ (I - K_kH_k)\tilde{x_k}^- + K_kv_k \big] \big[\tilde{x_k}^{-T}(I - H_k^TK_k^T) + v_k^TK_k^T \big] \]
Yani
\[ = E \bigg[ (I - K_kH_k)\tilde{x_k}^- \big( \tilde{x_k}^{-T}(I - H_k^TK_k^T) + v_k^TK_k^T \big) + \qquad (5) \]
\[ K_kv_k \big( \tilde{x_k}^{-T}(I - H_k^TK_k^T) + v_k^TK_k^T \big) \bigg] \]
Önceden tanımlamıştık,
\[ P_k^- = E[ \tilde{x_k}^- \tilde{x_k}^{-T} ]\]
\[ E[v_kv_k^T] = R_k \]
Ayrıca ölçüm hataları ve gürültü arasında korelasyon olmadığını farz ettiğimiz için,
\[ E[\tilde{x_k}^-v_k^T] = E[v_k\tilde{x_k}^{-T}] = 0 \]
Tüm bunları (5)’i basitleştirmek için kullanırsak,
\[ P_k^{+} = (I - K_kH_k)P_k^-(I - H_k^TK_k^T) + K_kR_kK_k^T \qquad (6) \]
En optimal \(K_k\)’yi nasıl buluruz? Amaç \(P_k^+\) matrisinin çaprazındaki değerleri minimize etmektir, bu durumda optimize etmek istediğimiz bedel (cost) fonksiyonu
\[ J_k = E[ \tilde{x_k}^{+T}\tilde{x_k} ] \]
olsun, ki bu tek bir sayısal değer verir. Bu aslında
\[ J_k = Tr(P_k^+) \]
değerinin optimize edilmesi ile aynı şeydir. Değil mi? Ya iki üstteki gibi vektör uzunluğunu minimize ediyoruz, ya da kovaryansın çaprazının izini (trace) minimize ediyoruz, çünkü her ikisinde de aynı değerler var. İz operatörü hatırlayacağımız üzere bir matrisin çaprazındaki değerleri toplar. İz kullanmamızın sebebi bize bazı türevsel numaralar sağlaması,
Biliyoruz ki, eger \(B\) simetrik ise,
\[ \frac{\partial }{\partial A} Tr(ABA^T) = 2AB \]
\[ Tr(P_k^{+}) = Tr((I - K_kH_k)P_k^-(I - H_k^TK_k^T)) + Tr(K_kR_kK_k^T) \]
İki tane iz var, bu izler içinde bir \(ABA^T\) formu görebiliyoruz herhalde, onların \(K_k\)’ye göre türevini alıyoruz,
\[ \frac{\partial Tr(P_k^{+})}{\partial K_k} = -2(I - K_kH_k)P_k^- H_k^T + 2K_kR_k \]
Şimdi sıfıra eşitleyip \(K_k\) için çözelim,
\[ 0 = -2(I - K_kH_k)P_k^- H_k^T + 2K_kR_k \]
\[ 2P_k^- H_k^T = 2K_kH_kP_k^- H_k^T + 2K_kR_k \]
\[ P_k^- H_k^T = K_kH_kP_k^- H_k^T + K_kR_k \]
\[ P_k^- H_k^T = K_k(H_kP_k^- H_k^T + R_k) \]
\[ K_k = P_k^- H_k^T(H_kP_k^- H_k^T + R_k)^{-1} \]
\(K_k\) matrisine Kalman kazanç matrisi (Kalman gain matrix) ismi de verilir. Ve en son olarak bu sonucu (6) içine koyarsak, ve biraz manipülasyon ardından,
\[ P_k^+ = P_k^- -P_k^- H_k^T (H_kP_k^- H_k^T + R_k)^{-1}H_kP_k^- \]
\[ = [I - K_kH_k]P_k^- \]
sonucunu elde ederiz.
Bu hesaplar ölçüm aldıktan sonra tahmini güncellemek içindi. Peki ölçüm almadan önceki tahmini nasıl yaparız? Bunu yapmamız gerekir çünkü ölçüm gelmeden önce yeni bir tahmin yapılmalı ki o tahmini, onun hatasını bir sonraki ölçüm ile düzeltilebilelim. Bu geçişin nasıl olacağını en başta belirttiğimiz KF modeli gösteriyor zaten, konum geçişi / adımı ona göre atıp, sonucun beklentisini ve kovaryansını hesaplıyoruz,
\[ \hat{x}_k^- = E[\Phi_{k-1}x_{k-1}^+ + w] = \Phi_{k-1}x_{k-1}^+ \]
\[ P_k^- = Cov(\Phi_{k-1}x_{k-1}^+) = E[(\Phi_{k-1}x_{k-1}^+ + w)(\Phi_{k-1}x_{k-1}^+ + w)^T) \]
\[ = \Phi_{k-1}P_{k-1}^+\Phi_{k-1}^T + Q_{k-1} \]
\(P_k^-\) hesabında ne olduğuna dikkat, bir sonraki ölçüm olmadan sadece geçiş formülü üzerinde tahmin etmeye uğraştık, ve bu tabii ki bilinmezliği arttırdı (\(Q\) toplanıyor).
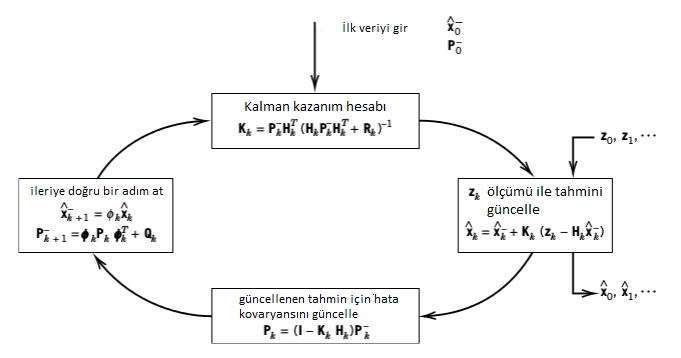
En son adım bu; \(\hat{x}_k^-,P_k^-\) artık bir sonraki güncelleme için kullanılacak değerlerdir. Bu noktada başa dönüyoruz, ve aynı işlemleri tekrarlıyoruz. Eğer verinin alımı, model güncellemesi, ileri tahmin adımında olanları bir figürle göstermek gerekirse (indisler resimde bir ileri alınmış, bunu aklımızda düzelterek bakalım),

Aslında tüm bu süreci bir sözde kod (pseudocode) parçası ile
göstermeyi düşünmüştük, ki ölçüm verisi bir for döngüsü ile
listeden alınarak teker teker işlenecekti, fakat bu üstteki tarifi tam
anlatamayacaktı, çünkü KF için illa elde belli sayıda “işlenip
bitirilen’’ ölçüm olması gerekmez. Güncelleme her yeni ölçüm için, o tek
ölçüm bazında yapılabildiği için şimdi 1 tane, sonra 10 tane, sonra
bekleyip 2 tane daha, vs. şeklinde veri işlenmesi gayet mümkündür. Bu
işlem gerçek zamanlı olabilir, ya da bir listeyi gezerek anlık olmayan
bir şekilde olabilir. Bu yüzden üstteki döngü resmini tercih ettik.
Not: Bazı kaynaklarda Kalman Filtrelerinin uygun bir model üzerinden en az kareler (least square) ile yani çizgi / düzlem uydurması ile aynı sonuca varabileceği söylenir, bu tam doğru degil, KF üstel ağırlıklı (exponentially weighted) en az kareler ile aynıdır, yani en son veri noktalarının daha öncekilere göre daha çok ağırlığı vardır. KF ile regresyon örneği için bkz [5] yazısı.
Bir not daha: \(x_k = \Phi_{k-1}x_{k-1} + w_{k-1}\) geçişinde \(\Phi_{k-1}\) ile çarpım bir lineer konum değişimini modeller, o zaman lineer olmayan geçişlerin KF modellenmesi mümkün değildir. Mesela bir topun ileri, havaya doğru atıldığı bir örneği düşünelim, ölçümlerde Gaussian gürültü olsun. Topun gidişi bir parabolu takip edecektir, oldukca basit bir gidiştir, fakat KF’in bu gidişi takip etmesi mümkün değildir. Parçacık filtreleri, genişletilmiş KF (EKF), UKF gibi yaklaşımlar bu sebeple alternatif haline gelmişlerdir.
Bir KF kodlaması alttadır.
from numpy import *
# x_{t+1} = Phi x_t + Sigma_x
# y_t = Hx_t + R
class Kalman:
# T is the translation matrix
# K is the camera matrix calculated by calibration
def __init__(self, K, mu_init):
self.ndim = 3
self.Sigma_x = eye(self.ndim+1)*150
self.Phi = eye(4)
self.Phi[2,3] = -0.5
self.H = append(K, [[0], [0], [0]], axis=1)
self.mu_hat = mu_init
self.cov = eye(self.ndim+1)
self.R = eye(self.ndim)*1.5
def normalize_2d(self, x):
return array([x[0]/x[2], x[1]/x[2], 1.0])
def update(self, obs):
# Make prediction
self.mu_hat_est = dot(self.Phi,self.mu_hat)
prod = dot(self.Phi, dot(self.cov, transpose(self.Phi)))
self.cov_est = prod + self.Sigma_x
# Update estimate
prod = self.normalize_2d(dot(self.H,self.mu_hat_est))
self.error_mu = obs - prod
prod = dot(self.cov,transpose(self.H))
prod = dot(self.H,prod)
self.error_cov = prod + self.R
prod = dot(self.cov_est,transpose(self.H))
self.K = dot(prod,linalg.inv(self.error_cov))
self.mu_hat = self.mu_hat_est + dot(self.K,self.error_mu)
prod = dot(self.K,self.H)
left = eye(self.ndim+1)
diff = left - prod
self.cov = dot(diff, self.cov_est)Örnek
Diyelim ki tek boyutta bir köpeğin gidişini modellemek istiyoruz [4, pg. 191]. Köpek sabit bir hızda ilerliyor olsun (bu geçiş modeli), ve biz onu sadece havlamaların nereden geldiği ile bulmaya uğraşacağız (bu da gürültülü ölçüm). Geçiş
\[ x = v \Delta t + x_0\]
Hız \(v\) yerine \(\dot{x}\) kullanalım, o zaman
\[\bar x = x + \dot x \Delta t\]
Hız sabit olacağı için onun geçişi şöyle,
\[\bar{\dot x} = \dot x\]
Alt alta yazalım,
\[\begin{cases} \begin{aligned} \bar x &= x + \dot x \Delta t \\ \bar{\dot x} &= \dot x \end{aligned} \end{cases}\]
Düzenlersek,
\[\begin{cases} \begin{aligned} \bar x &= 1x + &\Delta t\, \dot x \\ \bar{\dot x} &=0x + &1\, \dot x \end{aligned} \end{cases}\]
Matris formunda
\[\begin{aligned} \begin{bmatrix}\bar x \\ \bar{\dot x}\end{bmatrix} &= \begin{bmatrix}1&\Delta t \\ 0&1\end{bmatrix} \begin{bmatrix}x \\ \dot x\end{bmatrix}\\ \end{aligned}\]
\[ \mathbf{\bar x} = \mathbf{Fx} \]
Yani konumu iki boyutlu olarak modellemiş olduk.
\[\mathbf x =\begin{bmatrix}x \\ \dot x\end{bmatrix}\]
Peki ölçüm tahminlerini üretecek \(H\) nasıl olmalı?
\[\mathbf H=\begin{bmatrix}1&0\end{bmatrix}\]
Bunu yaptık çünkü \(Hx\) çarpımı yapılınca sadece \(x\) çarpıma girecek, hız sıfırlanacak, yani ölçümde kullanılmayacak. Bu tam istediğimiz şey zaten. Ne kadar ilginç değil mi? Hız konumda yer alan bir şey, tahmin / ölçüm / düzeltme döngüsü sırasında KF onu da değiştirecek, düzeltecek, ölçümde kullanılmıyor olsa bile!
Ölçümdeki belirsizliğe 10 metre diyelim,
\(R = \begin{bmatrix}10\end{bmatrix}\)
Altta alternatif bir KF kodu ve örneğin kodlamasını görüyoruz,
from scipy.stats import norm, multivariate_normal
import pandas as pd, math
import numpy as np, numpy.linalg as linalg
import matplotlib.pyplot as plt
def logpdf(x, mean, cov):
flat_mean = np.asarray(mean).flatten()
flat_x = np.asarray(x).flatten()
return multivariate_normal.logpdf(flat_x, flat_mean, cov, True)
def dot3(A,B,C):
return np.dot(A, np.dot(B,C))
def setter_scalar(value, dim_x):
if np.isscalar(value):
v = np.eye(dim_x) * value
else:
v = np.array(value, dtype=float)
dim_x = v.shape[0]
if v.shape != (dim_x, dim_x):
raise Exception('must have shape ({},{})'.format(dim_x, dim_x))
return v
def setter(value, dim_x, dim_y):
v = np.array(value, dtype=float)
if v.shape != (dim_x, dim_y):
raise Exception('must have shape ({},{})'.format(dim_x, dim_y))
return v
def setter_1d(value, dim_x):
v = np.array(value, dtype=float)
shape = v.shape
if shape[0] != (dim_x) or v.ndim > 2 or (v.ndim==2 and shape[1] != 1):
raise Exception('has shape {}, must have shape ({},{})'.format(shape, dim_x, 1))
return v
def Q_discrete_white_noise(dim, dt=1., var=1.):
assert dim == 2 or dim == 3
if dim == 2:
Q = np.array([[.25*dt**4, .5*dt**3],
[ .5*dt**3, dt**2]], dtype=float)
else:
Q = np.array([[.25*dt**4, .5*dt**3, .5*dt**2],
[ .5*dt**3, dt**2, dt],
[ .5*dt**2, dt, 1]], dtype=float)
return Q * var
class KalmanFilter(object):
def __init__(self, dim_x, dim_z, dim_u=0):
assert dim_x > 0
assert dim_z > 0
assert dim_u >= 0
self.dim_x = dim_x
self.dim_z = dim_z
self.dim_u = dim_u
self._x = np.zeros((dim_x,1)) # state
self._P = np.eye(dim_x) # uncertainty covariance
self._Q = np.eye(dim_x) # process uncertainty
self._B = 0 # control transition matrix
self._F = 0 # state transition matrix
self.H = 0 # Measurement function
self.R = np.eye(dim_z) # state uncertainty
self._alpha_sq = 1. # fading memory control
self.M = 0 # process-measurement cross correlation
# gain and residual are computed during the innovation step. We
# save them so that in case you want to inspect them for various
# purposes
self._K = 0 # kalman gain
self._y = np.zeros((dim_z, 1))
self._S = np.zeros((dim_z, dim_z)) # system uncertainty
# identity matrix. Do not alter this.
self._I = np.eye(dim_x)
def update(self, z, R=None, H=None):
if z is None:
return
if R is None:
R = self.R
elif isscalar(R):
R = eye(self.dim_z) * R
# rename for readability and a tiny extra bit of speed
if H is None:
H = self.H
P = self._P
x = self._x
# handle special case: if z is in form [[z]] but x is not a column
# vector dimensions will not match
if x.ndim==1 and np.shape(z) == (1,1):
z = z[0]
if np.shape(z) == (): # is it scalar, e.g. z=3 or z=np.array(3)
z = np.asarray([z])
# y = z - Hx
# error (residual) between measurement and prediction
Hx = np.dot(H, x)
assert np.shape(Hx) == np.shape(z) or (np.shape(Hx) == (1,1) and np.shape(z) == (1,)), \
'shape of z should be {}, but it is {}'.format(
np.shape(Hx), np.shape(z))
self._y = z - Hx
# S = HPH' + R
# project system uncertainty into measurement space
S = dot3(H, P, H.T) + R
# K = PH'inv(S)
# map system uncertainty into kalman gain
K = dot3(P, H.T, linalg.inv(S))
# x = x + Ky
# predict new x with residual scaled by the kalman gain
self._x = x + np.dot(K, self._y)
# P = (I-KH)P(I-KH)' + KRK'
I_KH = self._I - np.dot(K, H)
self._P = dot3(I_KH, P, I_KH.T) + dot3(K, R, K.T)
self._S = S
self._K = K
self.log_likelihood = logpdf(z, np.dot(H, x), S)
def update_correlated(self, z, R=None, H=None):
if z is None:
return
if R is None:
R = self.R
elif isscalar(R):
R = eye(self.dim_z) * R
# rename for readability and a tiny extra bit of speed
if H is None:
H = self.H
x = self._x
P = self._P
M = self.M
# handle special case: if z is in form [[z]] but x is not a column
# vector dimensions will not match
if x.ndim==1 and shape(z) == (1,1):
z = z[0]
if shape(z) == (): # is it scalar, e.g. z=3 or z=np.array(3)
z = np.asarray([z])
# y = z - Hx
# error (residual) between measurement and prediction
self._y = z - dot(H, x)
# project system uncertainty into measurement space
S = dot3(H, P, H.T) + dot(H, M) + dot(M.T, H.T) + R
# K = PH'inv(S)
# map system uncertainty into kalman gain
K = dot(dot(P, H.T) + M, linalg.inv(S))
# x = x + Ky
# predict new x with residual scaled by the kalman gain
self._x = x + dot(K, self._y)
self._P = P - dot(K, dot(H, P) + M.T)
self._S = S
self._K = K
# compute log likelihood
self.log_likelihood = logpdf(z, dot(H, x), S)
def predict(self, u=0, B=None, F=None, Q=None):
if B is None:
B = self._B
if F is None:
F = self._F
if Q is None:
Q = self._Q
elif np.isscalar(Q):
Q = np.eye(self.dim_x) * Q
# x = Fx + Bu
self._x = np.dot(F, self.x) + np.dot(B, u)
# P = FPF' + Q
self._P = self._alpha_sq * dot3(F, self._P, F.T) + Q
def get_prediction(self, u=0):
x = dot(self._F, self._x) + dot(self._B, u)
P = self._alpha_sq * dot3(self._F, self._P, self._F.T) + self._Q
return (x, P)
def residual_of(self, z):
return z - dot(self.H, self._x)
def measurement_of_state(self, x):
return dot(self.H, x)
@property
def alpha(self):
return self._alpha_sq**.5
@property
def likelihood(self):
return math.exp(self.log_likelihood)
@alpha.setter
def alpha(self, value):
assert np.isscalar(value)
assert value > 0
self._alpha_sq = value**2
@property
def Q(self):
return self._Q
@Q.setter
def Q(self, value):
self._Q = setter_scalar(value, self.dim_x)
@property
def P(self):
return self._P
@P.setter
def P(self, value):
self._P = setter_scalar(value, self.dim_x)
@property
def F(self):
return self._F
@F.setter
def F(self, value):
self._F = setter(value, self.dim_x, self.dim_x)
@property
def B(self):
return self._B
@B.setter
def B(self, value):
if np.isscalar(value):
self._B = value
else:
self._B = setter (value, self.dim_x, self.dim_u)
@property
def x(self):
return self._x
@x.setter
def x(self, value):
self._x = setter_1d(value, self.dim_x)
@property
def K(self):
return self._K
@property
def y(self):
return self._y
@property
def S(self):
return self._Sfrom scipy.stats import norm, multivariate_normal
import pandas as pd, math
import numpy as np, numpy.linalg as linalg
import matplotlib.pyplot as plt
import kalman
def pos_vel_filter(x, P, R, Q=0., dt=1.0):
kf = kalman.KalmanFilter(dim_x=2, dim_z=1)
kf.x = np.array([x[0], x[1]]) # yer ve hiz
kf.F = np.array([[1., dt],
[0., 1.]]) # konum gecis matrisi
kf.H = np.array([[1., 0]]) # olcum fonksiyonu
kf.R *= R # olcum belirsizligi
if np.isscalar(P):
kf.P *= P # kovaryans matrisi
else:
kf.P[:] = P # [:] komutu derin kopya yapar
if np.isscalar(Q):
kf.Q = kalman.Q_discrete_white_noise(dim=2, dt=dt, var=Q)
else:
kf.Q[:] = Q
return kf
def compute_dog_data(z_var, process_var, count=1, dt=1.):
x, vel = 0., 1.
z_std = math.sqrt(z_var)
p_std = math.sqrt(process_var)
xs, zs = [], []
for _ in range(count):
v = vel + (np.random.randn() * p_std * dt)
x += v*dt
xs.append(x)
zs.append(x + np.random.randn() * z_std)
return np.array(xs), np.array(zs)
def run(x0=(0.,0.), P=500, R=0, Q=0, dt=1.0,
track=None, zs=None,
count=0, do_plot=True, **kwargs):
# Simulate dog if no data provided.
if zs is None:
track, zs = compute_dog_data(R, Q, count)
# create the Kalman filter
kf = pos_vel_filter(x0, R=R, P=P, Q=Q, dt=dt)
# run the kalman filter and store the results
xs, cov = [], []
for z in zs:
kf.predict()
kf.update(z)
xs.append(kf.x)
cov.append(kf.P)
xs, cov = np.array(xs), np.array(cov)
return xs, cov
P = np.diag([500., 49.])
Ms, Ps = run(count=50, R=10, Q=0.01, P=P)
print (Ms[-4:,])[[ 48.01227584 1.04168185]
[ 49.29870875 1.07239646]
[ 49.72124553 0.99084303]
[ 49.69899438 0.86370533]]plt.plot(range(len(Ms)), Ms[:,0])
plt.savefig('tser_kf_02.png')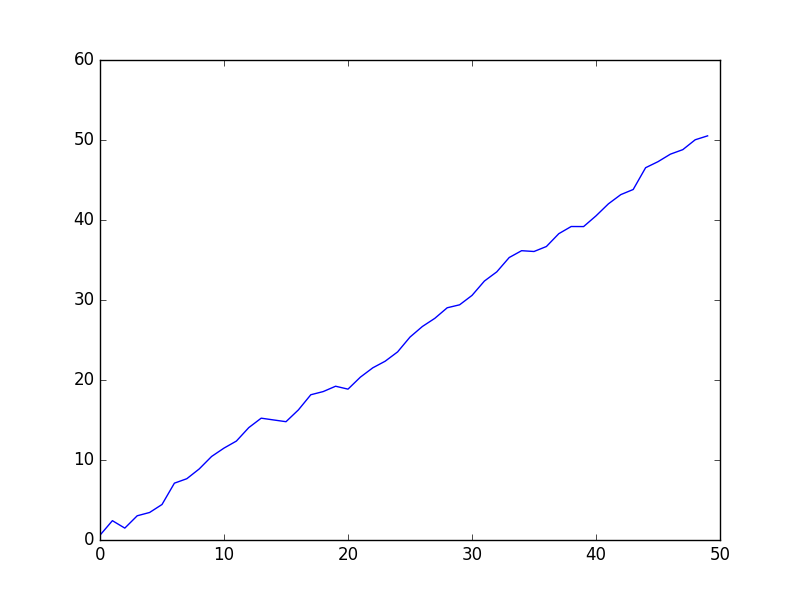
Kaynaklar
[1] Gelb, Applied Optimal Estimation
[2] Brown, osf. 143, Introduction to Random Signals and Applied Kalman Filtering
[3] Hartley, Zisserman, Multiple View Geometry
[4] Labbe, Kalman and Bayesian Filters in Python
[5] Bayramlı, Zaman Serileri, Ortalamaya Dönüş ile İşlem