Momentum Stratejileri
Momentum kelimesi akılda ivmeli bir hareketi çağrıştırıyor, yani olmakta olan bir gidişatın olmaya devam etmesi gibi görebiliriz bu kavramı. Bu tür bir kalıcılık, yukarı ya da aşağı doğru, borsacı için al/sat bağlamında önemli bir sinyaldir ve kar amaçlı olarak kullanılabilir.
Araştırmacılar bazen varlık fiyatlarındaki momentumu ikiye ayırıyorlar; zaman serisi momentumu ve kesitsel (cross-sectional) momentum. Zaman serisi momentumu basit: bir serinin gelecekteki getirisinin geçmişteki getirisi ile arasında pozitif korelasyon vardır. Kesitsel durumda ise izafi bir olay vardır: eğer bir serinin getirisi diğer serilerden daha iyi olmuş ise, bu performans büyük bir ihtimalle bu şekilde devam edecektir, ya da tersi durumda, kötü performans kötü olmaya devam edecektir.
Zaman serisi korelasyonunu ölçmek için istatistiki korelasyon hesabını kullanabiliriz, ki bu hesap ayrıca bir p-değeri de hesaplıyor (korelasyon olmadığı sıfır hipotezinin sıfır değeri), çok düşük p-değeri korelasyon varlığına dair bir işaret.
Korelasyon hesaplarken bir zaman adımı / gecikmesi (lag) seçmek lazım. Mesela 1 günlük bazında hesaplanmış geçmiş ve gelecek getirileri arasında negatif korelasyon bulunabilir, ama 20 günlük adımlar üzerinden hesaplanmış getirilerin 40 günlük adımlar üzerinden hesaplanmış gelecek getirileri arasında pozitif korelasyon bulunabilir. Bu tabii ki önemli çünkü bu bize 20 günlük sinyal üzerinden 40 günlük elde tutma (ya da açığa satma) işlemi yapmamız gerektiğini söylüyor.
Örnek olarak 2 yıllık Hazine Vadeli İşlem Sözleşmesinin (Treasury Future) fiyatını işleyelim. Bu varlığın geçmişteki ve gelecekteki farklı kombinasyondaki adımlar üzerindeki getirilerinin korelasyonunu test edeceğiz; mesela geçmiş getiriyi (lookback) 5 günlük adımlardan hesaplayıp, geleceği (hold days) 10 günlük adımlardan hesaplamak gibi. Ya da 10-10, 25-60, vs, ve tüm bu farklı kombinasyonların verilerinin ikili olarak korelasyonunu alıp onların p-değerini hesaplayacağız.
import sys; sys.path.append('../tser_draw_sharpe')
import pandas as pd
df = pd.read_csv('TU.csv')
import sys; sys.path.append('../tser_coint')
import corr
res = []
for lookback in [1, 5, 10, 25, 60, 120, 250]:
for holddays in [1, 5, 10, 25, 60, 120, 250]:
df_Close_lookback = df.Close.shift(lookback)
df_Close_holddays = df.Close.shift(-holddays)
df['ret_lag'] = (df.Close-df_Close_lookback)/df_Close_lookback
df['ret_fut'] = (df_Close_holddays-df.Close)/df.Close
dfc = df[['ret_lag','ret_fut']].dropna()
idx = None
if lookback >= holddays:
idx = np.array(range(0,len(dfc.ret_lag), holddays))
else:
idx = np.array(range(0,len(dfc.ret_lag), lookback))
dfc = dfc.ix[idx]
t, x, p = corr.p_corr(dfc.ret_lag, dfc.ret_fut)
res.append([lookback, holddays, t, p])
res = pd.DataFrame(res,columns=['geriye bakis','tutma gunu','korelasyon','p degeri'])
print res[res['geriye bakis'] >= 25]
geriye bakis tutma gunu korelasyon p degeri
21 25 1 -0.013846 0.270625
22 25 5 0.032196 0.263327
23 25 10 0.151663 0.017386
24 25 25 0.194388 0.045128
25 25 60 0.233075 0.021371
26 25 120 0.149209 0.102255
27 25 250 0.261104 0.015751
28 60 1 0.031111 0.088828
29 60 5 0.079022 0.063314
30 60 10 0.170948 0.009661
31 60 25 0.182575 0.059741
32 60 60 0.213958 0.123890
33 60 120 -0.036387 0.424304
34 60 250 0.318615 0.049219
35 120 1 0.021126 0.187942
36 120 5 0.053784 0.157502
37 120 10 0.092116 0.112675
38 120 25 0.152030 0.104487
39 120 60 -0.023771 0.451293
40 120 120 0.217406 0.227647
41 120 250 0.403921 0.085531
42 250 1 0.040612 0.058007
43 250 5 0.105563 0.034167
44 250 10 0.178648 0.014633
45 250 25 0.273233 0.018136
46 250 60 0.319392 0.064088
47 250 120 0.354586 0.142317
48 250 250 0.512954 0.188391
Kod bir anlamda her zaman anı için o andaki tarihsel getiri ve eğer o noktada pozisyon alınmış olsa eldeki varlığın tutulmasından elde edilecek getiri hesabını yapıyor. Bu iki hesaptan iki zaman serisi türetiliyor, sonra geriye bakış, tutma günü arasından ufak olanı oranında bu seri örnekleniyor (sample). Niye bu örnekleme? Bu lazım, çünkü geriye bakış, alış belli aralıklardan yapılır, çok ufak (ya da hiç) örnekleme yapsak birbiriyle çakışan hesapları üst üste görmüş olurduk.
Seçimimizi yapmak için en iyi korelasyon katsayısı ve p-değeri arasında bir denge gözetmek gerektiğini görüyoruz, bazen iyi olabilecek bir katsayı için p-değeri iyi olmayabiliyor. (60, 10), (60, 25), (250, 10), (250, 25), (250, 60), (250, 120) eşleri bu bağlamda en iyi dengede olanlar herhalde, ve al/sat yapmaya gelince bizim genel tercihimiz düşük elde tutma gününe ve ayrıca en yüksek Sharpe oranına sahip olan varlıklar tabii ki. Para kazanmak için 10 gün mü 100 gün mü beklemek daha iyi? Eğer getiriler kabaca iki tarafta eşit ise 10 gün tercihimiz!
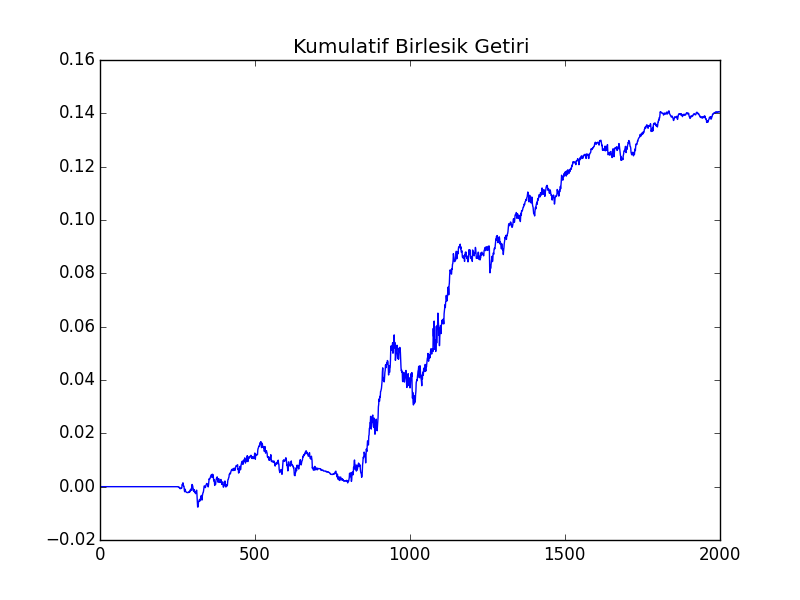
Şimdi getiriyi hesaplayalım. Bu hesap için 250,25 kombinasyonunu seçelim, bu kombinasyonun katsayısı 0.273233 p-değeri 0.018. Fena değil. Stratejiyi şöyle kodlayacağız, eğer geçmişteki 12 aylık (aşağı yukarı 250 gün) getiri pozitif ise, hisseyi alıp bu pozisyonda 1 ay (25 gün) dur. Pozitif / negatif bize al / sat yönünde sinyal çünkü korelasyon olduğunu biliyoruz ya artık, demek ki eskiden çıkmışsa gelecekte çıkacak, düşmüşse gelecekte düşecek. Bu bilinen bir strateji aslında ama biz onu biraz değiştirdik, al/sat kararını her ay vermeye çalışmak yerine her gün vereceğiz, ve her gün alım/satım için sermayemizin 1/25'ini kullanacağız.
import dd
def report(df,lookback,holddays):
longs = df.Close > df.Close.shift(lookback)
shorts = df.Close < df.Close.shift(lookback)
df['pos'] = 0.
for h in range(holddays):
long_lag = longs.shift(h).fillna(False)
short_lag = shorts.shift(h).fillna(False)
df.loc[long_lag,'pos'] += 1
df.loc[short_lag,'pos'] -= 1
ret=(df.pos.shift(1)* (df.Close-df.Close.shift(1)) / df.Close.shift(1)) \
/ holddays # sermayenin holddays'lik parcasini kullan
cumret=np.cumprod(1+ret)-1
print 'APR', ((np.prod(1.+ret))**(252./len(ret)))-1
print 'Sharpe', np.sqrt(252.)*np.mean(ret)/np.std(ret)
print 'Dusus Kaliciligi', dd.calculateMaxDD(np.array(cumret))
return cumret
cumret=report(dftu,lookback = 250,holddays = 25)
APR 0.0167080584229
Sharpe 1.04172346649
Dusus Kaliciligi (-0.024847461773700896, 343.0)
Tabii al/sat kararlaştırınca bu al ve satların 25 gün elde tutulması ve bunların birikmesi durumunu hesaplamak lazım, bunu da $h=0,1,..,25$ kadar kaydırıp bu kaydırılmış 25 vektörü toplayarak elde elde ediyoruz, mesela sadece 3 vektör için gösterelim,
+ + + ... - - + - ...
+ + + ... - - + - ...
+ + + ... - - + - ...
Üstteki ilk satır al/sat kararları, arka arkaya 3 al kararı var, bunlar toplana toplana 3. günde 3 birim varlık birikmiş olacak, aynı şekilde satlar eksiltilir, vs. Diğer hesaplar önceden gördüğümüz tanıdık getiri, kumulatif getiri hesapları.
plt.plot(cumret)
plt.title(u'Kümülatif Birleşik Getiri')
plt.savefig('tser_mom_01.png')
Aynı stratejiyi diğer bazı vadeli işlemler HG, BRE üzerinde kullanırsak,
dfhg = pd.read_csv('HG.csv')
cumret = report(dfhg,lookback = 40,holddays = 40)
APR 0.177399755457
Sharpe 1.04800326416
Dusus Kaliciligi (-0.23984679762413508, 424.0)
plt.plot(cumret)
plt.savefig('tser_mom_04.png')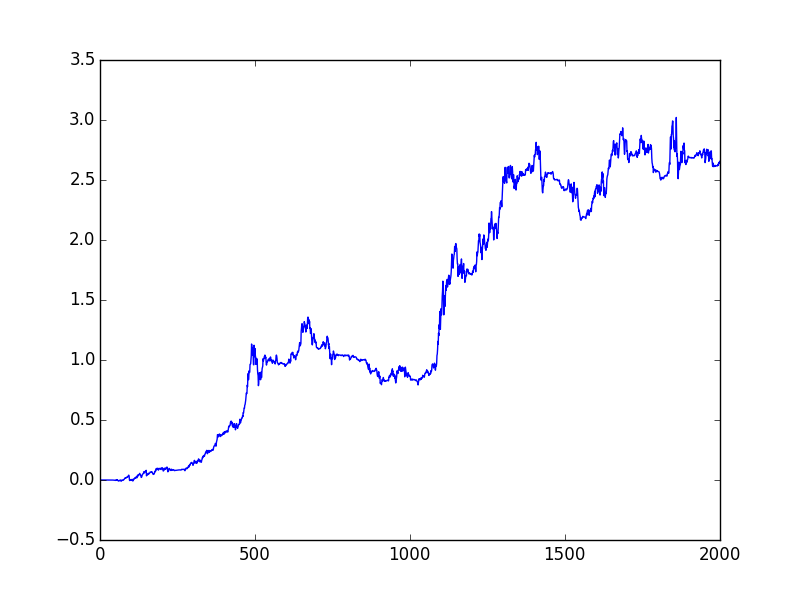
dfbre = pd.read_csv('BRE.csv')
cumret = report(dfbre,lookback = 100,holddays = 10)
APR 0.177086083041
Sharpe 1.08707778803
Dusus Kaliciligi (-0.14812255240727923, 191.0)
plt.plot(cumret)
plt.savefig('tser_mom_05.png')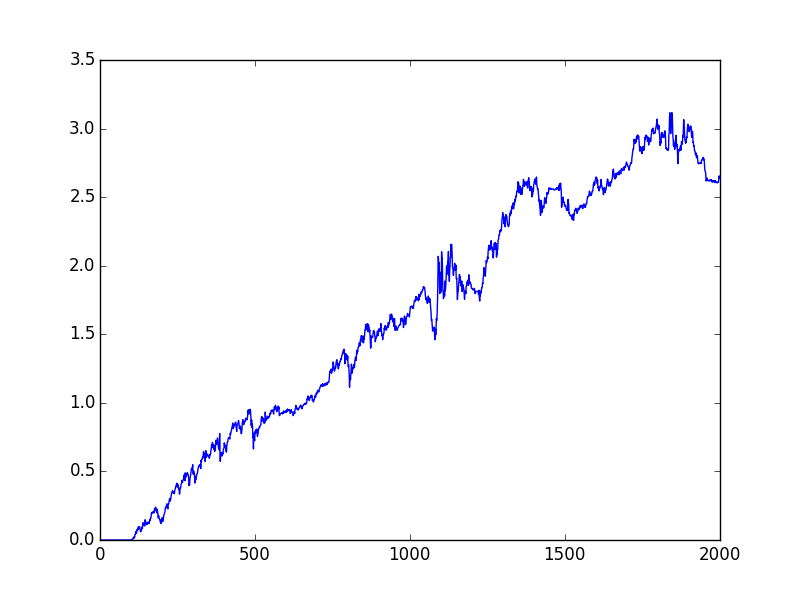
Boşluk Görünce Alım (Buy on Gap)
Değişik bir momentum stratejisi "boşluk görünce işlem yapmak". Mesela bir varlığın kapanış (close) getirilerini bir pencere üzerinden yürüyen ortalamayla (moving average) hesaplıyoruz, böylece bir baz şablon oluşturuyoruz, eğer bir günün açılış (open) fiyatı bu şablon getiri, çarpı önceki günün en yüksek (high) fiyatından belli oranda yüksek ise alım yapıyoruz, önceki günün en düşük (low) fiyatından belli oranda düşük ise satım yapıyoruz. Yani yükselme trendi var, bir momentum oluşmuş, bu devam ediyor, bu alım sinyalidir, ya da tersi olmuştur bu satış sinyalidir.
Altta FSTX sembolüne sahip Dow Jones STOXX 50 vadeli işlem sözleşmesinin (futures) üzerinde bu tekniği görebiliriz,
import pandas as pd, dd
df = pd.read_csv('FSTX.csv')
entryZscore=0.1
stdret = pd.rolling_mean(df.cl.pct_change(), window=90).shift(1)
longs = df.op >= df.hi.shift(1)*(1+entryZscore*stdret)
shorts = df.op <= df.lo.shift(1)*(1-entryZscore*stdret)
df['pos'] = 0
df.loc[longs,'pos'] = 1
df.loc[shorts,'pos'] = -1
ret=df.pos * (df.op-df.cl) / df.op
ret = ret.dropna()
cumret=np.cumprod(1+ret)-1
print 'APR', ((np.prod(1.+ret))**(252./len(ret)))-1
print 'Sharpe', np.sqrt(252.)*np.mean(ret)/np.std(ret)
print 'Dusus Kaliciligi', dd.calculateMaxDD(np.array(cumret))
APR 0.140771737387
Sharpe 1.35989260747
Dusus Kaliciligi (-0.14880173773680128, 190.0)
plt.plot(cumret)
plt.title(u'Kümülatif Birleşik Getiri')
plt.savefig('tser_mom_02.png')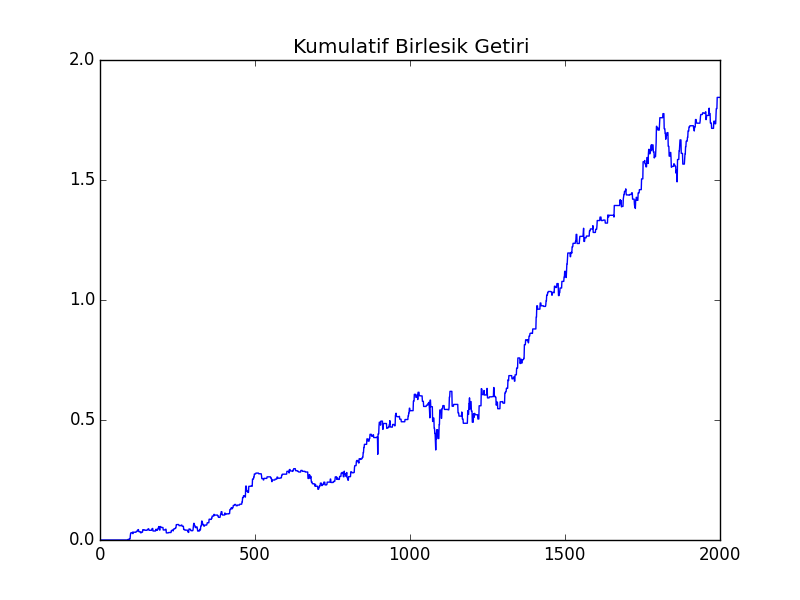
Şirket Kar Açıklamaları
Kar açıklamalarının şirket fiyatlarına momentum vermesi şaşırtıcı değil. Fakat bu açıklamanın ardından nispeten uzun bir süre bu etkinin sürmesi ilginç. Daha ilginç olan bu etki uzun süredir biliniyor ve kullanıla kullanıla etkisi yokolabilirdi, fakat bu hala gerçekleşmedi!
Kâr açıklamalarını kullanan strateji çok basit: açıklamanın "iyi" ya da "kötü" olduğunu bile bilmemize gerek yok, o sinyali almak için yine piyasanın kendisini kullanacağız. Eğer önceki gün kapanış sonrası bir açıklama yapılmışsa, ve yine önceki günün kapanışı ve bugünin açılışı üzerinden hesaplanan getiri "yeterince" pozitif ise (ki bunu hareketli standart sapmaya izafi olarak hesaplayacağız), senedi al, yoksa açığa sat, ve günün kapanışında tüm pozisyonlardan çık. Burada yapmaya uğraştığımız momentumu, bir senet etrafında olan "heyecanı" açılışın önceki günün kapanışına göre farkından anlamaya çalışmak.
Altta bu stratejinin S\&P 500 senetleri üzerinde ve Ocak 3, 2011, to Nisan 24, 2012 arasında geriye dönük testini görüyoruz. Şirket kar açıklamaları, açılış, kapanış fiyatları farklı matrisler içinde. Her matrisin kolonlarında şirketler var, satırları ise zaman. Geriye bakış zamanı 90 gün. Kar açıklama verisi earnings.com sitesinden alınmış.
import pandas as pd, zipfile, dd
with zipfile.ZipFile('earnann.zip', 'r') as z:
earnann = pd.read_csv(z.open('earnann.csv'),sep=',')
op = pd.read_csv(z.open('earnann-op.csv'),sep=',')
cl = pd.read_csv(z.open('earnann-cl.csv'),sep=',')
lookback=90
retC2O=(op-cl.shift(1)) / cl.shift(1)
stdC2O=pd.rolling_std(retC2O, window=lookback)
pos = pd.DataFrame(np.zeros(cl.shape),index=cl.index,columns=cl.columns)
longs=(retC2O >= 0.5*stdC2O).astype(int) * earnann
shorts=(retC2O <= -0.5*stdC2O).astype(int) * earnann;
pos = pos + longs - shorts
ret=(pos*(cl-op)/op).sum(axis=1)/30.
cumret=np.cumprod(1+ret)-1
print 'APR', ((np.prod(1.+ret))**(252./len(ret)))-1
print 'Sharpe', np.sqrt(252.)*np.mean(ret)/np.std(ret)
print 'Dusus Kaliciligi', dd.calculateMaxDD(np.array(cumret))
APR 0.0681264455203
Sharpe 1.49474260654
Dusus Kaliciligi (-0.026051533343801503, 109.0)
Üstteki hesapta 30'a böldük çünkü bir günde aşağı yukarı bu kadar kar açıklaması yapılıyor,
print earnann.sum(axis=1).max()
41
plt.plot(cumret)
plt.title(u'Kümülatif Birleşik Getiri')
plt.savefig('tser_mom_03.png')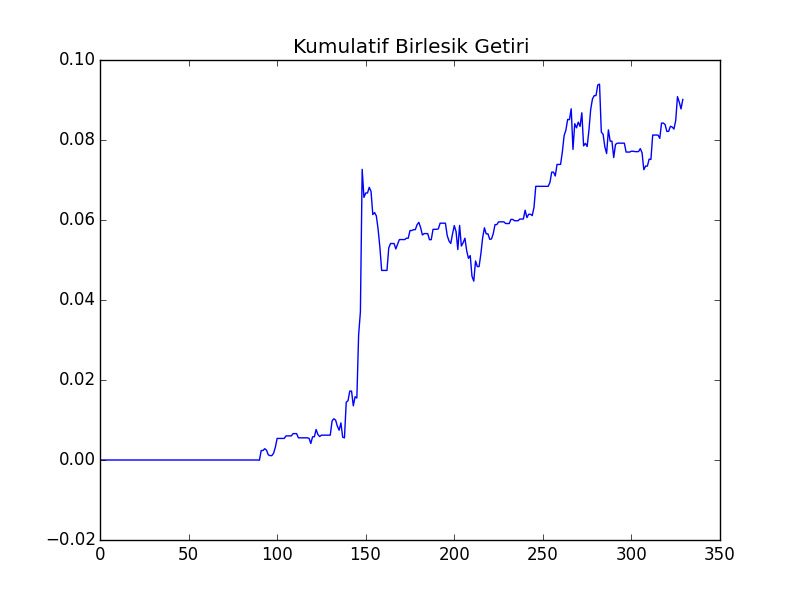
Üstel Yürüyen Ortalama (EWMA) ile Momentum
Pandas'in EWMA hesabı için bir çağrısı var, olağan durumunda üstelli katsayıları kullanır, fakat istenirse özyineli formda da hesap yapabilir. Pandas ile pencere gibi bir parametre var, buna kapsam (span) deniyor. Kapsam $k$ ile $\alpha$ arasındaki ilişki şöyle,
$$\alpha = 2/(k+1) $$
Örnek
Alım satım kararları için EWMA kullanılabilir. Bir fiyat serisinini iki tane ayrı EWMA'sı alınır. Bu ortalamalardan bir tanesi daha yavaş olarak addedilir, çünkü daha geniş bir kapsamda geriye bakar. Diğeri daha hızlı addedilir, daha kısa vadeli geriye bakar. Eğer daha hızlı olan ortalama daha yavaş olanın üzerindeyse fiyat serisi yukarı doğru bir trende girmiştir, alım yapılmalıdır, tersi var ise, satım trendine girilmiştir, satım yapılmalıdır.
Altta ham petrol vadeli işlem sözleşmesi (future) üzerinde örneği görüyoruz. İki kapsam var, 32 ve 128. EWMA'lar birbirinin üzerine çıktığı noktalar alım, satım anları olarak kullanılabilir.
import pandas as pd
df = pd.read_csv("oil_crude_future.csv")
df['hızlı'] = pd.ewma(df.price, span=32)
df['yavaş'] = pd.ewma(df.price, span=128)
df[['price','hızlı','yavaş']].plot()
plt.annotate('Sat',xy=(50,150),xytext=(100,160),\
arrowprops=dict(facecolor='black',width=1,shrink=0.05))
plt.annotate('Al',xy=(240,80),xytext=(200,100),\
arrowprops=dict(facecolor='black',width=1,shrink=0.05))
plt.savefig('tser_misc_01.png')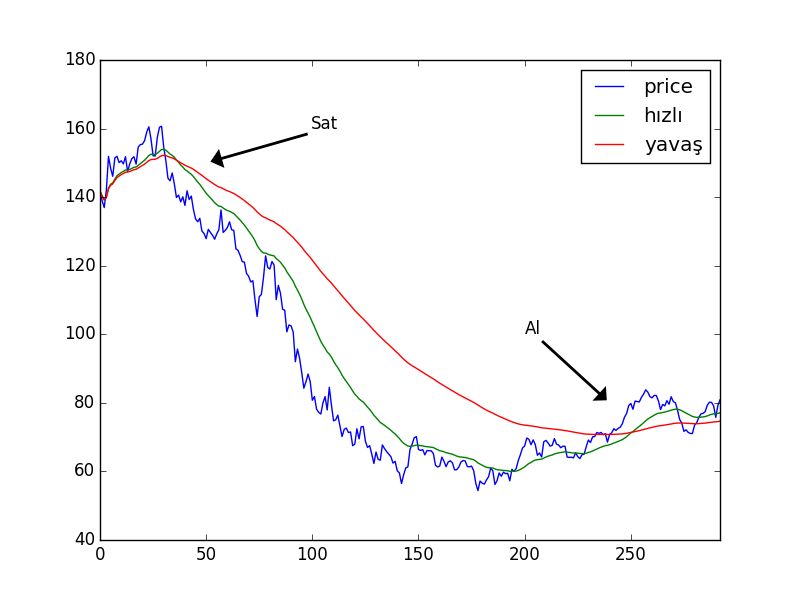
Tabii alım ve satım olma / olmama türünden ikisel kararlar değil. [2] alımda olma ve satıma olmayı sürekli bağlamda düşünüyor, yani üstteki örnekte hangi "pozisyonda" olunduğu hesabı için hızlı EWMAC'ten yavaş olan çıkartılıyor, ve bu fark kadar, ki bir reel sayı, posiyona giriliyor. Eğer sonuç -4.5 ise 4.5 ünite kadar açığa satışta olmak lazım.
Negatif Yamukluk (Negative Skew)
Momentum stratejilerinin, özelde EWMA stratejilerinin pozitif yamukluğu olduğu hep söylenir. Böyle olup olmadığını kontrol edelim.
import sys; sys.path.append('../tser_voltar')
import util, pandas as pd, zipfile
f = 'CORN_price.csv'
with zipfile.ZipFile('../tser_voltar/legacycsv.zip', 'r') as z:
df = pd.read_csv(z.open(f),sep=',',index_col=0,parse_dates=True)
pred = util.ewma(df.PRICE,2,8)
print util.skew(df.PRICE, pred)
1.18
Daha "yavaş" EWMA stratejilerinde negatif yamukluk görülebilir, hızlı olanda görülmüyor çünkü bu strateji daha hızlı adapte oluyor, [2]'nin tarif ettiği gibi uzun zaman azar azar kaybedip düşüş veya çıkış başlayınca birdenbire kazanç sağlıyor.
Kaynaklar
[1] Chan, Algorithmic Trading
[2] Carver, Systematics Trading
Yukarı