Sezonsallık, Periyotlar
Zaman serilerini trendini, sezonsallığını nasıl inceleriz, ve trendde değişim varsa bunu nasıl yakalarız?
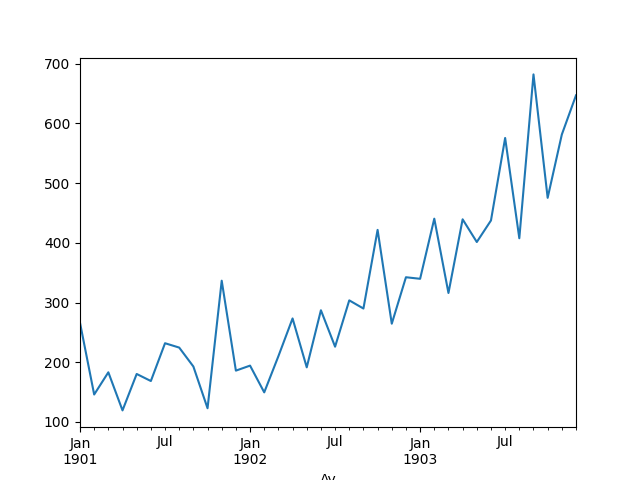
Bir örnek üzerinde görelim, bir şirketin şampuan satış kazancı, veri [1]'den,
import pandas as pd
def parser(x):
return pd.datetime.strptime( '190'+x, '%Y-%m' )
df = pd.read_csv('shampoo-sales.csv', header=0, index_col=0, \
parse_dates=True, date_parser=parser)
df.Satis.plot()
plt.savefig('tser_022_de_07.png')
Yukarı doğru bir trend var. Bu trendi veriye bir düz çizgi uydurarak (fit), yani
tek değişkenli, ikinci derece lineer regresyon yaparak yakalayabiliriz. Bunu
yapmayı pek çok diğer derste gösterdik, statsmodels.regression
paketinden, linear_model.OLS ile, statsmodels.formula.api ile,
ya da direk Lineer Cebir kullanarak.. Altta polyfit çağrısı
kullanılacak.
Modelden gelen katsayıları (coefficients) kullanıp tahmini $y$ değerleri üretmek için alttaki fonksiyon var,
def model_compute(X, coef):
degree = len(coef)-1
curve = [np.sum([coef[-1]] + [x**(degree-d)*c for d,c \
in enumerate(coef[:-1])]) for x in X]
return curve
Uydurmayı yapıp modeli veri üzerinde gösterelim,
X = np.array(range(len(df))).reshape(-1)
y = df.values.reshape(-1)
degree = 1
coef = np.polyfit(X, y, degree)
df['Model'] = model_compute(X, coef)
df.plot()
plt.savefig('tser_022_de_01.png')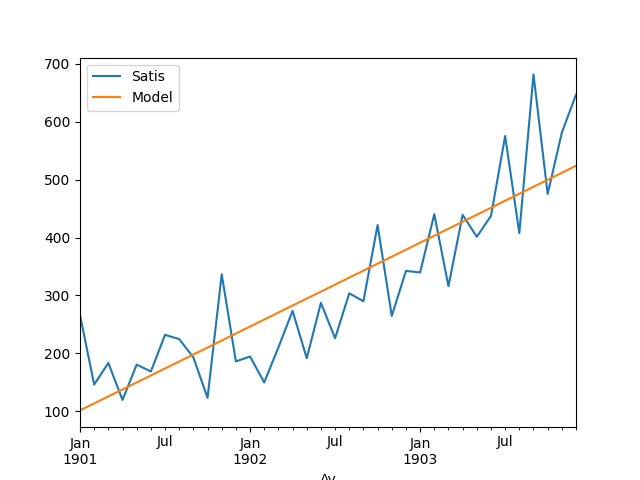
Veriden "trendi çıkartabiliriz". Bunu basit bir şekilde veriden modeli eksilterek yapabiliriz. Bu durumda geriye kalan sadece trend haricinde olan şeyler olacaktır. Trend çıkartmanın pek çok amacı olabilir, belki trend haricinde olan kalıpları, eğer hala varsa, görmek istiyoruz, ya da modelin artığına (residual) bakarak onun gürültü olup olmadığını anlamak istiyoruz. Bilindiği gibi lineer regresyonun faraziyesi verinin model artı gürültü olduğudur, o zaman model veriden çıkartılınca geriye kalan artık, "tortu" sadece gürültüdür. Gürültünün matematiksel tanımı Gaussian, ya da Normal dağılımıdır, demek ki artıklar üzerinde normallik testi bir anlamda modelin uyma başarısını da ölçer.
detrended = df.Satis-df.Model
detrended.plot()
plt.savefig('tser_022_de_03.png')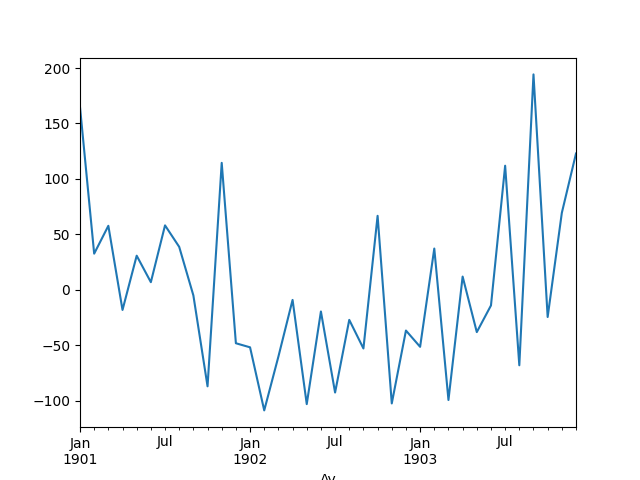
Normallik testini uygulayalım,
from scipy import stats
val,pval = stats.shapiro(detrended)
print ('p degeri =', pval)
p degeri = 0.09782794862985611
Shapiro-Wilk testinde p-değerinin 0.05'ten küçük olması normalliğin reddedilmesi demektir. Üstte normal olmadığın reddedemedik, demek ki büyük ihtimalle elimizde bir Normal dağılım var.
Sezonsallık
Benzer bir şekilde sezonsallığı da modelleyebiliriz. Sezonsallık bir periyotsallığı ima eder, o zaman en genel şekilde bir sinüs fonksiyonunu veriye uydurabiliriz. Fakat bu sinüs fonksiyonunun benliğini, başlangıç noktasını bilmiyoruz, bu durumlarda [6]'da sinüssel regresyon tekniğini gördük. Fakat belki de daha rahatı veriye bir 4'üncü derece polinom uydurmaktır.
Bu garip gelebilir, polinom uydurmayı çoğunlukla ikinci, üçüncü derecede eğrileri modelleyen çerçevede görmüş olabiliriz, bu yaklaşım fakat periyotsal fonksiyonları da çok rahat temsil edebiliyor. Sebebi herhalde sinüs fonsiyonunun Taylor açılımında [3] gizli, Taylor açılımında sonsuza kadar giden türevler polinom açılımda kullanılır, sinüsün 1'den 4'e kadar olan türevlerine bakarsak,
$\sin^{\prime}(x)=\cos(x),\quad$ $\sin^{\prime\prime}(x)=-\sin(x),\quad$, $\sin^{\prime\prime\prime}(x)=-\cos(x),\quad$, $\sin^{(4)}(x)=\sin(x)$.
Dördüncü türevin tekrar $\sin(x)$'a dönüş yaptığını görüyoruz. Demek ki 4'üncü derece polinom açılımı periyotsal fonksiyonları temsil etmek için yeterlidir.
Altta bir bölgeden alınmış günlük, o günün minimum hava sıcaklığı ölçümlerini görüyoruz. Ona modeli uyduralım,
import pandas as pd
df = pd.read_csv('daily-min-temperatures.csv', header=0,\
index_col=0, parse_dates=True)
X = [i%365 for i in range(0, len(df))]
y = df.values
degree = 4
coef = np.polyfit(X, y, degree)
df['Model'] = model_compute(X, coef)
df.plot()
plt.savefig('tser_022_de_02.png')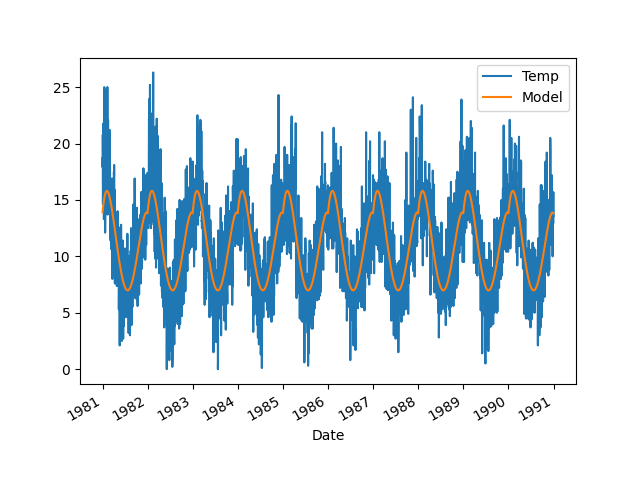
Periyotsallık yakalanmış gibi duruyor. Sezonsallığı veriden çıkartalım,
deseasoned = df.Temp-df.Model
deseasoned.plot()
plt.savefig('tser_022_de_04.png')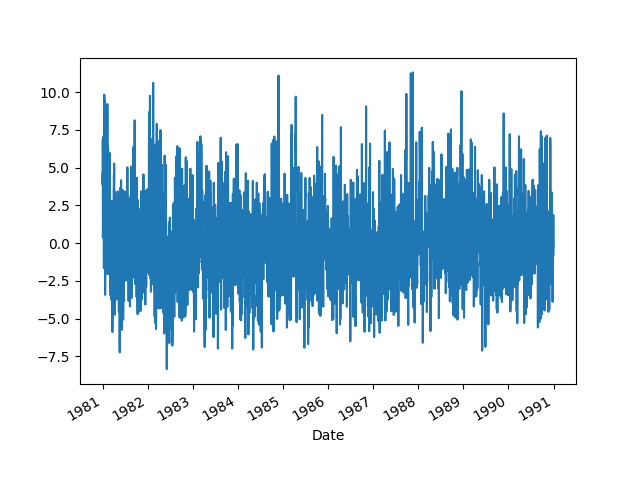
Artıklar üzerinde normallik testi,
from scipy import stats
val,pval = stats.shapiro(deseasoned)
print ('p degeri =', pval)
p degeri = 4.155807920014354e-10
Normal değil. Bunun sebebi veri içinde birden fazla sezonsallık, ya da başka bir örüntünün hala mevcut olması olabilir. Bu senaryoları test etmek ödev olsun.
Sinüssel Regresyon (Sinusoidal Regression)
Alttaki veriye bir veya birden fazla sinüs eğrisi uydurmak istiyoruz.
import pandas as pd
df = pd.read_csv('baltic.csv')
df.plot(x='toy',y='degs',kind='scatter')
plt.savefig('tser_sinreg_01.png')
Fakat sinüs eğrisini, tek sinüs eğrisi olduğu durumda bile, nasıl yana kaydırarak tam doğru noktayı bulacağız? Ayrıca eğrinin genliği (amplitude) önemli. Tüm bunları kapsayan formül
$$ f(x) = A \sin (x+\varphi) $$
Genlik $A$ ile faz ise $\varphi$ ile gösterilmiş, öyle bir $A,\varphi$ bulalım ki sonuç sinüs eğrisi tam veriye uysun. Veriye uydurma deyince akla lineer regresyon geliyor, fakat üstteki formülü olduğu gibi regresyona sokmak mümkün değil, çünkü faz kaydırmak için $\sin$ içindeki parametrenin değişmesi lazım, regresyon bunları yapamaz. Ama regresyona problemi `katsayı çarpı basit formül" şeklinde sunabilir miyiz acaba? Bir trigonometrik eşitlikten biliyoruz ki
$$ A \sin (x+\varphi) = a\sin(x) + b\cos(x) $$
ki $\sin\varphi = \frac{b}{\sqrt{a^2+b^2}}$, ve $A = \sqrt{a^2+b^2}$ olacak sekilde.
Bu eşitliğin doğru olduğunu kontrol edelim,
$$ a \sin(x) + b \cos(x) = \sqrt{a^2+b^2} \left(\frac{a}{\sqrt{a^2+b^2}} \sin(x) + \frac{b}{\sqrt{a^2+b^2}} \cos(x)\right) $$
$$ = A\left[\sin(x)\cos(\varphi) + \cos(x)\sin(\varphi)\right] $$
$$ = A\sin(x+\varphi) $$
O zaman $a \sin(x) + b \cos(x)$ için regresyon yapabiliriz. Regresyon iki toplam üzerinden tanımlı fonksiyonlar için en uygun $a,b$ katsayılarını hesaplayacak. Önce $\sin$ içinde $2\pi x$ ile başlarız,
import statsmodels.formula.api as smf
results = smf.ols('degs ~ np.sin(2*np.pi*toy) + np.cos(2*np.pi*toy)', data=df).fit()
print results.summary()
OLS Regression Results
==============================================================================
Dep. Variable: degs R-squared: 0.969
Model: OLS Adj. R-squared: 0.968
Method: Least Squares F-statistic: 704.3
Date: Fri, 12 May 2017 Prob (F-statistic): 1.10e-34
Time: 16:01:50 Log-Likelihood: -63.360
No. Observations: 48 AIC: 132.7
Df Residuals: 45 BIC: 138.3
Df Model: 2
Covariance Type: nonrobust
===========================================================================================
coef std err t P>|t| [95.0% Conf. Int.]
-------------------------------------------------------------------------------------------
Intercept 8.2917 0.135 61.407 0.000 8.020 8.564
np.sin(2 * np.pi * toy) -5.9156 0.191 -30.979 0.000 -6.300 -5.531
np.cos(2 * np.pi * toy) -4.0463 0.191 -21.190 0.000 -4.431 -3.662
==============================================================================
Omnibus: 28.673 Durbin-Watson: 1.051
Prob(Omnibus): 0.000 Jarque-Bera (JB): 4.298
Skew: -0.158 Prob(JB): 0.117
Kurtosis: 1.569 Cond. No. 1.41
==============================================================================
Warnings:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
a,b = results.params[1],results.params[2]
A = (a**2+b**2)
print A, np.rad2deg(np.arcsin(b**2 / A))
51.3672864144 18.5866613969
fit1 = results.params[0] + results.params[1] * np.sin(2*np.pi*df.toy) + \
results.params[2] * np.cos(2*np.pi*df.toy)
plt.scatter(df.toy,df.degs)
plt.hold(True)
plt.plot(df.toy,fit1)
plt.savefig('tser_sinreg_02.png')
Uyum fena değil. Daha iyi uyum için daha fazla terim ekleyebiliriz, mesela $\sin,\cos$ içinde $2 \pi x$ kullandık, bir de $4 \pi x$'li terimler ekleyerek,
import statsmodels.formula.api as smf
formula = 'degs ~ np.sin(2*np.pi*toy) + np.cos(2*np.pi*toy) + ' + \
' np.sin(4*np.pi*toy) + np.cos(4*np.pi*toy)'
results = smf.ols(formula, data=df).fit()
print results.summary()
OLS Regression Results
==============================================================================
Dep. Variable: degs R-squared: 0.999
Model: OLS Adj. R-squared: 0.999
Method: Least Squares F-statistic: 9519.
Date: Fri, 23 Sep 2016 Prob (F-statistic): 9.48e-63
Time: 10:56:56 Log-Likelihood: 16.130
No. Observations: 48 AIC: -22.26
Df Residuals: 43 BIC: -12.90
Df Model: 4
Covariance Type: nonrobust
===========================================================================================
coef std err t P>|t| [95.0% Conf. Int.]
-------------------------------------------------------------------------------------------
Intercept 8.2917 0.026 314.450 0.000 8.238 8.345
np.sin(2 * np.pi * toy) -5.9156 0.037 -158.634 0.000 -5.991 -5.840
np.cos(2 * np.pi * toy) -4.0463 0.037 -108.506 0.000 -4.122 -3.971
np.sin(4 * np.pi * toy) 1.2124 0.037 32.513 0.000 1.137 1.288
np.cos(4 * np.pi * toy) 0.3333 0.037 8.939 0.000 0.258 0.409
==============================================================================
Omnibus: 0.473 Durbin-Watson: 2.983
Prob(Omnibus): 0.790 Jarque-Bera (JB): 0.338
Skew: -0.200 Prob(JB): 0.845
Kurtosis: 2.909 Cond. No. 1.41
==============================================================================
Warnings:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
fit2 = results.params[0] + \
results.params[1] * np.sin(2*np.pi*df.toy) + \
results.params[2]*np.cos(2*np.pi*df.toy) + \
results.params[3] * np.sin(4*np.pi*df.toy) + \
results.params[4]*np.cos(4*np.pi*df.toy)
plt.scatter(df.toy,df.degs)
plt.hold(True)
plt.plot(df.toy, fit2)
plt.savefig('tser_sinreg_03.png')
Uyum daha iyi hale geldi.
Bir tane de mutlak değer içeren bir fonksiyon.
import pandas as pd
x = np.linspace(0,10,400)
y = np.abs(np.sin(2*np.pi*x)) + np.random.random(len(x)) * 0.5
df = pd.DataFrame(x)
df['y'] = y
df.columns = ['x','y']
df.plot(x='x',y='y')
plt.savefig('tser_sinreg_04.png')
import statsmodels.formula.api as smf
results = smf.ols('y ~ np.abs(np.sin(2*np.pi*x)) + np.abs(np.cos(2*np.pi*x))', data=df).fit()
print results.summary()
OLS Regression Results
==============================================================================
Dep. Variable: y R-squared: 0.830
Model: OLS Adj. R-squared: 0.829
Method: Least Squares F-statistic: 967.6
Date: Fri, 23 Sep 2016 Prob (F-statistic): 2.30e-153
Time: 17:23:34 Log-Likelihood: 209.20
No. Observations: 400 AIC: -412.4
Df Residuals: 397 BIC: -400.4
Df Model: 2
Covariance Type: nonrobust
=================================================================================================
coef std err t P>|t| [95.0% Conf. Int.]
-------------------------------------------------------------------------------------------------
Intercept 0.0995 0.074 1.351 0.177 -0.045 0.244
np.abs(np.sin(2 * np.pi * x)) 1.1266 0.059 19.195 0.000 1.011 1.242
np.abs(np.cos(2 * np.pi * x)) 0.1125 0.059 1.910 0.057 -0.003 0.228
==============================================================================
Omnibus: 171.148 Durbin-Watson: 2.049
Prob(Omnibus): 0.000 Jarque-Bera (JB): 22.018
Skew: 0.024 Prob(JB): 1.66e-05
Kurtosis: 1.852 Cond. No. 20.5
==============================================================================
Warnings:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
Kaynaklar
[1] Cross Validated, How to find a good fit for semisinusoidal model in R?, http://stats.stackexchange.com/questions/60500/how-to-find-a-good-fit-for-semi-sinusoidal-model-in-r
Yukarı