Özellik İşlemek (Feature Engineering)
Veri madenciliğinde "veriden veri yaratma" tekniği çok kullanılıyor; mesela bir sipariş veri satırında o siparişin hangi zamanda (timestamp) olduğunu belirten bir kolon varsa (ki çoğu zaman vardır), bu kolonu "parçalayarak" ek, daha genel, özetsel bilgi kolonları yaratılabilir. Ya da kategoriksel verileri pek çok farklı şekilde sayısal hale çevirebiliriz, mesela 1-hot kodlama ile N kategori N kolon haline gelir, eldeki kategoriye tekabül eden öğe 1 diğerleri sıfır yapılır.
Özellik işlemenin önemi yapay öğrenme açısından önemi var, mesela bir SVM sınıflayıcısını en basit haliyle siyah/beyaz görüntüden sayı tanıma probleminde kullandık, ve diyelim yüzde 70 başarı elde ettik. Şimdi çok basit bir yeni özellik yaratalım, görüntüyü dikey ikiye bölelim, ve üstteki ve alttaki siyah noktaları toplayarak iki yeni kolon olarak görüntü matrisine ekleyelim. Bu yeni özellikleri kullanınca basit sınıflayıcının yüzde 20 kadar tanıma başarısında ilerleme kaydettiğini göreceğiz!
Not: Derin yapay sınır ağları teknikleri ile özellik işlemeye artık gerek olmadığı söylenir, bu büyük ölçüde doğru. Bir DYSA farklı seviyelerdeki pek çok farklı nöronları üzerinden aslında üstte tarif edilen türden yeni özellikleri otomatik olarak yaratır, ögrenir. Fakat yine de yeni özellikleri elle yaratma tekniklerini bilmek iyi.
Şimdi farklı yöntemlere bakalım.
Zaman Kolonlarını Zenginleştirmek
Zaman kolonları çoğu zaman saniyeye kadar kaydedilir, bu bilgiyi alıp mesela ay, mevsim, haftanın günü, saat, iş saati mi (9-5 arası), akşam mı, sabah mı, öğlen mi, vs. gibi ek bilgiler çıkartılabilir. Tüm kolonlar veri madenciliği algoritmasına verilir, ve algoritma belki öğlen saati ile sipariş verilmiş olması arasında genel bir bağlantı bulacaktır.
Python + Pandas ile bir zaman kolonu şöyle parçalanabilir, örnek veri üzerinde görelim, sadece iki kolon var, müşteri no, ve sipariş zamanı,
import pandas as pd
from StringIO import StringIO
s = """customer_id;order_date
299;2012-07-20 19:44:55.661000+01:00
421;2012-02-17 21:54:15.013000+01:00
437;2012-02-20 22:18:12.021000+01:00
463;2012-02-20 23:46:21.587000+01:00
482;2012-05-21 09:50:02.739000+01:00
607;2012-02-21 11:57:12.462000+01:00
641;2012-02-21 13:40:28.088000+01:00
674;2012-08-21 14:53:15.851000+01:00
780;2012-02-23 10:31:05.571000+01:00
"""
df = pd.read_csv(StringIO(s),sep=';', parse_dates=True)
def f(x):
tmp = pd.to_datetime(x['order_date'])
tpl = tmp.timetuple(); yymm = int(tmp.strftime('%m%d'))
spring = int(yymm >= 321 and yymm < 621)
summer = int(yymm >= 621 and yymm < 921)
fall = int(yymm >= 921 and yymm < 1221)
winter = int( spring==0 and summer==0 and fall==0 )
warm_season = float(tpl.tm_mon >= 4 and tpl.tm_mon <= 9)
work_hours = float(tpl.tm_hour > 9 and tpl.tm_hour < 17)
morning = float(tpl.tm_hour >= 7 and tpl.tm_hour <= 11)
noon = float(tpl.tm_hour >= 12 and tpl.tm_hour <= 14)
afternoon = float(tpl.tm_hour >= 15 and tpl.tm_hour <= 19)
night = int (morning==0 and noon==0 and afternoon==0)
return pd.Series([tpl.tm_hour, tpl.tm_mon,
tpl.tm_wday, warm_season,
work_hours, morning, noon, afternoon, night,
spring, summer, fall, winter])
cols = ['ts_hour','ts_mon','ts_wday','ts_warm_season',\
'ts_work_hours','ts_morning','ts_noon','ts_afternoon',\
'ts_night', 'ts_spring', 'ts_summer', 'ts_fall', 'ts_winter']
df[cols] = df.apply(f, axis=1)
print df[cols]
ts_hour ts_mon ts_wday ts_warm_season ts_work_hours ts_morning \
0 18.0 7.0 4.0 1.0 0.0 0.0
1 20.0 2.0 4.0 0.0 0.0 0.0
2 21.0 2.0 0.0 0.0 0.0 0.0
3 22.0 2.0 0.0 0.0 0.0 0.0
4 8.0 5.0 0.0 1.0 0.0 1.0
5 10.0 2.0 1.0 0.0 1.0 1.0
6 12.0 2.0 1.0 0.0 1.0 0.0
7 13.0 8.0 1.0 1.0 1.0 0.0
8 9.0 2.0 3.0 0.0 0.0 1.0
ts_noon ts_afternoon ts_night ts_spring ts_summer ts_fall ts_winter
0 0.0 1.0 0.0 0.0 1.0 0.0 0.0
1 0.0 0.0 1.0 0.0 0.0 0.0 1.0
2 0.0 0.0 1.0 0.0 0.0 0.0 1.0
3 0.0 0.0 1.0 0.0 0.0 0.0 1.0
4 0.0 0.0 0.0 1.0 0.0 0.0 0.0
5 0.0 0.0 0.0 0.0 0.0 0.0 1.0
6 1.0 0.0 0.0 0.0 0.0 0.0 1.0
7 1.0 0.0 0.0 0.0 1.0 0.0 0.0
8 0.0 0.0 0.0 0.0 0.0 0.0 1.0
Sıcak mevsim (warm season) Mart-Eylül aylarını kapsar, bu ikisel bir değişken hale getirildi. Belki siparişin, ya da diğer başka bir verinin bununla bir alakası vardır. Genel 4 sezon tek başına yeterli değil midir? Olabilir, fakat bazı kalıplar / örüntüler (patterns) belki sıcak / soğuk mevsim bilgisiyle daha çok bağlantılıdır.
Aynı şekilde saat 1-24 arasında bir sayı olarak var, fakat "iş saatini" ayrı bir ikisel değişken olarak kodlamak yine bir "kalıp yakalama" şansımızı arttırabilir. Bu kolonun ayrı bir şekilde kodlanmış olması veri tasarımı açısından ona önem verildiğini gösterir, ve madencilik algoritmaları bu kolonu, eğer ona bağlı bir kalıp var ise, yakalayabilirler.
Not: Burada ufak bir pürüz sabah, öğlen, akşamüstü gibi zamanları kodlarken çıktı. Gece 19'dan sonra ve 7'den önce bir sayı olacaktı, fakat bu durumda $x>19$ ve $x<7$ hiçbir sonuç getirmeyecekti. Burada saatlerin 24 sonrası başa dönmesi durumu problem çıkartıyordu, tabii ki karşılaştırma ifadelerini çetrefilleştirerek bu iş çözülebilir, ama o zaman kod temiz olmaz (mesela ($x>19$ ve $x<24$) ya da ($x>0$ ve $x<7$) yapabilirdik). Temiz kod için gece haricinde diğer tüm seçenekleri kontrol ediyoruz, ve gece "sabah, öğlen, akşamüstü olmayan şey" haline geliyor. Aynı durum mevsimler için de geçerli. Onun için
night = int (morning==0 and noon==0 and afternoon==0)
kullanıldı.
Kategorileri İkileştirme
Yapay öğrenim algoritmalarının çoğu zaman hem kategorik hem sayısal değerleri aynı anda bulunduran verilerle iş yapması gerekebiliyor. Ayrıca literatüre bakılınca görülür ki çoğunlukla bir algoritma ya biri, ya diğeri ile çalışır, ikisi ile aynı anda çalışmaz (çalışanlar var tabii, mesela karar ağaçları -decision tree-). Bu gibi durumlarda iki seçenek var, ya numerik veri kategoriselleştirilir (ayrıksallaştırılır), ya da kategorik veri numerik hale getirilir.
Bu durumda, kategorik bir kolon eyalet için, eyaletin Ohio olup olmaması başlı başına ayrı bir kolon olarak gösteriliyor. Aynı şekilde Nevada. Bu kodlamaya literatürde 1-hot kodlaması adı veriliyor. KMeans, lojistik regresyon gibi metotlara girdi vermek için bu transformasyon kullanılabilir.
import numpy as np
import pandas as pd, os
import scipy.sparse as sps
from sklearn.feature_extraction import DictVectorizer
def one_hot_dataframe(data, cols, replace=False):
vec = DictVectorizer()
mkdict = lambda row: dict((col, row[col]) for col in cols)
vecData = pd.DataFrame(vec.fit_transform(data[cols].apply(mkdict, axis=1)).toarray())
vecData.columns = vec.get_feature_names()
vecData.index = data.index
if replace is True:
data = data.drop(cols, axis=1)
data = data.join(vecData)
return (data, vecData, vec)
data = {'state': ['Ohio', 'Ohio', 'Ohio', 'Nevada', 'Nevada'],
'year': [2000, 2001, 2002, 2001, 2002],
'pop': [1.5, 1.7, 3.6, 2.4, 2.9]}
df = pd.DataFrame(data)
df2, _, _ = one_hot_dataframe(df, ['state'], replace=True)
print df2
pop year state=Nevada state=Ohio
0 1.5 2000 0.0 1.0
1 1.7 2001 0.0 1.0
2 3.6 2002 0.0 1.0
3 2.4 2001 1.0 0.0
4 2.9 2002 1.0 0.0
Unutmayalım, kategorik değerler bazen binleri bulabilir (hatta sayfa
tıklama tahmini durumunda mesela milyonlar, hatta milyarlar), bu da
binlerce yeni kolon demektir. Yani 1/0 kodlaması, yani 1-hot işleminden ele
geçen yeni blok içinde aslında oldukca çok sayıda sıfır değeri olacak
(sonuçta her satırda binlerce 'şey' içinde sadece bir tanesi 1 oluyor),
yani bu bloğun bir seyrek matris olması iyi olurdu. O zaman matrisin
tamamını sps.csr_matrix ya da sps.lil_matrix ile gerçekten
seyrek formata çevirebiliriz, ve mesela scikit-learn paketi, numpy, scipy
işlemleri seyrek matrisler ile hesap yapabilme yeteneğine
sahip. Seyrekselleştirince ne elde ediyoruz? Sıfırları depolamadığımız
için sadece sıfır olmayan değerler ile işlem yapıyoruz, o ölçüde kod
hızlanıyor, daha az yer tutuyor.
Dikkat etmek gerekir ki yeni kolonları üretince değerlerin yerleri sabitlenmiş olur. Her satır bazında bazen state=Ohio, state=Nevada, bazen sadece state=Ohio üretiyor olamayız. Üstteki örnekte her zaman 4 tane kolon elde edilmelidir.
Not: 1-hot yerine bir diğer seçenek kategoriyi bir indise çevirmek (tüm kategorileri sıralayıp kaçıncı olduğuna bakarak mesela) sonra bu sayıyı ikisel sistemde belirtmek, eğer 'a' sayısı 30 indisine tekabül ediyorsa, 30 ikisel sistemde 11110, bu değer kullanılır (aslında bu son tarif edilen sistemin 1-hot sistemden daha iyi işlediği rapor ediliyor).
Anahtarlama Numarası (1-Hot Encoding, Hashing Trick)
Fakat bir problem var, dokümanı temsil eden ve içinde 1 ya da 0 hücreli özellik vektörünü (feature vector) oluşturmak için tüm kelimelerin ne olduğunu bilmeliyiz. Yani veriyi bir kere baştan sonra tarayarak bir sözlük oluşturmalıyız (ki öyle yapmaya mecbur kaldık) ve ancak ondan sonra her doküman için hangi kelimenin olup olmadığını saptamaya ve onu kodlamaya başlayabiliriz. Halbuki belgelere bakar bakmaz, teker teker giderken bile hemen bir özellik vektörü oluşturabilseydik daha iyi olmaz mıydı?
Bunu başarmak için anahtarlama numarasını kullanmamız lazım. Bilindiği gibi temel yazılım bilime göre bir kelimeyi temsil eden bir anahtar (hash) üretebiliriz, ki bu hash değeri bir sayıdır. Bu sayının en fazla kaç olabileceğinden hareketle (hatta bu sayıya bir limit koyarak) özellik vektörümüzün boyutunu önceden saptamış oluruz. Sonra kelimeye bakarız, hash üretiriz, sonuç mesela 230 geldi, o zaman özellik vektöründeki 230'uncu kolonun değerini 1 yaparız.
d_input = dict()
def add_word(word):
hashed_token = hash(word) % 127
d_input[hashed_token] = d_input.setdefault(hashed_token, 0) + 1
add_word("obama")
print d_input
{48: 1}
add_word("politics")
print d_input
{48: 1, 91: 1}
Üstteki kodda bunun örneğini görüyoruz. Hash sonrası mod uyguladık (yüzde işareti ile) ve hash sonucunu en fazla 127 olacak şekilde sınırladık. Potansiyel problemler ne olabilir? Hashing mükemmel değildir, çarpışma (collision) olması mümkündür yani nadiren farklı kelimelerin aynı numaraya eşlenebilmesi durumu. Bu problemleri iyi bir anahtarlama algoritması kullanarak, mod edilen sayıyı büyük tutarak çözmek mümkündür, ya da bu tür nadir çarpışmalar "kabul edilir hata" olarak addedilebilir.
Pandas kullanarak bir Dataframe'i otomatik olarak anahtarlamak istersek,
import pandas as pd
data = {'state': ['Ohio', 'Ohio', 'Ohio', 'Nevada', 'Nevada'],
'year': [2000, 2001, 2002, 2001, 2002],
'pop': [1.5, 1.7, 3.6, 2.4, 2.9]}
data = pd.DataFrame(data)
print data
pop state year
0 1.5 Ohio 2000
1 1.7 Ohio 2001
2 3.6 Ohio 2002
3 2.4 Nevada 2001
4 2.9 Nevada 2002
Şimdi bu veri üzerinde sadece eyalet (state) için bir anahtarlama numarası yapalım
def hash_col(df,col,N):
for i in range(N): df[col + '_' + str(i)] = 0.0
df[col + '_hash'] = df.apply(lambda x: hash(x[col]) % N,axis=1)
for i in range(N):
idx = df[df[col + '_hash'] == i].index
df.ix[idx,'%s_%d' % (col,i)] = 1.0
df = df.drop([col, col + '_hash'], axis=1)
return df
print hash_col(data,'state',4)
pop year state_0 state_1 state_2 state_3
0 1.5 2000 0.0 0.0 0.0 0.0
1 1.7 2001 0.0 0.0 0.0 0.0
2 3.6 2002 0.0 0.0 0.0 0.0
3 2.4 2001 0.0 0.0 0.0 1.0
4 2.9 2002 0.0 0.0 0.0 1.0
Baştan Seyrek Matris ile Çalışmak
Büyük Veri ortamında, eğer kategorik değerler milyonları buluyorsa, o zaman üstteki gibi normal Numpy matrisinden seyreğe geçiş yapmak bile külfetli olabilir. Bu durumlarda daha en baştan seyrek matris üretiyor olmalıyız. Mevcut tüm değerleri önceden bildiğimizi farz edersek,
import numpy as np
import pandas as pd, os
import scipy.sparse as sps
import itertools
def one_hot_column(df, cols, vocabs):
mats = []; df2 = df.drop(cols,axis=1)
mats.append(sps.lil_matrix(np.array(df2)))
for i,col in enumerate(cols):
mat = sps.lil_matrix((len(df), len(vocabs[i])))
for j,val in enumerate(np.array(df[col])):
mat[j,vocabs[i][val]] = 1.
mats.append(mat)
res = sps.hstack(mats)
return res
data = {'state': ['Ohio', 'Ohio', 'Ohio', 'Nevada', 'Nevada'],
'year': ['2000', '2001', '2002', '2001', '2002'],
'pop': [1.5, 1.7, 3.6, 2.4, 2.9]}
df = pd.DataFrame(data)
print df
vocabs = []
vals = ['Ohio','Nevada']
vocabs.append(dict(itertools.izip(vals,range(len(vals)))))
vals = ['2000','2001','2002']
vocabs.append(dict(itertools.izip(vals,range(len(vals)))))
print vocabs
print one_hot_column(df, ['state','year'], vocabs).todense()
pop state year
0 1.5 Ohio 2000
1 1.7 Ohio 2001
2 3.6 Ohio 2002
3 2.4 Nevada 2001
4 2.9 Nevada 2002
[{'Ohio': 0, 'Nevada': 1}, {'2002': 2, '2000': 0, '2001': 1}]
[[ 1.5 1. 0. 1. 0. 0. ]
[ 1.7 1. 0. 0. 1. 0. ]
[ 3.6 1. 0. 0. 0. 1. ]
[ 2.4 0. 1. 0. 1. 0. ]
[ 2.9 0. 1. 0. 0. 1. ]]
one_hot_column çağrısına bir "sözlükler listesi" verdik, sözlük her
kolon için o kolonlardaki mümkün tüm değerleri bir sıra sayısı ile
eşliyor. Sözlük listesinin sırası kolon sırasına uyuyor olmalı.
Niye sözlük verdik? Bunun sebebi eğer azar azar (incremental) ortamda iş yapıyorsak, ki Büyük Veri (Big Data) ortamında her zaman azar azar yapay öğrenim yapmaya mecburuz, o zaman bir kategorik kolonun mevcut tüm değerlerine azar azar ulaşamazdık (verinin başında isek, en sonundaki bir kategorik değeri nasıl görelim ki?). Fakat önceden bu listeyi başka yollarla elde etmişsek, o zaman her öne-hot işlemine onu parametre olarak geçiyoruz.
Sözlük niye one_hot_dataframe çağrısı dışında yaratıldı? Bu çağrı
düz bir liste alıp oradaki değerleri sırayla bir sayıyla eşleyerek her
seferinde bir sözlük yaratabilirdi. Bunu yapmadık, çünkü sözlük yaratımının
sadece bir kere, one_hot_dataframe dışında olmasını istiyoruz. Yine
Büyük Veri ortamını düşünenelim, eşleme (map) için mesela bir script
yazdık, bu script içinde (basında) hemen sözlükler yaratılırdı. Daha sonra
verinin tamamı için, azar azar sürekli one_hot_dataframe çağrısı
yapılacaktır. O zaman arka arkaya sürekli aynı veriyi (sözlükleri) sıfırdan
tekrar yaratmamız gerekirdi. Bu gereksiz performans kaybı demek
olacaktı. Unutmayalım, Büyük Veri ortamında tek bir kategorik kolonun
milyonlarca değişik değeri olabilir!
Azar Azar İşlemek (Incremental, Minibatch Processing)
Çoğu zaman onlarca kategori, birkaç milyonluk satır içeren bir veriye bakmamız gerekiyor; biliyoruz ki bu kadar veri için Büyük Veri teknolojilerine (mesela Spark, Hadoop gibi) geçmek gereğinden fazla külfet getirecek, elimizdeki dizüstü, masaüstü bilgisayarı bu işlemler için yeterli olmalı, fakat çoğu kütüphane tek makinada azar azar işlem yapmak için yazılmamış. Mesela üstte görülen anahtarlama yöntemi anahtarlama başlamadan önce tüm verinin hafızaya alınmasını gerektiriyor.
Bu durumda kendimiz çok basit Python kavramlarını, iyi bir anahtarlama kodunu, ve lineer cebir hesaplarında seyreklik (sparsity) tekniklerini kullanarak ufak veri parçaları işleyen bir ortamı yaratabiliriz.
Örnek veri olarak [4] yazısında görülen oy kalıpları verisini biraz değiştirerek yeni bir analiz için kullanalım. Veri oy verenlerin ırk, cinsiyet, meslek, hangi partiye oy verdikleri ve kazançlarını kaydetmiş, biz analizimizde bahsedilen kategorilerin bu kişilerin kazancıyla bağlantılı olup olmadığına bakacağız. Veriyi oluşturalım,
import pandas as pd
df = pd.read_csv('../stat_logit/nes.dat',sep=r'\s+')
df = df[['presvote','year','gender','income','race','occup1']]
df = df.dropna()
df.to_csv('nes2.csv',index=None)
Önce kategorilerden ne kadar var, sayalım. Basit toplam yani,
import pandas as pd
df = pd.read_csv('nes2.csv')
print u'tüm veri', len(df)
print 'cinsiyet', np.array(df['gender'].value_counts())
print u'ırk', np.array(df['race'].value_counts())
print 'parti', np.array(df['presvote'].value_counts())
print u'kazanç', df['income'].mean()
tüm veri 13804
cinsiyet [7461 6343]
ırk [12075 1148 299 180 85 17]
parti [6998 6535 271]
kazanç 3.07649956534
Mesela son sonuçtaki her hücre belli bir partiye verilen oyların sayısı; veriye göre üç farklı kategori varmış demek ki, veri ABD için olduğuna göre bunlardan ilk ikisi bilinen iki büyük parti, üçüncü hücre de herhalde bağımsız adaylar.
Kazanç 1 ile 5 arasında tam sayılar (1 az, 5 çok) bu sayıları kategorik olarak kabul edip aslında çok çıktılı bir sınıflayıcı eğitmeyi de seçebilirdik, fakat bu örnek için bu sayıları reel hedef olarak aldık: test verisinde tahminleri bakılırsa 2.5'lük kazanç tahminleri görülebilir, bu yüzden.
Kategorik verileri ikileştirmeye gelelim. Burada üç nokta önemli, veriyi azar azar işleyeceğiz demiştik, ve veriyi seyrek matris olarak almak istiyoruz, ve hangi kategorik değerin hangi kolona eşleneceğini elle tanımlamak istemiyoruz (eşleme otomatik olmalı). Seyreklik önemli çünkü eğer 1000 farklı kategorik değere sahip olan 10 tane kolon varsa, bu 10000 tane yeni kolon yaratılması demektir - her farklı kategori için o değere tekabül eden kolon 1 olacak gerisi 0 olacak. Bu rakamlar orta ölçekte bile rahatlıkla milyonlara ulaşabilir. Eğer ikileştirme için seyrek matris kullanırsak çoğu sıfır olan değerler hafızada bile tutulmaz. Eşleme otomatik olmalı, zaten onun için anahtarlama yapacağız.
Anahtarlama icin sklearn.feature_extraction.text.HashingVectorizer
var,
from sklearn.feature_extraction.text import HashingVectorizer
import numpy as np
vect = HashingVectorizer(n_features=20)
a = ['aa','bb','cc']
res = vect.transform(a)
print res
(0, 5) 1.0
(1, 19) 1.0
(2, 18) -1.0
Sonuçlar seyrek matris olarak, ve üç değer için üç ayrı satır olarak geldi. Anahtarlama niye bazen -1 bazen +1 veriyor? Aslında bu bizim için çok faydalı, çünkü birazdan PCA işleteceğiz, ve PCA her veri kolonunun sıfırda ortalanmış olmasını ister. Üstteki teknikte anahtar üreten fonksiyon -1,+1 arasında rasgele seçim yapıyor gibi duruyor, bize göre bu üretilen anahtar kolonlarında -1, +1 değerlerinin doğal olarak dengelenmesi için yapılmış, böylece otomatik olarak ortalamaları sıfıra inecektir. Akıllıca bir teknik.
Devam edelim, sonucu tek satır olacak şekilde kendimiz tekrar
düzenleyebiliriz. O zaman Python yield kavramını [3] kullanarak
(azar azar satır okumak için), anahtarlama, ve seyrek matrisler ile şu
şekilde bir kod olabilir,
from sklearn.feature_extraction.text import HashingVectorizer
import numpy as np
import pandas as pd, csv
import scipy.sparse as sps
HASH = 30
vect = HashingVectorizer(decode_error='ignore',n_features=HASH)
def get_row(cols):
with open("nes2.csv", 'r') as csvfile:
rd = csv.reader(csvfile)
headers = {k: v for v, k in enumerate(next(rd))}
for row in rd:
label = float(row[headers['income']])
rrow = [x + str(row[headers[x]]) for x in headers if x in cols]
X_train = vect.transform(rrow)
yield X_train.tocoo(), label
def get_minibatch(row_getter,size=10):
X_train = sps.lil_matrix((size,HASH))
y_train = []
for i in range(size):
cx,y = row_getter.next()
for dummy,j,val in zip(cx.row, cx.col, cx.data): X_train[i,j] = val
y_train.append(y)
return X_train, y_train
# tek bir satir goster
cols = ['gender','income','race','occup1']
row_getter = get_row(cols)
X,y = get_minibatch(row_getter,size=1)
print y, X.todense()
[4.0] [[ 0. 0. 0. -1. 0. 0. 0. 0. 0. 0. 0. 0. 1. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0. 0. 1. 0. 0. 1. 0.]]
İlgilendiğimiz kolon listesini get_row'a verip bir gezici fonksiyon
yarattık. Bu geziciyi get_minibatch'e verdik, kaç tane satır
istediğimizi ona söylüyoruz, o bize istenen kadar satırı arka planda
geziciye sorarak seyrek matris olarak veriyor. 10 tane daha isteyelim,
X,y = get_minibatch(row_getter,size=10)
print len(y), X.shape, type(X)
10 (10, 30) <class 'scipy.sparse.lil.lil_matrix'>
PCA
Lineer Cebir'in temel bileşen analizi (PCA) tekniğini kullanarak boyut azaltması yapabiliriz. Veriyi yine satır satır işleyerek PCA hesabı yapan teknikler var, kod veriyi seyrek formatta da alabiliyor. Bu kod lineer cebir PCA yazısında işlendi.
import sys; sys.path.append('../stat_170_pca')
import ccipca
cols = ['gender','income','race','occup1']
row_getter = get_row(cols)
pca = ccipca.CCIPCA(n_components=10,n_features=30)
for i in range(10000):
X,y = get_minibatch(row_getter,size=1)
pca.partial_fit(X)
pca.post_process()
print 'varyans orani'
print pca.explained_variance_ratio_
varyans orani
[ 0.36086926 0.16186391 0.13377998 0.09440711 0.0702763 0.05113956
0.04768294 0.0343724 0.02336052 0.02224802]
Her bileşenin verideki varyansın ne kadarını açıkladığı görülüyor.
Peki 30 kolonu 10 kolona indirdik, acaba veri temsilinde, tahmin etmek amacında ilerleme elde ettik mi? Veriyi PCA'nın bulduğu uzaya yansıtıp bu boyutu azaltılmış veriyi regresyonda kullansak ne olur acaba? Yansıtma ve regresyon,
from sklearn.linear_model import SGDRegressor
clf = SGDRegressor(random_state=1, n_iter=1)
row_getter = get_row(cols)
P = pca.components_.T
for i in range(10000):
X_train, y_train = get_minibatch(row_getter,1)
Xp = np.dot((X_train-pca.mean_),P)
clf.partial_fit(Xp, y_train)
Şimdi sonraki 1000 satırı test için kullanalım,
y_predict = []
y_real = []
for i in range(1000):
X_test,y_test = get_minibatch(row_getter,1)
Xp = np.dot((X_test-pca.mean_),P)
y_predict.append(clf.predict(Xp)[0])
y_real.append(y_test[0])
y_predict = np.array(y_predict)
y_real = np.array(y_real)
err = np.sqrt(((y_predict-y_real)**2).sum()) / len(y_predict)
print 'ortalama tahmin hatasi', err
print 'maksimum deger', np.max(y_real)
ortalama tahmin hatasi 0.0105872845541
maksimum deger 5.0
1 ile 5 arasında gidip gelen değerlerin tahmininde 0.01 civarı ortalama hata var. Fena değil. Peki verinin kendisini olduğu gibi alıp regresyonda kullansaydık? Hedef verisi kazanç, kaynak kolonları geri kalan kategoriler. Üstte olduğu gibi veri parçaları 1000'er satır, 10 parça olarak alacağız, yani 10,000 satır modeli eğitmek için kullanılacak. Geri kalanlar test verisi olacak.
sklearn.linear_model.SGDRegressor ufak seyrek matris parçaları ile
eğitilebiliyor,
from sklearn.linear_model import SGDRegressor
clf = SGDRegressor(random_state=1, n_iter=1)
row_getter = get_row(cols)
y_predict = []; y_real = []
for i in range(10):
X_train, y_train = get_minibatch(row_getter,1000)
clf.partial_fit(X_train, y_train)
X_test,y_test = get_minibatch(row_getter,1000)
y_predict = clf.predict(X_test)
err = np.sqrt(((y_predict-y_test)**2).sum()) / len(y_predict)
print 'ortalama tahmin hatasi',
ortalama tahmin hatasi 0.0208096951078
Bu sonuç ta hiç fena değil. Sonuç olarak veri içinde bazı kalıplar olduğunu gördük, tahmin yapabiliyoruz. Hangi kolonların daha önemli olduğunu bulmak için her kolonu teker teker atıp hatanın yukarı mı aşağı mı indiğine bakabilirdik.
Tekrar vurgulamak gerekirse: üstteki analizde aslında çok fazla kategorik
veri yok, yani statsmodels.formula.api üzerinden güzel formüllerle,
regresyon çıktısında her kategorik değerin güzelce listelendiği türden bir
kullanıma da gidebilirdik. Bu yazıda göstermeye çalıştığımız çok fazla
veri, çok fazla kolon / kategori olduğunda ve tek makina ortamında takip
edilebilecek çözümler.
Zaman Karşılaştırmak
Eğer 23:50 ile sabah 00:10 zamanını karşılaştırmak istersek ne yaparız? Eğer saat ve dakika farkını direk hesaplasak bu iki zamanın çok uzak olduğunu düşünebilirdik. Fakat aslında aralarında 20 dakika var, zaman dönüp başa gelen bir kavram.
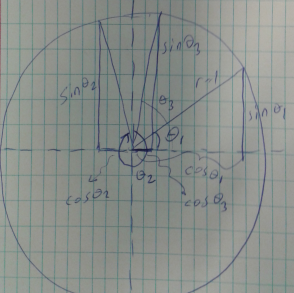
Bu hesabı yapmak için bir yöntem çember, açılar kullanmak. Gün içindeki zamanı 0 ile 1 arasında kodlarız, sonra bu büyüklüğü $2\pi$ ile çarparız, bu bize çember üzerindeki bir noktayı verir, yani zamanı açıya çevirmiş oluruz. Sonra açının $\sin$, $\cos$ değerini hesaplayıp iki rakam elde ederiz, bu iki sayı bize gün içindeki zamanı temsil eden bir büyüklük verir.
Bu büyüklükleri birbirleri ile karşılaştırmak daha kolay, üstteki şekilde $\theta_2$ ve $\theta_3$ birbirine yakın, karşılaştırma yaparken $\sin$ bize dikey eksendeki izdüşümü, $\cos$ yatay eksendeki izdüşümünü verir, $\theta_2,\theta_3$ için y eksenindeki yansıma birbirine çok yakın. Eksen x üzerindeki yansıma farklı biri eksi biri artı yönde fakat yine de mutlak değer bağlamında birbirlerine çok yakınlar. İstediğimiz de bu zaten.
import scipy.linalg as lin
t1 = 0.12 * 2*np.pi
t2 = 0.97 * 2*np.pi
t3 = 0.03 * 2*np.pi
d1 = (np.cos(t1), np.sin(t1))
d2 = (np.cos(t2), np.sin(t2))
d3 = (np.cos(t3), np.sin(t3))
print ("%f %f" % d1)
print ("%f %f" % d2)
print ("%f %f" % d3)
print u'uzaklık 1-2 =', lin.norm(np.array(d1)-np.array(d2))
print u'uzaklık 2-3 =', lin.norm(np.array(d2)-np.array(d3))
0.728969 0.684547
0.982287 -0.187381
0.982287 0.187381
uzaklık 1-2 = 0.907980999479
uzaklık 2-3 = 0.374762629171
Kaynaklar
[1] Teetor, R Cookbook
[2] Scikit-Learn Documentation, 4.2. Feature extraction, http://scikit-learn.org/dev/modules/feature_extraction.html
[3] Bayramlı, Fonksiyon Gezmek ve Yield, https://burakbayramli.github.io/dersblog/sk/2011/02/fonksiyon-gezmek-ve-yield.html
[4] Bayramlı, Istatistik, Lineer Regresyon
Yukarı