Lineer Regresyon
Bir hedef değişkeninin bir veya daha fazla kaynak değişkenine olan bağlantısını bulmak için en basit yöntemlerden biri bu ilişkinin lineer olduğunu kabul etmektir, yani eldeki değişkenlerin belli ağırlıklar ile çarpımının toplamı olarak. İlk başta bilinmeyen bu ağırlıkları, ya da katsayıları bulmak için En Az Kareler (Least Squares) en iyi bilinen yöntemlerden biri; En Az Kareler daha önce pek çok değişik ders notlarında, yazıda türetildi. Mesela [7], [8], ya da [9].
Lineer Regresyonun sadece iki değişken temelli işlemek gerekirse,
$$ Y = \beta_0 + \beta_1 x + \epsilon$$
olabilir. Eğer iki değişkenden fazlası var ise bu bir düzlem uydurulacak demektir. Değişken $\epsilon$, $N(0,\sigma^2)$ dağılımından gelen hatadır ve $\sigma$ bilinmez. Eğer veriyi $(x_1,y_1),...(x_n,y_n)$ ikili olarak grafiklesek
gibi gözükebilirdi, lineer regresyon ile yapmaya çalıştığımız tüm noktalara olabilecek en yakın düz çizgiyi (üstte görüldüğü gibi) bulmaktır.
Bu düz çizgiyi (ki boyutlu ortamda bu çizgi bir hiper düzlem olurdu, $\beta_2,\beta_3,..$ gibi daha fazla katsayı gerekirdi), En Az Kareler ile bulduktan sonra elimize geçenler katsayı değerlerinin tahminidir, ki bunlar bazı kaynaklarda $\hat{\beta}_0,\hat{\beta}_1$ olarak tanımlanır, bu notasyon istatistikteki "tahmin edici (estimator)" notasyon ile uyumlu. Bu tahmin ediciler ile elde edilen $y$'nin kendisi de bir tahmin edici haline gelir ve bir düz çizgiyi tanımlar,
$$ \hat{y} = \hat{\beta}_0 + \hat{\beta}_1x $$
Katsayıların tahmin edicilerinin de dağılımı vardır ve bu dağılım, ideal şartlarda bir normal dağılımdır. İspat için bu yazının sonuna bakınız.
Örnek olarak lineer regresyon için tarihte kullanılan neredeyse ilk veri setini seçeceğim. Bu veri çocukların ve onların ebeveynlerinin boy uzunluğunu içeren Galton'un 19. yüzyılda analiz ettiği veri setidir. Hatta öyle ki regresyon kelimesinin bile bu problem ile alakası var, İngilizce regress kelimesi baştaki (çoğunlukla daha iyi olmayan) bir hale dönmek anlamında kullanılır, ve problemde çocukların boyunun ebeveyn boyuna "geri döndüğü" ya da ondan ne kadar etkilendiği incelenmektedir.
import pandas as pd
df = pd.read_csv('galton.csv',sep=',')
print df.head(4)
child parent
0 61.7 70.5
1 61.7 68.5
2 61.7 65.5
3 61.7 64.5
Şimdi regresyonu işletelim, sadece bağımsız tek değişken olacak, ebeveyn
boyu parent, hedef değişken ise çocuk child içinde.
import statsmodels.formula.api as smf
results = smf.ols('child ~ parent', data=df).fit()
print results.summary()
OLS Regression Results
==============================================================================
Dep. Variable: child R-squared: 0.210
Model: OLS Adj. R-squared: 0.210
Method: Least Squares F-statistic: 246.8
Date: Thu, 03 Nov 2016 Prob (F-statistic): 1.73e-49
Time: 09:11:04 Log-Likelihood: -2063.6
No. Observations: 928 AIC: 4131.
Df Residuals: 926 BIC: 4141.
Df Model: 1
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [95.0% Conf. Int.]
------------------------------------------------------------------------------
Intercept 23.9415 2.811 8.517 0.000 18.425 29.458
parent 0.6463 0.041 15.711 0.000 0.566 0.727
==============================================================================
Omnibus: 11.057 Durbin-Watson: 0.046
Prob(Omnibus): 0.004 Jarque-Bera (JB): 10.944
Skew: -0.241 Prob(JB): 0.00420
Kurtosis: 2.775 Cond. No. 2.61e+03
==============================================================================
Warnings:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
[2] The condition number is large, 2.61e+03. This might indicate that there are
strong multicollinearity or other numerical problems.
print pd.Series(results.resid).describe()
count 9.280000e+02
mean 4.484995e-13
std 2.237339e+00
min -7.805016e+00
25% -1.366144e+00
50% 4.869321e-02
75% 1.633856e+00
max 5.926437e+00
dtype: float64
Bu çıktıda gösterilenler ne anlama gelir?
1) coef altında görülen değerler sırasıyla $\beta_o,\beta_1$
tahminleridir, yani $\hat{\beta}_o,\hat{\beta}_1$. Bunlar bulmak istediğimiz
katsayılar. İki boyutta olduğumuz için düz bir çizgiden bahsediyoruz, bu
çizginin $y$ eksenini kestiği yer kesi (intercept) $\hat{\beta}_0$'da ve ebeyne
(parent) tekabül eden katsayı $\hat{\beta}_1$.
Teorik olarak eğer bir katsayı sıfır ise bu işe yaramaz bir katsayıdır, çünkü modele hiçbir şey "eklemez". Fakat Basit En Az Kareler (ordinary least squares -OLS-)'in hesapladığı bir tahmindir nihayetinde ve hiçbir zaman sıfır olmayacaktır. O zaman soruyu biraz daha değiştirmek gerekir: istatistiki olarak düşünürsek gerçek katsayının sıfır olma olasılığı nedir? Katsayı yanında görülen $t$ ve $P>|t|$ (diğer ismiyle p-değeri) bunun için kullanılır.
$t$ değeri bir katsayı için onun tahminini ve standart hatasına bölerek elde edilir. Üstteki çıktıda mesela 23.9415/2.811=8.517. Bu değer katsayı tahmininin veriden veriye ne kadar değişik sonuçlar verebileceğini (variability) gösterir, ve bir bakıma bu katsayı tahmininin kesinliği (precision) hakkında bir rapordur. Eğer bir katsayı tahmini, standart hatasına göre büyük ise (ki bölüm bunu gösterir) bu katsayının sıfır olmadığına dair güçlü bir işaret olarak alınabilir.
Peki ne kadar büyük bir sayı büyük sayılmalıdır? Bunun için p-değerine başvuruyoruz. P-değerini hesaplamak için t değeri ve standart hatasının dağılımından bahsetmek lazım.
t değeri bir rasgele değişken olduğu için bir dağılımı vardır, ve bu dağılım Öğrenci t (Student t) dağılımıdır. Sebep şu, t değerinin kendisi de iki rasgele değişkeninin bölümüdür, bu değişkenlerden biri katsayının kendisidir, ki bu değer nüfustaki "gerçek" katsayı etrafında normal olarak dağılmış bir rasgele değişken olarak kabul edilir. Diğeri ise, yani bölen, tahmin edici $S$'tır ki bir chi kare rasgele değişkenin kareköküdür. Bu bölümün Öğrenci t dağılımına sahip olduğu daha önce gösterildi.
Standart hata ise, artık / kalıntı değerlerle (residuals) alakalıdır
(results.resid içinde), ve bu değerler model uydurulduktan sonra o modeli
kullanarak gerçek veriye ne kadar uzak düştüğümüzü gösterir. Formül olarak her
veri noktası $i$ için $r_i = y_i - \beta_1x_i - \beta_o$. Her katsayı için de
ayrı ayrı kalıntı hesaplanabilir.
İdeal durumda, yani modelin doğru, veriye uyduğu durumda artıkların mükemmel bir Normal dağılıma sahip olması gerekir, çünkü veri içindeki tüm örüntü, kalıp model tarafından "bulunmuştur" ve geri kalanlar gürültüdür (gürültü tabii ki Normal dağılımda). İdeal ortamda OLS algoritmasının, matematiksel olarak, ortalaması (mean) sıfır olan artıklar üretmesi garantidir. Bir diğer varsayım uyduralan değişkenlerin katsayılarının onların "gerçek" değerleri etrafında merkezlenen bir Normal dağılıma sahip olduğudur (ispat için [10] yazısının sonuna bakılabilir). Bu normallik önemli çünkü katsayı tahmini ile standart hatayı bölünce başka bir Öğrenci t dağılımı ortaya çıkacak.
Kalıntıların normalliği QQ grafiği ile kontrol edilebilir, bkz [11],
import statsmodels.api as sm
sm.qqplot(results.resid)
plt.savefig('stat_linreg_01.png')
Oldukça düz bir çizgi, uyum başarılı demek ki..
Şimdi, katsayı için olan kalıntı değerlerinin karesini alıp toplarsak ve karekökü alırsak, bu rasgele değişkenin Chi Kare (Chi Square) olarak dağıldığı bilinir, ve yine bilinir ki standart normal rasgele değişken, bolu, chi kare karekökü bize bir Öğrenci t dağılımını verir, mesela
$$ t = \frac{Z}{\sqrt{V / m}} = t_m$$
serbestlik derecesi $m$ olan bir Öğrenci t rasgele değişkenidir.
Öğrenci t'den p-değeri üretmek için t değerinin sıfırdan ne kadar uzağa düştüğü bir Öğrenci t olasılık hesabına dönüştürülür. Önce katsayının tam değeri (absolute value) alınır, eksileri artı yaparız, çünkü sıfırdan uzaklık ile ilgileniyoruz sadece ve Öğrenci t dağılımı simetriktir, sonra bu değer $t_m$ dağılımı üzerinden bir olasılık hesabına dönüştürülür. Yani "katsayı / standart hata bir $t_m$ ile dağılmış ise, elde edilen bölümün o dağılımdan gelme olasılığı nedir?" gibi bir soru. Olasılık hesabı yoğunluk fonksiyonu üzerinde bir alan hesabıdır, t değeri 2 ise ve $t_5$ için bu alan hesabı şöyle,
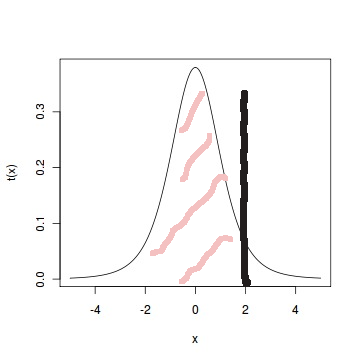
Ayrıca bu olasılık sonucu sıfır ile karşılaştırmak kolay olsun diye 1'den çıkartılır ve 2 ile çarpılır, istatistiğin böylece iki taraflı (two-sided) olduğu belirtilir. $m$, veri nokta sayısı, eksi katsayı sayısı, artı bir olarak hesaplanıyor. Eğer sonuç 0.05'ten küçük ise bu iyiye işarettir, 0.05'ten büyük olan değerler iyi değildir. Galton örneğinde $\hat{\beta_0}$ için,
from scipy.stats import t
print 2*(1-t(927).cdf(np.abs(8.517)))
0.0
Üstteki sonuç 0.0 değeri çok iyi. Demek ki bu katsayı önemli (significant).
2) Artıklarda sıfırdan sapma, herhangi bir yöne doğru yamukluk (skew) OLS
uyumsuzluğunun işareti olabilir, üstte artıklar üzerinde describe
çağrısı ile medyanı (\%50 noktası) hesaplattık, bu değerin 0.04 ile sıfırdan
çok az sağa doğru saptığını görüyoruz. \%25, \%75 bölgelerinin işaretlerine
bakmadan tam (absolute) değerlerine bakalım, 1.36 ve 1.63, çok az
farklılar. İdealde hiç fark olmamasını isteriz çünkü normal dağılım
simetriktir, her iki tarafında da bu bölgelerin yakın değerde olmasını
bekleriz. Fakat bu değerler alarm yaratacak nitelikte değil.
Artıkların minimum, maksimum (min,max) değerleri verideki ekstrem, aykırı
değerlere (outlier) dair bir işaret olabilir.
3) $R^2$, ya da R-squared, modelin kalitesiyle alakalıdır, ne kadar
büyükse o kadar iyidir. Matematiksel olarak bu değer $y$'nin değişiminin /
varyansının oran olarak ne kadarının regresyon modeli tarafından
"açıklanabildiğini" belirtir. Üstteki örnekte $R^2=0.21$ ise model varyansın
yüzde 21'ini açıklıyor. Ya da "bir çocuğun boyunun yüzde 21'i ebeveyn boyu ile
açıklanabilir" sözü de söylenebilir. Geri kalan 0.75'lik yani yüzde 75'lik
"açıklanamayan" kısmın değişik sebepleri olabilir; belki hesaba katmadığımız
değişkenler vardır, ya da örnekleme prosedüründe hatalar yapılmıştır, ya da
lineerlik bu probleme uygun değildir, vs.
Tavsiyemiz düz $R^2$ yerine OLS çıktısında görülen "düzeltilmiş $R^2$" yani
Adj. R-squared bilgisinin kullanılmasıdır, çünkü bu bilgi modeldeki
değişken sayısını da hesaba katar ve daha iyi bir ölçüttür.
4) F istatistiği: Bu istatistik tüm modelin önemli mi önemsiz mi olduğunu irdeler. Eğer modelde sıfır olmayan en az bir katsayı var ise model önemlidir (herhangi bir $i$ için $\beta_i \ne 0$). Eğer tüm katsayılar sıfır ise model önemsizdir ($\beta_0=\beta_1,\dots,\beta_n=0$). Örnekte
... F-statistic: 246.8
... Prob (F-statistic): 1.73e-49
Prob (F-statistic) bir p-değeri, ve bu değer 0.05'ten küçük ise model
büyük bir ihtimalle önemlidir, eğer 0.05'ten büyük ise büyük ihtimalle önemli
değildir. Üstteki p-değeri 1.73e-49 gösteriyor, çok ufak bir değer, yani bu iyi.
Not: Çoğu kişi OLS çıktısında ilk önce $R^2$'ye bakar, fakat bilgili istatistikçi F'e bakar, çünkü bir model önemli değilse, geri kalan hiçbir ölçütün önemi yoktur.
Nihai analiz olarak bu veride parent katsayısının pozitif olan değerine
bakarak çocuk ve ebeveyn boyu arasında bir bağlantı olduğunu söyleyebiliriz.
Basamaklı Regresyon (Stepwise Regression)
Eğer elimizde çok fazla değişken var ise, bu değişkenlerden hangilerinin en iyi olduğunu seçmek oldukça zor olabilir. Önemlilik sayıları burada biraz yardımcı olabilir, fakat değişkenlerin eklenip, çıkartılması regresyonun tamamını etkilediği için deneme / yanılma ile ekleme / çıkartma işleminin yapılması gerekebilir, ki bu işlemi elle yapmak külfetli olur. Acaba bu yöntemi otomize edemez miyiz?
R dilindeki lm'in step adlı özelliği burada yardımcı
olabilir. Önce yapay bir veri üretelim,
import pandas as pd
n = 100
df = pd.DataFrame()
np.random.seed(10)
df['x1'] = np.random.normal(size=n)
df['x2'] = np.random.normal(size=n)
df['x3'] = np.random.normal(size=n)
df['x4'] = np.random.normal(size=n)
df['y'] = 10 + -100*df['x1'] + 75*df['x3'] + np.random.normal(size=n)
Yapay veride farkedileceği üzere x2,x4 modele eklenmedi bile. Bu
değişkenler önemsiz, ürettiğimiz için biz bunu biliyoruz. Bakalım regresyon bunu
keşfedecek mi? Şimdi tüm değişkenlerle bir OLS yapalım,
%load_ext rpy2.ipython
%R -i df
%R fullmodel <- lm(y~x1+x2+x3+x4,data=df)
%R -o res res = summary(fullmodel)
print res
Call:
lm(formula = y ~ x1 + x2 + x3 + x4, data = df)
Residuals:
Min 1Q Median 3Q Max
-3.15789 -0.63251 -0.01537 0.58051 2.30127
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 9.94953 0.09378 106.098 <2e-16 ***
x1 -99.95333 0.09686 -1031.975 <2e-16 ***
x2 -0.04103 0.09500 -0.432 0.667
x3 75.14720 0.10240 733.851 <2e-16 ***
x4 0.04863 0.10015 0.486 0.628
---
Residual standard error: 0.9292 on 95 degrees of freedom
Multiple R-squared: 0.9999, Adjusted R-squared: 0.9999
F-statistic: 4.23e+05 on 4 and 95 DF, p-value: < 2.2e-16
Görüldüğü gibi daha baştan x2,x4 önemsiz bulundu. Ama daha karmaşık bir
modelde bu o kadar rahat bulunmayabilirdi. Şimdi step ile tam modelden bu
değişkenler çekip çıkartılabiliyor mu ona bakacağız.
R dilinde basamaklı regresyon iki şekilde işler. Ya tam modelden geriye gidersiniz yani tam modelden ise yaramayan değişkenleri atarsınız, ya da en baz (boş) modelden başlayıp ileri gidersiniz yani ekleye ekleye en iyi değişkenlere erişmeye uğraşırsınız. İlk önce eliminasyonu görelim,
%R reducedmodel <- step(fullmodel, direction="backward")
%R -o resred resred<-summary(reducedmodel)
print resred
Call:
lm(formula = y ~ x1 + x3, data = df)
Residuals:
Min 1Q Median 3Q Max
-3.1667 -0.6078 -0.0256 0.5732 2.3592
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 9.95039 0.09251 107.6 <2e-16 ***
x1 -99.95181 0.09540 -1047.7 <2e-16 ***
x3 75.14514 0.10101 744.0 <2e-16 ***
---
Residual standard error: 0.9217 on 97 degrees of freedom
Multiple R-squared: 0.9999, Adjusted R-squared: 0.9999
F-statistic: 8.599e+05 on 2 and 97 DF, p-value: < 2.2e-16
Doğru sonuçlar bulundu. Bu yöntem fena değildir, ama bazen o kadar çok değişken
vardır ki tam modelle başlamak iyi bir fikir olmayabilir, o zaman boş başlayıp
ileri gitmek daha mantıklı olabilir. Boş modelde sadece y ~ 1 olacak,
biraz garip gelebilir, çünkü hiç değişken yok (ki bu durumda uydurulan tüm
değişkenler sadece $y$'nin ortalamasıdır). Neyse, ileri giden modelde
step'e hangi değişkenlerin aday / potansiyel değişken olduğunu belirtmek
gerekir, bunu scope ile yaparız,
%R minmodel <- lm(y ~ 1,data=df)
%R fwd <- step(minmodel, direction="forward", scope = ( ~ x1 + x2 + x3 + x4))
%R -o fwdres fwdres <- summary(fwd)
print fwdres
Call:
lm(formula = y ~ x1 + x3, data = df)
Residuals:
Min 1Q Median 3Q Max
-3.1667 -0.6078 -0.0256 0.5732 2.3592
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 9.95039 0.09251 107.6 <2e-16 ***
x1 -99.95181 0.09540 -1047.7 <2e-16 ***
x3 75.14514 0.10101 744.0 <2e-16 ***
---
Residual standard error: 0.9217 on 97 degrees of freedom
Multiple R-squared: 0.9999, Adjusted R-squared: 0.9999
F-statistic: 8.599e+05 on 2 and 97 DF, p-value: < 2.2e-16
Yine aynı sonuca geldik. Tabii bu çok basit bir yapay veri, o yüzden aynı yere gelmiş olmamız şaşırtıcı değil. Gerçek problemlerde geriye ve ileri giden modellerin ikisini de deneyip sonuçları karşılaştırmak iyi oluyor. Sonuçlar şaşırtıcı olabilir.
Bir diğer tavsiye basamaklı regresyonu her derda deva bir yöntem olarak görmemek, çünkü üstteki çıktılara göre sihirli bir şekilde en kullanışlı alt kümeyi buluveriyor, vs, fakat bu metot, değişkenleri iyi tanıyan birisi tarafından dikkatli bir şekilde alt kümenin elenip, seçilerek bulunması yerine geçemez. Bunu özellikle belirtiyoruz, çünkü bazılarının aklına şöyle bir şey gelebilir,
%R full.model <- lm(y ~ (x1 + x2 + x3 + x4)^4)
%R reduced.model <- step(full.model, direction="backward")
Üstte görülen ^4 kullanımı dört değişken arasındaki tüm mümkün
etkileşimleri (interaction) ortaya çıkartır, yani
x1:x2,x1:x2:x3:x4,x3:x4,.. gibi ve bunların tamamını basamaklı
regresyona sokar, çünkü bu cinliğe göre nasılsa eliminasyon metotu ise yaramayan
değişkenleri atacaktır (!). Bu metot iyi işlemeyecektir, çoğu etkileşimin hiçbir
anlamı yoktur, step fonksiyonu herhalde çok fazla seçenek arasında
boğulur, sonuçta elimizde bir sürü ise yaramaz değişken kalacaktır.
Soru
Diyelim ki elimde bir veri seti var ve üzerinde OLS uyguladım, sonuçlara baktım. Eğer bu veri setini alıp, kendisine eklersem, yani veriyi iki katına çıkartırsam, ilk işlettiğim OLS'teki katsayılara, ve standart hataya ne olur?
Cevap
Dikkat, bu soru bir mülakat sorusudur! :) Düşünelim, sezgisel bir şekilde, 2 boyutta, uydurulan tek çizginin altında ve üstünde yine aynı verilerin bir kez daha tekrarlanacağını farkederiz, ki bu çizginin yerini değiştirmezdi. Yani katsayılar aynı kalırdı. Fakat standart sapmaya ne olurdu? Artıklardan başlayalım,
$$ r_i = y_i - \beta_0 + \beta_1x_i $$
Veriyi ikiye katlayınca,
$$ 2y_i - 2\beta_0 + 2\beta_1x_i \Rightarrow 2r_i $$
Standart hata hesabı, kolaylık için $n-1$ yerine $n$, ve $C = r_i^2$,
$$ \sqrt{\frac{\sum_i (2r_i)^2}{2n}} =
\sqrt{\frac{4 \sum_i r_i^2}{2n}} =
\sqrt{\frac{4 C}{2n}}
$$
Eski veri seti için aynı hesap $\sqrt{C/n}$. İki tarafta da karekök var, sadece karekök içine bakalım,
$$
\frac{C}{n} \quad ? \quad \frac{4 C}{2n}
$$
Aradaki ilişki nedir? Eğer veriyi ikiye katlarsak $C$ 4 katına çıkıyor, ama herhangi bir $n > 2$ için, $2n$ bu büyümeyi geçer, ve sağdaki büyüklük soldakina nazaran küçülür.
$$
\frac{C}{n} \quad > \quad \frac{4 C}{2n}, \qquad n>2 \textrm{ için }
$$
Demek ki yeni veri setinde standard hata küçülür. Eğer bu değer küçülürse, katsayılara ait olan standart hatalar da, ki onlar biraraya gelerek standart hatayı oluşturacaklar, küçülecektir. Standart hatanın küçülmesi aslında şaşırtıcı olmamalı, aynı yönde daha fazla veri alınca elimizdeki katsayılarından daha "emin" hale geldik. Bu iyi bir şey olarak görülebilirdi belki, ama bu durumun modelin geri kalanı üzerindeki etkilerini şimdi düşünelim. Eğer katsayı aynı kalır, hata küçülürse katsayı / hata olarak hesaplanan t değeri buyur. Daha büyüyen t değeri daha küçülen p-değeri demektir! Yani veriyi ikiye katlayınca birden bire önemsiz olan ($>0.05$) bir değişken, önemli hale gelebilir. Altta örneğini görüyoruz,
import statsmodels.formula.api as smf
results = smf.ols('y~x1+x2+x3+x4', data=df).fit()
print results.summary()
OLS Regression Results
==============================================================================
Dep. Variable: y R-squared: 1.000
Model: OLS Adj. R-squared: 1.000
Method: Least Squares F-statistic: 4.230e+05
Date: Sat, 14 Mar 2015 Prob (F-statistic): 5.97e-201
Time: 15:56:03 Log-Likelihood: -131.99
No. Observations: 100 AIC: 274.0
Df Residuals: 95 BIC: 287.0
Df Model: 4
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [95.0% Conf. Int.]
------------------------------------------------------------------------------
Intercept 9.9495 0.094 106.098 0.000 9.763 10.136
x1 -99.9533 0.097 -1031.975 0.000 -100.146 -99.761
x2 -0.0410 0.095 -0.432 0.667 -0.230 0.148
x3 75.1472 0.102 733.851 0.000 74.944 75.350
x4 0.0486 0.100 0.486 0.628 -0.150 0.247
==============================================================================
Omnibus: 3.126 Durbin-Watson: 2.267
Prob(Omnibus): 0.210 Jarque-Bera (JB): 2.795
Skew: -0.191 Prob(JB): 0.247
Kurtosis: 3.724 Cond. No. 1.26
==============================================================================
Veriyi ikiye katlayıp bir daha OLS,
df2 = pd.concat((df,df))
results = smf.ols('y~x1+x2+x3+x4', data=df2).fit()
print results.summary()
OLS Regression Results
==============================================================================
Dep. Variable: y R-squared: 1.000
Model: OLS Adj. R-squared: 1.000
Method: Least Squares F-statistic: 8.683e+05
Date: Sat, 14 Mar 2015 Prob (F-statistic): 0.00
Time: 15:56:41 Log-Likelihood: -263.98
No. Observations: 200 AIC: 538.0
Df Residuals: 195 BIC: 554.4
Df Model: 4
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [95.0% Conf. Int.]
Intercept 9.9495 0.065 152.006 0.000 9.820 10.079
x1 -99.9533 0.068 -1478.512 0.000 -100.087 -99.820
x2 -0.0410 0.066 -0.619 0.537 -0.172 0.090
x3 75.1472 0.071 1051.389 0.000 75.006 75.288
x4 0.0486 0.070 0.696 0.487 -0.089 0.186
==============================================================================
Omnibus: 4.922 Durbin-Watson: 2.274
Prob(Omnibus): 0.085 Jarque-Bera (JB): 5.589
Skew: -0.191 Prob(JB): 0.0611
Kurtosis: 3.724 Cond. No. 1.26
==============================================================================
Görüldüğü gibi x4 artık $<0.05$ altında!
OLS'in bu tür nüanslarını bilmek iyi olur. Eğer veride tekrar varsa, herhangi bir sebeple, tekrarlayan verileri çıkartmak belki de mantıklı olacaktır.
ABD Başkanlık Yarışını Tahmin Etmek
ABD başkanlık yarışlarının oldukça tahmin edilebilir olduğu uzunca süredir iddia
edilmektedir. Bu alanda pek çok model var, Andrew Gelman'ın oldukça çetrefil,
MCMC kullanan modelinden [4] (ki bunun için başkasının yazdığı kod [5]'te
bulunabilir), ya da daha öz, basit bir metot [3] mevcuttur. En basit ve etkili
yöntem Değişim Zamanı (Time for Change) modeli, bu modele göre
başkanlık yarışının olduğu Haziran ayı itibariyle ekonomik büyüme yüzdesi
(gdp_growth), mevcut başkanın net destek oranı (net_approval, ki
bu rakam destek yüzdesinden desteklemeyen yüzdesi çıkartılarak hesaplanır) ve o
anki başkanının partisinin, 2 dönem ya da daha fazladır Beyaz Ev'de olup
olmadığı bilgisi 1/0 değeri ile kodlanarak (two_terms) lineer regresyona
verilir ve hedef değişken olarak, yönetimi elinde tutan partinin ülke genelinde
tüm oyların (popular vote) yüzde kaç alacağı tahmin edilmeye uğraşılır.
Örnek olarak Clinton ve Bush I arasındaki 1992 yarısında Cumhuriyetçi adayın
(çünkü o zamanki başkan Cumhuriyetçi) yüzde kaç oy alacağı tahmin edilecek,
two_terms=1 çünkü iki dönem Cumhuriyetçi Reagan ardından bir dönem
Cumhuriyetçi Bush gelmiş, Cumhuriyetçiler uzun süredir baştalar.
Gore / Bush arasındaki 2000 yılı yarısında Demokratların yüzdesini tahmin etmeye uğraşıyoruz, çünkü başta Demokrat Clinton var, ve iki dönemdir orada. Net popülarite ve büyüme hep o anki başkan ve onun partisinin performansı ile alakalı. Bu regresyonu işlettiğimizde, sonuçlar şöyle,
import statsmodels.formula.api as smf
import pandas as pd
df = pd.read_csv('prez.csv')
print df.head() , '\n'
regr = 'incumbent_vote ~ gdp_growth + net_approval + two_terms'
results = smf.ols(regr, data=df).fit()
print results.summary()
year gdp_growth net_approval two_terms incumbent_vote
0 2012 1.3 -0.8 0 52.0
1 2008 1.3 -37.0 1 46.3
2 2004 2.6 -0.5 0 51.2
3 2000 8.0 19.5 1 50.3
4 1996 7.1 15.5 0 54.7
OLS Regression Results
==============================================================================
Dep. Variable: incumbent_vote R-squared: 0.901
Model: OLS Adj. R-squared: 0.878
Method: Least Squares F-statistic: 39.52
Date: Fri, 11 Sep 2015 Prob (F-statistic): 8.50e-07
Time: 21:57:48 Log-Likelihood: -32.747
No. Observations: 17 AIC: 73.49
Df Residuals: 13 BIC: 76.83
Df Model: 3
Covariance Type: nonrobust
================================================================================
coef std err t P>|t| [95.0% Conf. Int.]
--------------------------------------------------------------------------------
Intercept 51.4363 0.811 63.409 0.000 49.684 53.189
gdp_growth 0.5799 0.118 4.903 0.000 0.324 0.835
net_approval 0.0987 0.021 4.764 0.000 0.054 0.143
two_terms -4.2983 1.032 -4.164 0.001 -6.528 -2.069
==============================================================================
Omnibus: 0.333 Durbin-Watson: 1.545
Prob(Omnibus): 0.847 Jarque-Bera (JB): 0.484
Skew: -0.169 Prob(JB): 0.785
Kurtosis: 2.246 Cond. No. 71.4
==============================================================================
İnanılmaz bir başarı, Prob (F-statistic) değeri neredeyse sıfır,
Adj. R-squared değeri yüzde 80'den daha fazla, tüm değişkenler
istatistiki olarak önemli (P>|t| değerleri 0.05'ten küçük).
Acaba bu modeli kullanarak geçmişteki yarışları "tahmin etsek" sonuç ne olurdu diye merak ediyoruz, bunun için tahmin edeceğimiz senenin veri noktasını dışarıda bırakarak (out-of-sample) regresyon işletip o seneyi bilmiyormuş gibi yapıp tahmin ediyoruz,
def out_of_sample_pred(year):
df2 = df[df['year'] != year]
results2 = smf.ols(regr, data=df2).fit()
conf = results2.conf_int()
pred = np.array(df[df['year'] == year])[0][:-1]; pred[0] = 1.
return np.dot(pred, conf)
# o senenin verisinin disarida birakarak gecmisi tahmin et
print 'bush/clinton'; print out_of_sample_pred(1992)
print 'gore/bush'; print out_of_sample_pred(2000)
print 'bush/kerry'; print out_of_sample_pred(2004)
print 'mccain/obama'; print out_of_sample_pred(2008)
print 'obama/romney'; print out_of_sample_pred(2012)
bush/clinton
[ 43.68758927 52.47911415]
gore/bush
[ 48.31291287 60.68132985]
bush/kerry
[ 50.66667848 55.79188333]
mccain/obama
[ 41.05409775 46.15966954]
obama/romney
[ 49.81182614 54.45584122]
Tahmin hesabında değişken katsayılarının \%95 güven aralıklarını veren
conf_int() çağrısını kullandık, değişkenlerin noktasal değerlerini
kullanmadık, bu şekilde tahmine olan güvenimizi aralığın büyüklüğüne bakarak
görebilmiş olacağız. Dikkat: aslında tahminin güven aralığını hesaplamak
biraz daha ek iş gerektiriyor, türetilmesi [12] bölümünde.
Şimdi sonuçlara bakalım; Bush / Kerry yarışı için kesin Bush diyor (çünkü güven aralığının iki ucu da yüzde 50 üstünde), Bush kazandı. McCain / Obama için McCain kesin kaybedecek diyor, McCain kaybetti. Obama / Romney yarışı için Obama (neredeyse) kesin kazanacak diyor, Obama kazandı. Tahminler iyi!
Gore / Bush ilginç bir durum, Gore çok, çok daha şanslı, ama Gore kaybetti. Fakat bu seçimin ne kadar yakın olduğunu o zaman yarısı takip edenler hatırlar, ayrıca, Florida'da bir takım "şaibeli" işlerin (!) olduğu biliniyor, ve model ülke genelinde oyu tahmin etmeye uğraşıyor, ki ülke genelinde bakılınca Gore daha fazla oy almıştı. Amerikan sistemine göre başkanlık seçimleri de eyalet bazında hesaplanır, bir eyalette kazanan tüm oyları alır, bu sebeple ülke geneli ile eyalet bazı arasında uyumsuzluk ortaya çıkabiliyor.
Gore / Bush olayına bir diğer bakış açısı şöyle: oy yüzdesi tahminini yüzdenin kendisi için değil, kazanma / kazanmama için bir sinyal olarak kabul etmek, yani popüler oyun kime gittiğine bakmamak, o zaman modelimizin Göre / Bush seçimini başarısız tahmin ettiğini kabul etmek lazım. Bu şaşırtıcı değil aslında çünkü 2000'de Bush kazandığına kendisi bile şaşırmıştı.
2016 senesindeki yarışta kim kazanacak? Demokratların şansı şöyle (dikkat belli bir adaydan bahsetmiyoruz bile); Haziran 2016 itibariyle büyüme 2\%, Obama'nın net popülaritesi sıfır olduğu durumda (bu değişkenlerin ne olduğuna o tarihte tekrar bakılmalı),
conf = results.conf_int()
pred = [1., 2.0, 0.0, 1]
print np.dot(pred, conf), np.dot(pred, results.params)
[ 43.80446415 52.79105137] 48.2977577583
Yani Demokrat adayın kaybetme şansı daha fazla, her ne kadar kesin bir şey söylenemezse de, güven aralığının iki ucu da yüzde 50 altında (ya da üstünde) değil, Hillary Clinton'un işi zor olacaktı, ki kaybetti. Trump ülke genelinde oy çoğunluğunu kaybetti, ama eyalet bazında kazandı. Demek ki model tahminini kazanma sinyali olarak almak daha uygun.
Analiz
Model oldukça basit, 3 değişken ile tahmin yapılıyor, fakat bu basitlik aldatıcı olabilir. Modele neyin dahil edildiği yanında neyin dahil edilmediği de önemlidir, mesela.. ham petrol fiyatı, işsizlik, seçim yılındaki suç oranı, iklim vs kullanılmamış, sadece bu 3 değişken kullanılmış. Ya da model, Cumhuriyetçiler için ayrı, Demokratlar için ayrı bir tahmin üretmiyor, {\em o an başta hangi parti varsa} onun başarısını tahmin etmeye uğraşıyor. Yani bir bakıma iddiası şu, insanlar aslında başta olan partiye göre oy verirler, bir süre sonra (2 dönem ardından) onu değiştirmeye meyilli olurlar, ve o anda başta olan başkanın popülaritesi ve genel bir ekonomik performansını kullanarak onun partisi hakkında bir tamam / devam kararını verirler. Bu tür modelcilik yetenek ister. Basitlik zor iş!
Tahmin edilirliğin yüksekliği ve değişkenlerin azlığı hakkında bir diğer yorum; bu durum aslında o kadar da şaşırtıcı olmamalı belki de, çünkü başkanlık seçimi son derece kaba hatlı bir karar, tek bir kişi / parti hakkında karar veriliyor, ve doğal olarak seçim için kullanılan parametreler de oldukça genel. Bir bakıma, bu tahmin edilirlik iyi olarak ta görülebilir, stabilite, sakin ortamın işareti olarak algılanabilir. "Vay o taraf ne dedi, bu taraf ne dedi" gibi faktörlerle oylar haldır huldur inip çıkmıyor, belli genel parametreler ışığında sonuç ta dört ay önceden oldukça belli (baz veri Haziran sonu itibariyle alınır, seçim Kasım ayında).
Model Karşılaştırmak
Bu alanda, mesela gazetelerde, yorumlara rastlanıyor. Bunlardan biri "mevcut başkanın (incumbent) ikinci dönem için yarışa girerse avantajlı olduğu" söylemidir, ki üstteki modelin ilk halini keşfeden Abromitz de bunu söylemektedir. Bizim referans aldığımız model [6] o söylemi biraz değiştirmiş, avantajlı olan yerindeki başkan değil, dezavantajlı olan 2 dönemden fazla başta kalan parti. İnsanlar 2 veya daha dönemden fazla başta olan partiyi görevden almaya meyilli oluyor. Tabii eğer parti yeni başa gelmişse, o zaman dezavantaj olmadığı için bazı durumlarda "ilk dönem başkan avantajlıymış gibi" durmuş olabilir. Şimdi bu faraziyeyi test edelim, hangi model daha doğru? Yeni bir veri setinde bu değişikliği test edebiliriz,
import statsmodels.formula.api as smf
import pandas as pd
df = pd.read_csv('prez_incumb.csv')
regr = 'incumbent_vote ~ gdp_growth + net_approval + incumb_prez'
results = smf.ols(regr, data=df).fit()
print results.aic
84.6742088339
AIC sonucu arttı, bu modelin daha kötüleştiği anlamına gelir.
Not: Gayri-safi yurtiçi hasıla (GDP) 2. çeyrekteki artışına bakılıyor. Bu artış bir sene önceye kıyasla değil (year-over-year) bir önceki çeyreğe göre artıştır dikkat, ve sonra bu artış, yıl ölçeğine çıkartılır, $d$ artışı diyelim $(1+\d)^4 - 1$ formülü üzerinden. Yani "her çeyrekte artış $d$ olsaydı, tüm sene artışı nereye gelirdi?" sorusunun cevabı.
Kaynaklar
[1] Teetor, R Cookbook
[2] The Yhat Blog ,Fitting \& Interpreting Linear Models in R, http://blog.yhathq.com/posts/r-lm-summary.html
[3] Abramowitz, {\em Fasten Your Seat Belts: Polarization, Weak Economy Forecast Very Close Election}, http://www.centerforpolitics.org/crystalball/articles/abramowitzpolarizationmodel/
[4] Gelman, A., Bayesian Data Analysis
[5] Bayramlı, Books Data, https://github.com/burakbayramli/books/tree/master/Gelman_BDA_ARM/bda/election
[6] Linzer, R Code, https://github.com/dlinzer/BayesBARUG/blob/master/Linzer-BayesBARUG.R
[7] Bayramlı, Çok Değişkenli Calculus, Ders 9
[8] Bayramlı, Lineer Cebir, Ders 15
[9] Bayramlı, Bilgisayar Bilim, Yapay Zeka, Regresyon, En Az Kareler
[10] Bayramlı, Istatistik, Tahmin Aralıkları
[11] Bayramlı, Istatistik, Güven Aralıkları, Hipotez Testleri
[12] Bayramlı, Istatistik, Tahmin Aralıkları (Prediction Interval)
Yukarı