Bayes Usulü İstatistiki Analiz

Veri analizinde Bayes teorisi kullanımı sayesinde veri olasılığı, bilmediğimiz parametreler hakkındaki bazı bilgilerimizi formülasyona dahil edebiliyoruz. Bunun bir örneğini MAP hesaplarını [4] işlerken gördük. Bu bölümde Bayes formüllerinin sonuçlarını bulmak için bazı hesapsal teknikleri işleyeceğiz, ve niye faydalı olduklarını anlamaya uğraşacağız. Temel olasılık teorisinden biliyoruz ki Bayes teorisi

diye gider. Üstteki formülü veri analizine uyarlayabiliriz. İstatistiki modelin parametreleri \(\theta\)’yi \(A = \theta\) yaparız, \(B = \textrm{veri}\) diyelim, o zaman Bayes teorisi eldeki verinin parametre hesabı \(\theta\) için nasıl kullanılacağının formülünü gösterir [3, Chapter 1],

\[ P(\theta | \textrm{veri}) = \frac{P(\textrm{veri} | \theta) \times P(\theta)}{P(\textrm{veri})} \]

Formül öğelerinin açıklamasını [4] yazısında bulabiliriz. Tekrarlamak gerekirse, sol tarafta, veriyi gördükten sonra ne bildiğinizi temsil eden, sonsal dağılım olan \(P(\theta \mid \text{veri})\) bulunur. Bu, çıkarımın temelini oluşturur ve açıkça aradığınız şeydir; eğer birden fazla parametreniz varsa, muhtemelen çok değişkenli bir dağılım. Sağ tarafta, olurluk olan \(P(\text{veri} \mid \theta)\) bulunur. Bu miktar, En Yüksek Olurluk Tahmini (MLE) yaklaşımındaki ile aynıdır. Evet, Bayesçi ve frekansçı yaklaşımların çekirdeğinde aynı olurluk bulunur, bu da sonuçların genellikle neden çok farklı olmadığını büyük ölçüde açıklar. Olurluk, \(\theta\) ile parametrelendirilmiş bir model verildiğinde, verinizdeki bilginin olasılığını gösterir. Dikkat, \(P(\textrm{veri})\) ve \(P(\theta)\) tanımları ile bu iki öğeyi birer rasgele değişken olarak formülasyona dahil etmiş oluyoruz. Bunun ne anlama geldiğini [4]’te işledik.

Ardından, önsel dağılım olan \(P(\theta)\) gelir. Bu miktar, veriyi görmeden önce ne bildiğinizi temsil eder. Eğer \(\theta\) hakkında hiçbir şey bilmiyorsanız, belirsiz olabilir. Ancak genellikle sıfırdan başlamazsınız ve önselinizin sahip olduğunuz bilgiyi yansıtmasını istersiniz, mesela bir zar atımında zarların 1 ve 3 arası gelmesi daha muhtemel ise bu bilgiyi bir önsel olasılık olarak modele dahil etmek mümkündür.

Son olarak, bazen “ortalama olurluk” olarak adlandırılan \(P(\text{veri})\) bulunur, çünkü sonsalın standartlaştırılması, yani bir dağılım olması için bire entegre olması amacıyla, olurluk önsele göre entegre edilerek elde edilir: \(P(\text{veri}) = \int P(\text{veri} \mid \theta) P(\theta)d\theta\). Ortalama olurluk, tahmin etmeniz gereken \(\theta\) parametrelerinin sayısı boyutunda bir integraldir. Bu, genel olarak hesaplanması imkansız olmasa da zordur. Bayesçi yöntemin yakın zamana kadar kullanılmamasının nedenlerinden biri de budur.

Örneğin, ekolojide kullanilan bir yakalama-tekrar yakalama modelini, tespit olasılığı \(p\) ve hayatta kalma olasılığı ile bir kovaryat arasındaki ilişkinin kesişim ve eğimi için regresyon parametreleri \(\alpha\) ve \(\beta\) ile uyarlamak istediğinizi düşünün. Bu durumda Bayes teoremi, her üç parametrenin birlikteki sonsal dağılımını size verir:

\[P(\alpha, \beta, p \mid \text{veri}) = \frac{P(\text{veri} \mid \alpha, \beta, p) \times P(\alpha, \beta, p)}{\iiint P(\text{veri} \mid \alpha, \beta, p) P(\alpha, \beta, p)d\alpha d\beta dp}\]

Bu formülde bir hesaplama zorluğu var. Bölende üç boyutlu bir integrali görüyoruz, bu entegral çok çetrefilli bir çözümdür, analitik çözüm çoğunlukla mümkün değildir, hesapsal yaklaşımlar gerekir. Bu entegralin her durumda hesaplanması gerekmeyebiliyor, mesela [4]’te gördük ki aranılan bir parametre maksimize edilmeye çalışılan büyüklükte bölen değerine ihtiyaç duymuyordu, bu sebeple onu yok sayabildik. Fakat bazen bölendeki entegral kesinlikle gerekir, mesela iki farklı Bayes modelini karşılaştırıyorsak, bölendeki değer iptal edilemez, ve hesaplanması gerekir.

Fakat bölümdeki entegral lazım olmasa bile, yani normalize edici katsayıyı bilmeden yine de sonsal dağılıma “orantılı” bir sonuç elde edebilsek bile, orada da analitik sonuç alamayacağımız ortaya çıkabiliyor, ve orada için yine yaklaşık yöntemlere başvurmamız gerekiyor.

Bir deneyde tepki süresi ölçümlerinden oluşan tek değişkenli verilere sahip olduğumuzu varsayalım. Bu veriyi modellemek için, Weibull dağılımının faydalı bir tanımlayıcı model olacağını varsayalım [6, sf. 42].

Bu dağılımın iki parametresi vardır: a dağılımın ölçeğini ve b ise dağılımın şeklini kontrol eder. Verilerimizin \(y_{i}\) ile temsil edildiğini, \(i\in1..N\) olduğunu ve \(N\)’nin gözlem sayısını gösterdiğini varsayalım. Modelimizde, her gözlemin bir Weibull dağılımından bağımsız bir çekiliş olduğunu varsayalım.

Bu varsayımlar göz önüne alındığında, verilerimiz için artık bir olurluk fonksiyonuna (likelihood function) sahibiz. Her gözlemin \(a\) ve \(b\) parametrelerine sahip bir Weibull’dan bağımsız bir çekiliş olduğu varsayılırsa, tüm gözlemlerin olasılığı şu şekilde verilir:

\[p(y_{1},...,y_{N}|a,b)=p(y_{1}|a,b)p(y_{2}|a,b)...p(y_{N}|a,b)\] \[=\prod_{i}p(y_{i}|a,b)\] \[=\prod_{i}ba^{-b}y_{i}^{b-1}e^{-{(\frac{y_{i}}{a})}^{b}}I_{(0,inf)}(y_{i})\]

Ancak model tanımımızla henüz tamamen işimiz bitmedi. Her Bayesci analizde, parametreler üzerinde önsel dağılımları (prior distributions) da belirtmemiz gerekir. \(a\) ve \(b\) parametrelerinin sırasıyla \(\lambda_{a}\) ve \(\lambda_{b}\) parametrelerine sahip bir üstel dağılıma (exponential distribution) göre bağımsız olarak dağıldığını varsayalım.

\[p(a|\lambda_{a})=\frac{1}{\lambda_{a}}e^{-\frac{a}{\lambda_{a}}}\] \[p(a|\lambda_{b})=\frac{1}{\lambda_{b}}e^{-\frac{b}{\lambda_{b}}}\]

Yukarıda ifade edilen modelin, örnekleme notasyonu (sampling notation) kullanılarak çok daha basit terimlerle açıklanabileceğini belirtmeliyiz:

\[\begin{array}{l}y_{i}|a,b\sim Weibull(a,b)\\a\sim Exp(\lambda_{a})\\b\sim Exp(\lambda_{b})\end{array}\]

Artık hem bir olurluk hem de tüm parametreler üzerinde bir önsel içeren, tamamen belirlenmiş bir modele sahibiz. Amaç, sonsal çıkarım (posterior inference) yapmak ve verilere koşullu olarak parametreler üzerindeki sonsal dağılımı bulmaktır.

Bizim durumumuzda, \(\theta=(a,b)\) ve \(D=(y_{1},...,y_{N})\)’dir. Bu nedenle, şunu yazabiliriz:

\(a\) ve \(b\) parametreleri üzerinde bağımsız önsel kullanmaya karar verdiğimize dikkat edin. Bu bize şunu yazma olanağı verir:

Bu sonsal dağılımın fonksiyonel biçiminin neye benzediğini görmek için açılımı yapalım,

\[p(a,b|y_{1},...,y_{N}) \propto \left( \prod_{i}ba^{-b}y_{i}^{b-1}e^{-(\frac{y_{i}}{a})^{b}}I_{(0,inf)}(y_{i}) \right) \frac{1}{\lambda_{a}}e^{-\frac{a}{\lambda_{a}}} \frac{1}{\lambda_{b}}e^{-\frac{b}{\lambda_{b}}} \]

Hangi durumlarda çetrefil entegral hesapları muhakkak şart oluyor? Mesela farklı modellerin olurluk oranı (likelihood ratio) karşılaştırılması gerektiğinde ekstra hesap şart. “Ama hem bölen hem bölünende aynı büyüklük / normalize edici sabit var ise birbirlerini iptal etmezler mi?”. Ne yazik ki farklı Bayes modellerinin farklı sabit edicileri olur, bu durumda iptal mümkün olmaz. Yani \(M1\) ve \(M2\) modelleri var ise, bir entegral \(\int P_{a}(\text{veri} \mid \theta) P_b(\theta)d\theta\) digeri \(\int P_{c}(\text{veri} \mid \theta) P_d(\theta)d\theta\) olabilir, bu hesaplar farklı sonuçlar verecektir çünkü farklı yoğunluk fonksiyonları ve parametreleri kullanıyor olurlar.

PyMC

Programcıları üstte tarif edilen hesapsal yükten kurtarmaya uğraşan ve hesapların daha rahat programlanmasını sağlayan paketler var. Bu paketler önsel / sonsal rasgele değişkenlerin kodlanmasını neredeyse tanımsal (declarative) hale getirerek alt seviye kodlama detaylarını perde arkasına itebiliyorlar, ve bu şekilde Bayesçi hesapların çabuk gerçekleştirilmesini sağlıyorlar. Bu paketler sayesinde istenildiği kadar rasgele değişken bağlantısı yaratalım, çözücü kodlar sonsal dağılımdan örneklem alabiliyor. Bu tür paketler getirdikleri rahatlık sayesinde neredeyse bir dil yaratmış oluyorlar, ve bazıları terminolojiye yeni bir terim ekliyor: olasılıksal programlama (probabilistic programming).

Bir örnek üzerinde görelim [7, sf. 8]. Standart istatistik örneklerinden bilindiği gibi art arda atılan madeni paranın yazı mı tura mı geleceği (daha doğrusu \(N\) deney içinde \(k\) başarı olasılığı) Binom dağılımı ile temsil edilebilir. Dağılım \(X \sim Bin(N,p)\) ile gösterilebilir, ki \(X\) rasgele değişken yoğunluğu

Eğer yanlılık yok ise \(p=0.5\), var ise mesela \(p = 0.7\). Eğer yoğunluğu verilen ve bilinen \(p\) yoğunluğundan rasgele örneklem toplamak istesek bunu yapabilirdik, yaygın kullanılan kütüphanelerde bile böyle kodlar mevcuttur. Eğer \(p\) bilinmiyor olsaydı ve elde deney verisi olsaydı, bilinmeyen \(p\)’yi bu veriden kestirmenin de yöntemleri mevcuttur.

Modeli daha çetrefilleştirebilirdik. \(p\)’nin bilinip bilinmedigi bir yana, onu tek bir sayı ile değil, bir rasgele değişken, mesela \(\theta\) üzerinden tanımlıyor olabilirdik. O zaman \(\theta\)’nın da ayrı bir dağılımı olurdu.

Şimdi rasgele örneklem üretmek iki aşamalı oldu, önce bir Beta dağılımından örneklem alınacak, sonra bu alınan değer Bin dağılımından örneklem için kullanılacak.

PyMC kodları burada devreye giriyor, Bayes yaklaşımı ile iki katmanlı bir yapı oluşturduk, bir rasgele değişken diğerine bağlı, ve biz mevcut veriyi de hesaba katan bir sonral dağılım \(\theta\)’dan örneklem alabiliriz.

import pymc as pm, scipy.stats as stats
import pandas as pd

Y = stats.bernoulli(0.7).rvs(20)

with pm.Model() as model:
     theta = pm.Beta("theta", alpha=1, beta=1)
     y_obs = pm.Binomial("eta_obs", n=1, p=theta, observed=Y)
     idata = pm.sample(1000, return_inferencedata=True)

theta_post = np.array(idata.posterior['theta'])
print (np.mean(theta_post))
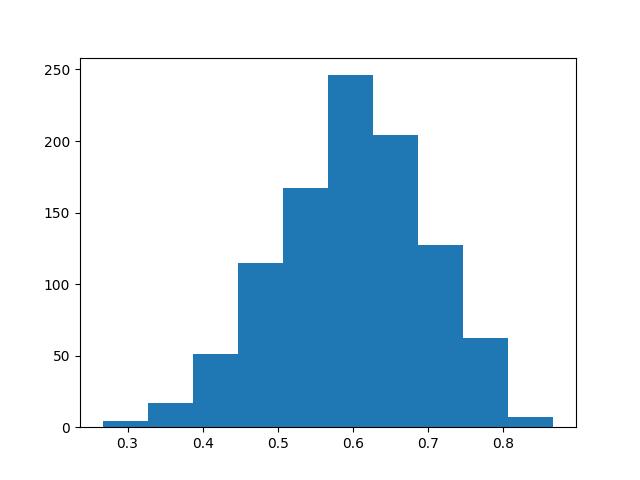
plt.hist(theta_post[0],bins=10)
plt.savefig('tser_023_bsts_03.jpg')

Görüldüğü gibi 0.7 odaklı yanlı veriyi modele verince kodlar bunun sonsal \(\theta\) dağılımına yansımasını saptadı, ortalama 0.72 çıktı. Ayrıca tek bir sayı değil, bütün bir dağılımı sonuç olarak aldığımız için çok daha çetrefil analizleri bu sonuçtan alabiliriz.

graphviz = pm.model_to_graphviz(model)
graphviz.graph_attr.update(dpi="300")
graphviz.render("tser_023_bsts_02", format="jpg")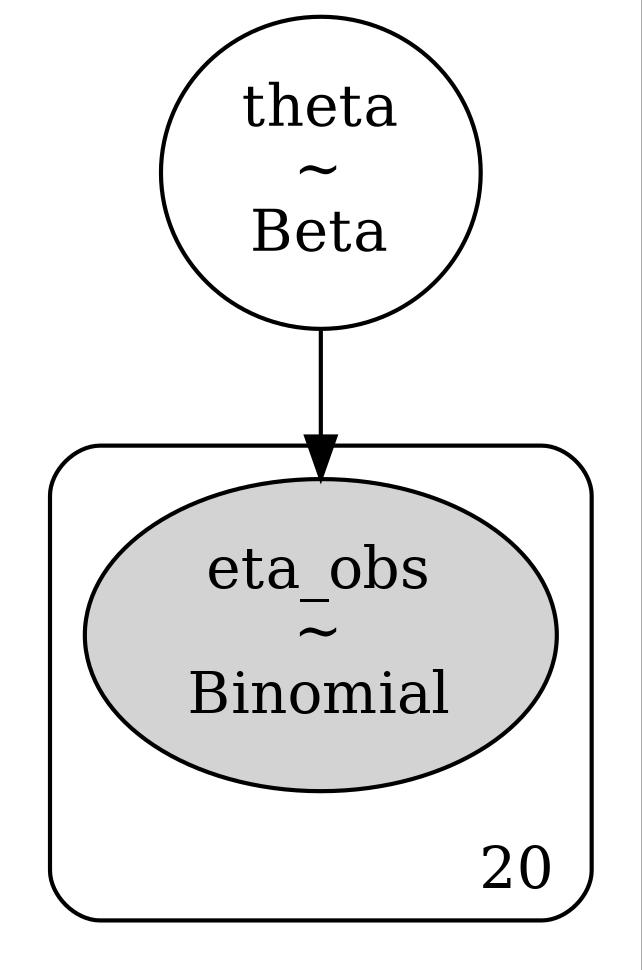

T-Testi

Bayesçi yaklaşımın farkını üstteki örnekte görmeye başladık. Parametreler hatta veri bile bir rasgele değişken haline gelebiliyordu. Bu yaklaşım istatistiki analizin tüm alanlarında fark yaratabilir, mesela hipotez testi kavramına da Bayesci sekilde yaklasabiliriz. Standart müfredatta iyi bilinen t-testini örnek alalım, bu test örneklem ortalamasının önceden tanımlı bir değerden sapma durumunu kontrol eder. T-testinin Bayes versiyonu Kruscke tarafından bulunmuştur, BEST (Bayesian Estimation Supersedes the t-test) yontemi [1].

Diyelim ki iki grubu birbiriyle karşılaştırıyoruz, pazarlamacıların iyi bildiği bir A/B testi gerçekleştirmemiz gerekiyor. Test edilen iki Web sayfası olabilir, ve kullanıcıların her sayfada ne kadar kaldığı verisi iki ayrı grupta kaydedilmiş olsun. Merak ettiğimiz kullanıcıların hangi sayfada daha fazla kaldığı, A sayfasında mı, B sayfasında mı?

N = 250
mu_A, std_A = 30, 4
mu_B, std_B = 26, 7

durations_A = np.random.normal(mu_A, std_A, size=N)
durations_B = np.random.normal(mu_B, std_B, size=N)

print (durations_A[:8])
print (durations_B[:8])

İki farklı grubun farklı ortalaması, ve standart sapması var, veriyi ona göre ürettik. Doğal olarak bir sayfadaki (A) kullanıcı zamanı diğerinden (B) daha fazla. Şimdi acaba birazdan göreceğimiz t-testi bu farkı yakalayabilecek mi?

Verileri np.r_ ile birleştirip bu birleşik verinin ortalama ve standart sapmasını hesaplıyoruz.

pooled_mean = np.r_[durations_A, durations_B].mean()
pooled_std = np.r_[durations_A, durations_B].std()

Bunu yapmamızın sebebi analize verilecek başlangıç değeri olarak kabaca bir değeri saptamak. Şimdi modelin geri kalanını ortaya çıkartalım. Bayes veri analizi değişken bağlantılarını düşünürken iyi bir yöntem şudur, “acaba bu veriyi nasıl üretirdim” diye düşünmek. Mesela \(\theta\) ile tanımlı madeni para atışlarında adımlar şöyledir, “önce rasgele \(\theta\) üret, sonra bu \(\theta\) ile Binom üretimi yap”.

O zaman ziyaret zamanlarını iki ayrı Student-T dağılımından “ürettiğimizi” düşünelim. Bu dağılımlara gereken parametreler \(\mu,\sigma,\nu\) iki dağılım için \(\mu_A,\sigma_A,\mu_A\),.. diye giderler. Bayesçi yaklaşımda bu değişkenlerin de dağılımları var, \(\mu_A,\mu_B\) Gaussian dağılımı olsun (başlangıç değerleri pooled_mean), \(\sigma_A,\sigma_B\) birörnek dağılımdan gelsin, ve pooled_std’yi temel alsın, ve oldukça geniş bir değer yelpazesini tanımlasın, fazla kısıtlama yapmaya gerek yok.

\(\nu_A,\nu_B\) için dikkat edilirse farklı bir önsel (prior) dağılım tanımladık, üstel (exponential) dağılım. Bunun sebebi \(\nu\) parametresinin Student-T üzerinde logaritmik skalada bir etki yaratmasıdır, kabaca \(\nu = 1-10\) değerleri Student-T dağılımında “kabarık eteklere” tekabül eder, \(\nu = 10-30\) arasında etekler ortalama olur, \(\nu > 30\) ile dağılım Gaussian’a benzemeye başlar. Görüldüğü gibi bu aralıklar eşit bölünmüş değildir, bir logaritmik durum var. Bu sebeple eğer Student-T için birörnek’imsi bir önsel tanım yapmak istiyorsak bunu üstel dağılım üzerinden yapmamız gerekir. \(\lambda = 1/29\) ile \(\nu-1 = 29\) olur, ya da \(\nu = 30\). Böylece Gaussian’a benzeyen Student-T (\(\nu \ge 30\)) ile etekleri daha kabarık bir Gaussian’imsi dağılım (\(\nu < 30\)) arasında bir denge kurmuş oluyoruz.

Ve nihai analiz için gerekecek son tanım: analiz bize \(\mu_A\) ve \(\mu_B\) sonsal dağılımlarını verecek. Peki bu dağılımlardan hangisi “daha büyük”. Bu hesabın kolay yolu var, bir dağılımı diğerinden çıkartırız. Ama bu çıkartma işlemini de PyMC üzerinden yapmamız gerekiyor, bir Deterministic değişken içinde iki dağılımın farkını \(\mu_A - \mu_B\) hesaplatırız, böylece bu çıkartma işlemi simülasyonun parçası haline gelir, ve sonuç, ki o da bir rasgele değişkendir, en sonda alınıp grafiklenebilir. Eğer bu grafikteki dağılımın çoğu, hatta tamamı sıfır değerinin sağında oluyor ise (hep pozitif değerler) o zaman A dağılımından gelen değerler B sayfasındaki değerlerden büyüktür, yani A sayfasında daha fazla zaman geçirilmiştir.

# Build the model in modern PyMC
with pm.Model() as model:
    # Priors
    mu_A = pm.Normal("mu_A", mu=pooled_mean, sigma=1000*pooled_std)
    mu_B = pm.Normal("mu_B", mu=pooled_mean, sigma=1000*pooled_std)
    
    std_A = pm.Uniform("std_A", lower=pooled_std/1000., upper=1000.*pooled_std)
    std_B = pm.Uniform("std_B", lower=pooled_std/1000., upper=1000.*pooled_std)
    
    nu_minus_1 = pm.Exponential("nu_minus_1", lam=1./29)
    nu = pm.Deterministic("nu", nu_minus_1 + 1)
    
    # Likelihood - using StudentT instead of NoncentralT
    obs_A = pm.StudentT("obs_A", nu=nu, mu=mu_A, sigma=std_A, observed=durations_A)
    obs_B = pm.StudentT("obs_B", nu=nu, mu=mu_B, sigma=std_B, observed=durations_B)
    
    # Derived quantities (deterministic nodes)
    diff_of_means = pm.Deterministic("diff_of_means", mu_A - mu_B)
    diff_of_stds = pm.Deterministic("diff_of_stds", std_A - std_B)
    effect_size = pm.Deterministic("effect_size", 
                                    (mu_A - mu_B) / pm.math.sqrt((std_A**2 + std_B**2) / 2))
    
    # Sample
    trace = pm.sample(2000, tune=1000, return_inferencedata=False, cores=1)

graphviz = pm.model_to_graphviz(model)
graphviz.graph_attr.update(dpi="300")
graphviz.render("stat_047_bayes_02", format="jpg")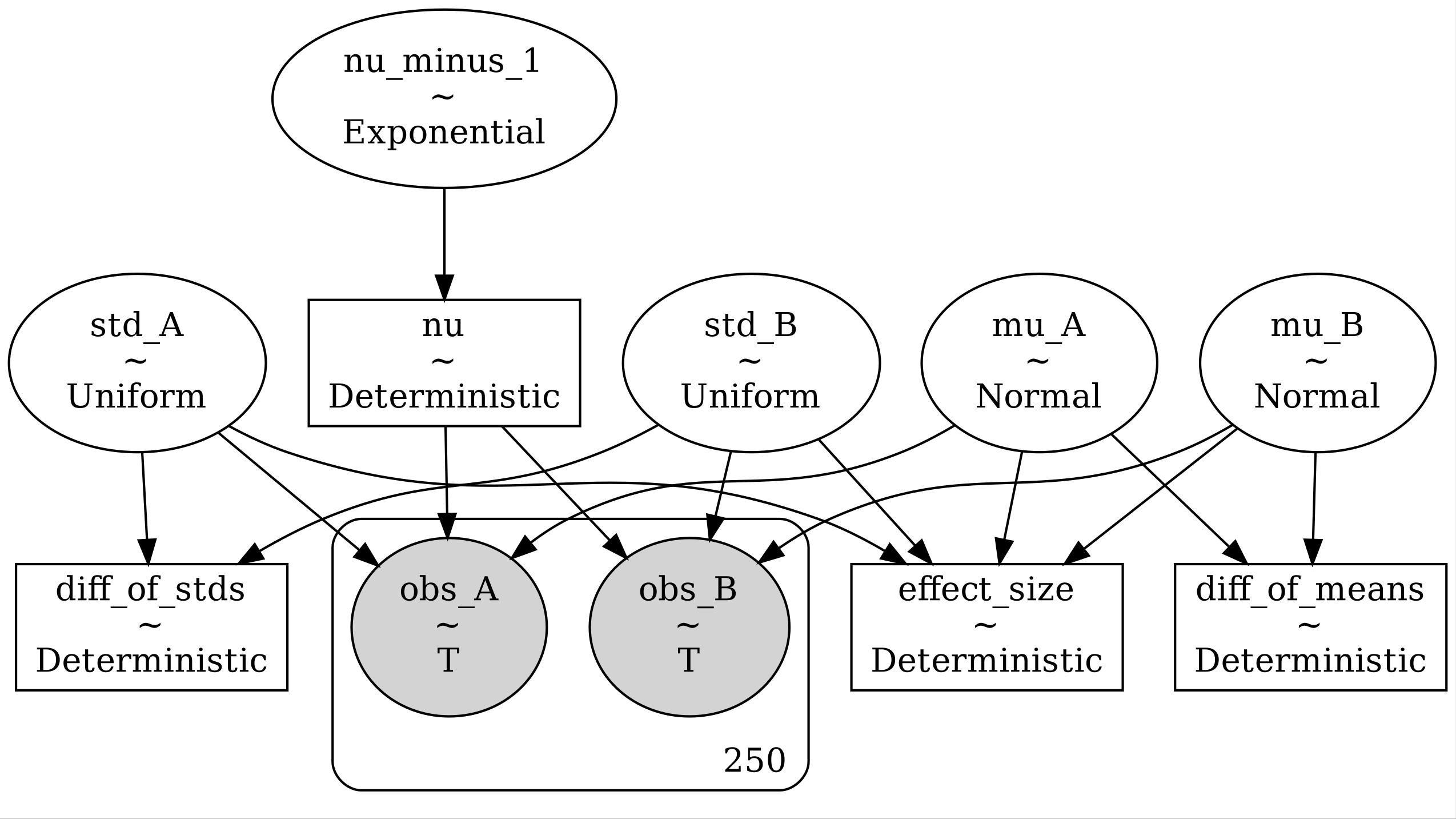

diff_means_trace = trace['diff_of_means']
diff_stds_trace = trace['diff_of_stds']
effect_size_trace = trace['effect_size']

plt.figure(figsize=(10, 4))
plt.hist(diff_means_trace, bins=50, histtype='stepfilled', alpha=0.85, density=True)
plt.axvline(0, color='red', linestyle='--', label='Sifir (Null) Hipotezi')
plt.xlabel('μ_A - μ_B')
plt.ylabel('Yogunluk (Density)')
plt.title('Ortalama Farki Sonsal Dagilimi')

# Sifirdan buyuk olma yuzdesi
pct_greater = (diff_means_trace > 0).sum() / len(diff_means_trace) * 100
pct_less = (diff_means_trace < 0).sum() / len(diff_means_trace) * 100
plt.text(0.7, 0.9, f'{pct_less:.1f}% < 0 < {pct_greater:.1f}%', 
         transform=plt.gca().transAxes, fontsize=12)

plt.legend()
plt.tight_layout()
plt.savefig('stat_047_bayes_01.jpg')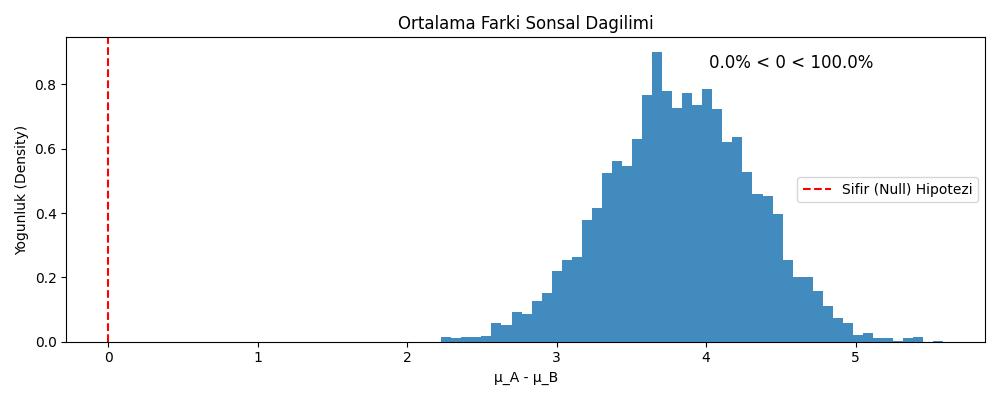

Sonuç gösteriyor ki dağılımdaki değerler sıfırın sağında, yani kullanıcılar A sayfasında daha fazla zaman geçirmiş. Zaten suni yarattığımız rasgele veride bunun böyle olduğunu biliyorduk, analiz ile doğrulanması iyi oldu.