Binom İçin Normal Yaklaşıksallığı
Merkezi Limit Teorisinden $\bar{X}$'nin her $X_i$ için aynı olan nüfus beklentisi ve sapmasını içeren $N(\mu,\sigma)$ olarak dağılacağını biliyoruz. Ve bu durum, nüfus hangi dağılıma sahip olursa olsun geçerlidir. $X_1,..,X_n$ birbirinden bağımsız ve aynı Bernoulli olarak dağılmış, ve onların toplamını temsil eden binom dağılımı $X$ olarak tanımlayalım, o zaman
$$ X = X_1 + X_2 + .. + X_n $$
Daha önceden biliyoruz ki $E(X_i) = p, Var(X_i) = p(1-p)$, standart sapma varyansın karekökü. O zaman Merkezi Limit Teorisine göre,
$$ Z = \frac{X/n - p}{\sqrt{p(1-p)/n}} = \frac{X - np}{\sqrt{np(1-p)}} $$
Soru
Amerikalıların yüzde 12'sinin zenci olduğunu biliyoruz. Eğer 1500 kişiyi içeren bir örneklem alsaydık, bu örneklemde 170'den daha az zenci olmasının olasılığı nedir?
Cevap
\%12 nüfus parametresidir, yani $p=0.12$. Örneklem $n=1500$. Normal yaklaşıksallaması ile
from scipy.stats import norm
n = 1500
p = 0.12
mu = n*p
std = np.sqrt(n*p*(1-p))
print mu,std
print 'olasilik',norm.cdf(170,loc=mu,scale=std)
180.0 12.585706178
olasilik 0.213437028747
Yani $N(180,12.58)$ dağılımını elde ettik ve hesapları onun üzerinden yaptık. Sonuç diyor ki verilen örneklem ve nüfus $p$ değeri ile 170 altında zenci sayısı elde etmek oldukça düşük bir ihtimalde.
Örnek
Diyelim ki elimizde bir Web sitesinin günlük ziyaret, tıklama sayılarını gösteren bir veri seti var, CVR ziyaretçilerin sitedeki tıklayan müşteriye dönüşmesi oranı (conversion).
import pandas as pd
from scipy import stats
a = pd.DataFrame({'tiklama': [20.,2.,40.,5.,10.,100.],
'ziyaret': [100.,10.,300.,400.,30.,800.]})
a['cvr'] = a['tiklama'] / a['ziyaret']
print a
tiklama ziyaret cvr
0 20 100 0.200000
1 2 10 0.200000
2 40 300 0.133333
3 5 400 0.012500
4 10 30 0.333333
5 100 800 0.125000
Bu veri seti için cvr'in 0.16, yani yüzde 16 olduğunu önceden biliyoruz. Üstteki başarı oranı binom dağılı ile modellenebilir, ziyaretler "deneylerdir", yani örneklem büyüklüğünü gösterirler. Tıklama ise başarıdır, önceki binom örneğindeki aynı formülü kullanırsak, normal yaklaşıksallığı üzerinden bir z-skoru hesaplayabiliriz,
p = 0.16
btest = lambda x: (x['cvr']-p) / np.sqrt( p*(1-p)/x['ziyaret'])
a['guven'] = a.apply(btest, axis=1)
a['guven'] = np.round(stats.zprob(a['guven'])*100,2)
print a
tiklama ziyaret cvr guven
0 20 100 0.200000 86.24
1 2 10 0.200000 63.50
2 40 300 0.133333 10.39
3 5 400 0.012500 0.00
4 10 30 0.333333 99.52
5 100 800 0.125000 0.35
Soru
Amerika'da 2009 yılında halkın ne kadarının arabalarında yakıt tasarrufunu desteklediği merak konusuydu. Bir Gallup telefon anketinde bu soru 1012 yetişkine (18 ve üstü yaşta) soruldu. Cevap 810 kişinin tasarrufu desteklediği yönündeydi. Yani $n=1012,k=810$. O zaman $p$ için \%95 güven aralığını bulun.
Cevap
$$ \bigg( \frac{810}{1012} -1.96 \sqrt{ \frac{(810/1012)(1-810/1012)}{1012} } , 1.96 \sqrt{ \frac{(810/1012)(1-810/1012)}{1012} } \bigg) $$
$$ = (0.776,0825) $$
Python ile
m = 810/1012.
low = m - 1.96*np.sqrt(m*(1-m)/1012.)
high = m + 1.96*np.sqrt(m*(1-m)/1012.)
print low, high
0.775768711331 0.825021802503
Soru
Borsa konusunda okuyuculara tiyo veren bir gazete, bir şirket hissesinin belli bir olay ardından çoğunlukla yükseldiğini söylüyor. Yazara göre hisse 9 olay içinden 6'sında bu çıkmış. Buradan hareketle yazar hissenin tekrar çıkma şansının 6/9=\%66.7 olduğunu iddia ediyor. Okuyucu bunu ciddiye alsın mı?
Cevap
Ufak örneklemler için Agresti ve Coull yöntemini kullanmak iyi olur, bu yönteme göre başarılı olay sayısına iki, tüm olay sayısına 4 ekleriz (yani 2 başarısızlık eklemiş oluruz) ve $\hat{p} = (x+2)(n+4)$ elde edilir. Bu ekler hem genel teorik olarak bir değişim yaratmaz, hem de örneklem sayısını arttırarak Normal yaklaşıksallığını kullanabilmemizi sağlar. Güven aralığı,
x=6.;n=9.;p=(x+2)/(n+4); z = 1.96
print p + np.array([-1,+1])*z*np.sqrt(p*(1-p)/n)
[ 0.29753517 0.93323406]
Demek ki yazar okuyucularına kötü bir tavsiye vermiş, güven aralığının alt kısmı \%30 olduğuna göre hissenin yükselmesi garanti değildir, garanti için güven aralığının iki ucu da \%50 üzerinde olmalıydı. Noktasal tahmin bağlamında \%66.7 rakamı da yanıltıcıdir. Bu yazar okuyucularının para kaybetmesine sebep olabilir.
Örneklem Büyüklüğü
Bir araştırmacı $n$ bağımsız deney baz alınarak elde edilen binom parametresi $p$'yi tahmin etmek istiyor, fakat kaç tane $n$ kullanması gerektiğini bilmiyor. Tabii ki daha büyük $n$ değerleri daha iyi sonuçlar verecektir, ama her deneyin bir masrafı vardır. Bu iki gereklilik nasıl birbiri ile uzlaştırılır?
Yeterli olacak en az kesinliği, duyarlılığı (precision) bulmak için Z transformasyonu kullanılabilir belki. Diyelim ki $p$ için maksimum olurluk tahmini olan $X/n$'in en azından $100(1-\alpha)\%$ olasılıkta $p$'nin $d$ kadar yakınında olmasını istiyoruz. O zaman alttaki denklemi tatmin eden en ufak $n$'i bulduğumuz anda problemimizi çözdük demektir,
$$ P\bigg( -d \le \frac{X}{n} - p \le d \bigg) = 1-\alpha \qquad (1) $$
Tahmin edici $X/n$'nin kendisi de bir rasgele değişkendir. Bu değişken normal olarak dağılmıştır, çünkü $X$ Binom olarak dağılmış ise, bu dağılım ayrı Bernoulli dağılımlarının toplamına eşittir. Fakat başka bir irdeleme bizi daha basitçe sonuca götürür, binom dağılımı bir toplamdır, bu toplamı, yani $X$'i $n$ ile bölüyorsak, otomatik olarak bir aritmetik averaj işlemi yapmış oluyoruz. Bağımsız özdeşçe dağılmış (ıid) rasgele değişkenlerin aritmetik ortalaması Merkezi Limit Kanunu'na göre normal'e yaklaştığına göre o zaman, elimizde bir normal dağılım var demektir.
Standardize etmek için $X/n$'den beklentiyi çıkartıp standart sapmaya bölebiliriz. Beklenti zaten çıkartılmış durumda (şansa bak!), beklentinin ne olduğunu kontrol edelim tabii, ezbere yapmayalım bu işi, eğer her Bernoulli'yi $X_i$ olarak temsil edersek,
$$ X = X_1 + .. + X_n $$
$$ X/n = 1/n(X_1 + .. + X_n )$$
$$ E[X/n] = E[1/n(X_1 + .. + X_n )]$$
$$ = 1/nE[(X_1 + .. + X_n )]$$
$$ = (1/n)np = p$$
Varyans için
$$ Var(X/n) = \frac{1}{n^2}Var(X) = \frac{1}{n^2}np(1-p)= \frac{1}{n}p(1-p) $$
Binom dağılımlar için $Var(X) = np(1-p)$ olduğunu biliyoruz. Standart sapma üstteki ifadenin karekökü, yani
$$ Std(X/n) = \sqrt{p(1-p)/n} $$
Simdi standardize edelim,
$$ P\bigg( \frac{-d}{\sqrt{p(1-p)/n}} \le \frac{\frac{X}{n} - p }{\sqrt{p(1-p)/n}}\le \frac{d}{\sqrt{p(1-p)/n}} \bigg) = 1-\alpha$$
$$ P\bigg( \frac{-d}{\sqrt{p(1-p)/n}} \le Z \frac{d}{\sqrt{p(1-p)/n}} \bigg) = 1-\alpha$$
Daha önceki z-skoru içeren eşitsizlikleri hatırlarsak, üstteki ifade
$$ \frac{d}{\sqrt{p(1-p)/n}} = z_{\alpha/2} $$
O zaman
$$ \frac{z_{\alpha/2}^2p(1-p)}{d^2} = n $$
Fakat bu bir nihai sonuç olamaz, çünkü $n$, $p$'nin bir fonksiyonun haline geldi ve $p$ bilinmeyen bir değer. Fakat biliyoruz ki $0 \le p \le 1$, ve $p(1-p) \le \frac{1}{4}$. Yani bir üst sınır (upper bound) elde ettik.
Bunu kontrol edelim, $p(1-p)$ hangi $p$'de maksimize olur? $p$'ye göre türev alırız, sıfıra eşitleriz, $(p-p^2)' = 1 - 2p = 0, p=1/2$. Ve hesabı yaparsak, $1/2(1-1/2)=1/4$. Demek ki $p(1-p)$ değeri $1/4$'ten daha büyük olamaz. Buna göre, üstteki formüle $p(1-p)$ yerine onun olabileceği en büyük değeri koyarsak,
$$ \frac{z_{\alpha/2}^21/4}{d^2} = n $$
$$ n = \frac{z_{\alpha/2}^2}{4d^2} $$
Not: $p(1-p)$, 1/4 değerinden daha küçük olabilir mi? Olabilir. Bu durumda $n$ üstteki formülden elde edebileceğimiz değerden daha küçük te çıkabilecektir. Fakat $p(1-p)$'in olabileceği en büyük değer 1/4'u kullanarak "$n$'in bundan daha büyük olmasına gerek yok" diyebilen bir formüle erişmiş olduk, yani, aslında $n$ için bir üst sınır elde ettik.
Örnek
Büyük bir şehirde çocukların kaçta kaçının aşısını almış olup olmadığını anlamak için bir anket gerçekleştirilecek. Anketi düzenleyenler örneklem oranı olan $X/n$'in en az 98\% oranda gerçek oran $p$'nin 0.05 yakınında olmasını istiyorlar. Örneklem ne kadar büyük olmalıdır?
Burada $100(1-\alpha) = 98$, o zaman $\alpha = 0.02$, demek ki $z_{\alpha/2} = z_{0.02/2} = z_{0.01}$ değerine ihtiyacımız var. Python ile
from scipy.stats.distributions import norm
print norm.ppf(0.99)
2.32634787404
Tüm hesap için
$$ n = \frac{(2.33)^2}{4(0.05)^2} = 543$$
Demek ki kabul edilebilir en ufak değer 543.
Hata Payı (Margin of Error)
Basında oranları rapor ederken onunla beraber telafuz edilen bir kavram hata payıdır. Aslında bu binom dağılımlarda güven aralığı ile çok yakından alakalıdır; hata payı \%95 güven aralığının en maksimum genişliğinin yarısı olarak bilinir. Yani \%95 aralığının bir ucunu diğer ucundan çıkartırsak ve ikiye bölersek, istenen sonuca erişiriz. Formülsel olarak genişlik $w$,
$$ w = \frac{k}{n} + 1.96 \sqrt{\frac{(k/n)(1-k/n)}{n}} - - \bigg[ \frac{k}{n} - 1.96 \sqrt{\frac{(k/n)(1-k/n)}{n}} \bigg] $$
$$ = 3.92 \sqrt{\frac{(k/n)(1-k/n)}{n}} $$
Şimdi $(k/n)(1-k/n)$ çarpımını düşünelim. [8] bölümünde gördük, $n$ her zaman $k$'den büyük olduğuna göre $k/n$ her zaman 0 ve 1 arasındadır, o zaman $(k/n)(1-k/n) \le 1/4$ olmalıdır, yani gösterilen çarpım 1/4'ten büyük olamaz. Bunu alıp üstteki formül içine koyarsak,
$$ \max w = 3.92 \sqrt{\frac{1}{4n}} $$
elde ederiz. Bunun yarısı hata payıdır $d$ olur, yani
$$ d = \frac{0.98}{\sqrt{n}} $$
Örnek
Bir seçim kampanyası sırasında A ve B adayları arasında hangisinin daha önce olduğunu bulmak için bir anket yapılır. Telefonda 597 kişiye sorulduğunda A adayının 299 kişinin oyunu alacağı saptanmıştır. Basın durumu "A adayının avantajı hata payı \%4 içinde olduğu için o önde kabul edilebilir" diye rapor etmiştir. A oylarının hata payı hakikaten \%4'müdür?
n = 597.
k = 299
print n/2
print k/n
d = 0.98/np.sqrt(n)
print d*100
298.5
0.500837520938
4.01087299444
Evet hata payı \%4 çıktı.
Dikkat edilirse hata payının anketten gelen sonuçlarla hiçbir alakası yok, A için tercih \%25, \%75 olabilirdi ama üstteki hata payı hesabı yine aynı kalırdı. Bunun sebebi formülün $n$'ye bağlı olması.
Daha önemli soru hata payı basının üstteki ifadesinin gerçekten seçim sonucu ile alakalı olup olmadığı!
Hipotez Testleri (Hypothesis Testing)
İstatistik tek ya da aralıklar olarak sayısal tahminler üretmenin ötesinde, "iki şey arasında birisini seçmek" türünde bir karar bağlamında da kullanılabilir. Bir psikolog bir davaya uzman görüş vermek için çağrılmıştır ve sanık hakkında 'aklı olarak dengesiz ya da dengeli' arasında bir seçim yapacaktır. İlaç regülasyonu ile uğraşan kurum yeni bir ilaç hakkında 'etkili' ya da 'etkisiz' şeklinde bir karara ulaşacaktır.
Bir deneyin mümkün sonuçlarını belli seçeneklere yönlendirip olasılık teorisini kullanarak bunlardan birisini seçmeye İstatistik biliminde Hipotez Test Etmek adı verilir.
Birbiriyle yarış halinde olan iki hipotez vardır, bunlar sıfır hipotezi ($H_0$ olarak yazılıyor) ve alternatif hipotezdir ($H_1$ olarak yazılıyor). $H_o$ ve $H_1$ arasında nasıl seçim yapacağımız kavramsal olarak bir davada jürinin yaptığı seçime benzer: aynen sanığın, tersi ispatlanana kadar, masum kabul edilmesi gibi eğer veri tersi sonuca varmaya yetmezse $H_0$ da "kabul edilir", yani suçsuzluğun devam etmesi gibi $H_0$ görüşü terkedilmemiş olur. Statüko devam eder. Bu kararı verirken mahkemenin kanıtları incelemesi, hipotez testinde rasgele değişkenlerle verinin üzerinden hesaplar yapmaya benzer.
Bunu bir örnek üzerinden daha iyi anlayabiliriz. Diyelim ki araba üreten bir şirket yakıt performansını (gas mileage) arttırmaya uğraşıyor. Benzine katılan yeni bir madde üzerinde deneyler yapıyorlar, deney için Boston / Los Angeles arasında 30 tane araba sefer yapıyor. Yeni katkı maddesi olmadığı durumda (statüko) yakıt performansının ortalama 25.0 mil/galon ve standart sapmanın 2.4 mil/galon olduğu biliniyor. Diyelim ki deney sonrasında arabalar ortalama olarak $\bar{y}$=26.3 mil/galon performansı göstermişler. Katkı maddesi etkili mi, etkili değil mi?
Araştırmacılar 25.0'dan 26.3'e olan değişikliği daha önce bahsettiğimiz mahkeme örneğindeki gibi bir çerçevede incelerler. Tipik olarak sıfır hipotezi statükoyu temsil eder, yani değişmesi için "ezici şekilde aksi yönde veri olması gereken şey" budur. Öyle değil mi? Eğer etkisiz bir katkı maddesine evet dersek, ve ileride öyle olmadığı belli olursa bunun şirket için çok negatif etkileri olacaktır, aynen masum bir kişiyi yanlışlıkla hapse atmış olmak gibi. O yüzden kalmak istediğimiz güvenli konum $H_0$'i temsil etmelidir.
Bu noktada problemi rasgele değişkenlerin terminolojisi üzerinden tekrar tanımlamak faydalı olur. Diyelim ki test sırasında 30 tane aldığımız ölçüm $y_1,..,y_n$, her $y_i$ normal olarak dağılmış ve bu dağılımların $\mu$'şu aynı, ve $\mu$'u birazdan "eski" ölçümlerin ortalaması olarak alacağız, çünkü çürütmek istediğimiz hipotez bu. Ayrıca daha önceki tecrübelerimiz gösteriyor ki $\sigma = 2.4$. Yani,
$$ f_Y(y;\mu) = \frac{1}{\sqrt{2\pi}(2.4)} e^{-\frac{1}{2}(\frac{y-\mu}{2.4})^2}, -\infty < y < \infty $$
Hipotezleri şöyle tanımlayalım,
$H_0$: $\mu = 25.0$ (Katkı maddesi etkili değildir)
$H_0$: $\mu > 25.0$ (Katkı maddesi etkilidir)
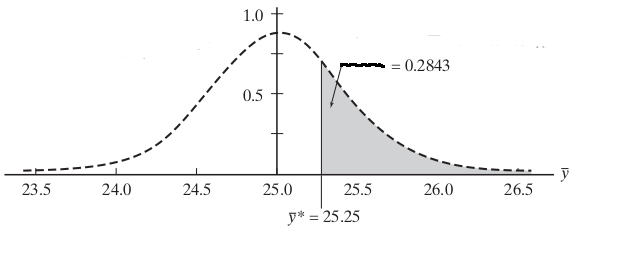
Şimdi yeni dağılımı standardize edip, bir hayali ortalama eşik değeri üzerinden bir sonuç çıkartalım, standardize etmek için kullandığımız $\mu = 25.0$ çünkü eski ortalama bu. Şimdi diyelim ki test ettiğimiz eşik değer 25.25 (esas amaç 26.3 ama oraya geleceğiz), aradığımız olasılık,
$$ P(\bar{Y} \ge 25.25) $$
Üstteki ifade "eğer örneklem eski dağılımdan geliyor olsaydı, 25.25 eşik değerini geçmesi ne kadar mümkün olabilirdi" diye bir soru soruyor. $\bar{Y}$'yi standardize edelim, o sırada eşitsizliğin sağ tarafı da değişir,
$$ P(\frac{\bar{Y} - 25.0}{2.4 / \sqrt{30}} \ge \frac{25.25 - 25.0}{2.4 / \sqrt{30}}) $$
$$ P(Z \ge 0.57)$$
z-Skoru tablosunu kullanakarak bu hesabı yapmak için
$$ 1 - P(Z < 0.57)$$
0.57'nin z-skoru (satır 0.5 kolon .07) 0.7157 olarak gösterilmiş, o zaman 1-0.7157 = 0.2843. Kod ile
print 1-norm.cdf(0.57)
0.284338849046
Demek ki
$$ P(Z \ge 0.57) = 0.2843$$
Demek ki yeni deney sonuçlarının, eski dağılıma göre, eşik değerinden fazla gelmesi hala az da muhtemel, demek ki eski hipotezi tam çürütemedik. Seçtiğimiz eşik değeri bize kesin bir sonuç sağlamadı, sezgisel olarak bu olasılığın büyük olduğunu görüyoruz. Mahkeme durumunda suçsuz olması çok muhtemeldir diyemiyoruz. Ya da araba örneğinde (ve pozitif bağlamda) yeni yakıt kesinlikle farklıdır / fazladır diyemiyoruz. Bize daha kesin noktalar lazım, aklımızda bize "acaba?" dedittirecek eşik değerler istemiyoruz.
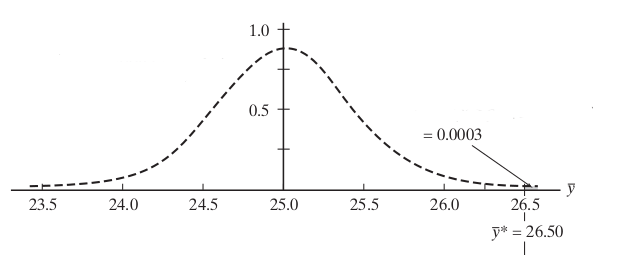
Hayali eşik noktası $\bar{y}^\ast$'nin daha büyük yapsak (ki o zaman ona bağlı olan sağdaki olasılık küçülecek). Bu olur mu? Eğer $\bar{y}^\ast = 26.50$ olsaydı?
$$ P(\frac{\bar{Y} - 25.0}{2.4 / \sqrt{30}} \ge \frac{26.50 - 25.0}{2.4 / \sqrt{30}}) $$
$$ P(Z \ge 3.42) $$
$$ = 0.0003 $$
Bu olasılık ise çok küçük, yani eşik değeri çok büyük! Çıtayı çok fazla kaldırdık, mahkeme durumunda sanki diyoruz ki suçun 1000 tane tanığı lazım, sanık suçunu itiraf etmiş olmalı, herşey apaçık olmalı, bir de herşeyi bizzat ben görmüş olmalıyım, yoksa kabul etmem. Araba örneğinde katkı maddesi arabaya Formula-1 yarısı kazandırmazsa biz bu yakıtı daha iyi olarak kabul etmeyiz diyoruz.
Peki eğer 0.28 çok fazla, 0.0003 çok küçük ise hangi olasılık en iyi eşik değerini verir? Bu soruya kesin olarak ve matematiksel bir cevap vermek mümkün değil, fakat hipotez test etme tekniğini kullanan araştırmacıların ulaştığı konsensüs 0.05 olasılık seviyesinin en iyi sonuçlar verdiğidir. Bu durumda sıfır hipotezinin çok kolayca kenara atılmaması, ya da ona gereğinden fazla bağlı kalınmaması mümkün oluyor.
O zaman 0.05 olasılığını verdirtecek eşik değeri hesaplayalım,
$$ P(\frac{\bar{Y} - 25.0}{2.4 / \sqrt{30}} \ge \frac{\bar{y}^\ast - 25.0}{2.4 / \sqrt{30}}) = 0.05 $$
$$ P(Z \ge \frac{\bar{y}^\ast - 25.0}{2.4 / \sqrt{30}}) = 0.05 $$ ya da
$$ P(Z \le \frac{\bar{y}^\ast - 25.0}{2.4 / \sqrt{30}}) = 0.95 $$
z-Skor tablosuna bakıyoruz, "hangi z değeri 0.95 değeri sonucunu verir", kordinatlardan 1.64 z-skorunu buluyoruz. Ya da
print norm.ppf(0.95)
1.64485362695
$$ P(Z \le 1.64) = 0.95 $$ O zaman
$$ \frac{\bar{y}^\ast - 25.0}{2.4 / \sqrt{30}} = 1.64 $$
ve buradan $\bar{y}^\ast = 25.178$ sonucu çıkıyor. 26.3 değeri bu değerden yüksektir demek ki sıfır hipotezi çürütülmüştür. Yeni yakıt katkısının performansı arttırıyor olması büyük bir olasılıktır.
Not: Bu testi aslında daha basit şekilde $\bar{y}^\ast = 26.3$ değerini vererek elde edilen değeri 0.05'ten küçük olup olmadığına bakarak ta yapabilirdik. Fakat metotu inşa ediyorduk o sebeple daha fazla örnekli anlatmak gerekti.
Örnek
SAT-I testinde ülke averajına oldukça yakın sonuçlar alan bir lisede yeni bir müfredat denenmesine karar veriliyor. Deneme için 86 öğrenci rasgele şekilde seçiliyor ve yeni bir tür cebir ve geometri dersine sokuluyor. Sonraki SAT-1 testinde sonuçlarına göre bu çocuklar ortalama 502 sonuç almışlar, ülke çapındaki ortalama 494, standart sapma 124. $\alpha=0.05$ önemliliği (significance) seviyesinde yeni müfredatın başarılı olduğu iddia edilebilir mi?
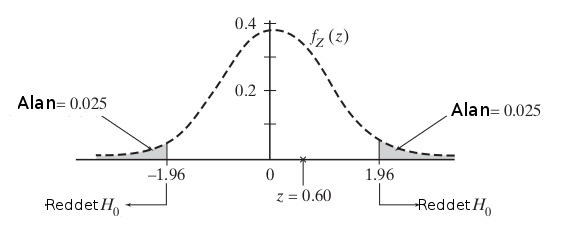
İlk önce $\mu$ parametresinin yeni müfredatın gerçek ortalaması olduğunu farzediyoruz. O zaman statüko nedir? Bu ortalamanın ülke ortalaması seviyesinde kalmasıdır, yani $\mu_0 = 494$ olmasıdır. Fakat bu sefer alternatif hipotez iki yönlü (two-sided) olmalı çünkü yeni müfredat, hiç istenmese de, test sonuçlarında negatif sonuca da yol açabilir! O zaman $H_0$'i reddetmeliyiz eğer z istatistiği $\le -z_{0.025}$ ise (yani -1.96'dan küçük ise), ya da $\ge z_{0.025}$ (yani 1.96'dan büyük ise).
$$ z = \frac{502-494}{124\sqrt{86}} = 0.60$$
Sonuç 1.96'dan büyük değil. O zaman $H_0$'i, yani statükoyu değiştiremedik. Elde edilen sonuçlar bir ilerlemedir fakat bu ilerlemenin şans eseri olması da muhtemel.
Binom Hipotez Testleri
Örnek
Erteleme Teorisi: Yaygın bir inanışa göre insanlar ölüm tarihlerini onlar için önemli bir gün sonrasına erteleyebiliyorlar, mesela kendi doğum günleri, aile toplantıları, bir akrabanın dönüşünü beklemek, vs. gibi Hatta ülke çapında seçimlerin bile ölüm günlerini etkilediği görülmüştür, başkanlık seçimleri olan Eylül ve Ekim ayları sırasında ölüm oranlarının düştüğü saptanmıştır. Bu teoriye göre pek çok yaşlı insan kimin kazandığını görmek için "biraz daha dayanıyor".
Bir araştırma bu teorinin doğru olup olmadığını kontrol etti. Bu bağlamda Salt Lake City şehrindeki bir gazetenin ölüm ilanı kısmına bakıldı ve 747 kişi içinden sadece 60 kişinin, daha doğrusu \%8'inin kendi doğumgünlerinin 3 ay öncesi içinde olduğunu saptadı. Eğer insanların ölümü rasgele olsaydı yaklaşık olarak \%25'inin bu periyod içinde ölmesini beklerdiniz. O zaman bu \%25'den \%8'e düşüşü nasıl açıklamalıyız? Araştırma teoriyi destekleyecek rakamları veriyor mu?
Diyelim ki 747 ölüm iki kategori üzerinden temsil edilsin, doğumgünü öncesindeki 3 ay içinde ölenler ve ölmeyenler. $k_i=1$ ile $i$'inci kişinin 1. kategoriye, $k_i=0$ ise 2. kategoriye ait olmasını temsil ediyoruz. O zaman $k = k_1 + k_2 + .. + k_{747}$ birinci kategorideki toplam ölümü temsil ediyor. Üstteki her $k$ doğal olarak Binom dağılımı, ve $p$ parametresini kullanıyor ki
$$ p = P(\textrm{sahıs doğumgünü öncesindeki 3 ay içinde ölüyor}) $$
Eğer insanlar ölümlerini ertelemeseydi $p = 3/12 = 0.25$ olurdu. Eğer erteliyorlar ise $p$ 0.25'den daha küçük olmalı. Bu azalmanın ne kadar önemli (significant) olduğunu irdelemek için tek taraflı bir Binom Testi uygulamak lazım.
$H_0$: $p = 0.25$
$H_1$: $p < 0.25$
Test için $p_0$ olduğunu farzettiğimiz "gerçek" dağılımı (ki statükoyu onun üzerinden temsil edeceğiz) kullanacağız.
$$ z = \frac{k-np_0}{\sqrt{np_0(1-p_0)}} \le -z_{0.05} = -1.64 $$
$$ = \frac{60-747(0.25)}{747(0.25)(0.75)} = -10.7 \le -1.64 $$
Test istatistiği kritik değerin aşırı derecede sol tarafına düştü. Demek ki ezici miktarda kanıt, veri, sonuç elde ettik, \%25'ten \%8'e düşüşün pür şans dışında başka bir sebebi var. Tabii bu sebep Erteleme Teorisi haricinde bir şey de olabilir, fakat yine de ortaya çıkan kalıp bize ölüm vaktimizin kontrolümüzde olduğunu destekleyen yönde bir sonuç veriyor.
Not: Üstteki test "büyük örneklem" olduğu durumlarda geçerlidir. Küçük örneklem durumunda Binom dağılımının kendisi test için kullanılabilir.
Tek Örneklem t Testi (The One-Sample t test)
Bu test verinin bir $N(\mu,\sigma)$ Normal dağılımından geldiğini farzeder, test etmek istediğimiz hipotez / karşılaştırma $\mu = \mu_0$. Ayrıca $\sigma$ bilinmiyor, ki Öğrenci t dağılımından bahsetmemizin ana sebebi buydu zaten, o zaman hipotez testine Tek Örneklem t Testi adı verilir.
Örnek
Alttaki veride bir grup hanımın ne kadar kalori tükettiği kayıtlanmış. Acaba bu hanımların aldığı enerji tavsiye edilen 7725'ten ne kadar sapmıştır?
daily_intake = np.array([5260.,5470.,5640.,6180.,6390.,6515.,6805.,\
7515.,7515.,8230.,8770.])
Örneklem küçük. O sebeple t dağılımı kullanmak mantıklı. t değerini $\frac{\bar{y}-\mu_o}{s/\sqrt{n}}$ olarak hesaplayacağız, ki $\mu_0=7725$ olacak.
from scipy.stats.distributions import t
import pandas as pd, math
data = pd.DataFrame(daily_intake)
n = len(data)
df = n-1 # serbestlik derecesi
mu0 = 7725.
ybar = float(data.mean())
s = float(data.std())
print 'ortalama',ybar,'std',s
tval = (ybar-mu0)/(s/np.sqrt(n))
print 'df',df,'tval',tval
print 'sol',t.ppf(0.025,df)
print 'sag',t.ppf(0.975,df)
ortalama 6753.63636364 std 1142.12322214
df 10 tval -2.82075406083
sol -2.22813885196
sag 2.22813885196
Sol ve sağ eşik değerlerini hesapladık ve t değeri bu aralığın içine düşmüyor. Yani hipotezi reddediyoruz. Bazıları bu problemde p değeri görmek isteyebilir,
print 't degeri', tval
print 'iki tarafli p degeri', 2*t.cdf(tval,df)
t degeri -2.82075406083
iki tarafli p degeri 0.0181372351761
p değeri hesapladık 0.05'ten küçük çıktı. İkiyle çarpmamızın sebebi iki-taraflı p-testi yapmış olmamız, yani kabul edilebilir bölgenin hem solundan hem de sağından ne kadar dışına düşüyorsak, bu iki taraftaki p değerini birbirine toplamalıyız. Tabii t dağılımı simetrik olduğu için her iki taraftan da aynı şekilde dışarıda kalıyoruz. Bazı kaynaklar iki taraflı p testinin $|t| < -t_{esik,derece}$ karşılaştırmasını yaptığını söyler.
Benzer bir hesabı kütüphane çağrısı ile yaparsak,
from scipy.stats import ttest_1samp
t_statistic, p_value = ttest_1samp(daily_intake, mu0)
print 't', t_statistic, 'one-sample t-test', p_value
t -2.82075406083 one-sample t-test 0.0181372351761
Sonuç p değeri 0.05'ten küçük çıktı yani yüzde 5 önemliliğini (significance) baz aldık bu durumda veri hipotezden önemli derecede (significantly) uzakta. Demek ki ortalamanın 7725 olduğu hipotezini reddetmemiz gerekiyor.
İki Örneklemli Test
Gruplar 0/1 değerleri ile işaretlendi, ve test etmek istediğimiz iki grubun ortalamasının (mean) aynı olduğu hipotezini test etmek. t-test bu arada varyansın aynı olduğunu farzeder.
energ = np.array([
[9.21, 0],[7.53, 1],
[7.48, 1],[8.08, 1],
[8.09, 1],[10.15, 1],
[8.40, 1],[10.88, 1],
[6.13, 1],[7.90, 1],
[11.51, 0],[12.79, 0],
[7.05, 1],[11.85, 0],
[9.97, 0],[7.48, 1],
[8.79, 0],[9.69, 0],
[9.68, 0],[7.58, 1],
[9.19, 0],[8.11, 1]])
group1 = energ[energ[:, 1] == 0][:, 0]
group2 = energ[energ[:, 1] == 1][:, 0]
t_statistic, p_value = ttest_ind(group1, group2)
print "two-sample t-test", p_value
two-sample t-test 0.00079899821117
$p$ değeri $< 0.05$ yani iki grubun ortalaması aynı değildir. Aynı olduğu hipotezi reddedildi.
Eşlemeli t-Test (Paired t-test)
Eşlemeli testler aynı deneysel birimin ölçümü alındığı zaman kullanılabilir, yani ölçüm alınan aynı grupta, deney sonrası deneyin etki edip etmediği test edilebilir. Bunun için aynı ölçüm deney sonrası bir daha alınır ve "farkların ortalamasının sıfır olduğu" hipotezi test edilebilir. Altta bir grup hastanın deney öncesi ve sonrası ne kadar yiyecek tükettiği listelenmiş.
intake = np.array([
[5260, 3910],[5470, 4220],
[5640, 3885],[6180, 5160],
[6390, 5645],[6515, 4680],
[6805, 5265],[7515, 5975],
[7515, 6790],[8230, 6900],
[8770, 7335],
])
pre = intake[:, 0]
post = intake[:, 1]
t_statistic, p_value = ttest_1samp(post - pre, 0)
print "paired t-test", p_value
paired t-test 3.05902094293e-07
Wilcoxon işaretli-sıralı testi (Wilcoxon signed-rank test)
t Testleri Normal dağılıma göre sapmaları yakalamak açısından, özellikle büyük örneklemler var ise, oldukça sağlamdır. Fakat bazen verinin Normal dağılımdan geldiği faraziyesini yapmak istemeyebiliriz. Bu durumda dağılımdan bağımsız metotlar daha uygundur, bu tür metotlar için verinin yerine çoğunlukla onun sıra istatistiklerini (order statistics) kullanır.
Tek örneklemli Wilcoxon testi için prosedür $\mu_0$'i tüm veriden çıkartmak ve
geri kalan (farkları) işaretine bakmadan sayısal (numeric) değerine göre
sıralamak, ve bu sıra değerini bir kenara yazmak. Daha sonra geri dönüp bu sefer
çıkartma işlemi sonucunun işaretine bakmak, ve eksi işareti taşıyan sıra
değerlerini toplamak, aynı işlemi artı işareti için yapmak, ve eksi toplamı artı
toplamından çıkartmak. Sonuçta elimize bir istatistik $W$ gelecek. Bu test
istatistiği aslında $1..n$ tane sayı içinden herhangi birini $1/2$ olasılığıyla
seçmek, ve sonuçları toplamaya tekabül etmektedir. Ve bu sonuç yine 0.05
ile karşılaştırılır.
from scipy.stats import wilcoxon, ttest_ind
daily_intake = np.array([5260,5470,5640,6180,6390,6515,6805,7515,7515,8230,8770])
z_statistic, p_value = wilcoxon(daily_intake - 7725)
print "one-sample wilcoxon-test", p_value
one-sample wilcoxon-test 0.0279991628713
Hipotezi reddettik.
Eşlemeli t-testi şimdi Wilcoxon testi ile yapalım,
z_statistic, p_value = wilcoxon(post - pre)
print "paired wilcoxon-test", p_value
paired wilcoxon-test 0.00463608893545
Normallik Testi
Paket scipy.stats altında normallik testleri için bazı çağrılar var,
bu tekniklerden ikisini altta gösteriyoruz,
import scipy.stats as st
arr = np.array([3,4,3,10,10,444,444,3,98])
arr2 = np.array([np.random.normal() for i in range(100)])
print 'D-Agostino and Pearsons'
print st.normaltest(arr)
print st.normaltest(arr2)
print
print 'Shapiro-Wilk'
print st.shapiro(arr)
print st.shapiro(arr2)
D-Agostino and Pearsons
(4.6919700569024814, 0.095752836393526289)
(1.4265636263795889, 0.49003335773235424)
Shapiro-Wilk
(0.6167718172073364, 0.00015052134403958917)
(0.9891485571861267, 0.5962899923324585)
Sonuçlara göre Shapiro-Wilk yaklaşımı daha güvenilir gözüküyor, zaten [6, sf 53]'e göre örneklem sayısı $\le 50$ olduğu durumlarda bu test tercih edilmelidir.
Biraz Matematik
Diyelim ki Gaussian dağılımına sahip olduğunu düşündüğümüz ${ x_i}$ verilerimiz var. Bu verilerin Gaussian dağılımına uyup uymadığını nasıl kontrol edeceğiz? Normal bir dağılımı her veri noktası için şöyle temsil edebiliriz,
$$ y_i = \Phi\bigg(\frac{ x_i - \mu}{\sigma}\bigg) $$
Burada $\Phi$ standart Gaussian'ı temsil ediyor (detaylar için [7] ve CDF fonksiyonuna tekabül ediyor. CDF fonksiyonunun aynı zamanda yüzdelik dilimi (quantile) hesapladığı söylenir, aslında CDF son derece detaylı bir olasılık değeri verir fakat evet, dolaylı yoldan noktanın hangi çeyrek içine düştüğü de görülecektir.
Şimdi bir numara yapalım, iki tarafa ters Gaussian formülünü uygulayalım, yani $\Phi^{-1}$.
$$ \Phi^{-1}(y_i) = \Phi^{-1}\bigg( \Phi\bigg(\frac{ x_i - \mu}{\sigma}\bigg)\bigg) $$
$$ \Phi^{-1}(y_i) = \frac{ x_i - \mu}{\sigma}$$
$$ x_i = \Phi^{-1}(y_i) \sigma + \mu $$
Bu demektir ki elimizdeki verileri $\Phi^{-1}(y_i)$ bazında grafiklersek, bu noktalar eğimi $\sigma$, kesisi (intercept, y ekseninin kesildiği yer) $\mu$ olan bir düz çizgi olmalıdır. Eğer kabaca noktalar düz çizgi oluşturmuyorsa, verimizin Gaussian dağılıma sahip olmadığına karar verebiliriz.
Üstte tarif edilen grafik, olasılık grafiği (probabılıty plot) olarak bilinir.
Ters Gaussian teorik fonksiyonunu burada vermeyeceğiz, Scipy
scipy.stats.ınvgauss hesaplar için kullanılabilir. Fakat $y_i$'nin
kendisi nereden geliyor? Eğer $y_i$, CDF'in bir sonucu ise, pür veriye
bakarak bir CDF değeri de hesaplayabilmemiz gerekir. Bunu yapmak için bir
başka numara lazım.
-
Eldeki sayıları artan şekilde sıralayın
-
Her veri noktasına bir derece (rank) atayın (sıralama sonrası hangi seviyede olduğu yeterli, 1'den başlayarak).
-
Çeyrek değeri $y_i$ bu sıra / $n+1$, $n$ eldeki verinin büyüklüğü.
Bu teknik niye işliyor? $x$'in CDF'i $x_i < x$ şartına uyan $x_i$'lerin oranı değil midir? Yani bir sıralama söz konusu ve üstteki teknik te bu sıralamayı biz elle yapmış olduk, ve bu sıralamadan gereken bilgiyi aldık.
Basit bir Gaussian kontrolü, qqplot kullanarak.
import statsmodels.api as sm
fig = sm.qqplot(arr)
plt.savefig('stat_tests_01.png')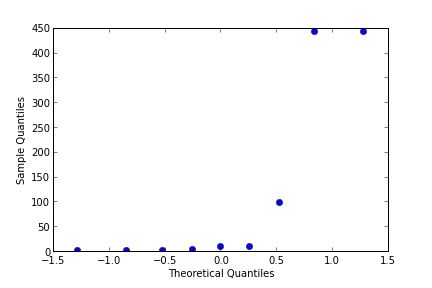
Gerçekten Gaussian olan bir veri şöyle gözükür,
fig = sm.qqplot(arr2)
plt.savefig('stat_tests_02.png')
Kaynaklar
[1] Dalgaard, Introductory Statistics with R
[2] Kerns, Introduction to Probability and Statistics Using R
[3] Blondel, t-test and wilcoxon-test examples in Python, url{https://gist.github.com/mblondel/1761714}
[4] Runger, Applied Statistics and Probability for Engineers
[5] Stack Exchange, Sample variance converge almost surely, http://math.stackexchange.com/questions/243348/sample-variance-converge-almost-surely
[6] Haslwanter, Introduction to Statistics using Python
[7] Bayramlı, İstatistik, Giris)
[8] Bayramlı, Istatistik, Örneklem Büyüklüğü
Yukarı