Diyelim ki \(X_1,..,X_i\) örneklemi birbirinden bağımsız, aynı dağılımlı ve ortalaması \(\mu\), standart sapması \(\sigma\) ve yine aynı olan bir nüfus dağılımından geliyor. O zaman biliyoruz ki, Merkezi Limit Teorisi (Central Limit Theorem) teorisine göre, \(n\) arttıkça örneklem ortalaması \(\bar{X} = \frac{1}{n} X_1+..+X_n\), ortalaması \(\mu\), standart sapması \(\sigma/n^2\) olan bir normal dağılıma yaklaşıyor.
Peki veriyi (yani örneklemi) ve CLT’yi kullanarak \(\mu\) hakkında bir tahmin yapabilir miyiz? Yani Büyük Sayılar Kanunua göre \(\mu\) hakkında noktasal tahmin yapabiliriz fakat, belki ondan bir adım ötesi, bir “güven aralığı’’ hesaplamaktan bahsediyoruz. Bu tahmin”gerçek \(\mu\), %95 ihtimalde şu iki değer arasındadır’’ türünde bir tahmin olacak.
Dikkat: burada verinin yüzde kaçının belli bir aralıkta olup olmadığından bahsetmiyoruz, tahminsel hesabı yapılan ortalamanın hangi güven seviyesinde bir aralıkta olup olmadığından bahsediyoruz. Verinin güven aralığı hakkındaki notlar bu yazının sonunda.
Bu aralığın hesabı için önce \(\bar{X}\)’i standardize edelim, yani \(N(0,1)\) haline çevirelim,
\[ Z = \frac{\bar{X} - \mu}{\sigma / \sqrt{n}} \]
Z-skorlarını işlediğimiz yazıda
\[ P(z_1 < Z < z_2) = \Phi(z_1) - \Phi(z_2) \]
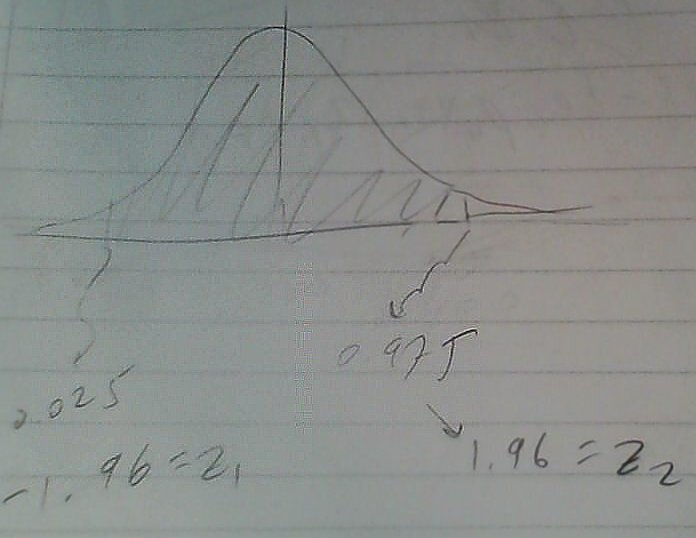
gibi bir ifade gördük. Eşitliğin sağ tarafı aslında bir alan hesabıdır, sürekli fonksiyonlarda olasılık bir entegral, ya da iki kümülatif yoğunluk fonksiyonunun farkı. Güven aralığı için bize lazım olan da bir olasılık, hatta “kesin’’ bir olasılık, %95 olasılığı. Demek ki eşitliğin sağ tarafı .95 olacak. .95 hesabı için, normal eğrisini düşünürsek, sağından ve solundan 0.25 büyüklüğünde iki parçayı”kırpmamız’’ lazım. O zaman 0.975 olasılığının z değeri ile, 0.025 olasılığının z değeri arasındaki olasılıkta olmamız lazım. Bu hesaplarda baz alınan \(z_{\alpha/2}\) değeri ve bu \(100 \cdot \alpha / 2\) üst yüzdelik kısmına, örneğimizde 0.975 kısmına tekabül ediyor. Normal dağılımın simetrisi sebebiyle onun eksisi alınmış hali öteki (soldaki) parçayı verir, yani \(-z_{\alpha/2}\).

Z-skoru hesaplarken tabloya danışmıştık, şimdi tabloya tersinden bakacağız, kesişme noktasında 0.975 diyen yeri bulup kordinatları alacağız, ki bu değer 1.96.
from scipy.stats.distributions import norm
print (norm.ppf(0.975))1.95996398454Bazı İstatistik kaynaklarında “sihirli değer’’ şeklinde tarif edilen bir değer bu, gözlerimiz kamaşmasın, geldiği yer burası işte. Şimdi formülü buna göre değiştirelim,
\[ P \bigg( -z_{\alpha/2} \ \le \frac{\bar{X} - \mu}{\sigma / \sqrt{n}} \le z_{\alpha/2} \bigg) = 1-\alpha \]
\(P(\cdot)\) içinde biraz düzenleme, tüm terimleri \(\sigma / \sqrt{n}\) ile çarpalım, \(\bar{X}\) çıkartalım, ve \(-1\) ile çarpalım,
\[ P \bigg( \bar{X} - z_{\alpha/2}\frac{\sigma}{\sqrt{n}} \le \mu \le \bar{X} + z_{\alpha/2}\frac{\sigma}{\sqrt{n}} \bigg) = 1-\alpha \qquad (1) \]
Güven aralığı ifadesine aslına erişmiş olduk. Eğer %95 kesinlikten bahsediyor olsaydık, ve nüfusun gerçek varyansı \(\sigma^2\) biliniyor olsaydı, \(P(\cdot)\) içine bu değerleri geçecektik, \(\bar{X}\) zaten verinin aritmetik ortalamasından ibarettir, bu bize \(\mu\)’nun solunda ve sağında bazı değerler döndürecekti. Bu değerler bizim güven aralığımız olacaktı. Mesela veri 64.1, 64.7, 64.5, 64.6, 64.5, 64.3, 64.6, 64.8, 64.2, 64.3 şeklinde, \(n=10\) çünkü 10 nokta var, \(\sigma = 1\) olarak verilmiş. Ortalamayı hesaplıyoruz, 64.46. \(\alpha=0.05\) için
\[ P \bigg( 64.46 - 1.96\frac{1}{\sqrt{10}} \le \mu \le 64.46 + 1.96\frac{1}{\sqrt{10}} \bigg) = 0.95 \]
\[ P\bigg(63.84 \le \mu \le 65.08\bigg) = 0.95 \]
Yani %95 güven aralığı \(63.84 \le \mu \le 65.08\).
Neler yaptık? CLT bilgisinden hareketle \(\bar{X}\) hakkında bir şeyler biliyorduk. Fakat \(\bar{X}\)’in kesin hangi normal dağılıma yaklaştığını bilmek için nüfus paremetreleri \(\mu,\sigma\) da bilinmelidir. Diğer yandan eğer tek bilinmeyen \(\mu\) ise, teoriyi bu bilinmez etrafında tamamen tekrar şekillendirip / değiştirip CLT’yi bilinmeyen \(\mu\) etrafında bir güven aralığı yaratmak için kullandık.
Not: Eğer \(\sigma\) bilinmiyor ise onu da veriden hesaplarız, \(S^2\) tahmin edicisi ile, yanlız bu durumda \(S^2\) te bir dağılıma sahip olacaktır, \(\chi^2\) dağılımı, ve üstte \(P()\) içindeki bölüm bir Normal rasgele değişkeni bolu \(\chi^2\) bölümü haline gelir, ki bu bölüm Öğrenci t dağılımı adında başka bir dağılıma sahiptir! O zaman üstteki cebirsel hareketleri bunu hesaba katarak yapmak gerekir. Bunun detaylarını ilerideki bir bölümde göreceğiz.
Kac Tane \(n\)?
Hatırlarsak güven aralığını üstteki şekilde hesaplayabilmemizin sebebi CLT sayesinde \(\bar{X}\)’in normal dağılıma yaklaşıyor olmasıydı. Ve, teoriyi tekrar düşünürsek yaklaşma \(n \to \infty\) olduğu zaman oluyordu. Buradan \(\bar{X}\)’in normalliğinin “büyükçe’’ \(n\) değerleri için daha geçerli olacağı sonucuna varabiliriz. Peki \(n\) ne kadar büyük olmalı? Literatüre göre CLT’nin genellikle \(n \ge 30\) durumunda geçerli olduğu söylenir. Tabii nüfus dağılımının ne olduğu da önemlidir, eğer nüfus normal ise, ya da genel olarak simetrik tek tepeli dağılım ise örneklem daha ufak kalsa da bazı sonuçlara varabiliriz. Eğer nüfus dağılımı çok yamuk (skewed), etekleri geniş dağılım ise o zaman daha büyük örneklem daha iyi olur.
Soru
İÖ 800 yıllarında İtalya’da Etrusyalı (Etruscan) toplumu vardı, bilinmeyen bir sebeple bu insanlar geldikleri gibi birdenbire ortadan kayboluverdiler. Bilimciler bu toplumun İtalyalılar ile fizyolojik, genetik ve kültürel olarak bağlantısı olup olmadığını hep merak etmiştir. Bazıları hafa ölçülerine bakarak sonuçlara varmaya uğraşmıştır. Arkeolojik kazılarda yapılan ölçümlerde 84 Etrusyalının kafası ölçülmüştür. Ayrıca bugünkü İtalyanların kafa ölçümlerinin normal dağılımda \(\mu=132.4 mm,\sigma=6.0mm\) olduğu bilinmektedir. İki toplum arasındaki bağlantı kurmak için, veriye bakarak kafa ölçümü ortalaması için bir %95 güvenlik aralığı oluşturabiliriz, ve eğer bugünkü İtalyanların ölçüsü o aralığa düşmüyorsa, Etrusyalılarla bağlantılarının olmadığını iddia edebiliriz.
import pandas as pd
dfetr = pd.read_csv('../stat_035_tests/etrus.csv')
print (float(dfetr.mean()-1.96*(6.0/np.sqrt(84))))
print (float(dfetr.mean()+1.96*(6.0/np.sqrt(84))))142.524107721075
145.09035011025028Bugünkü İtalyanların kafa ortalaması \(\mu=132.4\) bu aralığa düşmüyor. Diğer bir deyişle, 84 tane örneklemden gelen örneklem ortalaması 143.8 büyük bir ihtimalle \(\mu=132.4,\sigma=6.0\) boyutlarındaki bir normal dağılımdan gelmemiştir. Buna göre, büyük bir ihtimalle Etrusyalılar İtalyanların atası değildir.
Bilinmeyen \(\sigma\)
Güven Aralıkları bölümünden devam edelim. Bilinmeyen \(\mu\) durumunu gördük. Eğer \(\sigma\) bilinmiyorsa, bu durumda \(\sigma\) yerine örneklem varyansı \(S\) kullanılabilir,
\[ S^2 = \frac{1}{n} \sum (X_i - \bar{X})^2 \]
ki üstteki değerin karekökü \(S\) olacaktır. \(\sigma\) yerine \(S\) kullanmanın büyük \(n\) değerlerinde CLT’yi etkilemediği ispat edilmiştir [5]. Fakat daha küçük örneklem durumunda t Dağılımı daha uygun olur.
T Dağılımı
Daha önce Z oranını temel alarak güven aralıkları ya da hipotez testleri oluşturmuştuk. Bu işlemler için standart normal dağılımın üst ve alt yüzdelikleri hakkında bazı bilgiler gerekmişti. Bu bilgiler bir tablodan bakılan değerlerdi ya da istatistik yazılımımızda gerekli bir çağrı ile hemen bulunabiliyorlardı.
Öğrenci t’nin Z’ye göre farklı bir tarafı belli bir değeri bulmak için iki parametreye ihtiyaç olması, bunlardan biri \(\alpha\) diğeri ise serbestlik derecesi (degree of freedom -dof-). Standart normal için tablo paylaştık, fakat t için artık tablolarla uğraşmayacağız, bilgisayar çağındayız, yazılım ile bu işi halledelim!
Örnek
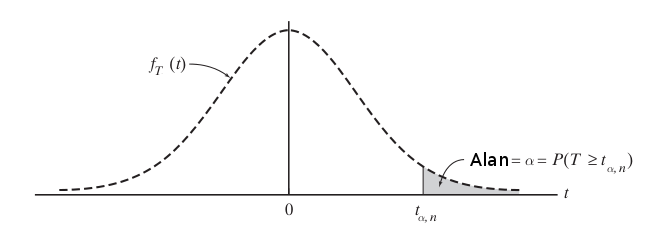
\(T\) bir Öğrenci t dağılımı ise, ve serbestlik derecesi 3 ise, \(\alpha=0.01\) için için \(f_T(t)\)’nin \(100(1-\alpha)\) yüzdeliği nedir? Üstteki grafikteki \(t_{\alpha,n}\) notasyonundan hareketle \(t_{0.01,3}\) değerini arıyoruz yani.
from scipy.stats.distributions import t
df = 3
print (t.ppf(0.99,df))
print (1-t.cdf(4.541,df))4.5407028587
0.00999823806449Yani
\[ P(T_3 \ge 4.541) = 0.01 \]
\(\frac{\bar{Y}-\mu}{S/\sqrt{n}}\) ifadesinin n-1 derece serbestliğe sahip Öğrenci t dağılımına sahip olduğunu bilmek alttaki ifadeyi mümkün kılar,
\[ P \bigg( -t_{\alpha/2,n-1} \le \frac{\bar{Y}-\mu}{S/\sqrt{n}} \le t_{\alpha/2,n-1} \bigg) = 1-\alpha \]
Bu ifadeyi daha önce standart normal için yaptığımız gibi tekrar düzenlersek,
\[ P \bigg( \bar{Y}-t_{\alpha/2,n-1}\frac{S}{\sqrt{n}} \le \mu \le \bar{Y}+t_{\alpha/2,n-1}\frac{S}{\sqrt{n}} \bigg) = 1-\alpha \]
Tabii, \(Y_i\)’ların normal dağılımdan gelmiş olması lazım. Bunun sonucunda gerçek veri temel alınarak hesaplanacak \(S\) ve \(\bar{Y}\) bize \(\mu\) için bir \(\%100(1-\alpha)\) güven aralığı verecektir.
Örnek
Yapışkan elementlerin üzerinde yapılan deneyler sonucundaki ölçümler altta verilmiştir. Acaba \(\mu\) için %95 güven aralığı nedir?
Öncelikle verinin normal dağılımdan geldiği doğru mudur? Bu faraziyeyi kontrol etmemiz gerekir yoksa t dağılımını kullanamayız. Önce bir kutu grafiği (boxplot) yapalım,
data = np.array([19.8,10.1,14.9,7.5,15.4,15.4,15.4,18.5,7.9,12.7,
11.9,11.4,11.4,14.1,17.6,16.7,15.8,19.5,8.8,13.6,11.9,11.4])
plt.boxplot(data)
plt.savefig('stat_ci_01.png')
Şimdi normal olasılık grafiği (normal probability plot) yapalım, ki bu grafik verinin normal dağılıma ne kadar uyumlu olduğunu grafik olarak gösterir, eğer uyumlu ise veri düz çizgiye yakın çıkmalıdır,
import scipy.stats as stats
res = stats.probplot(data, plot=plt)
plt.savefig('stat_ci_02.png')
Bu grafiklere bakınca verinin normal olduğu belli oluyor. Zaten örneklem sayısı az, bu sebeple t dağılımı kullanmak uygun. Veri sayısal ortalaması ve sayısal standart sapmasına bakalım, ve güven aralığını hesaplayalım, yani
\[ \bar{x} - t_{\alpha/2,n-1}s/\sqrt{n} \le \mu \le \bar{x} + t_{\alpha/2,n-1}s/\sqrt{n} \]
from scipy.stats.distributions import t
n = len(data)
dof = len(data)-1
m = np.mean(data)
s = np.std(data)
print ('ortalama',m)
print ('sapma',s)
print (m + t.ppf(0.025,dof) * s / np.sqrt(n),\
m - t.ppf(0.025,dof) * s / np.sqrt(n))ortalama 13.7136363636
sapma 3.47187340764
12.174293931 15.2529787962Güven aralığı oldukça geniş, çünkü (demek ki) ölçümlerde yüksek değişkenlik var.
Normal Nüfusun Varyansının Güvenlik Aralığı
Bazen nüfusun varyansı ya da standart sapması üzerinde bir güven aralığı hesaplamak gerekebilir. Eğer nüfus normal olarak dağılmış ise, şimdiye kadar gösterdiğimiz tekniklerin hepsi kullanılabilir. (1) teorisinin b kısmındaki ifadeyi kullanırsak, nüfusu \(\mu,\sigma\) parametreli bir normalden alınan \(X_1,..,X_n\) örneklemi üzerinden hesaplanan \(X^2 = \frac{(n-1)S^2}{\sigma^2}\) ifadesinin \(n-1\) serbestlik derecesindeki bir chi kare dağılımı olduğunu biliyoruz.
Chi karenin yüzdelik kısımları altta görülebilir,

from scipy.stats.distributions import chi2
print (chi2.ppf(0.05,5))
print (chi2.ppf(0.99,5))1.14547622606
15.0862724694Dikkat edilmesi gereken bir konu chi karenin yamuk (skewed) olması sebebiyle sağdaki ve soldaki alan hesaplarının arasında z skorunda olduğu gibi her seferinde birebir geçiş yapılamayabileceği.
Notasyonel olarak \(\chi_{p,n}^2\) ifadesi, x eksenindeki bir eşik noktasını ifade eder ki bu değerin sol tarafındaki alan büyüklüğü \(p\), \(n\) serbestlik derecesindeki chi kare dağılımının alanıdır. Mesela üstte \(\chi_{0.05,5}^2 = 1.145\) ve \(\chi_{0.99,5}^2 = 15.086\). Olasılık ifadesi olarak
\[ P(\chi_5^2 \le 1.145) = 0.05 \]
\[ P(\chi_5^2 \le 15.086) = 0.05 \]
Not: Bazı kaynaklar eşik değerinin sağ kısmını referans alıyor her nedense, bu duruma dikkat.
\(\sigma^2\) İçin Güvenlik Aralığı
Chi kare tanımından hareketle şu ifadeyi yazabiliriz,
\[ P\bigg( \chi_{\alpha/2,n-1}^2 \le \frac{(n-1)S^2}{\sigma^2} \le \chi_{1-\alpha/2,n-1}^2 \bigg) = 1-\alpha \]
Belirtildiği üzere, üstteki ifadenin \(Z\)’li halinde olduğu gibi, bir z değerini alıp, eksi ile çarparak (ve çarpmayarak) hem sol hem sağda eşik değeri olarak kullanamadık çünkü chi kare simetrik değil. Eşik değerinin belli noktalarda ayrı ayrı hesaplanması gerekiyor.
Üstteki denklem birkaç cebirsel işlem sonrasında \(\sigma^2\)’yi ortada tek başına bırakacak şekilde değiştirilebilir, önce eşitsizlikleri tersine çeviriyoruz, aynı anda ortadaki bölüme tersine çeviriyoruz, ve yeni böleni hem sol hem sağa çarparak taşıyoruz,
\[ P \bigg( \frac{(n-1)S^2}{\chi_{1-\alpha/2,n-1}^2} \le \sigma^2 \le \frac{(n-1)S^2}{\chi_{\alpha/2,n-1}^2} \bigg) = 1-\alpha \]
Eşitsizliğin karekökünü alırsak, \(\sigma\) için \(\%100(1-\alpha)\) güven aralığı
\[ \bigg( \sqrt{\frac{(n-1)S^2}{\chi_{1-\alpha/2,n-1}^2}} , \sqrt{\frac{(n-1)S^2}{\chi_{\alpha/2,n-1}^2}} \bigg) \]
Örnek
Bir fabrikada deterjanları doldurmak için bir makina kullanılıyor. Rasgele seçilen bir örneklemde 20 tane deterjan plastik şişeden alınan ölçümlerde örneklem varyansının \(s^2 = 0.0153\) olduğu hesaplanıyor (birim \(ons^2\)). Bu ölçümlerin standart sapması \(\sigma^2\) için %95’lik üst güven sınırı nedir?
\[ \sigma^2 \le \sqrt{\frac{(19)0.0153}{\chi_{0.05,19}^2}} \]
from scipy.stats.distributions import chi2
print (chi2.ppf(0.05,19))10.1170130639\[ \sigma^2 \le \sqrt{\frac{(19)0.0153}{10.117}} = 0.0287 \]
Yani
\[ \sigma \le 0.17 \]
Demek ki nüfusun gerçek standart sapması 0.17 ons kadar büyük olabilir.
Nüfus Ortalama Farkı, \(\mu_1-\mu_2\) Güven Aralığı
İki farklı nüfusun ortalamaları \(\mu_1,\mu_2\)’nin birbirinden farklı olup olmadığını, ve bu farkın istatistiki önemli olup olmadığını nasıl anlarız? Bir yaklaşım, iki nüfusun örneklem ortalaması \(\bar{X}_1,\bar{X}_2\)’i kullanmak ve farklılık \(\mu_1-\mu_2\)’ için bir güven aralığı oluşturmak, eğer sıfır değeri bu aralık içine düşüyorsa, farklılık vardır. Birbirinden aynı olan şeylerin farkı sıfır olduğuna göre eğer sıfır güven aralığı içinde ise bu iki nüfusun ortalamasının birbirine yakın olduğundan emin olabiliriz.
Devam edelim; Merkezi Limit Teorisi’ne göre yeterince büyük örneklemler, yani \(n_1>30,n_2>30\) için, \(\bar{X}_1,\bar{X}_2\) Normal olarak dağılmaya mecbur.
Diğer yandan biliyoruz ki iki Normal dağılımın toplamı, ya da çıkartılması yeni bir Normal dağılım verir. \(\mu_a,\mu_b\) ve \(\sigma_a,\sigma_b\) için, toplam \(N(\mu_a+\mu_b, \sigma_a+\sigma_b)\) elde edilir. Örneklem durumunda ve çıkartma sonrası yeni ortalama ve standart sapma
\[ \mu_1-\mu_2, \qquad \frac{\sigma_1^2}{n_1} + \frac{\sigma_2^2}{n_2}\]
olacaktır [1, sf. 257].
Ayrıca \(\mu\) ortalamasına, \(\sigma\) varyansına sahip bir \(\bar{X}\)’i
\[ Z = \frac{\bar{X}-\mu}{\sigma/\sqrt{n}} \]
ile standart normal \(Z = N(0,1)\)’e cevirilebileceğimizi biliyoruz.
O zaman yaklaşım şöyle olabilir; \(\bar{X}_1-\bar{X}_2\)’i hesaplarız, bu dağılımın kesinlikle normal olduğunu biliyoruz; o zaman nüfus ortalama ve standart sapması üzerinden standardizasyon ve biraz cebirsel cambazlık ile \(\mu_1-\mu_2\) için bir güven aralığı oluştururuz.
\[ Z = \frac{\bar{X}_1-\bar{X}_2 - (\mu_1-\mu_2)} {\sqrt{\sigma_1^2/n_1 + \sigma_2^2/n_2}} \]
\[ P \bigg( -z_{\alpha/2} \le \frac{\bar{X}_1-\bar{X}_2 - (\mu_1-\mu_2)} {\sqrt{\sigma_1^2/n_1 + \sigma_2^2/n_2}} \le z_{\alpha/2} \bigg) = 1-\alpha \]
\[ P[ (\bar{X}_1 - \bar{X}_2) - z_{\alpha/2}\sigma_w \le \mu_1-\mu_2 \le (\bar{X}_1 - \bar{X}_2) + z_{\alpha/2}\sigma_w ] = 1-\alpha \]
ki \(\sigma_w = \sqrt{\sigma_1^2/n_1 + \sigma_2^2/n_2}\). Eğer \(\sigma\) bilinmiyorsa, onun yerine, yine yeterince büyük örneklem için örneklem standart sapması \(s\) kullanılabilir.
\(\sigma^2\) için yansız (unbiased) tahmin edici
\[ s^2 = \sigma_i (X_i-\bar{X})^2 / (n-1) \]
Not: Kaynaklarda çoğunlukla \(\sigma^2\) yerine \(s^2\) kullanılırsa \(Z\) yerine \(T\) yani Öğrenci T dağılımı kullanılması tavsiye edilir, fakat eğer örneklem yeterince büyük ise \(Z\) kullanımında problem yoktur [3, sf. 544].
Bir biyolog erkek ve dişi çekirgelerin uzunluk ölçümünü (ölçek milimetre) alıyor. Bu iki ölçümlerin ortalaması birbirinden farklı mıdır?
a = [5.20, 4.70, 5.75, 7.50, 6.45, 6.55, 4.70, 4.80, 5.95, \
5.20, 6.35, 6.95, 5.70, 6.20, 5.40, 6.20, 5.85, 6.80, \
5.65, 5.50, 5.65, 5.85, 5.75, 6.35, 14.1, 12.2, 14.0, 14.6, \
5.75, 5.95, 5.90, 7.00, 6.10, 5.80]
b = [8.25, 9.95, 5.90, 7.05, 8.45, 7.55,\
9.80, 10.80, 6.60, 7.55, 8.10, 9.10, \
6.10, 9.30, 8.75, 7.00, 7.80, 8.00, \
9.00, 6.30, 8.35, 8.70, 8.00, 7.50, \
9.50, 8.30, 7.05, 8.30, 7.95, 9.60 ]
a = np.array(a)
b = np.array(b)
ma = np.mean(a); sa = np.std(a,ddof=1)
mb = np.mean(b); sb = np.std(b,ddof=1)
from scipy.stats.distributions import norm
sw = np.sqrt(sa**2/len(a) - sb**2/len(b))
print ((mb-ma) + np.array([-1,1]) * norm.ppf(0.975)*sw)[ 0.53624225 2.09983618]Yüzde 95 güven aralığı 0 değerini içermediği için nüfus ortalamalarının birbirinden farklı olduğu sonucuna varıyoruz.
Verinin Yüzde Kaçı, Ortalama
Verinin yüzde 68’inin hangi aralık olduğu hesabı biraz farklı, ve daha basit. Mesela kafatası ölçümü için
print (np.array([dfetr.mean() - dfetr.std(),
dfetr.mean() + dfetr.std()]).T)Yani ortalam etrafında sağda ve solda tek standart sapmayla belirli bölge, bir Normal dağılımın yüzde 68’ine tekabül eder, ve bir veri Normal şekilde dağılmış ise, o verinin yüzde 68’inin hangi aralıkta olduğu bu şekilde hesaplanabilir.
[[137.80833099 149.80612685]]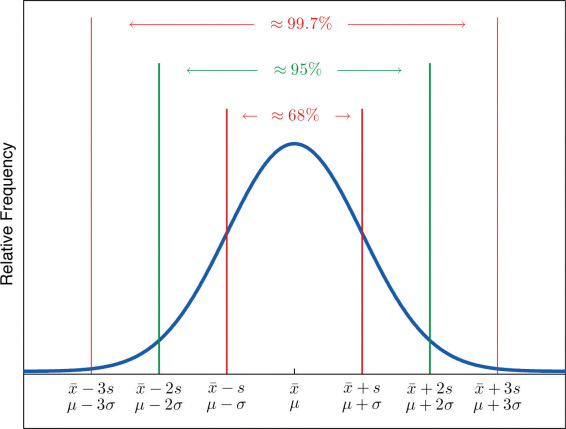
Yüzde 95 hesabı için sağda ve solda iki standart sapmaya bakmak gerekir,
print (np.array([dfetr.mean() - 2*dfetr.std(),
dfetr.mean() + 2*dfetr.std()]).T)[[131.80943306 155.80502478]]Peki yüzde 68, yüzde 95, gibi değerlerin standart sapma ile bağlantısının nereden biliyoruz? Düşünelim, her normal dağılım standart normal dağılıma indirgenebilir, ve standart normal dağılım \(N(0,1)\)’dir, yani ortalaması 0 standart sapması 1. O zaman bu dağılımın, sıfır etrafında -1 ve +1 sınırları içindeki alan nedir hesabı basit kumulatif yoğunluk ile yapılabilir,
from scipy.stats.distributions import norm
print (norm.cdf(1)-norm.cdf(-1)) # tek standart sapma
print (norm.cdf(2)-norm.cdf(-2)) # iki standart sapma0.6826894921370859
0.9544997361036416Her dağılımın tamamının alanı bilindiği gibi 1, bu sebeple üstteki rakamlar bir yüzde olarak algılanabilir.
Bayes Usulü Güven Aralığı (Confidence Intervals)
Bayes ile bu hesabı yapmak için bir dağılımı baz almak lazım. Eğer sonuç olarak bir tek sayı değil, bir dağılım elde edersek bu dağılım üzerinde güvenlik hesaplarını yaparız. Mesela sonuç, sonsal dağılım (posterior) bir Gaussian dağılım ise, bu dağılımın yüzde 95 ağırlığının nerede olduğu, ve nasıl hesaplandığı bellidir.
Bayes Teorisi
\[ P(A \mid B) = \frac{P(B \mid A)P(A)}{P(B)} \]
Veri analizi bağlamında diyelim ki deneyler yaparak tahmini olarak hesaplamak (estimate) istediğimiz bir parametre var, bu bir protonun kütlesi ya da bir ameliyat sonrası hayatta kalma oranı olabilir. Bu durumlarda iki ayrı “olaydan” bahsetmemiz gerekir, B olayı spesifik bazı ölçümlerin elde edilmesi “olayıdır”, mesela ölçüm üç sayıdan oluşuyorsa, biz bir ölçümde spesifik olarak \(\{0.2,4,5.4\}\) değerlerini elde etmişiz. İkinci olay bilmediğimiz parametrenin belli bir değere sahip olması olacak. O zaman Bayes Teorisinin şu şekilde tekrar yazabiliriz,
\[ P(parametre \mid veri ) \propto P(veri \mid parametre)P(parametre) \]
\(\propto\) işareti orantılı olmak (proportional to) anlamına geliyor. Böleni attık çünkü o bir sabit (tamamen veriye bağlı, tahmini hesaplamak istediğimiz parametreye bağlı değil). Tabii bu durumda sol ve sağ taraf birbirine eşit olmaz, o yüzden eşitlik yerine orantılı olmak işaretini kullandık. Bu çerçevede “belli bir sayısal sabit çerçevesinde birbirine eşit (equal within a numeric constant)” gibi cümleler de görülebilir.
Örnek
Diyelim ki bir bozuk para ile 10 kere yazı-tura attık, ve sonuç altta
T H H H H T T H H H
Bu veriye bakarak paranın hileli olup olmadığını anlamaya çalışacağız. Bayes ifadesini bu veriye göre yazalım,
\[ P(p | \{ \textrm{T H H H H T T H H H} \} \propto P(\{ \textrm{T H H H H T T H H H} | p) P(p) \} \]
\(P(p)\) ifadesi ne anlama gelir? Aslında bu ifadeyi \(P([Dagilim] = p)\) olarak görmek daha iyi, artık \(p\) parametresini bir dağılımdan gelen bir özgün değer olarak gördüğümüze göre, o dağılımın belli bir \(p\)’ye eşit olduğu zamanı modelliyoruz burada. Her halükarda \(P(p)\) dağılımını, yani onsel (prior) olasılığı bilmiyoruz, hesaptan önce her değerin mümkün olduğunu biliyoruz, o zaman bu onsel dağılımı düz (flat) olarak alırız, yani \(P(p) = 1\).
\(P( \{\textrm{T H H H H T T H H H} \} | p)\) ifadesi göz korkutucu olabilir, ama buradaki her öğenin bağımsız özdeşçe dağılmış (independent identically distributed) olduğunu görürsek, ama bu ifadeyi ayrı ayrı \(P( \textrm{T} | p)\) ve \(P( \textrm{H} | p)\) çarpımları olarak görebiliriz. \(P( \textrm{T} | p) = p\) ve \(P( \textrm{H} | p)=1-p\) olduğunu biliyoruz. O zaman
\[ P(p | \{ \textrm{7 Tura, 3 Yazı} \} \propto p^7(1-p)^3 \]
Grafiklersek,
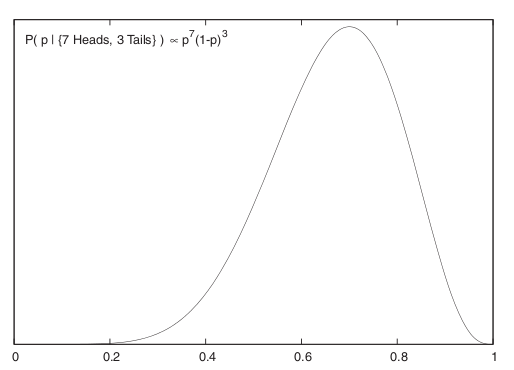
Böylece \(p\) için bir sonsal dağılım elde ettik. Artık bu dağılımın yüzde 95 ağırlığının nerede olduğunu rahatça görebiliriz / hesaplayabiliriz. Dağılımın tepe noktasının \(p=0.7\) civarında olduğu görülüyor. Bir dağılımla daha fazlasını yapmak ta mümkün, mesela bu fonksiyonu \(p\)’ye bağlı başka bir fonksiyona karşı entegre etmek mümkün, mesela beklentiyi bu şekilde hesaplayabiliriz.
Önsel dağılımın her noktaya eşit ağırlık veren birörnek (uniform) seçilmiş olması, yani problemi çözmeye sıfır bilgiden başlamış olmamız, yöntemin bir zayıflığı olarak görülmemeli. Yöntemin kuvveti elimizdeki bilgiyle başlayıp onu net bir şekilde veri ve olurluk üzerinden sonsal tek dağılıma götürebilmesi. Başlangıç ve sonuç arasındaki bağlantı gayet net. Fazlası da var; ilgilendiğimiz alanı (domain) öğrendikçe, başta hiç bilmediğimiz onsel dağılımı daha net, bilgili bir şekilde seçebiliriz ve bu sonsal dağılımı da daha olması gereken modele daha yaklaştırabilir.
Kaynaklar
[1] Larsen, Introduction to Mathematical Statistics and Its Applications
[2] Runger, Applied Statistics and Probability for Engineers
[3] Dekker, Probability and Statistical Inference