AABB Ağaçları ile Çarpışma Saptamasına Giriş
Bir [oyun] dünyasına hareket eden objeler veya herhangi bir şey eklediğiniz anda, çarpışmaları tespit etmeyi düşünmeye başlarsınız ve bunu verimli bir şekilde yapmak, farklı yaklaşımların farklı koşullar için az ya da çok optimal olmasıyla birlikte ilginç bir geliştirme alanı olmaya devam eder. Bu aslında bir mekansal organizasyon problemidir. Bu nedenle, "çarpışma tespiti, bunun bana ne faydası var?" diye düşünebilseniz de, benzer indeksleme yaklaşımlarının oyunları içermeyen benzer soruları yanıtlamada nasıl faydalı olabileceğini görmek zor değildir. Benzer şekilde, örneğin A* algoritması geleneksel olarak bir oyun algoritması olarak düşünülse de, kendimi onu oyun dışı bazı çok ilginç alanlarda kullanırken buldum.
Benim [motorumdaki] objeler arasındaki çarpışmalar söz konusu olduğunda, belirsiz, ancak esasen çok büyük ve çoğunlukla seyrek, üç boyutlu bir alana yayılmış, toplamda milyonlarca parçadan oluşan yüzlerce nesneyi dikkate almam gerekiyor. Bu objelerin her biri arasındaki mükemmel çakışma tespitinin çok maliyetli olacağı bellidir ve bu yüzden çarpışma tespiti tipik olarak iki aşamaya ayrılır:
Kaba hatlı çarpışma saptaması – muhtemel çarpışmaların kısa bir listesini hızla çıkarmaktır. Detaylı çarpışmalar – kaba hatlı adımdan kaynaklanan muhtemel çarpışmaları filtreleyerek gerçek piksel / [nesne] bazında mükemmel çarpışmalara indirgemek için ek detay kullanır. Motorumdaki kaba problemi çözmeye yönelik ilk denemem yaygın bir yöntemdir ve iki kutunun (2D veya 3D) kesişip kesişmediğini belirlemenin, kutuların eksenlere hizalı olmasına dayanan verimli bir yolundan yararlanır – bu nedenle eksenlere hizalı sınırlayıcı kutu (axis aligned bounding box) veya AABB denir. Eğer bu kulağa karmaşık geliyorsa – endişelenmeyin, daha sonra açıklayacağım.
Bunun Internet'te birçok uygulaması ve çeşitli blog yazıları ile eğitimleri mevcuttur ancak hepsini bir araya getiren bir şey bulamadım ve bu nedenle aşağıda, AABB'lere ve kesişimleri hızla belirlemek için bunların bir ağaç yapısında nasıl sıralanacağına dair adım adım bir kılavuz yazdım. Motorumdaki C++ uygulamasının örnek kodu sağlanmıştır ve bu yazının sonunda bunu (sadece AABB ağaç uygulamasını) kendi kodunuzda nasıl kullanabileceğinizi açıklıyorum. Ancak bu yazı daha çok teoriyle ilgilidir ve bunu anladığınızda basit bir uygulamanın oldukça kolay olduğunu göreceksiniz (ancak işleri karmaşıklaştırabilen çok sayıda optimizasyon vardır; bunların bazıları örnek kodumda mevcut, bazıları ise değildir).
Bu kılavuzu basit tutmak amacıyla, 3 boyutlu kutular yerine 2 boyutlu kutular (dikdörtgenler) ile konuşacağım ancak 3. boyutu eklemek için kelimenin tam anlamıyla sadece 3. boyutu eklemeniz yeterlidir. Aşağıda x ve y'nin geçerli olduğu her yerde, x ve y için olan aynı örüntüyü takip ederek z'yi ekleyin. Umarım bu durum örnek kodda açıktır...
AABB'ler Nedir?
AABB'ler göründüklerinden daha basittirler – esasen eksenleri (2D için x,y ve 3D için x,y,z) aynı yönde hızalanan ve uzanan kutulardır. İsimdeki "sınırlayıcı" (bounding) kısmı, çarpışma tespiti için veya bir ağacın parçası olarak kullanıldıklarında genellikle diğer kutuları içermelerinden veya sınırlamalarından kaynaklanır. Aşağıdaki diyagram, iki basit ve uyumlu AABB'yi göstermektedir:
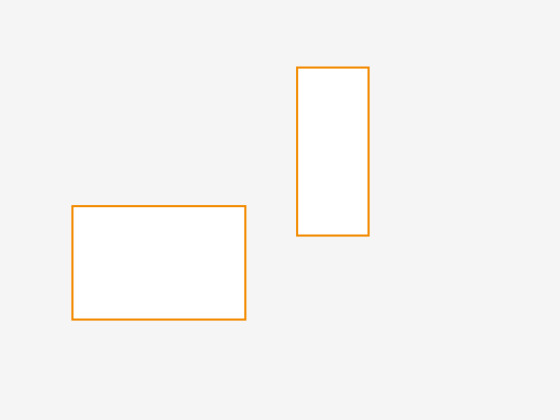
Buna karşılık, aşağıdaki diyagramda gösterilen iki kutu, eksenleri hizalanmadığı için AABB değildir:

Bir AABB'nin temel bir özelliği, kapladığı alanın 2 veya 3 boyutlu uzayda olmasına bakılmaksızın 2 nokta ile tanımlanabilmesidir. 2 boyutlu bir uzayda bu 2 nokta (minx, miny) ve (maxx, maxy)'dir.
Bu, iki AABB'nin kesişip kesişmediğini çok hızlı bir şekilde kontrol etmek için kullanılabilir. Aşağıdaki diyagramdaki iki AABB'yi ele alalım:
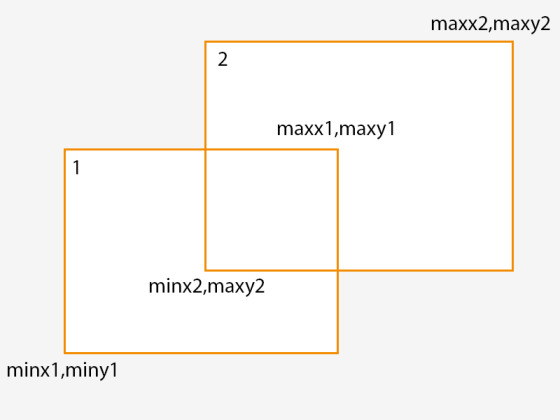
Bu diyagramda, bir çift nokta ile tanımlanan iki AABB'miz var ve aşağıdaki ifadenin sonucu, kesişip kesişmediklerini belirleyebilir:
maxx1 > minx2 && minx1 < maxx2 && maxy1 > miny1 && miny1 < maxy2
Bu ifadeyle ilgili dikkat edilmesi gereken önemli bir nokta, bir dizi 've' (and) işleminden oluşmasıdır, bu da koşullardan biri sağlanmazsa (false olursa) değerlendirmenin hemen duracağı anlamına gelir [yazarın bahsettiği "kısa-devre değerlendirmesi" (short-circuit evaluation), eğer bir dizi VE ifadesi var ise terimlerden biri yanlış değeri verirse geri kalan terimleri hesaplamaya ihtiyaç yoktur çünkü VE zincirinin tamamının doğru sonucunu vermesi için tüm ifadelerin doğru olması gerekir, o zaman ilk yanlışta zincirden çıkılabilir (kısa devre) bu bir hızlandırıcı tekniktir, bir tür optimizasyondur].
Bir oyun motorunda çalıştığım için şanslıyım çünkü oyun dünyamdaki nesneler doğal olarak eksen hizalıdır: [nesneler] esasen 3 boyutlu pikseller veya küçük küplerdir. Ancak ya nesneleriniz doğal olarak hizalı değilse veya kutular dışında şekillerden oluşuyorsa? İşte burada AABB'nin sınırlayıcı kısmı devreye girer, çünkü aşağıdaki diyagramda gösterildiği gibi karmaşık şekli kapsayan bir sınırlayıcı kutu oluşturmanız gerekir:
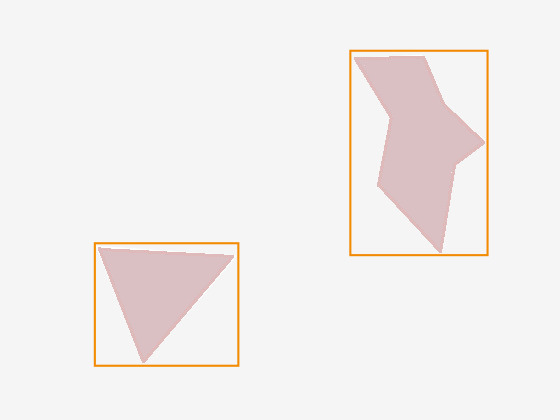
Tabii ki AABB'yi kesişim için test etmek piksel hassasiyetinde çarpışma tespitiyle sonuçlanmayacaktır, ancak AABB kullanmanın birincil amacının sürecin geniş kapsamlı (broad phase) kısmında olduğunu unutmayın. Yukarıdaki diyagramdaki iki AABB'nin kesişmediğini hızlı ve ucuzca belirledikten sonra, iki karmaşık şeklin kesişip kesişmediğini anlamaya çalışmanın hesaplama maliyetinden kendimizi kurtarabiliriz.
AABB Ağacı
Yukarıdaki yaklaşımı kullanarak, dünya uzayınızdaki iki nesne arasındaki çarpışmaları nasıl hızlı ve kolay bir şekilde test edebileceğimizi görebilirsiniz, ancak ya 100 nesneniz varsa? Veya 1000? Bireysel testler ne kadar verimli olursa olsun, 1000 AABB'yi birbirleriyle karşılaştırmak maliyetli ve oldukça israflı bir işlem olacaktır.
İşte burada AABB ağacı devreye girer. Yapılması gereken AABB kesişim testi sayısını en aza indirmek için AABB'lerimizi organize etmemizi ve indekslemek; AABB ağacı bunu dünyayı -tahmin edin ne kullanarak- daha fazla AABB kullanarak, dilimleyerek yapar. Yani AABB ağacı AABB'leri indeksler, bunun kodlamasında yardımcı olarak iç yapısında aynı AABB kavramını kullanır.
Daha önce karşılaşmadıysanız, ağaçlar inanılmaz derecede kullanışlı hiyerarşik veri yapılarıdır ve temel kavramın birçok çeşidi vardır, eğer bu tür şeyler ilginizi çekiyorsa, konuyla ilgili mükemmel, ancak oldukça resmi bir kitap Cormen'in Algoritmaya Giriş (Introduction to Algorithms) kitabıdır ve devam etmeden önce yapı ve terminoloji hakkında temel bilgi edinmeye değer.
Burada sunulan AABB ağacı durumunda kök, dal ve yaprakların çok özel özellikleri vardır:
Dal (Branch) – Dallarımızın her zaman tam olarak iki çocuğu (sol ve sağ olarak bilinir) vardır ve tüm alt öğelerini (descendants) içerecek kadar büyük bir AABB atanır.
Yaprak (Leaf) – Yapraklarımız bir oyun dünyası nesnesiyle ilişkilidir ve bu sayede bir AABB'ye sahiptir. Bir yaprağın AABB'si tamamen ebeveyninin AABB'sinin içine sığmalıdır ve dallarımızın nasıl tanımlandığı nedeniyle bu, her ata (ancestor) AABB'sinin içine sığdığı anlamına gelir.
Kök (Root) – Kökümüz bir dal veya bir yaprak olabilir.
Bunun nasıl çalıştığını göstermenin en iyi yolu, onu adım adım gösteren bir örnektir.
Bir AABB Ağacı Oluşturma
Boş bir dünyamız olduğunu ve dolayısıyla bu noktada ağacımızın boş olduğunu hayal edin. Bu dünyaya ilk nesnemizi ekliyoruz. Ağacımız şu anda boş olduğundan, yeni nesnemize karşılık gelen ve onun AABB'sini paylaşan bir yaprak düğümü oluştururuz ve bu yaprağı kök olarak atıyoruz:

Şimdi dünyamıza ikinci bir nesne ekliyoruz, ilk düğümümüzle kesişmiyor ve ağacımızda ilginç bir şey oluyor:
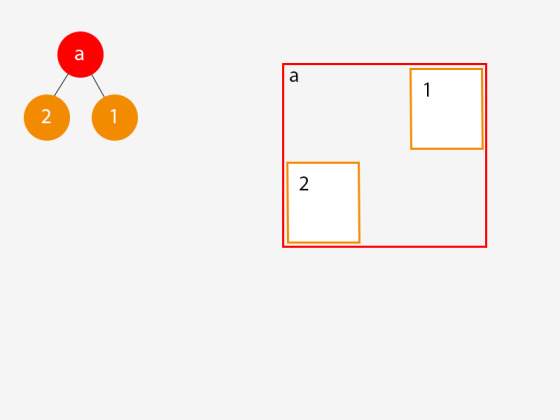
İkinci nesneyi oyun dünyasına eklediğimizde bir dizi şey meydana geldi:
Ağacımız için bir dal düğümü oluşturduk ve ona hem nesne (1)'i hem de nesne (2)'yi içerecek kadar büyük bir AABB atadık.
Nesne (2) için yeni bir yaprak düğümü oluşturduk ve onu yeni dal düğümümüze bağladık.
Nesne (1) için orijinal yaprak düğümümüzü aldık ve onu yeni dal düğümümüze bağladık.
Yeni dal düğümünü ağacın kökü yaptık.
Tamam. Oyun dünyasına başka bir nesne ekleyelim ve bu sefer mevcut bir nesneyle kesişsin:
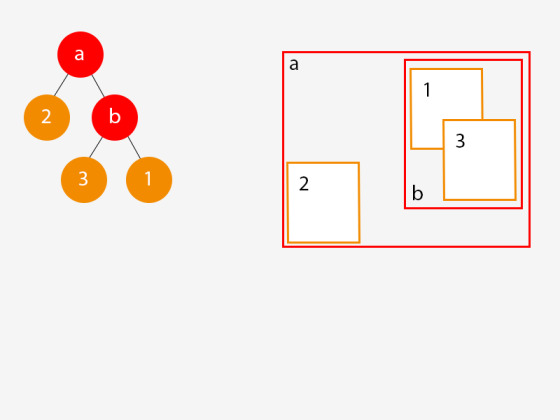
Yine bu nesneyi eklediğimizde ağacımızda bazı ilginç şeyler oldu:
Yeni bir dal düğümü (b) oluşturduk ve ona nesne (1) ve (3)'ü kapsayan bir AABB atadık.
Nesne (3) için yeni bir yaprak düğümü oluşturduk ve onu dal (b)'ye atadık.
Yaprak düğüm (1)'i dal düğüm (b)'nin bir çocuğu olacak şekilde taşıdık ve bu yeni dal düğümünü (b) dal düğüm (a)'ya bağladık.
Bu ince ama önemli bir nokta: dal düğüm (a)'ya atanan AABB'yi, yeni yaprak düğümünü hesaba katacak şekilde ayarladık. Eğer bunu yapmasaydık, dal düğüm a'ya atanan AABB artık alt öğelerinin AABB'lerini içerecek kadar büyük olmazdı.
Esasen, her yeni oyun dünyası nesnesi eklediğimizde, ağacı daha önce tanımladığım dal ve kök düğümleri kuralları hala geçerli olacak şekilde manipüle ederiz. Durum böyle olduğuna göre, ağaca yeni bir oyun dünyası nesnesi eklemek için genel bir süreci tanımlayabiliriz:
Nesne için bir yaprak düğümü oluşturun ve ona ilişkili nesneye dayalı bir AABB atayın.
Ağaçta, yeni yaprağı kardeş yapmak için en iyi mevcut düğümü (yaprak veya dal) bulun.
Bulunan düğüm ve yeni yaprak için yeni bir dal düğümü oluşturun ve ona her iki düğümü de içeren bir AABB atayın (esas olarak bulunan düğümün ve yeni yaprağın AABB'lerini birleştirin).
Yeni yaprağı yeni dal düğümüne bağlayın.
Mevcut düğümü ağaçtan kaldırın ve yeni dal düğümüne bağlayın.
Yeni dal düğümünü, mevcut düğümün önceki ebeveyn düğümünün bir çocuğu olarak bağlayın.
Ağaçta yukarı doğru geri giderek, tüm atalarımızın AABB'lerini, hala tüm alt öğelerinin AABB'lerini içerdiklerinden emin olmak için ayarlayın.
Yukarıdaki 2. adım şu soruyu akla getiriyor: Yeni yaprağı kardeş yapmak için ağaçtaki en iyi yaprağı nasıl bulursunuz? Esasen bu, ağaçta aşağı inip geçtiğiniz her dalın soluna veya sağına bağlanmanın olası maliyetini değerlendirmeyi içerir. Ne kadar iyi bir karar verirseniz, ağaç o kadar dengeli olur ve sonraki sorgular o kadar ucuz olur.
Burada kullanılan yaygın bir sezgisel yöntem (heuristic), yeni yaprağın AABB'sinin eklenmesi için ayarlanmış olan sol ve sağ düğümlerin yüzey alanına bir maliyet atamak ve kendinizi bir yaprakta bulana kadar en ucuz düğüm yönünde inmektir.
AABB Ağacını Sorgulama
İşte tüm ağır çalışmamızın karşılığını aldığımız yer – sorgulama artık çok basit ve çok hızlı olacak. Belirli bir AABB nesnesi için tüm olası çarpışmaları bulmak istiyorsak, ağacın kökünden başlayarak yapmamız gereken tek şey şudur:
Mevcut düğümün test nesnesinin AABB'si ile kesişip kesişmediğini kontrol edin.
Eğer kesişiyorsa ve bir yaprak düğümse, bu bir çarpışmadır ve bu yüzden onu çarpışma listesine ekleyin.
Eğer kesişiyorsa ve bir dal düğümse, o zaman sola ve sağa inin ve bu işlemi özyinelemeli (recursive) olarak tekrarlayın.
Yukarıdakilerin sonunda listeniz, test nesneniz için tüm olası çarpışmaları içerecektir ve test AABB ağacıyla kesişemeyecek hiçbir yola (ve dolayısıyla sonraki tüm çocuklara) inmediğimiz için yapmamız gereken AABB kesişim kontrolü sayısını en aza indirmiş olacağız.
Uygulamada, büyük ağaçlarda maliyetli olabileceği (ve başarısız olabileceği) için aslında özyinelemeli bir yaklaşım kullanmamak en iyisidir. Bunun yerine, aşağıdaki gibi daha fazla araştırılacak düğümlerin bir yığınını / listesini tutun:
Kök düğümü bir yığına (stack) itin (C++'da
std::stackkullanıyorum)Yığın boş olmadığı sürece:
Yığından bir düğüm çıkarın (pop).
Düğümün test AABB nesnesiyle kesişip kesişmediğini kontrol edin.
Eğer kesişiyorsa, ya:
Eğer bir yaprak düğümse, bu bir çarpışma eşleşmesidir. Yaprak düğümü (veya referans verdiği nesneyi) çarpışma listesine ekleyin.
Eğer bir dal düğümse, çocukları (sol ve sağ düğümleri) yığına itin (push).
Ağaçları özyinelemesiz olarak nasıl dolaşacağınızı anlamak çok faydalı olabilir.
AABB Ağacını Güncelleme
Çarpışma tespiti içeren çoğu (ama hepsi değil) senaryoda, dünyadaki nesnelerin en azından bir kısmı hareket etmektedir. Nesneler hareket ettikçe, bu durum ağacın güncellenmesini gerektirir ve bu, dünya nesnesine karşılık gelen yaprağın kaldırılıp yeniden eklenmesiyle gerçekleştirilir.
Bu pahalı bir işlem olabilir ve dünya nesnelerinizin hareketini bir hız vektörü kullanarak ifade ederseniz ve bunu ağaca eklediğiniz AABB'leri "genişletmek" (fatten) için kullanırsanız, bunu yapmanız gereken sayıyı en aza indirebilirsiniz. Örneğin, aşağıdaki diyagramdaki nesneyi ele alın, (1,0) (x,y) hızına sahiptir ve sınırlayıcı AABB'si buna göre genişletilmiştir:

AABB'leri ne kadar genişleteceğiniz; güncelleme maliyeti, öngörülebilirlik ve geniş aralık doğruluğu arasında bir denge meselesidir ve en iyi performansı elde etmek için denemeler yapmanız gerekebilir.
Son olarak, ağaçlar güncellendikçe dengesiz hale gelmeleri mümkündür; bazı sorgular uygunsuz bir şekilde diğerlerinden çok daha fazla düğümün dolaşılmasını gerektirebilir. Bunu çözmek için bir teknik, her düğümün yüksekliğine (alttan derinlik) dayalı rotasyonlar kullanarak ağacı yeniden dengelemektir. Bir diğeri ise, çocuk düğümlerin ebeveyn düğümlerinin AABB'sini ne kadar eşit böldüğüne göre ağacı dengelemektir. Bu, başlangıç seviyesi bir rehberin kapsamının biraz dışındadır ve henüz örnek kodda kendim uygulamadım – ancak bir noktada buna geri dönebilirim.
Örnek Kod
Son olarak, bu blog yazısıyla birlikte gelen örnek kod bulunmaktadır ve bunu oyun motorumda bulabilirsiniz. Motorun kendisinden oldukça bağımsızdır ve çok fazla sorun yaşamadan kendi kodunuzda kullanabilmelisiniz. Anahtar dosyalar şunlardır:
- AABB.h
- AABBTree.h
- AABBTree.cpp
- IAABB.h
- AABB.py (biz ekledik, Python tercümesi, Google Gemini 2.5 ile yapıldı)
Ağacı kullanmak için üstteki dört C++ dosyasını projenize eklemeniz ve AABBTree sınıfının bir örneğini oluşturmanız gerekecektir – yapıcısı (constructor) çok basittir ve başlangıç boyutunu (önceden ayrılacak ağaç düğümü sayısı) alır. Ağaca eklemek istediğiniz herhangi bir nesnenin, istendiğinde AABB yapısını döndürmesi gereken IAABB arayüzünü (interface) uygulaması gerekir. Bu nesneleri sırasıyla insertObject, updateObject ve removeObject yöntemleriyle ekleyebilir, güncelleyebilir ve kaldırabilirsiniz ve queryOverlaps yöntemiyle çakışmaları sorgulayabilirsiniz.
Yukarı