GPS, Kullanıcı Yerini Bulmak, GPS Uydularına Olan Açı, Uzaklık
Küresel Konumlama Sistemi (Global Positioning System -GPS-) ile dünyada nerede olduğumuzu kolay bir şekilde bulabiliyoruz. GPS'in temelinde eldeki bir alıcının dünya etrafında sürekli dönen uydulara olan mesafesini ölçerek bunlara göre bir konumlama yapması yatıyor. Eldeki alıcı, ki artık ucuz bir akıllı telefon bile olabiliyor, önce Almanak denen bir bilgiyi (eğer o anda elde yoksa) uydudan alıyor. Bu bilgi tüm GPS uydularının kesin yerlerini alıcıya söyler. Ardından uydu ve alıcı arasında sinyallerin alınıp verilmesindeki zaman farkına bakılarak olabildiğince detaylı bir mesafe bilgisi alınır. Eğer en az 4 tane uyduya olan mesafe bu şekilde alınabiliyorsa bir üçgenleme yapılarak alıcının yeryüzündeki yeri saptanabilir. Uydular her biri yeterince büyük bir bölgeye servis edebilsin diye çok uzaktaki bir yörüngededirler, dünyaya ortalama mesafeleri 20,000 kilometre (evet, yirmi bin), kıyasla ISS uzay istasyonu yaklaşık 200 km. mesafede.
Bu yazıda mesafeleri kullanıp nerede olduğumuz konusuna girmeden eğer nerede olduğumuz biliniyor olsa uyduya olan yatay açı / azimut (azimuth) ve yüksekliği (elevation) nasıl buluruz konusunu işleyeceğiz.
Azimut nedir? Yeryüzünde duruyoruz, yüzümüzü kuzeye dönelim, bu referans duruşu. Eğer mesela azimut 320 derece ise, doğuya doğru o kadar döneriz (ya da batıya 360-320 kadar dönebiliriz), ve başımızı yukarı doğru yükseklik açısı kadar kaldırırız, mesela 60 derece yukarı doğru, ki 90 derece tam dik yukarı bakıyoruz demektir. Aşağı yukarı alttaki resimdeki gibi bir durum olur,
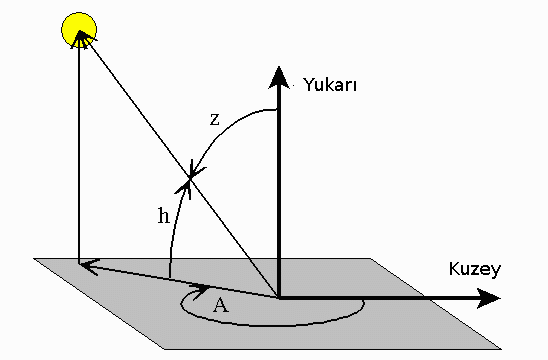
Üstteki türden bir gösterim kullanıcı merkezlidir. GPS uyduları, hatta kullanıcının yerini dünyayı merkez alan, daha net şekilde belirtmek gerekirse dünyanın merkezini merkez alan (orası orijin sayılıyor, (0,0,0) noktası) sisteminde almak daha kullanışlı oluyor.
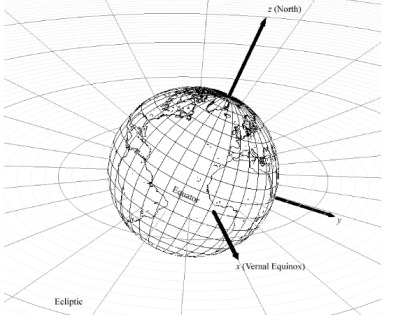
Bu sisteme ECI sistemi, ya da ECEF kordinatları deniyor. Tabii mesela kilometre bağlamında mesela (1,1,1) noktası anlamsız olabilir, dünyanın "içinde", yerkabuğunun altında bir nokta olacaktır, fakat dünya yüzeyi, ve yüzeyden daha üstteki uydular için anlamlı ve kullanışlı bir sistem. Daha önemlisi bu sistem Kartezyen geometrisi kullanmamıza izin verecek, ve daha ileride göreceğimiz gibi uzaklık hesaplarında faydalı olacak. ECI ve alıcı bazlı kordinat sistemlerini aynı resimde görelim,
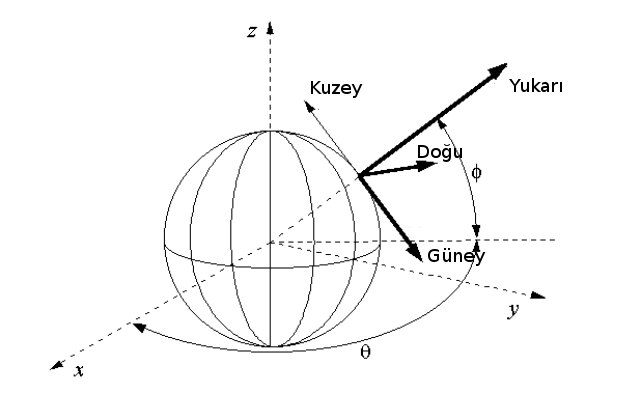
Hesabın detayları [3]'te bulunabilir. Dünyanın duruşunun hesabı için yıldız günü (sidereal day) kavramı gerekli. Bilinen gün hesabı güneşin aynı boylamdan iki geçişi arasındaki zamandır. Öğlen 12'de güneş yukarıdadır, güneşin tekrar aynı noktada olduğu zaman bir gün geçmiş demektir. Fakat astronomi hesapları için etrafında döndüğümüz güneş değil, daha uzaktaki bir noktayı merkez almak gerekebiliyor, bu daha uzaktaki noktanın aynı boylamın üzerinden iki geçişi arasındaki zaman bir yıldız günüdür. Normal gün ile yıldız günü arasında 4 dakikalık bir fark var. Yıldız günü ve ayrıca tek reel sayı bazlı tarih kullanabilmek için için Jülyen Tarihi kullanılır, bu tarih bir referans başlangıç anından mevcut ana olan gün sayısıdır. Altta bazı ölçümler aldığımız zamanı milisaniye olarak kaydettik, onun Jülyen çevrimi alttaki gibi hesaplanıyor,
import orbital
from datetime import datetime
millis = 1493036068479
dt = datetime.fromtimestamp(millis/1000.0)
dtj = orbital.jdays(datetime.fromtimestamp(millis/1000.0))
print dtj
2457868.09339
Azimut, yükseklik hesapları ölçüm aldığımız an için [1]'den uyduların nerede olduğunu bir dosyaya kaydettik. GPS uydularının PRN kodları vardır, örnek seçilen PRN 11,18,16,24,31 uydularının enlem / boylam pozisyonları altta,
import pandas as pd
df = pd.read_csv('Waas_Sv_Status.txt',sep='\s*',index_col=0)
sats = [11,18,16,24,31]
df = df.ix[sats]
print df[['Lat','Long']]
Lat Long
PRN
11 30.518234 -164.259351
18 1.027207 -57.092297
16 -55.533692 -122.123140
24 45.299193 17.625305
31 13.344068 -102.581100
Ölçüm alınan yerin kordinatları altta lat,lon içinde. Şimdi bu
noktadan bakılacak olsa (Berlin'deyiz) uyduların hangi azimut, yükseklikte
olacağının hesabını yapalım,
lon = 13.442383333333332
lat = 52.483086666666665
alt = 0
sat_alt = 20*1000*1000
print df.apply(lambda x: orbital.get_observer_look(x.Long, \
x.Lat, sat_alt, dt, lon, lat, alt),axis=1)
PRN
11 (358.005492414, -6.99245765159, 20007166.964)
18 (254.95693367, 12.52250143, 20004991.9173)
16 (245.378821316, -64.1703023622, 20012088.4789)
24 (157.451172143, 82.3085240779, 20000057.3405)
31 (298.723320912, -4.42938085218, 20006877.4437)
dtype: object
[2]'den tüm uyduların o anda dünya üzerinde nerede olduğuna baktık,
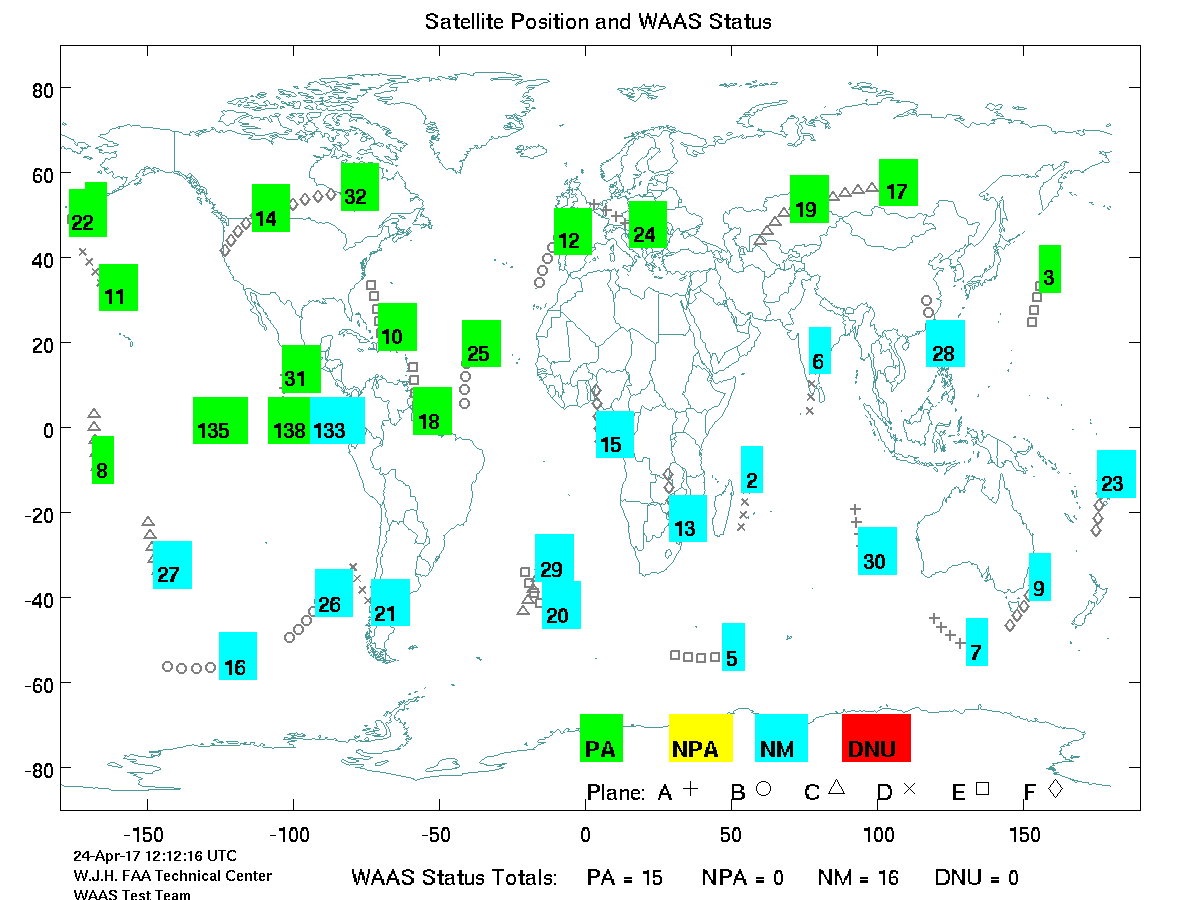
Peki bu hesapları mesela cep telefonunun aldığı azimut, yükseklik ile karşılaştırsak ne görürüz?
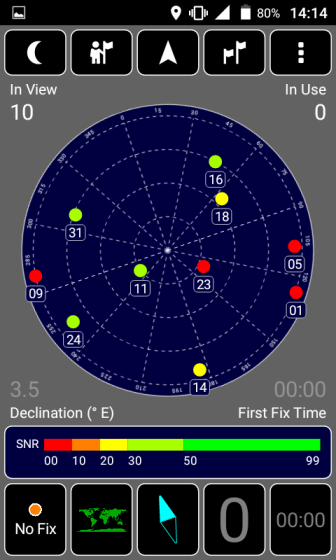
Telefonun raporladığı rakamlar uydu ve alıcı pozisyonuna göre değil, antene ve sinyale göre hesaplanıyor, GPS kitlemesi yapılmadan da bu değerleri bir GPS programında [7] görebiliyoruz. 11,31,24 fena durmuyor, fakat 18 tam ters yönde çıkmış. Telefondaki ölçümlere tam güvenilir diyemeyiz. Zihin egzersizi: acaba elde yeteri kadar azimut, yükseklik ölçümü olsa ve uydu pozisyonu ile birleştirince üstteki hesapta geriye doğru giderek bir alıcı pozisyonu elde edilebilir mi? İstatistiki bir yaklaşım belki bunu yapabilir. Ödev olsun!
Tüm kodlar
from datetime import datetime
import numpy as np, math
F = 1 / 298.257223563 # Dunya duzlestirme WGS-84
MFACTOR = 7.292115E-5
EPS_COS = 1.5e-12
F = 1 / 298.257223563 # Dunya duzlestirme WGS-84
A = 6378.137 # WGS84 ekvotarsal cap
a = 6378137.0 # tekrar
# yari minor eksen uzunlugu (m)
b = 6356752.3142
# elipsoid duzluk (birimsiz)
f = (a - b) / a
# eksentriklik (birimsiz)
e = np.sqrt(f * (2 - f))
def jdays2000(utc_time):
return _days(utc_time - datetime(2000, 1, 1, 12, 0))
def jdays(utc_time):
return jdays2000(utc_time) + 2451545
def _fdays(dt):
return (dt.days + (dt.seconds + \
dt.microseconds / (1000000.0)) / (24 * 3600.0))
_vdays = np.vectorize(_fdays)
def _days(dt):
return _fdays(dt)
def gmst(utc_time):
ut1 = jdays2000(utc_time) / 36525.0
theta = 67310.54841 + ut1 * (876600 * 3600 + 8640184.812866 + ut1 *
(0.093104 - ut1 * 6.2 * 10e-6))
return np.deg2rad(theta / 240.0) % (2 * np.pi)
def observer_position(time, lon, lat, alt):
lon = np.deg2rad(lon)
lat = np.deg2rad(lat)
theta = (gmst(time) + lon) % (2 * np.pi)
c = 1 / np.sqrt(1 + F * (F - 2) * np.sin(lat)**2)
sq = c * (1 - F)**2
achcp = (A * c + alt) * np.cos(lat)
x = achcp * np.cos(theta) # kilometers
y = achcp * np.sin(theta)
z = (A * sq + alt) * np.sin(lat)
vx = -MFACTOR*y # kilometers/second
vy = MFACTOR*x
vz = 0
return (x, y, z), (vx, vy, vz)
def get_observer_look(sat_lon, sat_lat, sat_alt, utc_time, lon, lat, alt):
(pos_x, pos_y, pos_z), (vel_x, vel_y, vel_z) = \
observer_position(utc_time, sat_lon, sat_lat, sat_alt)
(opos_x, opos_y, opos_z), (ovel_x, ovel_y, ovel_z) = \
observer_position(utc_time, lon, lat, alt)
lon = np.deg2rad(lon)
lat = np.deg2rad(lat)
theta = (gmst(utc_time) + lon) % (2 * np.pi)
rx = pos_x - opos_x
ry = pos_y - opos_y
rz = pos_z - opos_z
sin_lat = np.sin(lat)
cos_lat = np.cos(lat)
sin_theta = np.sin(theta)
cos_theta = np.cos(theta)
top_s = sin_lat * cos_theta * rx + \
sin_lat * sin_theta * ry - cos_lat * rz
top_e = -sin_theta * rx + cos_theta * ry
top_z = cos_lat * cos_theta * rx + \
cos_lat * sin_theta * ry + sin_lat * rz
r = np.sqrt(top_s**2+top_e**2+top_z**2)
az_ = np.arctan(-top_e / top_s)
az_ = np.where(top_s > 0, az_ + np.pi, az_)
az_ = np.where(az_ < 0, az_ + 2 * np.pi, az_)
rg_ = np.sqrt(rx * rx + ry * ry + rz * rz)
el_ = np.arcsin(top_z / rg_)
return np.rad2deg(az_), np.rad2deg(el_), r
def ecef2lla(ecef, tolerance=1e-9):
x = ecef[0]
y = ecef[1]
z = ecef[2]
lon = math.atan2(y, x)
alt = 0
N = a
p = np.sqrt(x**2 + y**2)
lat = 0
previousLat = 90
while abs(lat - previousLat) >= tolerance:
previousLat = lat
sinLat = z / (N * (1 - e**2) + alt)
lat = math.atan((z + e**2 * N * sinLat) / p)
N = a / np.sqrt(1 - (e * sinLat)**2)
alt = p / math.cos(lat) - N
return (np.rad2deg(lat), np.rad2deg(lon), alt)
Uzaklıktan Kullanıcı Pozisyonunu Bulmak
Aynı zamanda bir GPS alıcısı olan akıllı cep telefonları GPS uydularına olan mesafeyi hesaplayabilir. Bunu uydudan gönderilen sinyallerin erişim süresini hesaplayarak yaparlar. Uydulardan gelen her sinyal içinde o sinyalin gönderilme anı vardır, alıcı bu zamana bakar, ve kendi elindeki saate bakar ve aradaki farkı sinyalin hızı ile çarparak mesafeyi bulur. Birden fazla yeri bilinen uyduya olan mesafelerin kesişme noktası alıcının olduğu yerdir.
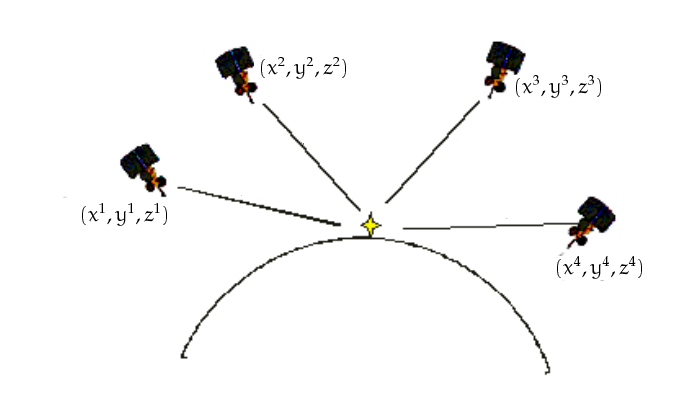
Yanlız bu hesap yapılırken iki potansiyel problem ortaya çıkar.
Birinci problem alıcıdaki saat yanlılık problemi (clock bias). GPS sinyali yerine ses dalgası temelli bir örnek üzerinde bu kavramı anlatalım: Denizcilikte sis sireni (foghorn) denen bir şey var, sisli durumlarda gemicileri yakında tehlikeli kayalar hakkında uyarmak için kullanılır. Şimdi diyelim ki sis sirenini yerimizi bulmak için kullanacağız. Yine basitleştirme amaçlı olarak tek boyutlu bir dünya düşünelim, bir çizgi üzerindeyiz, bu çizgide ya sola ya da sağa gidebiliyoruz, sis sireni ise çizginin sıfır noktasında.
Sis sireninin her gün öğlen 12:00'de çalındığını biliyoruz. Diyelim ki saat 12:00:10 (yani 10 saniye sonra) sireni duyduk. Üstteki çizgide neredeyiz? Ses hızı 330 metre / saniye, o zaman 10 saniye sonra 3.3 kilometre uzaktayız.
Fakat bu hesap eğer saatimiz mükemmel bir şekilde siren saati ile senkronize ise geçerli. Uzaktan bu senkronizasyon var mı yok mu bilemiyoruz, çünkü sireni duyduğumuzda saate baktık acaba önceden 5 saniye geri miydik de 15 saniye sonra gelen sireni acaba 12:00:10'da gördük? Ya da senkronizasyon haricinde belki saatimiz daha yavaş, ya da daha hızlı işliyor, ses havada seyahat ederken bu hızlanma / yavaşlama ölçüme etki etti?
Bu problemden kurtulmak için elimizdeki saatin yanlılığını denklemlerde direk kullanarak onu da hesaplamak bir çözüm olabilir. Yanlılığı modelleyebiliyoruz çünkü sis sirenleri birbirleri ile mükemmel şekilde senkronize (GPS uyduları için de bu böyle, uydularda birbirleri ile senkronize atomik saatler var), ve bizim saatimizde yanlılık varsa bu yanlılık her iki siren için aynı. Yani yanlışlık olması önemli değil, yanlışlık tutarlı ise ondan kurtulabiliriz!
Yanlılık ikinci bir bilinmeyen tabii, o zaman ikinci bir ölçüm lazım. Diyelim ki birinci sirenden 990 m. sağda olan ikinci bir sirenden saat 12:00:09'da bir sinyal aldık.
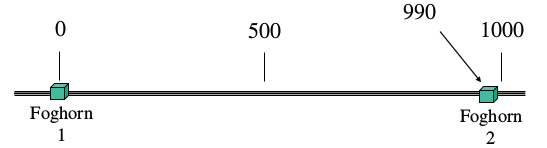
Şimdi nerede olduğumuzu bulabilir miyiz? Uzaklık, daha doğrusu içinde yanlılık ta olduğu için, "sözde uzaklık (pseudorange)" şöyle modellenir,
$$ R_1' = v_{ses} (\Delta t_1 + \tau ) = x + v_{ses}\tau = 3300 $$
$$ R_2' = v_{ses} (\Delta t_2 + \tau ) = 990 - x + \tau = 2970$$
ki $\Delta t_1, \Delta t_2$ geçen zaman, $\tau$ yanlılık, $v_{ses}$ ses hızı. Tekrar düzenlersek,
$$ x + v_{ses} \tau = 3300$$
$$ x - v_{ses} \tau = -1980 $$
Çözersek,
$$ \tau = 8 \textrm{ saniye} \quad x = 660 \textrm{ metre}$$
Yanlılık hesabı böyle. Şimdi ikinci probleme gelelim. Bu problem kesişme hesabı sırasında ortaya çıkıyor. Yanlılık doğru modellense bile diğer pek çok sebepten dolayı uzaklık hesabında eksikler olabilir. O zaman mükemmel kesişme yerine alttaki gibi durum ortaya çıkabilir,
- uydu uzaklığı normalden kısa, 2. ve 3. uzun gelmiş. Acaba bu uzaklıkların gürültülü bir ortamda olsak bile kesiştiği yeri yaklaşık bir şekilde bulamaz mıyız? Hatta sistemi öyle kuralım ki ne kadar çok uydu ölçümü eklersek ölçüm o kadar ilerlesin, yani bir tür istatistiksel en az kareler (least squares) çözümü arıyoruz.
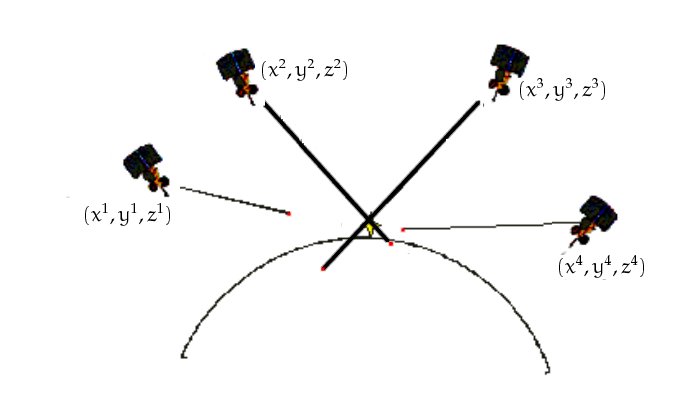
Fakat yine bir problem var, alıcı $x,y,z$ pozisyonu ve uydu $i$ arasındaki sözde mesafe, $P^i$ diyelim, gayrı-lineer bir hesap.
$$ P^i = \sqrt{ \big( (x^i-x)^2 + (y^i-y)^2 + (z^i-z)^2 \big) } + \tau $$
Hesapta kareler, onların toplamı, karekök işlemi var. Üstteki denklemi, ve bu denklemi kullanacağımız denklem sistemini bir şekilde lineerleştirmemiz lazım.
Her sözde uzaklık ölçümünü üstteki model artı gürültü olarak gösterelim,
$$ P_{\textrm{gözlem}} = p_{model} + \textrm{gürültü} $$
$$ = P(x,y,z,\tau) + v $$
Şimdi model üzerinde çok boyutlu Taylor açılımı uygulayalım,
$$ P(x,y,z,\tau) = P(x_0,y_0,z_0,\tau_0) + (x-x_0)\frac{\partial P}{\partial x} + (y-y_0)\frac{\partial P}{\partial y} + (z-z_0)\frac{\partial P}{\partial z} + (\tau-\tau_0)\frac{\partial P}{\partial \tau} + ... $$
Bu açılımda noktalı yerlerde daha yüksek üstelli terimler var, onları atalım, geri kalanlar lineer terimler, ve atılan terimler sebebiyle açılım yaklaşıksal olacak doğal olarak. Taylor açılımını $x_0,y_0,z_0,\tau_0$ noktası "etrafında" yaptık, şimdi $ P(x_0,y_0,z_0,\tau_0)$'e $P_{hesap}$ diyelim, bunun sebebini birazdan göreceğiz, ve tüm denklem şu hale gelir,
$$ = P_{hesap} + \frac{\partial P}{\partial x} \Delta x + \frac{\partial P}{\partial y} \Delta y + \frac{\partial P}{\partial z} \Delta z + \frac{\partial P}{\partial \tau} \Delta \tau $$
Şimdi
$$ \Delta P \equiv P_{\textrm{gözlem}} - P_{hesap} $$
diyelim, ve
$$ = \frac{\partial P}{\partial x} \Delta x + \frac{\partial P}{\partial y} \Delta y + \frac{\partial P}{\partial z} \Delta z + \frac{\partial P}{\partial \tau} \Delta \tau + v $$
Matris formunda yazarsak,
$$ \Delta P = \left[\begin{array}{cccc} \dfrac{\partial P}{\partial x} \Delta x & \dfrac{\partial P}{\partial y} \Delta y & \dfrac{\partial P}{\partial z} \Delta z & \dfrac{\partial P}{\partial \tau} \Delta \tau \end{array}\right] \left[\begin{array}{c} \Delta x \\ \Delta y \\ \Delta z \\ \Delta \tau \end{array}\right] + v $$
Üstteki tek bir ölçüm için. Her uydudan gelen ölçüm matriste yeni bir satır oluşturur, $m$ tane ölçüm için,
$$ \begin{bmatrix} \Delta P^1 \\[1ex] \Delta P^2 \\[1ex] \Delta P^3 \\[1ex] \vdots \\[1ex] \Delta P^m \end{bmatrix} = \begin{bmatrix} \dfrac{\partial P^1}{\partial x} & \dfrac{\partial P^1}{\partial y} & \dfrac{\partial P^1}{\partial z} & \dfrac{\partial P^1}{\partial \tau} \\[2ex] \dfrac{\partial P^2}{\partial x} & \dfrac{\partial P^2}{\partial y} & \dfrac{\partial P^2}{\partial z} & \dfrac{\partial P^2}{\partial \tau} \\[2ex] \dfrac{\partial P^3}{\partial x} & \dfrac{\partial P^3}{\partial y} & \dfrac{\partial P^3}{\partial z} & \dfrac{\partial P^3}{\partial \tau} \\[2ex] \vdots & \vdots & \vdots & \vdots \\[2ex] \dfrac{\partial P^m}{\partial x} & \dfrac{\partial P^m}{\partial y} & \dfrac{\partial P^m}{\partial z} & \dfrac{\partial P^m}{\partial \tau} \end{bmatrix} \begin{bmatrix} \Delta x \\[1ex] \Delta y \\[1ex] \Delta z \\[1ex] \Delta \tau \end{bmatrix} + \begin{bmatrix} v_1 \\[1ex] v_2 \\[1ex] v_2 \\[1ex] \vdots \\[1ex] v_m \end{bmatrix} $$
Bu sistemi bir $b = Ax + v$ lineer sistemi olarak görebiliriz, ki en az kareler yöntemi sistemi çözer. $A$ matrisinin içeriği için kısmi türevlerin alınması lazım, bu türevler, mesela $P^1$ ve $x$ için
$$ \frac{\partial P^1}{\partial x} = \frac{x^1-x}{\sqrt{ \big( (x^1-x)^2 + (y^1-y)^2 + (z^1-z)^2 \big) }} = \frac{x^1-x}{\rho} $$
Tüm ölçümler ve değişkenler için yapalım,
$$ A = \left[\begin{array}{cccc} \dfrac{x^1 - x}{\rho} & \dfrac{y^1 - y}{\rho} & \dfrac{z^1 - z}{\rho} & 1 \\ \dfrac{x^2 - x}{\rho} & \dfrac{y^2 - y}{\rho} & \dfrac{z^2 - z}{\rho} & 1 \\ \dfrac{x^3 - x}{\rho} & \dfrac{y^3 - y}{\rho} & \dfrac{z^3 - z}{\rho} & 1 \\ \vdots & \vdots & \vdots & \vdots \\ \dfrac{x^m - x}{\rho} & \dfrac{y^m - y}{\rho} & \dfrac{z^m - z}{\rho} & 1 \end{array}\right] $$
Böylece bir $b = Ax + v$ sistemi elde ettik, $\Delta$ değişkenleri bilinmeyen, $A$'yı üstte kurduk, standart en az kareler uygulayınca $v$'yi minimize eden bilinmeyenler bulunacaktır.
Şimdi çözülenin ne olduğuna dikkat, çözümler $\Delta$ değişkenleri, yani $x_0,y_0,z_0,\tau_0$ noktası ile olan fark. Şimdi, bir de Taylor açılımlarının püf noktasını hatırlayalım, bu açılımlar açılım noktası etrafında, yakınında geçerlidir. O zaman nihai çözüme bir döngü içinde erişmek gerekecek, yavaş yavaş, bir önceki çözüme ekleye ekleye. Herhangi bir başlangıç noktası mesela dünyanın merkezi ve sıfır yanlılık $x_0,y_0,z_0,\tau_0 = (0,0,0,0)$ ile başlarız, $\Delta$'ları hesaplarız, ve başlangıca ekleriz, bunlar yeni "başlangıç" noktası olur, hesabı tekrarlarız, ve farklar çok ufak oluncaya kadar (çözüme yaklaştık) bunu tekrar ederiz.
Başlangıç noktasını referans alıp ekleme yaparak hesabın bir ek faydası var; mesela cep telefonu ile yürüme durumunda bir yeri hesapladıktan / kitledikten sonra bir sonraki yer hesabı için tekrar dünya merkezini başlangıç almamıza gerek yok, en son kitlenen yeri başlangıç kabul ederiz, ve büyük ihtimalle tek bir ek hesap ile yeni konumu hesaplayabiliriz.
import matplotlib.pyplot as plt
import scipy.linalg as lin
xtrue = [3507884.948, 780492.718, 5251780.403, 0]
xxyyzz = [[16577402.072, 5640460.750, 20151933.185],
[11793840.229, -10611621.371, 21372809.480],
[20141014.004, -17040472.264, 2512131.115],
[22622494.101, -4288365.463, 13137555.567],
[12867750.433, 15820032.908, 16952442.746],
[-3189257.131, -17447568.373, 20051400.790],
[-7437756.358, 13957664.984, 21692377.935]]
xxyyzz = np.array(xxyyzz)
pseudorange = np.array([20432524.0, 21434024.4, 24556171.0,
21315100.2, 21255217.0, 24441547.2, 23768678.3])
Üstte örnek ölçümler görüyoruz. [6]'daki araştırmacı Danimarka'da bir ölçüm merkezinde GPS aletinden 7 tane GPS uydusuna olan sözde uzaklığı ve bu uyduların o anki yerlerini kaydetmiş, bu kişi acaba nerededir? Tarif edilen yaklaşım ile hesaplayalım,
xx = xxyyzz[:,0]
yy = xxyyzz[:,1]
zz = xxyyzz[:,2]
x = [0, 0, 0, 0]
A = np.ones((len(xxyyzz),4))
for iter in range(20):
rng = np.sqrt((x[0]-xx)**2+(x[1]-yy)**2+(x[2]-zz)**2);
F = rng + x[3]
irange = 1/rng;
A[:,0] = irange*(x[0]-xx)
A[:,1] = irange*(x[1]-yy);
A[:,2] = irange*(x[2]-zz);
c = np.dot(A.T,pseudorange-F)
N = np.dot(A.T,A)
deltahat = lin.solve(N,c)
x = x+deltahat
if np.max(np.abs(deltahat))<0.001: break
print 'iter', iter
print np.reshape(x, (4,1))
iter 4
[[ 3507889.12958827]
[ 780490.02116445]
[ 5251783.75537277]
[ 25511.14592576]]
Döngü beş kez tekrarladı ama dünya merkezinden başlamış olmamıza rağmen sonuca çabukça erişti. ECEF sisteminden enlem / boylam çevirimini yapalım,
import orbital
print orbital.ecef2lla(x)
(55.796250049381591, 12.543735075055356, 73.165498103015125)
Bu kordinatları bir harita uygulamasından kontrol ettik; yazar Danimarka'da teknik üniversite yakınlarında imiş. Zaten [6] gerçek yerini de paylaşmış, üstteki çözüme çok yakın. Sistem işliyor demektir.
GPS uydu uzaklıklarını baz alarak konum hesabı niye faydalı? Cep telefonları zaten enlem / boylam raporlamıyor mu? Bu doğru, fakat farklı mobil uygulamaları farklı şekilde bu hesabı yapmayı, hızlandırmayı seçebilirler. Bu ihtiyaçtan dolayı olmalı Android işletim sistemi tasarlayıcıları 7.0 (Nougat), API 24'ten itibaren ham uzaklık verisini bir arayüz ile geliştiricilere açmaya karar verdi.
Kaynaklar
[1] Federal Aviation Administration, Uydu Pozisyonları, http://www.nstb.tc.faa.gov/incoming/Waas_Sv_Status.txt
[2] Federal Aviation Administration, WAAS Satellite Status, http://www.nstb.tc.faa.gov/RT_WaasSatelliteStatus.htm
[3] Kelso, Orbital Coordinate Systems, Part II, http://celestrak.com/columns/v02n02/
[4] Raspaud, PyOrbital, https://github.com/pytroll/pyorbital
[5] Blewitt, Basics of the GPS Technique: Observation Equations, http://www.nbmg.unr.edu/staff/pdfs/Blewitt%20Basics%20of%20gps.pdf
[6] Nielsen, Least Squares Adjustment: Linear and Nonlinear Weighted Regression Analysis, http://www2.imm.dtu.dk/pubdb/views/edoc_download.php/2804/pdf/imm2804.pdf
[7] Chartcross Limited, GPS Test, https://play.google.com/store/apps/details?id=com.chartcross.gpstest
[8] Raquet, Calculation of GPS PNT Solution, http://indico.ictp.it/event/a12180/session/21/contribution/12/material/0/0.pdf
Yukarı