Elektrik ve Manyetik Etkileşimler - Ders 7

Şimdiye kadar pek çok yaklaşıklama yaptık, mesela sonsuz düzlem bunlardan biri. Ya da bir diske, çubuğa çok yaklaşmak. Peki yaklaşıklama yapma zamanı ne zamandır? Ne zaman bu tekniği kullanmak uygundur? Bahsettiğimiz örneklerde hep iki farklı uzunluk ölçeği olduğuna dikkat edelim. Bu ölçekleri karşılaştırırız, ve biri diğerinden önemli ölçüde büyükse, bu yaklaşıklama için iyi bir zaman olduğunun işareti olabilir. Mesela elimde bir noktasal yük varsa, ve bu yükten belli bir mesafede duruyorsam, bu problemdeki önemli olan tek mesafe noktasal yükten ne kadar uzakta durduğum. Çünkü yük çok ufak, onun uzunluk bağlamında uzaklığa kıyasla bir önemi yok.

Eğer elimizde bir disk var ise, şimdi iki tane ölçekten bahsediyoruz, biri bu disk mesafe, biri diskin ne kadar büyük olduğu. Ne zaman bu şekilde iki ölçek var ise, yaklaşıklama yapabilir miyim diye kendimize sormamız lazım.

Örnek

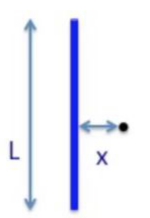
Elimizde bir metal çubuk var, çubuğun uzunluğu $L$. Çubuğun elektrik alanını nasıl hesaplayacağımızı gördük. Çubuk uzunluğu $L=100m$ olsun, ve ben ondan $x=1 mm$ uzakta duruyor olayım.

Ölçekler öyle farklı ki üstteki diyagram aslında temsili değil, gerçek ölçülere yakın çizmeye kalksam $x$ gözükmezdi bile. İşte iki farklı uzunluk ölçeği. Hemen acaba yaklaşıklama yapabilir miyim diye düşünüyorum. İki uzunluğun oranına bakabiliriz, $x/L = 10^{-5}$ ki bu sayı $0.1\%$'den bile küçük. Ben $0.1\%$'i bir eşik değeri olarak kullanırım, ne zaman bir ölçek oranı bu yüzdeden küçükse bunu bir yaklaşıklama işareti olarak algılıyorum ben.

O zaman çubuğun elektrik alan formülünü yazalım (çubuğu kesen düzlem için),

$$ \vec{E} = \frac{1}{4\pi\epsilon_0} \frac{Q}{x \sqrt{x^2 + (L/2)^2}} \hat{x} $$

Eğer bölendeki karekök içindekilere bakarsak bir $x^2$ var bir de $(L/2)^2$ var, birbirleriyle toplanıyorlar. Yaklaşıklama için aradığımız bu tür bir işlem, toplama var, ama işlemdeki bir kısım diğerinden ölçek olarak çok çok farklı. Çarpma değil toplam olması önemli çünkü ufak sayı büyük olana o zaman fazla etki etmez, ama çarpma olsaydı küçük olan sayı nihai çarpımı küçüklüğe doğru çekebilirdi. Devam edelim $L$ ölçeği $x$ ölçeğinden çok daha büyük. O zaman bu problemde $x$'in ne olduğu umrumuzda değil, onu yok sayıyoruz,

$$ = \frac{1}{4\pi\epsilon_0} \frac{Q}{x \sqrt{\cancel{x^2} + (L/2)^2}} \hat{x} $$

ve matematiğe geri kalanlarla devam ediyoruz.

$$ = \frac{1}{4\pi\epsilon_0} \frac{Q}{x (L/2)} \hat{x} $$

$$ = \frac{1}{4\pi\epsilon_0} \frac{2(Q/L)}{x} \hat{x} $$

ve tekrar etmek gerekirse bu çubuğa çok yakın yerlerde, $x << L$ olduğu durumlar için.

Devam edersek şimdi boş ve dolu kürelerin yüklerini hesaplamak istiyorum. Boş küre durumunda bir ince dış tabaka olacak ve yüklerin bu katmanda yüklerin birörnek dağılmış olduğunu düşüneceğiz. Dolu durumda içeride materyel olacak, ve yük bu durumda kürenin her tarafında birörnek dağılmış olacak. Faraziyemiz materyelin yalıtkan olduğu.

Toplam yük hesabını daha önceki gibi yapabilirdik, küre dışı ya da içindeki ufak bir noktasal yükün alanından başlayıp, bunu alansal olarak toplamak, entegralini almak ve toplamı bulmak. Disk, çubuk, vs. için kullandığımız bu yaklaşım bu problemde çok fazla başımızı ağrıtacak. Şimdilik simetri kullanarak hesabın kendisini atlayacağız, bu bir kısayol. Daha ileride Gauss'un Kanunu adındaki bir teknik ile bu hesabı daha hızlı yapmamızı sağlıyor. Şimdi simetriyi kullanalım.

Kürenin simetrisi nerede? Diyagramsal olarak düşünürsem bir küreyi sağa, sola cevirsem hala bir küre değil midir? Fiziğin güzel tarafı eğer diyagramda fark görülmüyorsa matematikte de fark görülmez demektir. Yani bir küreyi çevirmek fiziksel durumda değişikliğe yolaçmaz. Kullanabileceğimiz bir diğer faktör çok uzaktan kürenin noktasal yük gibi gözükeceği.

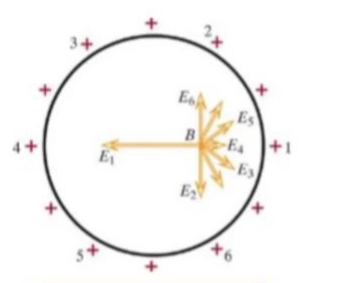
Yalıtkan madde düşünürsek kürenin içindeki elektrik alanı her notada sıfırdır. Bunu ispatsız veriyorum ama alttaki diyagram ikna edici olacaktır. Küre içindeki herhangi bir $B$ noktasını düşünürsek ona etki eden tüm kuvvetler gösteriliyor. Buradan hareketle kürenin içindeki toplam elektrik alan sıfır olacaktır, çünkü her noktayı düşünürsek ortaya çıkan tüm alan etkileri birbirini yokeder.

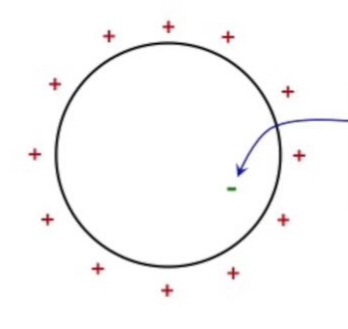
Farazi bir durum sorusu: eğer bu küre içine bir negatif yük koysaydım alan açısından ne olurdu? Hiçbir şey. Yalıtkan madde faraziyesi bize küre içi toplam sıfır elektrik alanı verdi, bu alan içine koyulan negatif yük yerinden oynamaz.

Peki iletken durumda ne olur? Diğer pozitif yükler nasıl davranırlardı? Negatif yüke doğru biraz daha yaklaşırlardı. Tamamen değil ama biraz kayma olurdu, yakın yerlerde daha fazla uzaklarda daha az. Bu kayma olduktan sonra küre içinde bir toplam yük ortaya çıkar, ve negatif yüke bir kuvvet uygulanmaya başlanır ve negatif yük çekilir. Gayri stabil bir durum ortaya çıkar. Bu durumda negatif yük pat diye dış katmana doğru gider.

Şimdi iki küreli duruma bakalım. Yavaş yavaş dolu küre durumuna yaklaşmak istiyorum ama şimdilik iki küreye bakalım. Küreler içiçe geçmiş olsunlar.

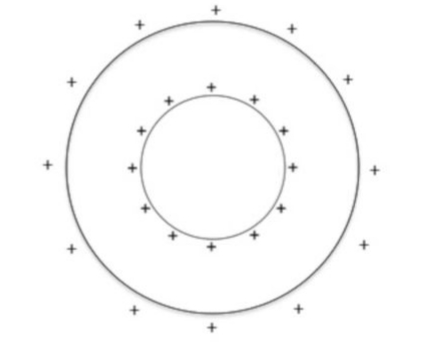
Soru: iki küre arasındaki toplam elektrik alan nedir? Tek kürenin elektrik alanının formülüne bakalım, $R$ yarıçaplı bir küre için, herhangi bir $r$ noktasındaki alan,

$$ \vec{E} = \left\{ \begin{array}{ll} \frac{1}{4\pi\epsilon_0} \frac{Q}{|r|^2} \vec{r} & r>R \textrm{ ise}\\ 0 & r<R \textrm{ ise} \end{array} \right. $$

Yani küre içinde alan sıfır, dışında üstte, ilk satırda görülen formül. Küre içindeyken küre hiç yokmuş gibi düşünebiliriz. İçiçe durumunda yarıçapları $a,b$ olan iki küre olsun, ki $a<b$, arada iken dış kürenin içinde, iç kürenin dışında oluyoruz değil mi? O zaman orada sadece iç küreyi hissederdik, yani

$$ \vec{E} = \left\{ \begin{array}{ll} \frac{1}{4\pi\epsilon_0} \frac{2Q}{|r|^2} \vec{r} & r>b \textrm{ ise}\\ \frac{1}{4\pi\epsilon_0} \frac{Q}{|r|^2} \vec{r} & a<r<b \textrm{ ise}\\ 0 & r<a \textrm{ ise} \end{array} \right. $$

Her iki küre dışında $2Q$ durumu var çünkü her iki kürenin toplam etkisi orada hissediliyor.

Dolu küre durumuna gelelim. Herhalde birazdan yapacağımız tahmin edilebilir; içiçe bir sürü küre düşünürsek, bu bir tür doluluğu temsil edebilir. Diyelim ki bu içiçe kürelerde $r$'de dursak, bu durumda belli miktarda dış küre belli miktarda iç küre var. Bu hesabı nasıl yaparız? Toplam yükü nasıl buluruz?

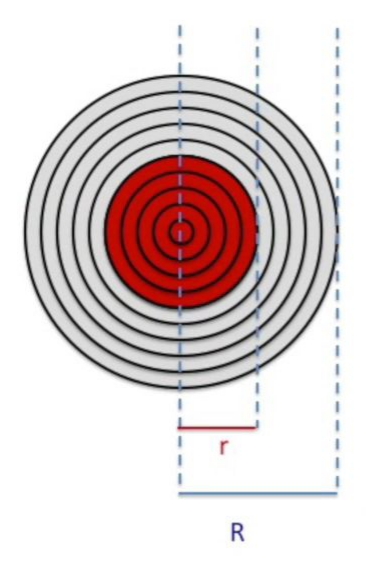
Daha önce iki küre dışında $2Q$ toplam yük demiştik, şimdi tüm içiçe kürelerin toplam yükü $Q$ diyelim. Küre için hacim hesabı $V = \frac{4}{3} \pi R^3$'dir. O zaman alttaki oran da doğrudur,

$$ \frac{Yuk}{Hacim} = \frac{Q}{(4/3)\pi R^3} $$

Daha önce birörnek yük dağılımı vardır demiştik, o zaman bu dolu küreden herhangi bir parçayı çekip çıkarsak o parça için üstteki oran doğru olmalıdır. O zaman $r$ noktasında olan yüke $\Delta q$ dersek, o noktaya kadar olan hacme $\Delta V$, ki $\Delta V = 4/3 \pi r^3$, o zaman $\Delta q / \Delta V$ önceki oranla aynı olur. Yani

$$ \frac{Q}{(4/3)\pi R^3} = \frac{\Delta q}{(4/3)\pi r^3} $$

Bu denklemi tekrar düzenleyerek $\Delta q$ için bir formül elde edebiliriz,

$$ \Delta q = Q \left( \frac{r^3}{R^3} \right) $$

O zaman kırmızı bölgedeki elektrik alanını hesaplayabiliriz, çünkü o noktaya kadar olan yükü biliyoruz,

$$ \vec{E} = \frac{1}{4\pi\epsilon_0} \frac{\Delta q}{r^2} \vec{r} $$

$$ = \frac{Q}{4\pi\epsilon_0} \frac{r}{R^3} \vec{r} $$

Üstteki formül küre içinde olduğumüz sürece geçerli olan bir formül, en iç noktadan başlayıp $r$'yi büyüttükçe lineer olarak elektrik alan artıyor, artıyor. Dışarı çıktıktan sonra tüm kürenin alan etkisi tüm kürenin yarıçapının karesine oranlı azalıyor.