
Elektrik ve Manyetik Etkileşimler dersine [7] hoşgeldiniz. Ben Professor Carlson, ben fiziği çok seviyorum onun için buradayım. Ben teorik fizikçiyim, her gün matematikle uğraşıyorum yani, bu benim işim, dünyanın nasıl olması gerektiğini / olabileceğini anlamaya uğraşmak, teorisyenler bununla meşguldurlar. Bir de deneyci arkadaşlarımız var tabii, onlar dünyanın gerçekte nasıl olduğuyla alakalıdır. Bu iki kanat, biz ve onlar biraraya geliriz sonra, buluşuruz, konuşuruz. Anlaşamadığımız zaman yeni bir şeyler öğrenmemiz gerektiğini anlarız, böyle devam eder.
Fizik size net düşünmeyi öğreten derslerden biridir. Çoğunlukla ufak bir mantıklı prensip demeti olur elimizde, ve bu demeti mantık zinciri kura kura bir sonraki daha büyük anlayışa ulaşmamız mümkün olur.
Başlayalım o zaman. İlk kanun Columb’un Kuvvet Kanunu.

Bu kanun iki yüklü parçacık birbirinin yakınına gelince ne olduğunu kontrol eder.
Bildiğiniz gibi etrafınızda dokunabildiğiniz herşey atomdan yapılmıştır. Atomların içinde yüklü parçacıklar vardır, atom çekirdeği içinde protonlar ve nötronlar vardır ki protonlar artı yüklüdür, çekirdeğin etrafında koca onu dairesel şekilde kaplayan elektronlar vardır, elektronlar negatif yüklüdür. Maddelerin temeli budur. Bazı diğer parçacıklar da var ama etrafımızda dokunabileceğimiz maddelerin çoğunluğu bu tarif ettiklerimden oluşuyor. Yani etrafta bir sürü pozitif ve negatif yüklü parçacıklar var. Bir masaya dokunduğum zaman mesela benim elektronlarım masadaki elektronlara dokunuyor. Dokunma ile hissettiğim bu etkileşim. Columnb’un Kuvvet Kanunu, büyüklükler üzerinden,
\[ |\vec{F}| = F = \frac{1}{4\pi \epsilon_0} \frac{|Q_1 Q_2|}{r^2} \]
Bu formül şunu söylüyor: iki yüklü parçacık birbiri üzerinde bir kuvvet uygular. Bu kuvvetin büyüklüğü [mutlak değer olarak] bir sabit (\(\frac{1}{4\pi \epsilon_0}\) ifadesinin tamamını bir sabit olarak aklımızda tutabiliriz, sabitin birimininde yanlış yapmamak suretiyle) çarpı yük bir çarpı yük iki bölü \(r^2\), ki \(r\) iki parçacığın birbirine olan mesafesi. Vektörel olarak
\[ \vec{F} = \frac{1}{4\pi \epsilon_0} \frac{Q_1Q_2}{r^2} \hat{r} \qquad (1) \]
\(\hat{r}\) kuvvetin etki yönü için eklenmiş, bu yön \(\vec{r} = \vec{r}_2 - \vec{r}_1\) yönüdür, daha doğrusu \(\vec{r}\)’nin birim vektor hali \(\hat{r}\)’dir.
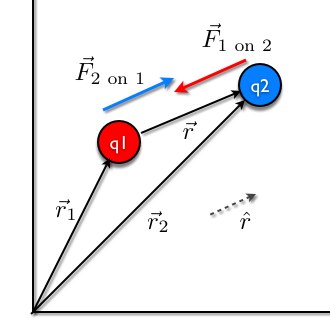
Not: Yük (charge) \(q\) ile gösterilmiş, bu nedir? Yük pek çok elektrondan oluşur, ve columb birimindedir. Tek elektronun sahip olduğu yük Milikan Yağ Deneyi sayesinde biliniyor ve bu \(-1.60 x 10^{-19}\) columb’dur. Yazının sonunda bu deneyi anlatıyoruz.
İki parçacık arasındaki kuvvet bu parçacıkların yüküyle doğru orantılı, ve aralarındaki mesafenin karesi ile ters orantılı. İki parçacığı alıp birbirlerinden uzaklaştırmaya başlasam gittikçe aralarındaki çekimi daha az hissederim değil mi? Bu mantıklı değil mi? Bu azalma \(1/\textrm{mesafe}^2\)’ye oranlıdır. Fizikteki pek çok kural \(1/\textrm{mesafe}^2\)’ye oranlı azalır bu arada, yani bu kavramı “arkadaş edinmek’’ iyi olur.
Kuvvet yönü ters işaretli yükler için birbirine doğru, aynı işaretler için, iki negatif ya da iki pozitif olabilir, birbirinden ters yönde.

Ama her halukarda kuvvet her zaman iki yükün arasında direk çizilebilecek bir hayali çizgi üzerindedir, bu çizginin iki yükün merkezinden geçtiği düşünülebilir.
Kullanacağımız birimler SI birimleridir, elektrik yükü Coulomb, \(C\).
\(\epsilon_0 = 8.85 x 10^{-12} C^2/N m^2\), elektriksel geçirgenlik (permittivity) sabiti,
\(1/4\pi \epsilon_0 = 9 x 10^9 N m^2 /C^2\), ki bu sabit birimlerin düzgün çıkması için kullanılır. Eşitliğin solunda gereken bir birim var, sağında belli birimler biraraya geliyor, sabit bunların hepsini tercüme eder.
En temel yük birimi [Millikan deneyinden],
$ e = 1.602 x 10^{-19}$
Bakacağımız her parçacık bu temel yük birimini baz alır, yükleri bu sayının katlarıdır. Mesela elektronlar \(-e\) katlarındadır, protonlar \(+e\).
Şimdi bize elektrik alan (electric field) denen bir kavram lazım.
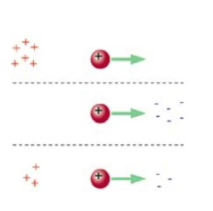
Diyelim ki bir pozitif yüklü parçacık var. Eğer bu parçacığı, nesneyi bıraksam ve bu nesne 9.8 \(m/s^2\) hızında aşağı düşse, bunun sebebi olarak aklınıza ilk gelen şey ne olurdu? Yerçekimi tabii. Bazen hepimizin başına gelmiştir, [düşmek üzere olan birinin taklidini yapıyor] kulak etrafınızdaki algılayıcılar der ki “98 \(m/s^2\) ile aşağı iniş var’’, biz de hemen elleri uzatıp küt diye düşmekten kendimizi kurtarmış olabiliriz.
Peki eğer şimdi bu parçacığı bıraksam pat diye yan duvara doğru gitse? Bunun sebebinin yerçekimi olduğunu düşünmezdim değil mi? Başka bir şey buna sebep olurdu. Eğer elimdeki yüklü bir parçacık ise büyük bir ihtimalle sebep yakındaki diğer yüklü parçacıklar.
Peki detayda nasıl? Belki parçacık yan duvarın karşısındaki pozitif yüklü pek çok parçacık tarafından itiliyor, o sebeple gördüğümüz hareket oluyor, ya da gittiği yöndeki duvarda negatif yüklü parçacıklar var, onlar çekiyor. Bu hareketin ortaya çıkmasının pek çok şekli var, o sebeple pek çok durumu tarif eden, daha evrensel kavramlar üzerinden, elektrik alanı kavramını kullanarak düşünmemiz daha iyi olur.
Ana fikir ortada bir alanın olduğu ki bu alan birim yük üzerinde etki eden kuvvettir. Parçacık niye hareket etti? Bu parçacık olsa da olmasa da ortada, parçacığın içinde olduğu uzayda etkili olan bir şey vardı, o şey bu alandı. Bu alan içine gelen parçacığı itmek ya da çekmek için orada hazır bekliyordu.
O zaman test parçacığının hızlandığını (ivme var) görüyorsam, bu parçacık üzerinde belli bir kuvvet var demektir, ve bu kuvvet test parçacığın yükü çarpı şimdi elektrik alanı diyeceğimiz bu diğer şeyin sonucuna bağlı olacaktır. Bu şey, bu kuvvete sebep olan bu oluş, elektrik alanının tanımıdır.
\[ \vec{F} = q \vec{E} \qquad (2) \]
İki tarafı \(q\) ile bölersem,
\[ \vec{E} = \vec{F} / q = \left[\frac{Newton}{Coulomb}\right]\]
Alanın birimi newton/coulomb’dur, ileride göreceğiz ki volt/metre de kullanılabilir.
Peki şimdiye kadar bir elektrik alanını birince elden deneyimlemiş olanlarınız var mı? Onu hiç hisseden farkeden oldu mu? [Öğrenci cevap verdi]. Evet, arkadaşınızın dediği gibi, mesela belki bunu kendiniz yaptınız ya da yapan arkadaşınızı gördünüz, mesela bir balonu aldınız, kafanıza sürttünüz, sürttünüz, ondan sonra duvara koydunuz, ve baktınız ki balon duvara yapışık kaldı! Bu deneyi şu anda sınıfta yapmayı çok isterdim ama bugün müthiş nemli bir gün, daha kuru bir havada deneyin başarı şansı daha fazla.
Evet bu statik elektriği deneyimlemenin bir yolu. Başka yol var mı? Hissetme duyumuzla mesela? Daha önce bahsettiğimiz gibi dokunma duyumuz elektrik alanına bağlı, ben elektronlar, protonlar ve nötronlardan oluşuyorum, ve dış yüzeyim, dışarısı ile temas eden elektronlar [çünkü atomların dış cepherinde onlar var atomları bir bulut gibi sarmalıyorlar]. Bir şeye dokunduğumda benim elektronlarım dokunduğum şeylerin elektronlarına dokunuyor, ve bu “Coulomb itişini’’ [temeli elektriksel olan] sinir sistemim ile hissediyorum.
Başka bir yol? [Bir öğrenci ‘gözler’ diyor]. Gözler, evet. Bunu açıklayabilir misin [cevap veriyor]. Evet dediği gibi bizim ışık dediğimiz aslında elektrik. Işığın yayılmasına sebep olan bir manyetik alanla beraber bir elektrik alandır, bu örneğin ilk değil 5., 6. örnek olarak aklımıza gelmesi ilginç aslında, ve yerinde bir bakıma, çünkü insanlığın pek çok elektriksel sonucun aynı sistemin parçası olduğunu keşfetmesi çok uzun zaman aldı. Aynı derken balonu kafamıza sürtüp duvara koymak ya da şaka amaçlı halıda sürte sürte yürüyüp arkadaşımızla tokalaşmak ve o sırada elektrik şoku yaşamak, ve gözümüzde hissettiğimiz ışığın aynı şey olduğunu kavramaktan bahsediyorum. Bu kavramsal birleştirme biz insanlar için uzun zaman aldı.
Yani elektrik alanlar aslında her tarafımızda, onlar her yerde. Onları sürekli deneyimliyoruz, bazen bilinçli olarak çoğu zaman farkında olmadan. Hatta bizim gözlerimizin algılayabildiği ışık olarak deneyimlediğimiz elektromanyetik alanlar aslında sınırlı bir frekans aralığından geliyor, değil mi? Doğadaki bazı hayvanlar bizim gördüğümüz frekans aralığından daha geniş bir alanı algılayabiliyor. Kimisi kızılötesini (infrared), kimisi morötesini (ultraviolet) görüyor mesela. Tabii özel cihazlar, mesela özel bir gözlük kullanarak biz de bu aralıkları görebiliyoruz.
Devam edelim, alttaki gibi iki pozitif yüklü parçacık var elimizde diyelim, denklemler negatif için de işler ama ben akıl yürütme, test amaçlı olarak pozitif yükle başlamayı daha faydalı buluyorum.
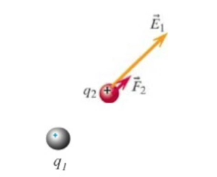
Ve yine diyelim 1. parçacık yerinde sabit tutuluyor, ama 2. parçacık serbest. Bu parçacık \(\vec{F}_2\)’yi hissedecek yani 2. parçacık üzerinde etki eden kuvvet. Bu durumu Coloumb kuvvet kanunu ile nasıl temsil edeceğimizi biliyoruz, (1). denklemi hatırlayalım. Diğer yandan (2). denkleme göre kuvvet etrafta olan elektrik alanına da doğru orantılı. Bu iki fikri birleştirirsek, 2. parçacığı inceliyorum, ona etki eden elektrik alanı 1. parçacıktan geliyor olmalı, her iki denklemde kuvvet var, ve bu kuvvet aynı kuvvet. (2) bu örnekte şöyle,
\[ \vec{F}_2 = q_2 \vec{E}_1\]
\[ \vec{E}_1 = \frac{1}{4\pi \epsilon_0} \frac{q_1}{r^2}\hat{r} \]
İşte bu \(q_1\)’in ürettiği elektrik alan.
Eğer \(q_2\)’yi iki boyutlu uzayda gezdirseydim ve ona etki eden elektrik alanın her zaman 1. parçacıktan dışarı yönde olduğunu bulurdum (alt soldaki resim).
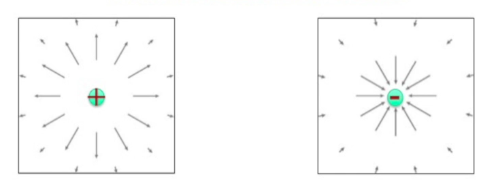
Tüm bu okların birarada gösterirsem elektrik alanının genel görüntüsünü elde edebilirdim. Pozitif yüklü parçacığın yarattığı alanın her zaman dışarı doğru olduğuna dikkat, ben hatırlama numarası olarak “pozitif insanlar hep başkalarını düşünürler [oklar onlara doğru bu sebeple]’’ diye bir cümle yarattım aklımda (!) sizin için de faydalı olabilir belki. Negatif için ters yönde,”negatif insanlar sadece kendilerini düşünürler’’.
Her yönde giden bu okların olduğu resim önemli, elektrik alanı bir tür kirpi gibi düşünüyoruz, dikenleri her yönde gidiyor, tabii uzaklaştıkça daha inceliyor bu dikenler [etkileri azalıyor].
Örnek
\(q_1 = 2nC = 2 x 10^{-19} C\) büyüklüğünde bir yüke sahip parçacık orijinde duruyor. Gözlemlenen yer (observed location), \([-0.2, -0.2, -0.2]\) metre noktasında, buradaki elektrik alanı nedir? Kusura bakmayın eksenleri çizmeyi unutmuşum, ama parçacığı (source location) orijinde düşünün, \(x,y\) yana ve yukarı gidiyorlar, \(z\) bize doğru geliyor.
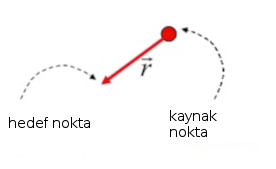
\(r\) bana doğru işaret ediyor unutmayalım, ve vektörsel büyüklükler bağlamında, bir vektörün bir yön ve ve büyüklükten oluşan bir kavram olduğunu hatırlayalım. Bu derste sizden bir vektör sonucu hesaplamanız istendiğinde bunu iki şekilde yapabilirsiniz, ya salt yön (birim vektör üzerinden) çarpı tek sayısal büyüklük, ya da tek vektör içinde kendi başına hem yön hem de büyüklüğü belirtebilen bir sonuç olarak.
Neyse bizden elektrik alan hesaplamamız istendi ki bu bir vektördür (o sebeple \(E\) sembolünün üzerinde bir ok var, \(\vec{E}\) şeklinde). Bu tür hesapları yaparken benim ilk yaptığım iş \(\vec{r}\)’yi hesaplamak, ki bu hedef yeri eksi kaynak yeri olarak hesaplanır. Hedef \([-0.2, -0.2, -0.2]\) demiştik, kaynak orijin, yani \([0.0, 0.0, 0.0]\).
O zaman
\[ \vec{r} = [-0.2, -0.2, -0.2]-[0.0, 0.0, 0.0]=[-0.2, -0.2, -0.2] \]
Birim yön için büyüklüğü hesaplayıp üstteki vektöre böleriz,
\[ |\vec{r}| = \sqrt{(-0.2)^2 + (-0.2)^2 + (-0.2)^2 } = 0.35 m\]
\[ \hat{r} = \frac{\vec{r}}{|\vec{r}|} = \frac{[-0.2, -0.2, -0.2]}{0.35} = [-0.57, -0.57, -0.57] \]
Bu arada \(\hat{r}\) birimsizdir, bu mantıklı çünkü sadece bir yöne işaret etmek için hesaplandı. Şimdi elektrik alanı formülü ile alanın bahsedilen noktadaki büyüklüğünü hesaplayalım,
\[ E = \frac{1}{4\pi \epsilon_0} \frac{q_1}{r^2} = \left( 9 x 10^{9} \frac{Nm^2}{C^2} \right) \left(\frac{2 x 10^{-9} C}{0.35^2} \right) = 147 \frac{N}{C} \]
Vektör formunda
\[ \vec{E} = E \vec{r} = \left( 147 \frac{N}{C} \right) [-0.57, -0.57, -0.57] \]
\[ = [-0.84, -0.84, -0.84] \frac{N}{C}\]
Ekler
Milikan Yağ Damla Deneyi
Tek bir elektronun yükü nedir? Acaba birim yük denen bir şey var mıdır? Amerikalı bilimci Robert Millikan bu soruların cevabını bulmak için kolları sıvadı. Tasarladığı deneye göre yağ damlaları bir ölçüm aletine yukarıdan damlatılıyor, ya da bir aletten püskürtülüyordu, ve damlalar iki elektrik plakası arasına gidiyordu. Plakalar bir elektrik kaynağına bağlıdır, yani onlara eksi ya da artı yönde değiştirilebilir bir voltaj uygulanabiliyor (böylece damlalara etki eden elektrik alanı önceden biliniyor), ve değişik voltajlarda yağ püskürtülerek ne olduğuna bakmak mümkün oluyordu. Burada amaç damlaların elektron miktarını bir şekilde ölçmekti, tabii ekstra ya da kayıp elektronlar sahip olunması istenen bir şeydi ki elektrik alanı ile etkileşim daha rahat ortaya çıkabilsin, bu ekstra ya da kayıp elektronların yağ püskürtülürken hava ile olan sürtünme üzerinden, ya da bazı deneylerin yaptığı bir ilerlemeyle, dışarıdan iyonlaştırıcı ışıma (ionizing radition) ile bombardımana tutularak kazanmaları planlanıyordu.
Üniversite ilk sınıf için yapılan bir basitleştirme yağ damlalarının bir plastik kapsül içinde ve standard boyda, bu aşağı yukarı 1 mikrometre (\(\mu m\) ya da mikron) ve ağırlığı \(m = 5.7 x 10^{-16}\) kg. olması. Millikan’ın deneyinde elektrik alanın çekmesi, itmesi ile yavaş yavaş yukarı çıkan, ya da düşen damlaların hızları ve (standard olmayan) boyutları ölçülerek hesaplar yapılıyor. Daha basitleştirilmiş deneyde sadece havada asılı kalan standard damlalara bakılıyor.
Ana formüller \(\vec{F} = q \vec{E}\) ve yerçekim \(m\vec{g}\). Eğer bir damla askıda ise yukarı çeken elektrik alan kuvveti ile yerçekim eşittir demektir, yani
\[ q \vec{E} = -m\vec{g}\]
Tabii deney sırasında her veri noktası için değiştirilen ve kaydedilen voltajdır, üstteki formülü içinde voltaj barındıran formüle çevirmek için \(E = V / d\) üzerinden
\[ q = \frac{m g d}{V}\]
elde edilecektir. Bu şekilde yapılan deneylerde [3, sf. 89] asılı kalan damlalara uygulanmış voltaj altta görülebilir. Bu veriye üstteki \(q\) formülü uygulanır, \(m\) biliniyor, plakalar arasındaki mesafe \(d = 4.0 mm\).
\(q\)’ler elde edilince ilk yaptığımız \(|q|\) değerlerinin bir histogramını hesaplamak. Acaba yük değerleri belli değerler etrafında öbekleniyor mu? Belli kutulara düşüyorlar mı? Belki bu sayede onların belli tek bir birim yükün katları olduğunu bulabilirdik.
import pandas as pd
data = [-30, 28.8, -28.4, 30.6, -136.2, -134.3, 82.2, 28.7,\
-39.9, 54.3, -126.3, -83.9, -44.6, -65.5, \
-139.1, -64.5, -28.8, -30.7, 26.1, -140.8, -31.5, -66.8, 41.5,\
-34.8, -44.3, -143.6, 77.2, -39.9, -57.9, 42.3]
df = pd.DataFrame(data)
df.columns = ['V']
d = 4e-3;
g = 9.81
m = 5.7e-16;
df['q'] = m * g * d / df.V
df['q'] = np.abs(df.q)*1e19
ax = plt.hist(df.q ,bins=50)
plt.savefig('elecmag_02.png')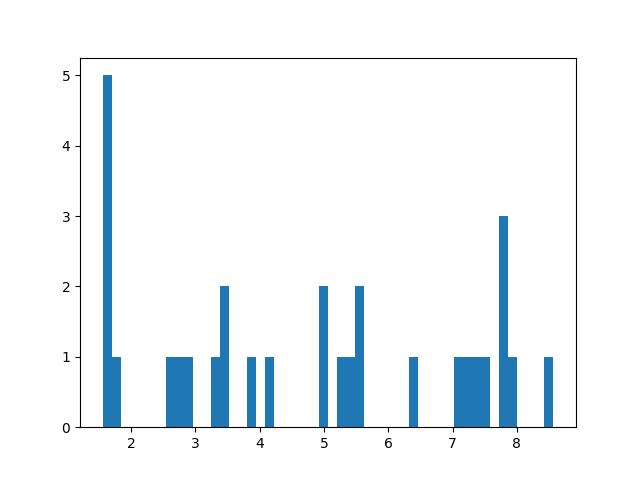
Histograma göre böyle bir gruplama var gibi duruyor. Şimdi grupları içine bir tepe noktası düşecek şekilde ayıracak sınır noktalarını bulup, aralıklara düşen değerlerin ortalamasını alırsak,
m1 = df.q[df.q < 2.5].mean()
m2 = df.q[(df.q > 2.5) & (df.q < 4.0)].mean()
m3 = df.q[(df.q > 4.0) & (df.q < 5.5)].mean()
m4 = df.q[(df.q > 5.5) & (df.q < 7.5)].mean()
m5 = df.q[(df.q > 7.5) & (df.q < 8.0)].mean()
print (m1,m2,m3,m4)1.6387763052353757 3.1968559766438944 4.972056517681478 6.684265107125632Ayraç değerlerini kabaca seçtik, öyle ki iki ayraç arasında bir tepe noktası olsun ve diğerlerinden aşağı yukarı eşit uzaklıkta olsun.
Neyse görülüyor ki değerler bir şeylerin katı olabilir. O zaman birbirini takip eden değerlerin farkını alırsak, ve bu farkların da ortalamasını alırsak belki bir birim yükü elde ederiz.
ms = [m1,m2-m1,m3-m2,m4-m3]
print (np.mean(ms))1.671066276781408Yani sonuç \(1.67 x 10^{-19}\) çıktı. Gerçek sonuç \(1.60217662081 x 10^{-19}\) değeridir. Fena değil!
Elde edilen elektron yükü birimsizdir (kimyadaki mol gibi). Peki 1 Coulomb içinde kaç elektron vardır o zaman? Bu hesap için 1 değerini üstteki sonuçla bölersek (yani tersine çevirirsek),
e = 1.60217662081e-19
print (1.0/e)6.24150912584e+18sonucu elde edilir. Bu sayı ünlü bir sayı, Avogadro’nun Sayısı olarak ta biliniyor.
Ödev
Milikan deneyini simülasyon ortamında yapmak için [1] kullanılabilir (orijinali [2]’de). Bu deneyin üstteki ölçümlerden bir farkı damlaların farklı boyutta olabilmesi, püskürtme sonrası hareketsiz kalan bir yağ damlasına mercekle bakılıyor ve onun çapı ölçülüyor. Bu çaptan hacim, hacimden kütle \(m\) hesaplanabilir. Ödeviniz bu deneyi yeterince damla için yapmak, her yağ damlası için farklı olan \(m\)’leri kullanarak ve üstteki yaklaşımla birim yükü tekrar hesaplamak.
Volt, Amper, Watt
Elektriği şu gibi düşünürsek amper akan şu miktarı (belli bir zaman aralığında), volt ise suyun basıncı (hareket etmekte olan her şu molekülünün arkasındaki itiş kuvveti, çünkü bir şeyin hızı ile onun arkasındaki kuvvet farklı olabilir) [8]. Amperi yük akışı gibi düşünebiliriz, bir güç kaynağından çıkan elektron sayısı, oran olarak, belli bir zaman aralığında.
Volt her yükün enerjisi. Güç kaynağının bu yükleri ne kadar kuvvetle ittiği bir anlamda. Her iki ölçütün ortak noktası yük, yani Çuloumb (C). Amper bir saniyedeki yük, yani Coulomb / saniye, A = C/s. Volt ise Joules / Coloumb, V = J/C. Elektrik gücü elde etmek için bu ikisini çarparız, ve W = A * V = C/s * J/C = J / s, yani Joule / saniye, ki bu gücün tanımıdır.
Alternatif Anlatım
Coulomb hesabı yapıyoruz, fakat bu hesabın temel aldığı mesela voltaj nerede geliyor? 1 Volt’u kim tanımlamıştır? Ya da ondan önce 1 Amper nedir?
Bunun için Ampere’in Kuvvet Kanunu [4] bilmek gerekir. Bu kanun yeterince temeldir,
\[ \frac{F_m}{L} = 2 k_A \frac{I_1I_2}{r}\]
Yani birbirine paralel iki iletken düşünüyoruz, bu iki iletkenin birim uzunlukta birbirine uyguladığı kuvvet üsttekidir. Aslında bu uygulanan kuvvet \(F_m/L\) hangi iletken daha kısaysa o kabul edilir, daha uzun olan iletkenin sonsuz olduğu farz edilir, \(r\) iki iletken arasındaki mesafedir.

\(k_A\)’yi biz (bilimciler) seçiyoruz. Ayrıca \(k_A\)’yi bir başka sabit \(\mu_0\) ile ilintilendirmişler,
\[ k_A \mathrm{tr}iangleq \frac{\mu_0}{4\pi}\]
ve
\[ \mu_0 \mathrm{tr}iangleq 4\pi x 10^{-7} N / A^2\]
Devam edersek, 1 Amper \(r = 1\) metre seçildiği zaman, üstteki sabit üzerinden \(2 x 10 ^{-7} N/m\) sonucunu verecek şeydir. Her iki iletkene bu aynı “şey’’ verilir, ve 1 Amper budur. Peki ama kuvvet ölçmek zor değil mi? Zor değil. Newton bazlı kuvvet ölçümü mümkün, iletken, tel üzerindeki itme, çekme gibi etkiler bir aletle ölçülebilir.
1 Newton 1 kg kütleyi saniye karede 1 metre ivmelendiren kuvvete denir.
1 Amper 1 Coulomb yükün 1 saniyede akmasıdır.
1 Volt çinko sülfat ve bakır sülfat sıvıları hazırlanıyor, ve içlerine bakır ve çinko elektrotlar sokuluyor. Bu sıvı bir elektrik üretir ve bilimciler bu yapının ürettiği elektriği 1 Volt olarak kabul etmiştir [5, 6]. Altta görülüyor, voltmetre bağlanınca tam 1 V çıkıyor (-1 diyor ama ölçüm kablolarını değiş tokuş yapsa +1 V olur)

Kaynaklar
[1] Millikan Yağ Damla Deney Labaratuarı (Yerel Kopya), https://burakbayramli.github.io/dersblog/elecmag/elecmag_01/millikan.html
[2] Millikan Oil Drop Lab, http://www.thephysicsaviary.com/Physics/Programs/Labs/MillikanOilDropLab/index.html
[3] Thornton, Modern Physics for Scientists and Engineers
[4] Wikipedia, Ampère’s force law, https://en.wikipedia.org/wiki/Amp%C3%A8re%27s_force_law
[5] Wikipedia, Daniel Cell, https://en.wikipedia.org/wiki/Daniell_cell
[6] Powell, Daniell cell - Volt Defined, https://www.youtube.com/watch?v=HVLgydntcSU
[7] Carlson, Prof. Carlson, YouTube Kanalı, https://www.youtube.com/channel/UCCkXe14p5a5udg75GhVbN7Q/videos
[8] Quora, https://www.quora.com/What-is-the-difference-between-volts-and-amps
[12] https://www.bixpower.com/Battery-Cell-Chemistry-Comparison-s/2392.htm
[13] https://www.rapidtables.com/calc/light/how-lumen-to-watt.html