Daha Az Kumandalı Robotlar

HONDA şirketinin Asimo adlı robotu 1996 yılında ortaya çıktığında herkes robotik konusunda önemli bir noktaya erişildiğini anlamıştı. Asimo rahat bir şekilde yürüyor, merdiven çıkıyor, hatta futbol oynuyordu [1, 3:50]. Fakat robotun hareketlerine yakından bakarsak bir ayağının sürekli düz şekilde yerde olduğunu görüyoruz, robot sanki kendi dinamiği ile barışık değil / ondan istifade etmiyor. Çok muhafazakar bir şekilde hareket ediyor, ve her hareketinin her noktası planlı, ve güvenli.

Bu niye tercih edilir değil? Öncelikle çok fazla enerji sarfediliyor, Asimo'nun yürüyüşü normal insanın yürüyüşüne kıyasla 20 kat daha fazla enerji gerektiriyor, bu sebeple büyük bir pil taşıması gerekiyor ve o pil bile ancak yarım saat yetiyor.

Pek çok açıdan Asimo fabrikalardaki robot işçi kolların evriminin vardığı nihai nokta. Yüksek kazançlı (bunun anlamını ileride göreceğiz) bir sistem, aynen fabrika robot kollari gibi çok miktarda enerji ve geri besleme kullanıyor, ve üzerinde çok detaylı düşündüğü planladığı bir aksiyonu uyguluyor.

Ama yürümenin farklı yolları var. Mesela insanların yürüyüşü aslında bir nevi "kontrollü düşüş" denebilir. Yani insanlar çevre dinamiğine, çevrenin fiziğinden istifade ederek yerçekim, yukarı gidiş, sürtünme arasında bir optimal nokta bulup az mıktarda bir kontrol uygular, ve bu şekilde yürür. Mesela şuradaki robot [1, 7:22] pasif dinamik yürüyüş sergiliyor, bu robot dış enerji bile kullanmıyor, sadece yerçekiminden istifade ederek düşmeden, aşağı yürüyor. Bu robotun yürüyüşü insan yürüyüşüne daha çok benziyor aslında. Robot bize şunu sergiliyor, yürümek için etrafın dinamiğini aşırı kontrol, aşırı geri beslemeli müthiş planlı bir gidiş yoluyla sıfırlamak yerine o dinamiği daha yakından inceleyebiliriz. Burada bütün işi yapan robotun kontrol dinamiği, bilgisayar yok, kontrol sistemi yok.

[Uçuş, denizaltı örnekleri atlandı]

Doğada gördüğümüz çok verimli çalışan örnekler bir bakıma daha az kumandalı (underactuated) denen sistemler. Dersimizin ana konusu bu. Amacımız insan gibi koşan, kartal gibi inen robotlar yapmak. Şimdi daha az kumandalı tarifi ile ne demek istediğimi daha detaylı şekilde anlatmaya uğrasayım.

Bir örnek görelim, iki bağlantısı olan bir robot kol.

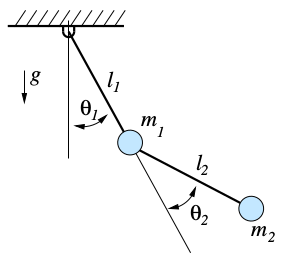
İki uzunluk, iki acı var burada. Ders boyunca $q$ ile robotun kordinatları kastedilecek, örneğimiz için bu kordinatlar $\theta_1,\theta_2$. Büküm noktalarına kontrol $u$ amaçlı bir dönme kuvveti (torque) uygulayabildiğimiz düşünelim, bunları üstten alta doğru $\tau_1,\tau_2$ ile gösterelim.

$$ q = \left[\begin{array}{r} \theta_1 \\ \theta_2 \end{array}\right], \quad u = \left[\begin{array}{r} \tau_1 \\ \tau_2 \end{array}\right] $$

Bu sistemin, bu şarkacın nasıl hareket ettiğini tarif etmek istiyorsak, bu derste ilgilendiğimiz çoğu robot ikinci derece sistemler. Herşeyi kontrol eden ünlü,

$$ F = ma $$

formülü. Bu örnekte $a$, $q$'nun ikinci türevi olacak. $\dot{q}$ birleşik hız, $\ddot{q}$ birleşik ivme. Bu sistemin ivmelenmesini mevcut yer, hız, ve kontrol girdisi üzerinden tarif eden bir formüle ihtiyacım var. İkinci seviye mekanik dünyada yaşıyorsak, şöyle bir denklem lazım,

$$ \ddot{q} = f(q,\dot{q},u,t) $$

Bu dersin aşağı yukarı tamamında üstteki türden gayri lineer bir denklemle temsil edilen ikinci derece sistemlere bakacağız. Hatta bizim ilgilendiğimiz çoğu robot daha da basit bir formda olabiliyor, hareket denklemleri $u$ bazında lineer olabiliyor, robota dönme kuvveti ekleyince bu etki sistemin ivmesine lineer bir etki uyguluyor yani.

$$ \ddot{q} = f_1 (q, \dot{q}, t) + f_2 (q, \dot{q}, t) u \qquad (1) $$

Pek yeni bir şey söylemişim olmadım aslında, $f_1$ ile bir takım gayrı lineer ilişkilerle görülen değişkenler sisteme etki ediyor, sonra $f_2$ ile yine bir takım gayrı lineer ilişkilerle bir ilişki daha var, tek değişik söylediğim $u$'nun lineer olarak etki ettiği.

Devam edelim, tamamen kumandalı ne demek? Üstteki denkleme bakalım, $q$ bir 2x1 vektör, tabii ki $\ddot{q}$ da öyle, yani (1)'de gördüğümüz bir vektör denklemi. $f_1$ aynı şekilde. $u$ da öyle, 2x1 vektör. Bu durumda boyutların uyması için $f_2$'nin 2x2 matris olması gerekir. Hayatı kavramsal, düşünüş olarak en kolaylaştıran, ve çoğu robot tasarımcısının yaptığı $f_2$ matrisinin tam kerte olduğunu düşünmektir. O zaman deriz ki eğer $f_2$ tam kerte ise bir robot tamamen kumandalıdır. Matematiksel olarak,

$$ \mathrm{rank} [f_2(q,\dot{q},t)] = \mathrm{dim} [q] $$

Bu demektir ki eğer $f_1,f_2$'yi biliyorsam $u$ ile istediğim $\ddot{q}$'yu elde edebilirim. Değil mi? Tam kerte bu demek, eğer $f_2$ tam kerte olmasa, tüm uzayı kapsayazdım, çünkü içinde tekrar eden kolonlar olurdu ve bu tekrar yeni bilgi eklemezdi, bu sebeple belli bir $u$ ile her $\ddot{q}$'ya erisemezdim.

Daha az kumandalı nedir? Eğer

$$\mathrm{rank} [f_2(q,\dot{q},t)] < \mathrm{dim} [q] \qquad (2)$$

ise.

[geri besleme lineerlestirme atlandi]

Tarif edersek, bir sistemin kontrol girdisi sistemi her yönde ivmelendiremezse o sistem daha az kumandalıdır.

Bu arada (2) formülüne dikkatle bakarsak, $f_2$, $q,\dot{q}$'a bağlı, o zaman daha az, tam kumandalı olma olmamama irdelemesi o anki konuma bağlı. Sistem dinamiği sırasında bazen tam kumandalı olabilirim, bazen olmayabilirim. Bu nasıl olur? Bir engel vardır belki, dinamiği belli şekillerde değiştirir, ve bazı şeyler mümkün olur, bazıları olmaz...

Asimo örneğine dönersek çok dikkatli, muhafazakar bir şekilde hareket ediyor değil mi? İşte bu şekilde dikkatli olarak tam kumandalı konumlarda kalmaya uğraşıyor, yaptığı bu.

Umarım bu tarif ettiğim ayrımın ne kadar derin olduğunu anlatabilmişimdir. Robotik alanında bu fark her yerde; son 30 senedir çoğu araştırmacı robot kontrol tasarlarken $f_2$'nin tam kerte olduğunu farzetmiştir. Mesela uyarlanır (adaptıve) kontrol, hesaplanan dönme kuvveti metotları, tüm bunlar dolaylı olarak bu tam kerte faraziyesini yapar, ki böylece kafanıza esen şekilde kontrol uygulayarak kafanıza esen şekilde ivme yaratabilesiniz. İşte bu sebeple uyarlanır kontrolde mesela tüm bu matematiksel ispatlar vardır, ki sistemi lineerize edebilesiniz, onun hakkında kolay şekilde düşünebilesiniz.

İşte bu sebeple tam ile daha az kumandalı sistemler, tasarımcılar arasında bu kadar ayrılık var, çünkü eğer gayrı lineer sistemi alıp lineer hale getirme şansımız yoksa, o zaman gayrı lineer dinamiği anlamaya uğraşmaktan, onun uzun vadeli davranışı hakkında düşünmekten başka bir şansınız yoktur. Analitik yaklaşımlar neredeyse ise başlar başlamaz ise yaramaz hale gelir, bilgisayarlar burada yardım edebilir.

Fabrikadaki montaj bantında çalışan robot kolların çoğu tam kumandalıdır, yürüyen robotların çoğu değildir.

[atlandi]

Daha Az Kumandalı Robotlar - 3

Önceki derste gayrı-lineer dinamikten bahsettik, faz grafiklerine baktık, çekim bölgesine (basın of attraction) baktık, sabit noktalara baktık.. Kontrol konusuna hafifçe dokunduk ve bu konuya işaret ederken onu bir takım matris denklemlerinin manipülasyonu olarak değil, faz grafikleriyle alakalandırmaya uğraştım, öyle ki kontrol demek bu faz grafiklerini değiştirmek, onları hareket ettirmek demek oluyordu, sistemi kendi istediğiniz noktaya kanalize etmek için grafiği (sistemi) tekrar şekillendirmiş, eğip, bükmüş oluyorduk. Tabii biraz eğmekten bahsediyoruz, bu derste çok fazla eğme bükme yapmıyoruz [1].

İlk bakacağımız örnek çift entegratör, $\ddot{q} = u$. Bu örnekte herşeyi analitik olarak yapabilirim. Bu denklemin fiziksel karşılığını düşünmek istersek, buz üzerinde duran birim kütlede bir tuğla düşünebiliriz. Tuğlaya uygulanan kontrol kuvveti $F = u$, sürtünme yok.

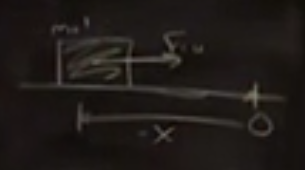
[Dikkat hem kordinat üzerinde hem de konumsal değişken olarak $x$ kullanılmış, karışıklık olmasın]

Bu çift entegratör ile yapmak istediğimiz onu orijin noktasına ve sıfır hıza getirmek. Bariz olmayabilir ama bunu yapmanın pek çok yolu var ve bizim amacımız bu işi yaparken bir tür optimallik kriterine uyarak onu yapmak. Derslerimizin geri kalan tümünde optimallik kriteri bizim için bir tür hesapsal baston görevini görecek.

İlk önce kutup yerleştirme (pole placement) analiziyle başlamak istiyorum. Sistemi durum uzay (state space) formatında yazalım. Durum için çoğunlukla $x$, kordinat için $q$ kullanılır, altta solda görülüyor. Altta sağda durum uzay dinamiğidir, genel bir sistemi tarif ediyor,

$$ x = \left[\begin{array}{c} q \\ \dot{q} \end{array}\right] \quad \dot{x} = A x + Bu $$

O zaman üstteki en basit sistemi tarif etmek için

$$ \dot{x} = \left[\begin{array}{rr} 0 & 1 \\ 0 & 0 \end{array}\right] x + \left[\begin{array}{c} 0 \\ 1 \end{array}\right] u $$

Verili $A,B$ ile açılımı yapınca çift entegratör sistemini elde ettiğimizi göreceğiz.

Amacımız $u$'yu bulmak, tuğla üzerinde etki eden öyle bir kontrol eylemi $u = \pi(x)$ bulalım ki sistemi sıfır noktasına getirsin. Yani amacımız bir geri besleme kanunu $\pi$ bulmak ($\pi$ sembolünü $x$'in fonksiyonu olan kontrol ilkeleri için kullanıyorum). Şu formdaki $u$'lar ile başlayabiliriz; $u = -K x$. Görülen $K$ bir matris, $x$ alınıyor ve $-K$ ile ölçekleniyor. Bu örnekte $K$ matrisi $1 \times 2$ boyutunda, $\left[\begin{array}{cc} k_1 & k_2 \end{array}\right]$,

$$ -K x = \left[\begin{array}{cc} k_1 & k_2 \end{array}\right] \cdot \left[\begin{array}{cc} q \\ \dot{q} \end{array}\right] = -k_1 q - k_2 \dot{q} $$

Bazılarımız bir formu orantılı türevsel kontrolör olarak tanıyacaktır.

Şimdi $K$'yi değiştirince sistemime ne olacak diye düşünüyorum, bu hesap lineer sistemlerde kolay, $u = -Kx$'i denkleme geri sokarsam

$$ \dot{x} = (A - BK)x = \left[\begin{array}{rr} 0 & 1 \\ -k_1 & -k_2 \end{array}\right] x $$

elde ederim. Diferansiyel denklemler dersi alanlar üstteki denklemi nasıl çözeceğimizi bilir, çözüm sistemin özdeğerlerini kullanır, üstteki matrisin özdeğerlerini hesaplarız, sonra özvektörler $v_1,v_2$'yi buluruz,

$$ \lambda_{1,2} = \frac{-k_2 \pm \sqrt{k_2^2 - 4 k_1}}{2}, \quad v_1 = \left[\begin{array}{r} 1 \\ \lambda_1 \end{array}\right], \quad v_2 = \left[\begin{array}{r} 1 \\ \lambda_2 \end{array}\right] $$

Peki sistemin stabil olması için özdeğelerin belli değerlerde olması gerekiyor değil mi? İkisinin de negatif olması. Sistemde salınım olup olmadığını merak ediyoruz, bu durum kompleks özdeğerler varsa olur, ki bu durum üstteki karekök içinde eksi değer varsa ortaya çıkar, onun olması için de $4 k_1$ değeri $k_2^2$ olmalı.

Biz salınım istemiyoruz, $4 k_1 > k_2^2$, bu durumda sistem aşırı sönümlu, $4 k_1 = k_2^2$ ise kritik sönümlu, $4 k_1 < k_2^2$ ise eksik sönümlu, ayrıca stabilite için $\lambda_{1,2} < 0$ olmalı.

Bu sonuçları faz grafiklerine bağlayalım; özdeğer ayrıştırması yapmamızın bir diğer sebebi sistemi çok güzel grafiksel şekilde yorumlamamıza izin vermesi. Spesifik bir duruma bakalım, $k_1 = 1$, ve aşırı sönümlu bir sistem için $k_2$ en az 2 olmalı, onu $k_2 = 4$ yapayım. Özdeğerler bu durumda

$$ \lambda_{1,2} = \frac{-4 \pm \sqrt{16-4}}{2} = -2 \pm 3 $$

$$ \lambda_1 = 0.25, \lambda_2 = -3.75 $$

Şimdi durum uzay grafiğini çizebilirim, $q,\dot{q}$ kordinat sisteminde, ilk önce $-0.25$ eğiminde $v_1$ bir çizgisi çizerim, sonra kabaca $-4$ eğiminde bir çizgi daha çizerim, $v_2$. Sonumlu sistemdeyiz, bu yüzden çizgilerdeki oklar dışarıdan içeri doğru.

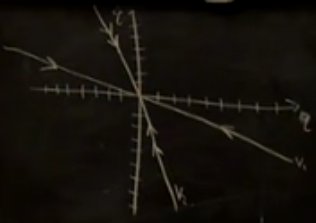
Bu arada anlatım açısından, ve birkaç tane grafik çizmemek için aşırı sönümlü sistem seçtim, böylece tekrarlanan özdeğer çıkmadı, yani salınım olmadı. Ama aşırı sönümlü sistem konuyu irdelemek için yine de iyi çünkü tekrarlanan özdeğer olmayınca özvektörler uzayı kapsar (span). Ya da, her başlangıç konumu iki özvektörün lineer kombinasyonu olarak yazılabilir.

$$ x(0) = \alpha_1 v_1 + \alpha_2 v_2 $$

gibi, ki $\alpha_{1,2}$ bir kombinasyonu oluşturacak herhangi iki sabit. Nihai sistem ise

$$ x(t) = \alpha_1 e^{\lambda_1 t}v_1 + \alpha_1 e^{\lambda_2 t} v_2 $$

Lineer sistemlerin güzel tarafı bu. Bu demektir ki özvektörleri grafiklediğim zaman sistemın tüm faz grafiğini biliyorum. Mesela altta görülen başlangıçtan $v_2$ çok hızlı, $v_1$ biraz daha az hızda bizi sıfıra götürecek, bu ikisinin birleşimi sonucunda alttaki gibi bir gidiş yolu takip edilecektir.

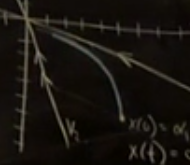
Kontrol konusuna gelelim. $k_1,k_2$'yi değiştirebiliyoruz, ve bu parametreleri değiştirmek demek faz portresini değiştirmek demektir değil mi? Onları öyle değiştirmeliyim ki sistem istediğim şeyi yapsın. Bu değişimi, o değişimi yaratacak $k$'leri nasıl ortaya çıkartmalıyım. Optimalliğe girmeden önce mesela $k_2^2$ $4k_1$'ten büyük olduğu sürece salınıma girmeyeceğimi biliyorum, bu iyi. O zaman niye $k_{1,2}$'yi sonsuza çıkartmıyorum, hemen kut diye sonuç ulasayım? Bu başka problemler çıkartabilir, biriniz fazla enerji diyor, doğru. $k_{1,2}$ olmasa ne olurdu? O zaman $\dot{x} = Ax$ kalır sadece bu sistem sadece direk grafikte sağa doğru gider.

Biz bu basit sistemde optimal geri beslemeli kontrol hesaplayacağız.

Katı bir kısıtlama ekleyelim, $|u| < 1$, $u$'nun mutlak değeri 1'den küçük olsun. Bu pek çok şeyi değiştirir, biraz önceki lineer sistem analizim ise yaramaz hale gelir mesela. Formülize ederken

$$ u = sat(-Kx) $$

diyebilirim, $sat$ ifadesi İngilizce satüration'dan (doygunluk) geliyor, -1 altı için -1, +1 üstü için +1 yapıyorum. Üstte görülen gidiş yolları hala hafiften geçerli, hala orijine gideriz, ama yol biraz daha uzayabilir çünkü kut diye inebilmek yerine daha ufak artışlarla gitmek zorundayız, ve hala stabilliği kaybetmiyoruz. Ama katı kısıtlılıkları iyi ayarlamam gerekiyor ki yol da çok uzamasın.

Bu ayarı yapmanın bir yolu optimal kontrol ile. Tek yolu değil muhakkak, bir yolu. Diyelim ki hayattaki tek amaçım orijine gidebileceğim en hızlı şekilde gitmek, ama $|u| \le 1$ kısıtlamasına tabiyim. Bu aslında ünlü minimum zaman problemi,

$\left[\begin{array}{cc} 0 & 0 \end{array}\right]^T$'a gidebildiğin kadar çabuk git $|u| \le 1$ kısıtlamasına tabi olarak. Tabii hem $q=0$ hem de $\dot{q}=0$, yani hız da sıfır olacak. Orijin derken yer ve hızdan oluşan kordinat sistemindeki "orijinden" bahsediyoruz.

Soruya teorik olarak daha dalınca bu sorunun iyi şekillenmiş olması için kısıtlamanın olması gerektiğini de görürdük, yoksa, daha önce dediğim gibi, sonsuz büyüklükte $u$ kullanabilirdim, sonsuz hızda ulaşırdım ve birşey öğrenmemiş olurdum.

Şimdi buz üzerinde tuğla hakkında zihnimizdeki tüm hayal gücü, bilgi kırıntısını kullanalım. Eğer sınırlı bir kuvvet uygulayabiliyorsam, ve orijine en çabuk şekilde ulaşmak istiyorsam, ne yapmalıyım? Biriniz çat-çat (bang-bang) dedi. Doğru. İleride bir yere mümkün olduğu kadar çabuk ulaşmak istiyorsam çat diye gaza basarım hızlanabildiğim kadar hızlanırım, sonra belli bir kritik noktada çat diye frene başarım ve yavaşlamaya başlarım ve kaya kaya hedef noktasına geleceğim. Bundan daha iyisi mümkün değil. Bunu ispatlayacağız tabii. Bu cevabı çift entegratör olarak kafadan düşünebilirdik, ama yürüyen bir robot için o kadar kolay düşünülemeyebilir, ve biz cevabı genel bir altyapı üzerinden türetmeye uğraşacağız.

Bazen bazılarının "çat-çat kontrol optimaldir" dediğini duyabilirsiniz, bu sonuç yapıcılarınız (actuator) üzerinde katı sınırlar olduğu zaman sıkça ortaya çıkar, ve bu sınırlar olduğu zaman o sınırlara en yakın şekilde davranmak her zaman daha iyidir (o yüzden cat diye hızlanmak gerekli). Robotlarda bu yaklaşım her zaman işlemiyor, çünkü tek bir zaman aralığında yapıcıya maksimum kuvvet, sonra maksimum negatif kuvvet o durumda iyi olmuyor.

İşin püf noktası herhalde çat diye gaza bastıktan sonra ne zaman frene geçeceğimizi bulmak değil mi? Önce onu bulmaya uğraşalım, ortaya çıktığı sistem durumları herhalde birkaç tanedir. O durumları bulmaya çalışalım. $q>0$ durumuna bakalım önce, bir bölüm seçelim, bu durumda fren $u=1$ değil mi (gidiş orijine doğru ise fren onun tersi yönde, yani pozitif yönde olmalı)? O zaman alttaki formülü entegre edelim,

$$ \ddot{q}(t) = u = 1 $$

$$ \dot{q}(t) = u t + \dot{q}(0) \qquad (1) $$

Bir daha entegre

$$ q(t) = q(0) + \dot{q}(0) t + \frac{1}{2} u t^2 \qquad (2) $$

Formüle bakalım ve $u=1$ ile bizi bir nihai $t$'de $q(t)=0$ ve $\dot{q}(t)=0$ götürecek hangi gidiş yollarının ortaya çıktığına bakalım.

$\dot{q}(t)=0$ formülünü (1)'e sokarsak,

$$ \dot{q}(0) = - u t \qquad (3) $$

Üstteki formülü (2)'ye sokarsak, ve $q(t)=0$ olduğu için (2) formülü

$$ q(0) = \frac{1}{2} ut^2 \qquad (4) $$

$t$ için çözelim, $u=1$ demiştik, o zaman (3)

$$ t = -\dot{q}(0) $$

olur. Ve üsttekini (4)'e koyarsak, ve yine $u=1$ ile

$$ q(0) = \frac{1}{2} \dot{q}(0)^2 $$

Bu sonucu konum uzayında grafiklersem bir sonuçlar manifoldu elde edeceğim.

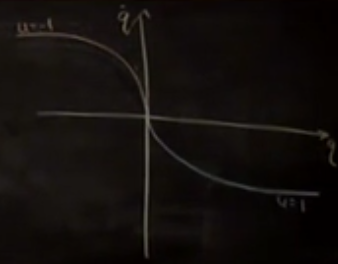
Sağ üst köşe niye boş, orada zaman eksi olmalı ama negatif zamana izin yok. Sağ alt köşede bir sürü çözümlerin oluşturduğu bir çizgi görüyoruz. Diyelim çizginin sonunda frene basıyoruz, ve çizgi boyunca yavaşlayıp yavaşlayıp orijine eriseceğiz (durmuş olacağız). $-q$ durumu için sol üstteki grafiği elde ediyoruz, orada $u=-1$.

Peki eğer karalanan yerlerden birinde isem mesela yeşil noktada ne yaparım? Gösterilen manifold fren yapmanın grafiği. Önce hızlanırım sonra fren yaparım demiştim değil mi? O zaman yeşil noktadaysam yukarı çıkarım ve grafiğe gelirim ve oradan frenler orijine erişirim.

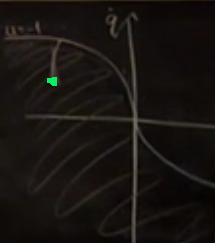
Eğer çizginin üstteki başlıyorsam? O zaman manifolda paralel bir şekilde aşağı inerim, ve yukarı doğru ufak bir gidiş yaparım.

Göstermesi daha zor olan bunları yapmanın optimal olduğunu ispatlamak. Optimallik konusu diger derslerde islenecek.

Çift Entegre Edici ve Hamiltonian Çözüm

Cift-entegre edici (double-integrator) problemine farkli bir sekilde bakalim [3, sf. 519], [2, sf. 308], [4, sf. 250]. Bu problemde amac tek eksen üzerinde $y$ diyelim, bir objeyi bir konumdan diğerine hareket ettirmekti.

Ana fizik formülleri $F = ma$'dan hareketle,

$$ m \ddot{y} = f(t) $$

olabilir, hız $\dot{y}(t)$, ivme $\ddot{y}(t)$, konum $y(t)$. Eğer

$$ x_1(t) = y(t), \quad x_2(t) = \dot{y}(t) $$

dersek ODE sistemini şu şekilde tanımlayabiliriz,

$$ \dot{x}_1(t) = x_2(t) $$

$$ \dot{x}_2(t) = u(t) $$

ki $u(t) = f(t)/m$ olacak. O zaman sistem formulu

$$ \dot{x} = f(x) = \left[\begin{array}{r} x_2(t) \\ u(t) \end{array}\right] $$

Şimdi bir optimal zaman problemi soralım, ve bir kısıtlama yaratalım.

Kontrol $|u(t)| < 1, \forall t \in [t_0,t_f]$ olmalı. Bu objeyi herhangi bir $[x_1(0),x_2(0)]$ başlangıcından orijine minimal zamanda götürmek için kullanılacak optimal kontrol nasıl hesaplanır?

Zaman optimize edildiği için, $V = 1$ kabul ederiz çünkü onun üzerinden alınan entegral zamanı optimize etmeye çalışacaktır,

$$ J = \int_{t_0}^{t_f} V \mathrm{d} t = \int_{t_0}^{t_f} 1 \mathrm{d} t = t_f - t_0 $$

Hamiltonian şöyle oluşturulur,

$$ \mathcal{H}(x,\lambda,u) = V + \lambda^T f $$

$$ = 1 + \lambda_1 x_2 + \lambda_2 u $$

Elimizde lineer ve içbükey bedelli sistem var, bu sistemler için optimalliğin yeterli şartı $0 = \left( \frac{\partial \mathcal{H}}{\partial u} \right)$, optimallik noktasında elde edilen $u^\ast$ için

$$ \mathcal{H}(x^\ast,\lambda^\ast,u^\ast) \le \mathcal{H}(x^\ast, \lambda^\ast, u) $$

$$ = \min_{|u|<1} \mathcal{H}(x^\ast, \lambda^\ast, u) $$

doğru anlamına gelir. Problemimiz icin

$$ 1 + \lambda_1^\ast x_2^\ast + 1 + \lambda_2^\ast u^\ast \le 1 + \lambda_1^\ast x_2^\ast + 1 + \lambda_2^\ast u $$

ki bu da

$$ \lambda_2^\ast u^\ast \le \lambda_2^\ast u $$

demektir. Bu şartı tatmin eden optimal kontrol $u^\ast$ ne olabilir? Eğer $\lambda_2^\ast$ pozitif ise $u^\ast$ mümkün olan en büyük negatif değere sahip olmalıdır ki üstteki küçüklük şartı her zaman geçerli olsun, yani $-1$. Eğer $\lambda_2^\ast$ negatif ise $u^\ast$ mümkün olan pozitif değerde kalmalıdır, yani $+1$. Bu değerleri en basit şekilde

$$ u^\ast(t) = -sgn(\lambda_2^\ast (t)) $$

ile özetleyebiliriz, ki $sgn$ fonksiyonu işaret (sign) fonksiyonu, bir sayının sadece işaretini verir, yani -, + anlaminda, ya da -1, +1. Mesela 3,4 gibi değerler için +1 döndürür, -3,-4 gibi değerler için -1 döndürür.

Kontrolün $\lambda_2^\ast$'ya bağlı olduğu görülüyor, o zaman $\lambda_2^\ast$'yi bulmak için, eskonum denklemlerini kullanarız,

$$ \dot{\lambda}_1 ^\ast(t) = \frac{\partial \mathcal{H}}{\partial x_1^\ast} = 0 $$

$$ \dot{\lambda}_2 ^\ast(t) = \frac{\partial \mathcal{H}}{\partial x_2^\ast} = -\lambda_1^\ast(t) $$

Üstteki denklemleri entegre edersek, mesela $\dot{\lambda}_1 ^\ast(t)=0$ ile başlayalım,

$$ \lambda_1^\ast(t) = \lambda_1^\ast(0) $$

Değil mi? Sıfırı entegre edince bir sabit elde edilir, bu sabit $\lambda_1^\ast(t)$'nin başlangıç değeri $\lambda_1^\ast(0)$. İkinci entegrasyon $\dot{\lambda}_2 ^\ast(t) $ için, bu değişken $-\lambda_1^\ast(t)$'a eşit, biraz önce bu değeri bulduk, onu yerine koyup entegre edince,

$$ \lambda_2^\ast(t) = \lambda_2^\ast(0) - \lambda_1(0) t $$

$u^\ast(t)$'nun bağlı olduğu $\lambda_2^\ast (t)$ ortaya çıktı, bu bir düz çizgiyi gösteriyor. Bir düz çizgi ya eksiden artıya, ya artıdan eksiye, ya da ekside, artıda kalacağı için (başka seçenek yok), optimal kontrol seçenekleri [-1], [+1], [+1,-1], [-1,+1] olabilir.

Çözümde daha da ilerleyince [3, sf. 519] sonuç olarak $x_1,x_2$ grafiğinde paraboller ortaya çıkar.

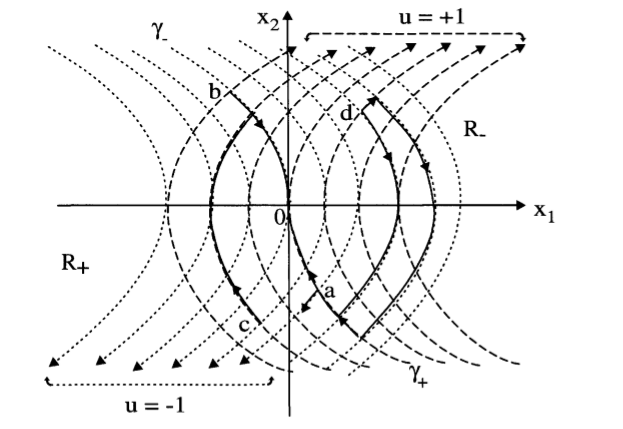
Bu grafikte -1 aşağı giden gidiş yollarını +1 yukarı giden gidiş yollarını temsil eder. Eğer bir başlangıç noktası, mesela $d$'den orijine gitmek istiyorsak, önce -1 ile aşağı ineriz, sonra +1 ile $a$'dan geçen yukarı yolla kesiştiğimiz yerde o gidiş yoluna değişim yaparız ve orijine ulaşırız.

Kaynaklar

[1] Tedrake, MIT, 6.832 Underactuated Robotics, Ders 1, https://youtu.be/Z8oMbOj9IWM

[2] Athans, Optimal Control An Introduction to the Theory and Its Applications

[3] Naidu, Optimal Control Systems

[4] Kirk, Optimal Control Theory An Introduction