Değişimsel Calculus (Calculus of Variations) ve Euler-Lagrange Denklemi

İki nokta arasındaki en kısa mesafe hangisidir? Bu basit soru belki bizi güldürmüştür çünkü cevabı çok iyi biliyoruz. Ama bu cevabı ispatlayabilir miyiz? Birazdan bunu yapacağız.

Ama birazdan işleyeceğimiz tekniklerin faydasını daha iyi belirtmek için örneklere devam edelim; Dünya üzerindeki iki nokta arasındaki en kısa yüzeysel mesafe sorulsa bunun bir çembersel bir yol olacağını biliriz. Ama ya aynı soruyu mesela bir elipsoid ya da bir silindir ya da bir koni yüzeyi için sorsak? Herhangi bir yüzey üzerinde iki nokta arası en kısa mesafe soruları için değişimsel calculus kullanılabilir.

DC ile minimum problemlerini çözmüş oluruz bir bakıma, aynen $f(x)$'in minimum'unu bulmak için $f'(x) = 0$ yapıp işleme devam etmek gibi. Fakat DC ile pek çok farklı fonksiyon arasından istediğimiz sonucu minimize eden özgün fonksiyonu bulmaya uğraşıyoruz, tek bir fonksiyonun tek minimum noktasını değil. Bu sebeple DC daha geniş problemler için kullanılabilir.

Örnek

Bir düzlem üzerindeki $x_1,y_2$ ile $x_2,y_2$ noktasını birleştiren en kısa $y(x)$ eğrisini bulun.

Cevap

Doğru cevap tabii ki düz bir çizgi. Ama bunu bilmiyormuş gibi yapalım.

Minimize etmek istediğimiz

$$ I = \int_{x_1}^{x_2} \sqrt{ 1 + y'^2} \mathrm{d} x $$

Yani eğri uzunluğu. Üstteki formülün nereden geldiğini [5]'te görebiliriz. İfadenin söylediği bulmak istediğimiz $y$ için öyle bir $y = y(x)$ "ekstremsel (extremal) değer" bulmak ki $I$ en kısa olsun. Şimdi bize aynı başlangıç, bitiş noktalarından geçen ama (hala bilinmeyen) ekstremselden biraz farklılaşan tüm eğrileri cebirsel olarak temsil etmenin bir yolu gerekli.

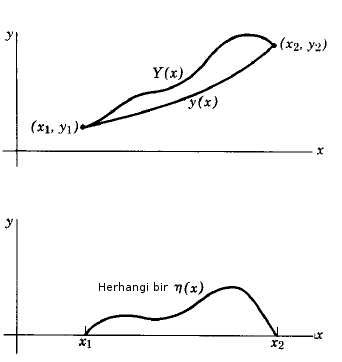
Bu farklı eğrileri şöyle temsil ediyoruz; diyelim ki $\eta(x)$ herhangi bir fonksiyon olsun, bu fonksiyon $x_1$ ve $x_2$ noktalarında sıfır olmalı, sürekli bir ikinci türevi var. Ama bunun haricinde $\eta$ herhangi bir şey olabilir. Şimdi bir $Y(x)$ tanımlıyoruz,

$$ Y(x) = y(x) + \epsilon \eta(x) \qquad (3) $$

ki $\epsilon$ bir parametre. $\eta(x)$ herhangi bir şey olabileceği için $Y(x)$ fonksiyonu da $(x_1,y_2),(x_2,y_2)$ noktalarindan geçen herhangi bir eğri olabilir. Biz tüm bu eğriler içinden

$$ I = \int_{x_1}^{x_2} \sqrt{ 1 + Y'^2} \mathrm{d} x \qquad (2) $$

formülünü minimal yapanı istiyoruz. Üstteki tanım sayesinde $I$ fonksiyonu $\epsilon$'un fonksiyonu haline geldi. $\epsilon = 0$, ve $Y = y(x)$ değerleriyle ekstremsel değeri elde ediyoruz. Şimdi istediğimiz $\epsilon=0$ iken $I(\epsilon)$'un minimum değerini almasını sağlamak. Diğer bir deyişle

$$ \epsilon = 0 \quad \textrm{için} \quad \frac{\mathrm{d} I}{\mathrm{d} \epsilon} = 0 $$

olmasını istiyoruz.

(2)'nin $\epsilon$'a göre türevini alalım,

$$ \frac{\mathrm{d} I}{\mathrm{d} \epsilon} = \int_{x_1}^{x_2} \frac{1}{2} \frac{1}{\sqrt{1 + Y'^2}} 2Y' \left( \frac{\mathrm{d} Y'}{\mathrm{d} \epsilon} \right) \mathrm{d} x $$

Üstteki formüldeki $Y'$ değerini bulmak için (3)'un $x$'e göre türevi

$$ Y'(x) = y'(x) + \epsilon \eta'(x) \qquad (4) $$

Şimdi üsttekinin $\epsilon$'a göre türevi alınabilir,

$$ \frac{\mathrm{d} Y'}{\mathrm{d} \epsilon} = \eta'(x) $$

Tüm bunları üç üstteki formüle geri koyarsak,

$$ \left( \frac{\mathrm{d} I}{\mathrm{d} \epsilon} \right)_{\epsilon = 0} = \int_{x_1}^{x_2} \frac{ y'(x)\eta'(x) }{\sqrt{1 + y'^2}} \mathrm{d} x = 0 $$

Parcali entegrasyon uygulayabiliriz (cunku $\eta$ ve $y$'nin surekli ikinci turevinin oldugunu farz etmistik zaten),

$$ u = y' / \sqrt{1 + y'^2}, \quad \mathrm{d} v = \eta'(x) \mathrm{d} x $$

O zaman

$$ \mathrm{d} u = \frac{\mathrm{d}}{\mathrm{d} x} \left( \frac{y'}{\sqrt{1+y'^2}} \mathrm{d} x \right), \quad v = \eta(x) $$

Yani

$$ \left( \frac{\mathrm{d} I}{\mathrm{d} \epsilon} \right)_{\epsilon = 0} = \frac{y'}{\sqrt{1+y'^2}} \eta(x) \bigg\vert_{x_1}^{x_2} - \int_{x_1}^{x_2} \eta(x) \frac{\mathrm{d}}{\mathrm{d} x} \left( \frac{y'}{\sqrt{1+y'^2}} \right) \mathrm{d} x $$

Üstteki ifadede ilk terim sıfır olacaktır çünkü $\eta(x)$ üç noktalarında sıfırdır. Geriye kalanların sıfır sonucunu vermesi için

$$ \frac{\mathrm{d}}{\mathrm{d} x} \left( \frac{y'}{\sqrt{1+y'^2}} \right) = 0 $$

olmalıdır, yoksa, eğer bu ifade sıfır değilse herhangi bir $\eta(x)$ seçilebilirdi ve bu $\eta$ sıfır olma ihtimalini ortadan kaldırırdı. Nüansa dikkat; diyoruz ki iki üstteki entegralin her zaman, her $\eta$ için sıfır olmasının tek yolu üstteki ifadenin doğru (sıfır) olması.

Devam edersek üstteki formülü $x$'e göre entegre edersek,

$$ \int \frac{\mathrm{d}}{\mathrm{d} x} \left( \frac{y'}{\sqrt{1+y'^2}} \right) \mathrm{d} x = \int 0 \mathrm{d} x $$

$$ \left( \frac{y'}{\sqrt{1+y'^2}} \right) = \textrm{ sabit } $$

Mantığa devam edelim, üstteki sabitlik $y'$ değerinin sabit olması demektir.

Demek ki $y$'nin eğimi sabit, eğimi sabit olan şey nedir? Bir düz çizgi!

Oldukça iş yaptıktan sonra bir sonuca eriştik. Bu tür işlemleri her tür problem için arka arkaya tekrarlayabilirdik, ama genel bir problem şablonu için bu çözümü yapmak ve bir şablon sonuca erişmek çok daha rahattır, böylece o şablon sonucu ardı ardına her yeni problemde kullanabiliriz, tek gereken şablondaki değişkenlerin ne olduğuna bakmaktır, ve şablondan direk sonucu alabiliriz.

Amac

$$ I = \int_{x_1}^{x_2} F(x,y,y') \mathrm{d} x $$

entegralini durağan (stationary) yapacak $y$ fonksiyonunu bulmak, ki $F$ bize verilen bir fonksiyon. $I$'yi durağan yapan $y$'ye extremsel deniyor, $I$ maksimum, minimum olsun farketmiyor. Metot biraz önce düz çizgi için kullandığımız metot gibi, bir

$$ Y(x) = y(x) + \epsilon \eta(x) $$

ile pek cok farkli egri dusunmek. Simdi

$$ I = \int_{x_1}^{x_2} F(x,Y,Y') \mathrm{d} x $$

entegraline bakalım ve istediğimiz $\epsilon = 0$ iken $ \mathrm{d} / \mathrm{d} \epsilon) ) I(\epsilon) = 0$ olması. $Y,Y'$ değerlerinin $\epsilon$'un fonksiyonları olduğunu hatırlıyoruz, ve entegralin $\epsilon$'a göre türevini alınca,

$$ \frac{\mathrm{d} I}{\mathrm{d} \epsilon} = \int_{x_1}^{x_2} \left( \frac{\partial F}{\partial Y} \frac{\mathrm{d} Y}{\mathrm{d} \epsilon} + \frac{\partial F}{\partial Y'} \frac{\mathrm{d} Y'}{\mathrm{d} \epsilon} \right) \mathrm{d} x $$

(3) ve (4)'u üstteki formüle sokarsak,

$$ \frac{\mathrm{d} I}{\mathrm{d} \epsilon} = \int_{x_1}^{x_2} \left[ \frac{\partial F}{\partial Y} \eta(x) + \frac{\partial F}{\partial Y'} \eta'(x) \right] \mathrm{d} x $$

$\epsilon = 0$ iken $ \mathrm{d} / \mathrm{d} \epsilon) ) I(\epsilon) = 0$ istiyoruz demiştik, ve hatırlarsak $\epsilon = 0$ demek, $Y = y$ demekti. O zaman üstteki

$$ \left( \frac{\mathrm{d} I}{\mathrm{d} \epsilon} \right)_{\epsilon = 0} = \int_{x_1}^{x_2} \left[ \frac{\partial F}{\partial y} \eta(x) + \frac{\partial F}{\partial y'} \eta'(x) \right] \mathrm{d} x = 0 $$

olur. $y"$ değerinin sürekli olduğunu farzederek, üstteki ikinci terimi aynen biraz önceki problemde olduğu gibi parçalı entegralle açmaya uğraşacağız,

$$ \int_{x_1}^{x_2} \frac{\partial F}{\partial y'} \eta'(x) \mathrm{d} x = \frac{\partial F}{\partial y'} \eta(x) \bigg\vert_{x_1}^{x_2} - \int_{x_1}^{x_2} \frac{\mathrm{d} }{\mathrm{d} x} \left( \frac{\partial F}{\partial y'} \right) \eta(x) \mathrm{d} x $$

Entegre edilmiş kısım sıfır çünkü önceki gibi $\eta(x)$ üç noktalarında sıfır, o zaman

$$ \left( \frac{\mathrm{d} I}{\mathrm{d} \epsilon} \right)_{\epsilon = 0} = \int_{x_1}^{x_2} \left[ \frac{\partial F}{\partial y} - \frac{\mathrm{d} }{\mathrm{d} x} \frac{\partial F}{\partial y'} \right] \eta(x) \mathrm{d} x = 0 $$

Yine biraz önceki gibi, $\eta$ herhangi bir fonksiyon olabileceği için,

$$ \frac{\partial F}{\partial y} - \frac{\mathrm{d} }{\mathrm{d} x} \frac{\partial F}{\partial y'} = 0 $$

olmalıdır. Üstteki formüle Euler denklemi ismi verilir.

O zaman değişimsel Calculus'taki pek çok problem durağan olması istenen bir entegral oluşturmak, $F$'in ne olduğunu ayarlamak, ve değişkenleri, fonksiyonları üstteki Euler denklemine sokmak ve elde edilen (çok daha basit) diferansiyel denklemi çözmektir.

Örnek

Başta gördüğümüz düzlem üzerindeki en kısa mesafe problemini yeni genel metotumuz ile çözelim. Minimize etmek istediğimiz

$$ \int_{x_1}^{x_2} \sqrt{1 + y'^2} \mathrm{d} x $$

Yani $F = \sqrt{1 + {y'}^2}$. O zaman,

$$ \frac{\partial F}{\partial y'} = \frac{y'}{\sqrt{1 + y'^2}}, \quad \frac{\partial F}{\partial y} = 0 $$

Euler denklemine danışarak, $F,y,x$'leri yerine koyup,

$$ \frac{\mathrm{d}}{\mathrm{d} x} \left( \frac{y'}{\sqrt{1 + y'^2}} \right) = 0 $$

elde ediyoruz. Bu biraz önce elde ettiğimiz sonuç ile aynı.

Birden Fazla Değişken

Kendimizi tek bir bağımlı değişken $y$ ile sınırlamamıza gerek yok; temel Calculus'tan hatırlarsak $z = z(x)$'te bir minimum nokta olması için gerekli şart $\mathrm{d} z / \mathrm{d} x = 0$. İki değişkenli bir $z = z(x,y)$ için gerekli iki şart var, $\partial z / \partial y = 0$ ve $\partial z / \partial x = 0$.

Diyelim ki bize bir $F$ verildi ve bu $F$, $y$, $z$, $\mathrm{d} y / \mathrm{d} x$, $\mathrm{d} z / \mathrm{d} x$, ve $x$'in bir fonksiyonu ve bulmak istediğimiz iki tane eğri, $y=y(x)$ ve $z=z(x)$ öyle ki bu eğriler $I = \int F \mathrm{d} x$ entegralini durağan hale getiriyor. O zaman entegralin değeri hem $y(x)$ hem de $z(x)$'e bağımlı olur ve tahmin edebileceğimiz gibi bu durumda iki tane Euler denklemi gerekir, bir tane $y$ bir tane $z$ için, yani

$$ \frac{\mathrm{d}}{\mathrm{d} x} \left( \frac{\partial F}{\partial y'} \right) - \frac{\partial F}{\partial y} = 0 $$

$$ \frac{\mathrm{d}}{\mathrm{d} x} \left( \frac{\partial F}{\partial z'} \right) - \frac{\partial F}{\partial z} = 0 $$

Biraz önce tek değişkende gösterilen teknikleri kullanarak üsttekinin doğru olduğunu ispatlayabiliriz.

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

Alternatif Anlatım

Değişimsel, Varyasyonel Calculus bir fonksiyonelin (dikkat "fonksiyon" değil) ekstrema (minimum / maksimum) ya da durağan (stationary) olduğu noktaların bulunması için kullanılır.

Bir fonksiyonel bir veya daha fazla fonksiyonun birleşimidir. Fonksiyonel girdi olarak bir fonksiyon alıp sonuç olarak bir sayısal değer hesaplayan bir ikinci fonksiyondur aslında. Diğer bir tanım fonksiyonelin belli fonksiyon "tipleri", "sınıfları" için bir sayısal değer ataması yaptığıdır.

Değimsel Calculus'un en temel, bilinen, standart problemi, sabit $x$ değerleri için alttaki fonksiyonelin (entegralin) durağan olduğu $\phi(x)$ fonksiyonlarını bulmaktır. Yine dikkat: Bulmaya çalıştığımız bir skalar $x$ değeri değil, bir veya daha fazla fonksiyondur.

$$ I(\phi)=\int_a^b F(x,\phi,\phi_x) \mathrm{d} x $$

$\delta$ işareti varyasyon operatörüdür, ve diferansiyel operatörü $d$'ye oldukça benzer. $\phi(x)$'nin varyasyon operatörü uygulanmış hali olan $\delta \phi(x)$'in tanımı, sabit bir $x$ değeri için herhangi (arbitrary), sonsuz ufaklıkta (infinitesimal) bir değişim demektir. Doğal olarak $x$'in sabit olması $\delta x = 0$ anlamına gelir (bu eşitliği birazdan formülümüzün açılımında basitleştirme amacı ile kullanacağız). Fonksiyonelin durağanlığı da $\delta I = 0$ demektir.

Değişimsel Calculus ve Euler-Lagrange açılımının püf noktası altta birazdan göreceğimiz cebirsel işlemlerle, $\delta \phi$'yi formülde tek başına bırakarak bir anlamda durağanlık mantığının dışına atmasıdır. Öyle bir $\phi(x)$ buluyoruz ki ondan $\delta$ sapmaları var, ama biz oraya değil, formülün geri kalanına bakıyoruz, formülün o tarafında üstünde sapmalar olmayan $\phi$ ile işlemler yapacağız, ve optimal bir $\phi$ fonksiyonu bulacağız.

$I$ fonksiyoneli pek çok fizik, diğer tür problemlerde ortaya çıkan bir formdur. Minimize edilmeye uğraşılan bir fonksiyonel var ise, değişimsel calculus burada devreye girebilir, durağan nokta üzerinden optimal bir $\phi(x)$ sonucunu verir.

Türetmeye başlayalım:

$\delta$ operasyonu diferansiyel ve entegral ortamlarında sırabağımsız (commutative) özelliklere sahiptir, bu operasyonların içine "nüfuz edebilir". Mesela

$$ \delta \bigg( \int F \mathrm{d} x \bigg) = \int (\delta F) \mathrm{d} x $$

ve

$$ \delta \bigg( \frac{d\phi}{dx} \bigg) = \frac{d}{dx}(\delta \phi) $$

Üstte bahsettiğimiz fonksiyonelin varyasyonu o zaman

$$ \delta I = \delta \int_a^b F(x,\phi,\phi_x)\mathrm{d} x = 0 $$

$$ = \int_a^b \delta F \mathrm{d} x $$

Şimdi $\delta F$'in açılımını gösterelim. Bu açılım tam diferansiyel (total differential) açılımı ile tıpatıp aynı.

$$ \delta I = \int_{a}^{b} \bigg( \frac{\partial F}{\partial \phi}\delta\phi + \frac{\partial F}{\partial \phi_x}\delta\phi_x + \frac{\partial F}{\partial x}\delta x \bigg) \mathrm{d} x $$

$\delta x = 0$ olduğunu bildiğimize göre bu terimi formülden atabiliriz. Geri kalanlar:

$$ \delta F = \frac{\partial F}{\partial \phi}\delta\phi + \frac{\partial F}{\partial \phi_x}\delta\phi_x
$$

Bunları $\delta I$ formülünün içine koyarsak:

$$ \delta I = \int_{a}^{b} ( \frac{\partial F}{\partial \phi}\delta\phi + \frac{\partial F}{\partial \phi_x}\delta\phi_x ) \mathrm{d} x = 0 $$

Entegraldeki ikinci terime bakalım: $\delta \phi$ formülünü $\delta \phi_x$ formülü içinden "çekip çıkartacağız". Bunu niye yapıyoruz? Çünkü $\delta \phi$'un herhangi (arbitrary) bir değere sahip olabileceğinden hareketle ek bazı sonuçlara gelmeye çalışacağız, bu da sadece $\delta \phi$'nin tek başına kalmasıyla mümkün olabilir.

$\delta$ operatörünün sırabağımsız olduğunu görmüştük. O zaman

$$ \delta \phi_x = \delta \bigg( \frac{d\phi}{dx} \bigg) = \frac{d}{dx}(\delta \phi) $$

$\delta \phi$'yi diferansiyel operatörünün içine attık. Şimdi parçalayarak entegral alma (integration by parts) tekniğini kullanarak diferansiyel operatöründen de kurtulacağız. Parçalayarak entegral alma bilindiği gibi şöyledir:

$$ \int_a^b u \cdot \mathrm{d} v = u \cdot v - \int_a^b v \cdot \mathrm{d} u $$

Eğer $\delta \phi$'in diferansiyelini $dv$'ye atarsak, o zaman parçalayarak entegral alma tekniği $dv$'yi $v$ yaparken bize istediğimiz sonucu verecektir. O zaman açmak istediğimiz entegrali hatırlayalım ve sırabağımsız işlemi uygulayalım:

$$ \int_{a}^{b} \frac{\partial F}{\partial \phi_x}\delta\phi_x \mathrm{d} x = \int_{a}^{b} \frac{\partial F}{\partial \phi_x} \frac{d}{\mathrm{d} x}(\delta \phi) \mathrm{d} x \qquad (1) $$

Parçalayarak entegral alma tekniği için parçaların ne olduğunu tanımlayalım:

$$ u = \frac{\partial F}{\partial \phi_x} $$

$$ du = d \bigg( \frac{\partial F}{\partial \phi_x} \bigg) $$

$$ dv = \frac{d}{dx}(\delta \phi)dx = d(\delta \phi) $$

$$ v = \delta \phi $$

O zaman (1)'ın açılımı şöyle olacaktır:

$$ \frac{\partial F}{\partial \phi_x} \delta \phi \bigg|_a^b - \int_a^b \delta \phi \cdot \mathrm{d} \bigg( \frac{\partial F}{\partial \phi_x} \bigg) $$

Sağdaki terime $dx$'leri eklersek:

$$ \frac{\partial F}{\partial \phi_x} \delta \phi \bigg|_a^b - \int_a^b \delta \phi \cdot \frac{d}{\mathrm{d} x} \bigg( \frac{\partial F}{\partial \phi_x} \bigg) \mathrm{d} x $$

Görüldüğü gibi $\delta \phi$'in diferansiyelinden tamamen kurtulduk. Şimdi bu sonucu $\delta I$ içindeki ikinci terim yerine koyalım:

$$ \delta I = \int_{a}^{b} \bigg[ \frac{\partial F}{\partial \phi}\delta\phi - \delta \phi \cdot \frac{d}{dx} \bigg( \frac{\partial F}{\partial \phi_x} \bigg) \bigg] \mathrm{d} x - \frac{\partial F}{\partial \phi_x} \delta \phi \bigg|_a^b $$

$\delta \phi$'ları dışarı çıkartalım:

$$ \delta I = \int_{a}^{b} \bigg[ \frac{\partial F}{\partial \phi} - \frac{d}{dx} \bigg( \frac{\partial F}{\partial \phi_x} \bigg) \bigg] \delta\phi \mathrm{d} x - \frac{\partial F}{\partial \phi_x} \delta \phi \bigg|_a^b $$

Bu sonuç üzerinden bazı ek mantık yürütmeye başlayabiliriz. Mesela $\delta \phi$ (belli sınırlar dahilinde olmak şartıyla) herhangi bir değere sahip olabileceği için, o zaman $\delta I$'in sıfır olması demek, $\delta \phi$'in sıfır olması garanti olmadığı için (herhangi bir değer dedik ya) $\delta \phi$'in içinde olduğu çarpımda onun haricindeki değerlerin sıfır olmasını mecbur kılacaktır. Bu demektir ki

$$ \bigg[ \frac{\partial F}{\partial \phi} - \frac{d}{dx} \bigg( \frac{\partial F}{\partial \phi_x} \bigg) \bigg] = 0 $$

olmalıdır. Literatürde bu şarta Euler-Lagrange şartı ismi verilmiştir. Aynı şekilde

$$ \frac{\partial F}{\partial \phi_x} \delta \phi \bigg|_a^b = 0 $$

olmalıdır. Bu demektir ki ya $\delta \phi(a) = \delta \phi(b) = 0$ olacaktır, ki bu şarta geometrik ya da kesinlikle gerekli sınır şartları (geometric or essential boundary condition) denir, ya da

$$ \frac{\partial F(a)}{\partial \phi_x} = \frac{\partial F(b)}{\partial \phi_x} = 0 $$

olacaktır, bu şarta da doğal sınır şartı (natural boundary condition) ismi verilir.

Örnek

Şimdi örnek olarak iki nokta arasındaki en kısa eğrinin düz çizgi fonksiyonu olması gerektiğini bulacağız. $F$ fonksiyonu nedir?

$$ F(x,y,y') = [1+(y')^2]^{1/2} $$

Bu fonksiyonun içinde $y$ olmadığına göre Euler-Lagrange'in $\phi$ (yani $y$) içeren kısmın atabiliriz. Kalanlar:

$$ \bigg[ \frac{d}{dx} \bigg( \frac{\partial F}{\partial y'} \bigg) \bigg] = 0 $$

Parantez içindeki kısmi türevi hesaplayalım

$$ \frac{\partial F}{\partial y'} = \frac{1}{2}[1+(y')^2]^{-1/2}\ 2y = \frac{y'}{[1+(y')^2]^{1/2}} $$

Euler-Lagrange formülüne koyarak iki tarafın entegralini alalım ve $dx$'ten kurtulalım:

$$ \int \bigg[ \frac{d}{dx} \bigg( \frac{y'}{[1+(y')^2]^{1/2}} \bigg) \bigg] \mathrm{d} x = c $$

$$ \frac{y'}{[1+(y')^2]^{1/2}} = c $$

Sıfırın entegrali bir sabit sayı olacaktır, bu sabite $c$ ismini verdik. Şimdi üstteki formülü $y'$ sol tarafta tek başına kalacak şekilde tekrar düzenleyelim:

$$ \frac{y'}{[1+(y')^2]^{1/2}} = c $$

$$ \frac{y'}{\sqrt{[1+(y')^2]}} = c $$

$$ \frac{y'^2}{1+(y')^2} = c^2 $$

$$ \frac{1+(y')^2}{y'^2} = \frac{1}{c^2} $$

$$ 1+\frac{1}{y'^2} = \frac{1}{c^2} $$

$$ \frac{1}{y'^2} = \frac{1}{c^2} - 1 $$

$$ \frac{1}{y'^2} = \frac{1-c^2}{c^2} $$

$$ y' = \sqrt{\frac{c^2}{1-c^2}} = a $$

Sağdaki sonuca bakarsak elimize geçen $c$'lerden oluşan bir işlem öbeğidir, ve bu öbek te doğal olarak yine bir sabit sonucunu verir, bu sabite $a$ ismini verdik. Devam edelim, $y'$, yani türevi bir sabit olan fonksiyon, $y(x)$ şuna benzemez mi?

$$ y(x) = ax + b $$

ki sınır şartları $y(x)=x$ (0 ve 1 değerleri için). Bu formül bildiğimiz gibi bir düz çizginin formülüdür!

Demek ki Değişimsel Calculus kullanarak iki nokta arasındaki en kısa yolun düz çizgi olacağını ispatlamış olduk.

Kaynaklar

[1] Everstine, G. C., Numerical Solutions of Partial Differential Equations

[2] Rao, S. S., The Finite Element Method in Engineering

[3] Thomas, Thomas' Calculus, 11th Edition

[4] Boas, Mathematical Methods in the Physical Sciences, 3e

[5] Bayramlı, Çok Boyutlu Calculus, 6. Ders