Hareketin Katı-Gövde Denklemleri

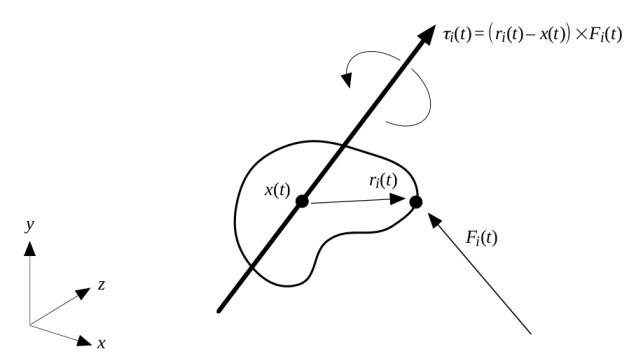
Daha önce rotasyon matrisi bazlı hareket denklemlerini vermiştik. Bu yazıda cisim duruşu ve dönüş mekaniğini kuaterniyon kavramı üzerinden hesaplayacağız, daha önce görülen bazı kavramların da tekrar üzerinden geçeceğiz. Nihai amacımız \(t=0\) anında bir kuvvet uygulanan objenin nasıl davranacağını simüle edebilmek.

Yani momentumun zamansal türevi kuvvettir. Hareket hesaplarında \(F\) entegre edilerek \(p\) hesaplanır, \(p\)’yi \(m\) ile bölerek \(v\) elde ederiz, ve onu entegre ederek cisim yeri \(x\) elde edilir [1, sf. 466].

Lineer momentum kavramı anlaşılması kolay, onu bir tür atalet olarak görüyoruz, hareket eden bir objenin düz bir çizgi üzerindeki hareketini devam ettirmeye olan meyili. Tabii ki bu meyil, hareketin devamlılığı o anki hız ve cismin kütlesiyle orantılı, \(mv\) buradan geliyor. Açısal momentum da benzer bir kavram, tek fark bir eksen etrafında dönmekte olan bir cismin dönmeye devam etme meyili. O zaman üç boyutta, orijin etrafındaki açısal momentum \(\vec{L}\), \(m\) kütleli cismin orijine olan uzaklığı \(\vec{r}\) ile \(m\vec{v}\) çapraz çarpımıdır [1, sf. 42].

Aynen kuvvetin momentumun zamansal türevi olması gibi, tork benzer şekilde açısal momentumun türevidir, bunu görmek için üstteki \(L\)’nin türevini alalım,

\[ \frac{\mathrm{d} L}{\mathrm{d} t} = \frac{\mathrm{d} (r \times p)}{\mathrm{d} t} \]

\[ = r \times \frac{\mathrm{d} p}{\mathrm{d} t} + \frac{\mathrm{d} r}{\mathrm{d} t} \times p \]

\(\mathrm{d} p / \mathrm{d} t = F\), \(\mathrm{d} r / \mathrm{d} t = v\) olduğunu biliyoruz, üstte yerine geçirelim,

Fakat \(v\) ile \(p\) aynı yöne işaret eden vektörler, onların çapraz çarpımı sıfır, geri kalanlar,

Bu formül açısal momentum ile açısal hız \(w\) (diğer kaynaklarda \(\omega\)) ile ilişkilendirir, lineer momentum’daki kütle yerine burada \(J\) (diğer kaynaklarda \(I\) diye geçer) var, ki \(J\) bir atalet tensoru, objenin şekline, ağırlık dağılımına göre değişir, ve bu değerin kendisi de obje döndükçe değişime uğrar.

Hesaplarda gereken uygulanan tork \(\tau(t)\)’un sebep olduğu cisim dönüşünü bulmak, bunun için \(\tau\) entegre edilerek \(L\) elde edilir, \(L\) değeri \(J\) ile bölünerek (daha doğrusu \(J\) bir matris olduğu için onun tersi alıp çarpılarak) \(w\) elde edilir. Kuaterniyon durumunda

entegre edilerek objenin dönüş sonrası yeni işaret ettiği yer bulunur (burada \(\omega\) açısal hızı temsil eden kuaterniyon). Üstteki denklemi türetmek gerekirse [4, sf. 264] kaynağına başvurulabilir. Herhangi iki kuaterniyonun bir geçiş kuaterniyonu ile birbirine bağlanabildiğini biliyoruz. O zaman ufak bir zaman dilimi \(\Delta t\) içinde \(q(t)\) ve \(q(t + \Delta t)\) kuaterniyonlarının nasıl ilişkili olduğuna bakarız, yani aradığımız bir \(\Delta r(t)\) öyle ki

Üstteki formülü kuaterniyon tanımından [3] biliyoruz, dönüş açısı \(2 \Delta \alpha\), ve etrafında dönüşün yapıldığı eksen vektör \(v(t)\).

Dönüş açısı \(\Delta \alpha\) çok ufak, bu sebeple küçük açı yaklaşıklaması [5] üzerinden \(\cos(\Delta \alpha) \approx 1\), \(\sin(\Delta \alpha) \approx \Delta \alpha\), o zaman

\[ \frac{\mathrm{d} q}{\mathrm{d} t} = \lim_{\Delta t \to 0} \frac{q(t + \Delta t) - q(t)}{\Delta t} \]

Dikkat edersek skalar \(\Delta \alpha\) değişimi \(\Delta t\) ile bölünüyor, bu bize skalar açısal değişim \(\omega(t)\)’yı verir. Bu açısal hızın vektör \(v(t)\) ile çarpılması ise \(v(t)\) etrafındaki skalar açısal değişim \(\vec{\omega}(t)\)’yı verir, yani

Son formül dönüş açısı \(2 \Delta \alpha\) içindi, eğer \(\Delta \alpha\) istiyorsak, formülü \(1/2\) ile çarparız. Böylece

formülüne erişmiş olduk. \(q(t)\) için gereken entegrasyon üstteki formül üzerinden yapılır.

Not: Hesapsal hataların birikmemesi için \(q(t)\)’yi sürekli normalize etmek iyi bir fikirdir, bu normalizasyon

Açısal hız: diyelim \(\omega\) radyan/saniye birimli açısal hız, ve kuaterniyon olarak paylaşılmış. Eğer bir zaman dilimi \(\Delta t\) içinde \(\omega\) sabit ise, bu zaman sonrası toplam dönüş \(q'\) ne olurdu? Bu durumda formül,

Hepsini bir araya koyarsak entegrasyonun uygulanacağı nihai yapı şu şekilde gösterilebilir,

\[ \frac{\mathrm{d}}{\mathrm{d} t} \left[\begin{array}{c} x \\ q \\ p \\ L \end{array}\right] = \left[\begin{array}{c} \dot{x} \\ \dot{q} \\ \dot{p} \\ \dot{L} \end{array}\right] = \left[\begin{array}{ccc} m^{-1} p \\ \omega q / 2 \\ F \\ \tau \end{array}\right] \]

Şimdi “sıfırıncı anda’’ yani ilk başlangıçta uygulanan kuvvetleri, lineer, açısal, hesaplamak lazım. Obje üzerinde uygulanan noktaya bildiğimizi farzedelim, sonu o noktada başlangıcı nesne ağırlık merkezinde olan bir vektör ile kuvvet vektörü arasında çapraz çarpım yapıyoruz, bu bize torku veriyor.

Benzer şekilde sonu nesne merkezinde başı o noktada olan bir vektör daha var, lineer kuvvet bu doğrultuda uygulanacak, o vektör üzerine iki üstte görülen kırmızı vektörü yansıtıyoruz, bu da lineer kuvvet oluyor. Bir üstteki resim üzerinde gösterirsek,

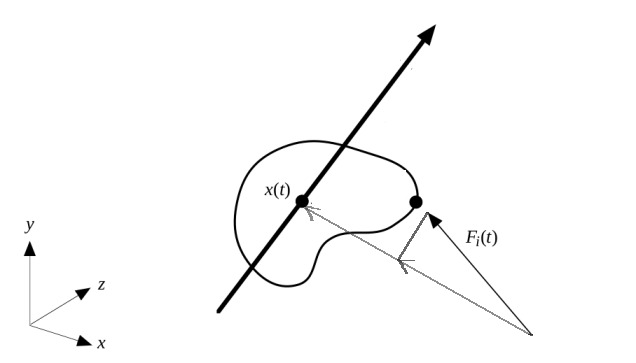
Daha önce söylediğimiz gibi her iki kuvvet de ilk anda lineer ve açısal momentumu ekileyen faktörler, sonraki adımlarda etkileri yok.

Bu kavramların şimdi bir sanal obje üzerinde etkilerini görelim. STL formatında tutulan bir 3D objesi olsun. Uygulanan kuvveti şöyle etki ettiririz, STL objelerinin dışı üçgenlerden oluşur, o üçgenlerden birinin köşesini son nokta olarak alalım, uzayda herhangi bir noktası başlangıç noktası olarak alalım, ve ilk kuvvet bu vektör olsun.

import numpy.linalg as lin
from mpl_toolkits import mplot3d
from stl import mesh

mesh1 = mesh.Mesh.from_file('../../sk/2020/08/shapes/Prism_hexagon.stl')

def plot_vector1(fig, orig, v, color='blue'):
   '''
   baslangıcı orig olan v büyüklüğü/yönünde olan vektorü çiz
   '''
   orig = np.array(orig); v=np.array(v)
   ax.quiver(orig[0], orig[1], orig[2], v[0], v[1], v[2],color=color)

def plot_vector2(fig, torig, tend, color='blue'):
   '''
   baslangic torig bitis tend olmak uzere bir vektor ciz
   '''
   v = tend - torig
   ax.quiver(torig[0], torig[1], torig[2], v[0], v[1], v[2],color=color)

tidx = 7
f0 = np.array([40,20,10])
f1 = mesh1.vectors[tidx][0]
cog = mesh1.get_mass_properties()[1] # cog = agirlik merkezi (center of gravity)

a = f1-f0
b = cog-f0
flin = (a.dot(b) / (lin.norm(b)**2))*b

tau = np.cross(f1-cog,f1-f0)
fig, ax = plt.subplots(1, 1, subplot_kw={'projection': '3d'})
obj = mplot3d.art3d.Poly3DCollection(mesh1.vectors)
obj.set_edgecolor('k')
obj.set_alpha(0.3)
ax.add_collection3d(obj)
plot_vector2(ax, f0, f1)
plot_vector1(ax, cog, tau, color='cyan')
plot_vector1(ax, f0, flin, color='cyan')
ax.plot(cog[0], cog[1], cog[2], 'gs')
ax.set_xlim(30,70);ax.set_ylim(-10,30); ax.set_zlim(-10,30)
ax.text(65,0,8,r'$\tau$',fontsize=20)
ax.text(35,5,8,r'$F$',fontsize=20)
ax.text(35,5,-3,r'$F_{cog}$',fontsize=20)
ax.view_init(elev=20, azim=40)
plt.savefig('phy_005_basics_06_01.jpg')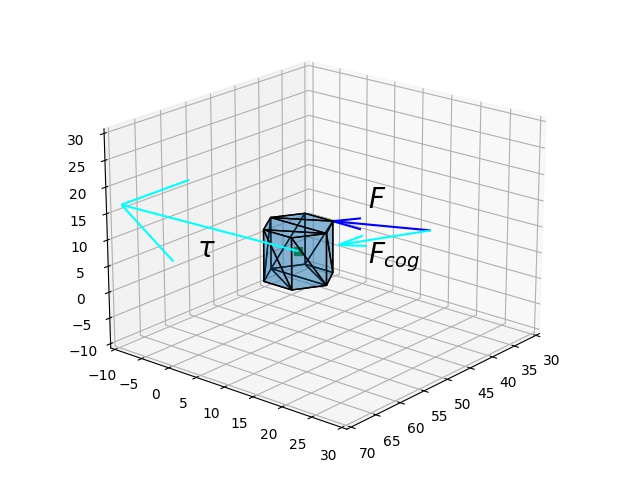

Kuvvet uygulama yönü ve onun kütle merkezine doğru olan yansıması gösterildi, ayrıca yerçekim merkezi de bir ufak küp olarak nesne içinde belirtiliyor. Merkeze olan bileşen kuvveti gösteren vektörün ucu muhakkak merkeze dokunuyor olmalı, biz burada gösterim amaçlı olarak hem kuvveti hem de bileşenini aynı başlangıçtan gösterdik. Yansıtma hesabı için bkz [6]. Tork vektörü de hesaplanıyor, ve COG (agirlik merkezi -center of gravity) çıkışlı olarak gösteriliyor. Objenin dönüşü bu vektör etrafında ve vektörün büyüklüğüne oranlı hızda olacaktır.

Alttaki kodlarla bir dış kuvvet uygulanan objenin hareketini inceleyeceğiz. Obje uzayda hareketsiz duruyor, yerçekim etkisi yok. Önce ilk uygulanan kuvvet etkisinden bahsedelim. Daha önceki yazıda ilk uygulanan kuvveti direk hıza çevirmiştik, fakat kavramsal daha mantıklı olan geçiş kuvvet / tork ve onun ilk lineer ve açısal momentuma olan etkisidir.

Lineer momentum değişimi için \(t=0\) anında ve \(t_f - t_i = \Delta t\) süresinde etki eden \(F\) için

Yani ilk lineer ve açısal momentumu üstteki \(\Delta p\) ve \(\Delta L\) olarak başlangıçta sıfır olan \(p\) ve \(L\) değerlerine ekleyeceğiz.

İlk değerler hesaplandıktan sonra simülasyonun geri kalanında \(t>0\) için Euler entegrasyonu ile güncellemeler yapılacak.

Bir püf nokta atalet matrisi tersi \(J^{-1}\) hesabı [1, sf. 467] (bizim daha önce \(I^{-1}\) olarak işlediğimiz değer). Bunun için

kullanabileceğimizi biliyoruz. \(J_{cisim}^{-1}\) değeri objenin başlangıçtaki atalet matrisi, yani dönüş matrislerini kullanarak atalet matrisi tersini sürekli güncelleyebiliyoruz. Böylece güncellenen \(J^{-1}\) ile herhangi bir anda açısal hız \(w\)’yi hesaplayabiliyoruz. \(L = J w\) olmasından hareketle,

Tabii hızın kuaterniyon olarak temsil edilmesi lazım, açısal hızı üstteki \(w\) ile hesapladıktan sonra onu skalar değeri sıfır olan bir kuaterniyon yapıp onu mevcut yönsel duruş (ki o da kuaterniyon ile temsil ediliyor) ile çarpıyoruz, ve duruştaki değişimi elde ediyoruz, (1) formülünde gördük.

from mpl_toolkits import mplot3d
import numpy.linalg as lin, sys, copy, os
from stl import mesh
sys.path.append("../phy_073_rot"); import euclid

def plot_vector1(fig, orig, v, color='blue'):
   orig = np.array(orig); v=np.array(v)
   ax.quiver(orig[0], orig[1], orig[2], v[0], v[1], v[2],color=color)

def plot_vector2(fig, torig, tend, color='blue'):
   v = tend - torig
   ax.quiver(torig[0], torig[1], torig[2], v[0], v[1], v[2],color=color)

mesh = mesh.Mesh.from_file('../../sk/2020/08/shapes/Prism_hexagon.stl')
cog = mesh.get_mass_properties()[1]
tidx = 7

m = 1 # kg
p = np.ones(3) * 0 # lineer momentum
L = np.ones(3) * 0 # acisal momentum
w = np.ones(3) * 0 # acisal hiz
q = np.ones(3) * 0 # durus (orientation)
f0 = np.array([40,20,10])
f1 = mesh.vectors[tidx][0]
a = f1-f0
b = cog-f0
flin = (a.dot(b) / (lin.norm(b)**2))*b
x = cog
S1,S2,N = 0,5,20
dt = (S2-S1) / N
q = euclid.Quaternion(1,0,0,0)
Jbodyinv = lin.inv(mesh.get_mass_properties()[2]*0.1)
F_ext  = f1-f0
tau_ext = np.cross(cog-f1,f1-f0)

for i,t in enumerate(np.linspace(S1,S2,N)):
    fig, ax = plt.subplots(1, 1, subplot_kw={'projection': '3d'})
    # x ilk degeri cog, x degistikce cog'den ne kadar uzaklasmissa
    # o farki mesh.vectors uzerine eklersek figurde gorulen objeyi
    # o kadar yerinden oynatabiliriz.    
    R = q.get_rotation_matrix_3x3().to_numpy_array()
    currmesh = copy.deepcopy(mesh)
    currmesh.vectors = currmesh.vectors + (x - cog)
    currmesh.rotate_using_matrix(R)
    obj = mplot3d.art3d.Poly3DCollection(currmesh.vectors)
    obj.set_edgecolor('k')
    obj.set_alpha(0.3)
    ax.add_collection3d(obj)
    plot_vector2(ax, f0, f1)
    plot_vector1(ax, f0, flin, color='cyan')
    plot_vector1(ax, cog, tau_ext / 10, color='cyan')
    if t==0:
       # baslangicta p sifir, ve ilk F entegre edilerek ilk p
       # elde ediliyor. Ayni sekilde L.
       p = F_ext*dt
       L = tau_ext*dt
    x = x + dt*(p / m)
    R = q.get_rotation_matrix_3x3().to_numpy_array()
    Jinv = R.dot(Jbodyinv).dot(R.transpose())
    w = L.dot(Jinv)
    wq = euclid.Quaternion(0, w[0], w[1], w[2])
    qdiff = (wq * q).scalar_mul(1/2).scalar_mul(dt)
    q = q.add(qdiff).normalize()
    ax.set_xlabel('x');ax.set_ylabel('y');ax.set_zlabel('z')
    ax.set_xlim(30,70);ax.set_ylim(-10,30); ax.set_zlim(-10,30)
    ax.view_init(elev=20, azim=50)
    plt.savefig('img/out-%02d.jpg' % i)
    plt.close(fig)

os.system("convert -loop 0 -delay 30 img/*.jpg img/rbmove1.gif")

Not: STL objesinden gelen atalet matrisi \(J_{cisim}\) yani mesh.get_mass_properties()[2] değerinin 0.1 ile çarpılıp küçültülmesine dikkat. Bunun yapılmasının sebebi STL’den gelen \(J_{cisim}\) değerinin çok büyük olması idi, herhalde objenin birim değerleri çok küçüktü (mesela milimetre) ve bu sebeple değerler binlerde oluyordu. Fakat bu yüzden 1 kg üzerindeki lineer momentumun etkisi ilk açısal momentum değerinden çok daha büyük oluyordu, objenin dönmeye karşı “ataleti” çok büyük idi, seçtiğimiz kuvvet vektörü döndürmeyi sağlayamıyordu. Atalet matrisini suni şekilde biraz küçülterek bu problemi çözmüş olduk.

Üstteki yaklaşım Euler entegrasyonu kullandı. Runge-Kutta entegrasyonu kullanan kodlar alttadır.

Hareketin Katı-Gövde Denklemleri - 2