Temel Fizik 4 - Katı Gövde, Atalet Matrisi (Inertia Matrix), Tork

Parçacıklar, Çok Parçacıklı Sistemler, Katı Gövde (Rigid Body)

Kütle Merkezi

Küresel, birörnek parçacıklara uygulanan kuvvetin onların merkezine uygulandığı farzedilebilir, ya da parçacık sanki noktasal bir parçacık imiş gibi işlemler yapılabilir. Fakat bu faraziyeyi nasıl doğrularız? Ayrıca farklı şekillerde, homojen bir maddeden oluşmayan objeleri nasıl idare ederiz?

Burada kütle merkezi (center of mass) kavramı yardımcı olur, mesela $N$ tane $m_i$ kütlesine sahip parçacığın kütle merkezi

$$ r_c = \sum_{i=1}^{N} \frac{m_i}{m} r_i = \frac{1}{m} \sum_{i=1}^{N} m_i r_i $$

ile hesaplanabilir. Bu bir nevi bir ağırlıklı ortalama. $O$ bir referans noktasıdır, mesela kordinat orijini, $r_i$ ise $O$'dan parçacık konumuna işaret eden bir vektör, parçacığın yeri [7, sf. 77].

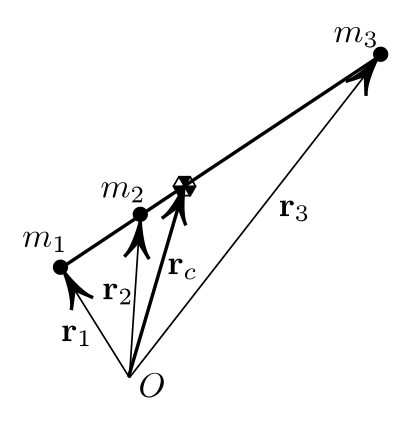
Dikkat edersek parçacıklar ayrı ayrı duruyor, ama birazdan göreceğiz ki bu parçacıklar tek bir katı gövde objenin içinde olsalar da hesap geçerli oluyor. Hatta gövde katı olmasa bile, mesela titreşen, salınımda olan moleküllere, öğelere sahip objeler bile belli şartlara uyuyorlarsa aynı kurallar ile idare edilebiliyorlar. $F_{ij}$ her $i$ parçacığının $j$ parçacığından hissettiği kuvvet olsun, ve $F_i$ değeri de $i$ parçacığı üzerindeki tüm dış kuvvetlerin toplamı olsun. Newton'un ikinci kuralını her parçacık için yazarsak, $i$'nin hissettiği tüm kuvvetlerin toplamı solda kütle çarpı ivmeye eşit olacaktır,

$$ m_i \ddot{r}_i = \sum_{j \ne i} F_{ij} + F_i $$

ki $\ddot{r} = \mathrm{d}^2 / \mathrm{d} t^2 r$, zamana göre ikinci türev anlamında.

Fakat Newton'un etki-tepki üçüncü kuralına göre her parçacık uyguladığı kuvvet kadar ters yönde geri bir kuvvet hisseder, yani $F_{ij} = -F_{ji}$, olmalı, o zaman her iki tarafta tüm $i$'ler üzerinden bir toplama yapınca parçacık sistemindeki bu "iç" kuvvetler birbirini nötralize etmeliler, üstteki formülden geriye kalanlar,

$$ \sum m_i \ddot{r}_i = \sum F_i $$

olur. $\sum F_i$ değeri sisteme uygulanan tüm dış kuvvetler $F_{ext}$ olarak görülebilir. Sol tarafı $m$ ile hem bölüp, hem çarpalım,

$$ m \frac{\mathrm{d}^2}{\mathrm{d} t^2} \underbrace{\sum \frac{m_i}{m} r_i}_{r_c} = F_{ext} $$

İşaretli yerde bir $r_c$ elde ettiğimizi görüyoruz, o zaman

$$ m\ddot{r}_c = F_{ext} $$

diyebiliriz, yani tüm sistemin kütle merkezi tek bir parça gibi görülebilir, hesaplarda $m$ ve $F_{ext}$ ile beraber bu şekilde kullanılabilir, ki o merkezin ivmesi $\ddot{r_c}$ olacaktır.

İşin ilginç tarafı bu sistem ayrı ayrı parçalar olsun, ya da aynı katı gövde içindeki "bloklar" olsun bu hesap yine işliyor olacaktır, çünkü düşünürsek bir katı obje içindeki blokların, parçacıkların da birbiri üzerinde kuvvetleri de birbirini nötralize ederler, hatta katı olmayan ama parçaları titreşen obje için de aynı argüman, ve aynı formül kullanılabilir.

Toplam lineer momentum oldukça basit,

$$ P = \sum_i p_i = \sum_i m_i \dot{r}_i = M \dot{R} $$

Yani kütle merkezi üzerinden tüm kütle için bir momentum kullanılabilir.

Toplam Açısal Momentum

Tek parça için $l = r \times p$ olan momentumların bir parçacık sisteminde hesaplamak istersek daha önce lineer momentumda olduğu gibi toplam alabiliriz,

$$ L = \sum_{i=1}^{N} l_i = \sum_{i=1}^{N} r_i \times p_i $$

Bir katı gövdede hesap aynıdır, ve daha önce gördüğümüz kütle için parçacıkların birbiri üzerine uyguladığı kuvvetlerin iptal olması durumunu, parçacıkların birbirine uyguladığı torkların iptali olarak açısal ortama taşıyabiliyoruz, yani üstteki formül doğru, detaylar için [8, sf. 94].

Kütle merkezinin toplam açısal momentumun hesabında oynadığı rol biraz daha karmaşık ama bir o kadar önemli [8, sf. 368].

Yine bir katı gövde düşünelim, $N$ tane her biri $m_i$ ağırlığında parçacıktan oluşuyor olsun, altta resmedildiği gibi, kütle elipsoid şeklinde.

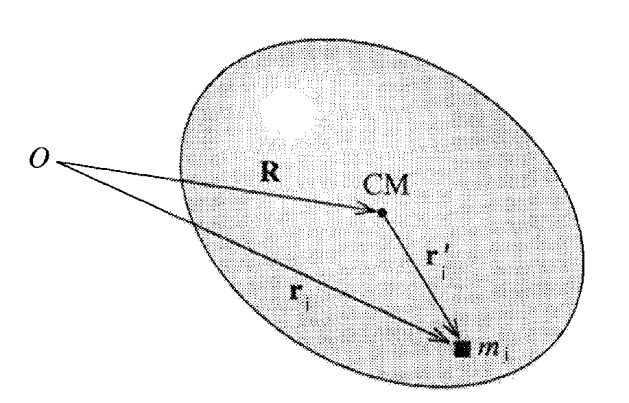
$m_i$'nin herhangi bir şekilde seçilen referans / orijin noktası $O$'ya göre olan yeri $r_i$ ile gösteriliyor. Kütle merkezi (center of mass) CM ile, CM'nin $O$'ya göre yeri $R$, $m_i$'nin CM'ye izafi olarak yeri $r_i'$. Yani

$$ r_i = R + r_i' \qquad (7) $$

doğru olacak. Şimdi $O$'ya göre parçacık $i$ için açısal momentum hesaplarsak

$$ l_i = r_i \times p_i = r_i \times m_i \dot{r}_i $$

$l,p,r$ vektörsel değerler.

O zaman $O$ referansina izafi olarak toplam momentum

$$ L = \sum_i l_i = \sum_i r_i \times p_i = \sum_i r_i \times m_i \dot{r}_i $$

Eğer (7) denklemini üste sokarsak,

$$ L = \sum_i (\dot{R} + \dot{r}_i') \times m_i (\dot{R} + \dot{r}_i' ) $$

Şu kuralı [8] kullanarak

$$ (A + B) \times (C+D) = (A \times B) + (A \times C) + (B \times C) + (B \times D) $$

açılımı yapabiliriz,

$$ = \sum_i (\dot{R} + \dot{r}_i') \times (m_i \dot{R} + m_i \dot{r}_i' ) $$

$$ = \sum_i (R \times m_i \dot{R}) + (R \times m_i \dot{r}_i') + (r_i' \times m_i \dot{R}) + (r_i\ \times m_i \dot{r}_i')
$$

$M = \sum_i m_i $ diyelim, ki $M$ tüm kütle,

$$ L = R \times M\dot{R} + R \times \sum m_i \dot{r}_i' + (\sum r_i' m_i) \times \dot{R} + \sum r_i' \times m_i \dot{r}_i' \qquad (8) $$

Bu son denklem üzerinde oldukca fazla basitleştirme mümkün. Mesela üçüncü terimde parantezler içinde olan formül sıfıra eşit, niye? Kütle merkezi formülünü yazarsak,

$$ R = \frac{1}{M} \sum m_i r_i $$

$$ MR = \sum m_i r_i $$

Aynı şekilde izafi açılımı yapalım,

$$ = m_i (R + r_i') = \sum m_i R + \sum m_i r_i' $$

Yani

$$ MR = MR + \sum m_i r_i' $$

elde ederiz, ve bu formülün doğru olması için $\sum m_i r_i' = 0$ olması gerekir.

Yani (8) denkleminin üçüncü terimi sıfır. O terimin türevini alırsak ikinci terimin elde edileceğini görürüz, o zaman o da sıfır olur. Geriye kalanlar,

$$ L = R \times P + \sum_i r_i' \times m_i \dot{r}_i' $$

Birinci terim kütle merkezinin $O$'ya göre açısal momentumu, ikincisi hareketin kütle merkezine göre olan açısal momentumu. Üstteki formül sayesinde bir katı gövdenin açısal momentumunu iki parçaya bölerek düşünmek mümkün oluyor.

CM Torku CM Açısal Momentumu

Şimdi şu soruyu soralım: katı gövdenin açısal momentum değişimi (dönüşsel kuvvet, tork) ona uygulanan, ve yine onun CM'sine göre uygulanmış dış torka eşit midir? Cevap evet olacak ama bu aslında ilk başta çok bariz olmayabiliyor, çünkü CM ivmeleniyor, bu eşitlik o durumda da geçerli olur mu? Fakat CM ivmeleniyor olsa bile cevap değişmiyor.

İspatlamak için CM etrafındaki açısal momentumu formülize edelim [9, sf 37],

$$ L_{CM} = \sum r_i' \times m_i \dot{r}_i' $$

CM etrafında uygulanan tork, üstteki açısal momentumun zamansal türevidir,

$$ \dot{L}_{CM} = \sum \dot{r}_i \times m_i \dot{r}_i' + \sum r_i' \times m_i\ddot{r}_i' $$

Eşitliğin sağındaki ilk terim sıfır çünkü iki paralel vektörün çapraz çarpımı sıfırdır. Kalanlarla devam edersek, $r_i = r_i' + R$ olduğu için oradan $\ddot{r}_i = \ddot{r}_i' + \ddot{R}$ ve oradan $\ddot{r}_i' = \ddot{r}_i - \ddot{R}$ diyoruz, üstteki ikinci terimde yerine koyunca

$$ = \sum r_i' \times m_i (\ddot{r}_i - \ddot{R}) $$

$$ = \sum (r_i' \times m_i \ddot{r}_i) - (r_i' \times m_i \ddot{R}) $$

$$ = \sum (r_i' \times m_i \ddot{r}_i) - \sum (r_i' \times m_i \ddot{R}) $$

İlk terimde kuvvet tanımı görülüyor,

$$ = \sum (r_i' \times F_i ) - \sum (r_i' \times m_i \ddot{R}) $$

İkinci terimde $m_i$ yer değiştirebilir,

$$ = \sum (r_i' \times F_i ) - \sum (m_i r_i' \times \ddot{R}) $$

$\sum m_i r_i'=0$ olduğunu hatırlarsak ikinci terim kaybolur,

$$ = \sum r_i' \times F_i $$

Geriye kalan dışarıdan CM etrafında uygulanan tork tanımı değil midir? Evet. O zaman dışarıdan CM etrafında uygulanan tork ile başladığımız ifade $\dot{L}_{CM}$ yani CM etrafındaki momentum değişimi arasındaki eşitliği ispatlamış olduk.

Atalet Matrisi (Inertia Matrix, Tensor)

Bir objenin havaya fırlatıldığını düşünelim, fırlatma sırasında dönüş te var, çetrefil bir hareket sözkonusu yani. Fakat şimdiye kadar gördüğümüz teknikler ile hala bu hareketi analiz edebiliriz, hem lineer momentum, hem de açısal momentum kütle merkezi odaklı olarak analiz edilebiliyor. Herhangi bir katı gövde, cisim şeklini ve hareketi analiz için şimdi bazı genel formülleri ortaya koyalım.

Gövdenin açısal momentumu $L$ için [1, sf. 379],

$$ L = \sum m_i r_i \times v_i $$

ki $L,r,v$ vektör. $v = \omega \times r$ eşitliğini üste sokarsak,

$$ L = \sum m_i r_i \times (\omega \times r_i) \qquad (1) $$

Şimdi bu son ifadenin her vektörü öğelerini kullanarak açılımını yapalım böylece başka bir forma erişmeyi umuyoruz. $\omega = [\begin{array}{ccc} \omega_x&\omega_y&\omega_z \end{array}]^T$ ve $r = [\begin{array}{ccc} x&y&z \end{array}]^T$ öğelerini kullanacağız, ve üstteki formülün $A \times (B \times C)$ formunda olduğunu farkediyoruz, o zaman genel bir $r \times (\omega \times r)$ üzerinde BAC-CAB açılımı yapmayı deneyebiliriz, bu açılım hatırlarsak,

$$ A \times (B \times C) = B(A \cdot C) - C(A \cdot B) $$

idi. Kendi denklemimiz üzerinde bu açılım

$$ r \times (\omega \times r) = \omega (r \cdot r) - r(r \cdot \omega) $$

şeklinde olacaktır. Açılımı yapınca 3 x 1 boyutunda bir vektör elde ediyoruz onun sadece ilk öğesine, $x$ için olan durumuna bakalım,

$$ r \times (\omega \times r)_x = \omega_x (x^2 + y^2 + z^2) - x(\omega_x x + \omega_y y + \omega_z z) $$

$\omega_x x^2$ iki yerden iptal olur, kalanlar,

$$ = \omega_x ( y^2 + z^2) - \omega_y xy + \omega_z xz $$

Her üç öğe için açılım yapınca,

$$ r \times (\omega \times r) = \left[\begin{array}{c} (y^2 + z^2) \omega_x - xy \omega_y - xz \omega_z \\ -yx \omega_x + (z^2 + x^2)\omega_y - yz \omega_z \\
-zx \omega_x - zy \omega_y + (x^2+y^2)\omega_z \end{array}\right] $$

Ve ana formülde $m_i$ çarpımı olduğunu unutmayalım,

$$ m r \times (\omega \times r) = \left[\begin{array}{c} m (y^2 + z^2) \omega_x - m xy \omega_y - m xz \omega_z \\ -m yx \omega_x + m (z^2 + x^2)\omega_y - m yz \omega_z \\
-m zx \omega_x - m zy \omega_y + m (x^2+y^2)\omega_z \end{array}\right] $$

Üstteki sonucu (1)'e sokunca, ve notasyonel olarak bazı rahatlıklar düşünerek, mesela $I_{xx} = \sum_i m_i (y_i^2 + z_i^2)$ gibi, ya da $I_{xy} = - \sum_i m x_i y_i$. Bunları da yerine koyunca, $L_x,L_y,L_y$ diyelim,

$$ L_x = I_{xx} \omega_x + I_{xy} \omega_y + I_{xz} \omega_z $$

$$ L_y = I_{yx} \omega_x + I_{yy} \omega_y + I_{yz} \omega_z $$

$$ L_z = I_{zx} \omega_x + I_{zy} \omega_y + I_{zz} \omega_z $$

Fakat bu son sonuç hala biraz sadeleştirilebilir. İfadeye bakarsak onu bir matris çarpı bir vektör çarpımı ile temsil edebiliriz gibi geliyor, hakikaten de

$$ I = \left[\begin{array}{ccc} I_{xx} & I_{xy} & I_{xz} \\ I_{yx} & I_{yy} & I_{yz} \\ I_{zx} & I_{zy} & I_{zz} \end{array}\right], \quad \omega = \left[\begin{array}{c} \omega_x \\ \omega_y \\ \omega_z \end{array}\right] $$

üzerinden $I \omega$ çarpımının (2) sonucunu vereceğini görebiliriz. Böylece gayet sade

$$ L = I \omega $$

ifadesine geri gelmiş olduk.

$I$, atalet matrisidir, ve her katı kütle şekline göre farklı olacak bir matristir. O zaman bir objenin açısal momentumunun nasıl olacağını hesaplamak için önce o objenin atalet matrisine hesaplamak gerekir.

Not: Üstte tork diye adlandırılan büyüklük, yani kuvvet çarpı bir merkeze olan uzaklık hesabı, bazı kaynaklarda moment diye geçer, mesela inşaat mühendisliğinde bükülme momenti (bending moment) sözünü görebiliriz. Bu terimi momentum ile karıştırmamak lazım, ki onun da açısal ve lineer çeşitleri var, bu farklı bir kavram.

Ataletin Asal Eksenleri (Principal Axes of Inertia)

Bir konu daha var tabii; dikkat edersek $I$ matrisini çekip çıkardığımız hesap bir $O$ referansını merkez alıyordu. "Genel bir $O$ olsun" dedik ve oradan türetmeye devam ettik. Fakat bazı referansların, yani dönüşün neyin etrafında olduğunun, her seçime göre farklı $I$'lara sebebiyet verebileceğini görmek gerekir. Lineer cebirsel olarak $L$ ile $\omega$'nin aynı yönü göstermesi için $I$'nin köşegen matris olması gerekir. Fakat elde köşegen matris olmasa da $\omega$'yi bizim değiştirerek, aynı refarans $O$'dan geçen ama farklı öyle bir yönü göstermektir ki, bu eksen etrafında bir köşegen $I$ elde edilsin ve hareket simetrik hale gelsin.

Bu hesap için özdeğer, özvektör hesabını yapmak lazım, ya da atalet matrisinin köşegenleştirilmesini [2] (diagonalization) gerçekleştirmek lazım. Eğer $I$ köşegen değil ise, öyle bir $\omega$ bulalım ki $L = I \omega$ hesabındaki $L$, $I \omega$ ile aynı yönü göstersin, yani

$$ I\omega = \lambda \omega $$

haline gelsin. Bu bir özdeğer problemi değil midir? Evet.

Örnek olarak [1, sf. 382]'deki $O$ etrafında dönen küp orneğini kullanalım,

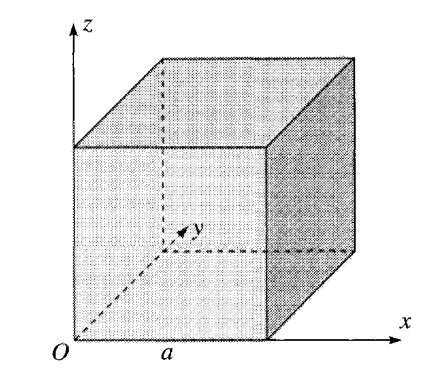
Bu referansa göre atalet matrisi

$$ I = \left[\begin{array}{rrr} 8 & -3 & -3 \\ -3 & 8 & -3 \\ -3 & -3 & 8 \end{array}\right] $$

olarak bulunmuş. Görüldüğü gibi $I$ köşegen değil. Kosegenlestirmek icin,

import numpy.linalg as lin
I = np.array([[8, -3, -3],
              [-3, 8, -3],
              [-3, -3, 8]])
e,evec = lin.eig(I)
print (e)
print (evec)
print (evec[:,0])

[11.  2. 11.]
[[ 0.81649658 -0.57735027  0.        ]
 [-0.40824829 -0.57735027 -0.70710678]
 [-0.40824829 -0.57735027  0.70710678]]
[ 0.81649658 -0.40824829 -0.40824829]

Demek ki yeni $I$ matrisi

$$ I = \left[\begin{array}{rrr} 11 & 0 & 0 \\ 0 & 2 & 0 \\ 0 & 0 & 11 \end{array}\right] $$

olmalı.

Üç tane $\omega$ vektörü elde edildi, bunlar tabii ki birbirine dik, hepsini grafikleyelim, yeşil çizgiler $x,y,z$ eksenleri olmak üzere,

from mpl_toolkits import mplot3d

def plot_vector(fig, orig, v, color='blue'):
   ax = fig.gca(projection='3d')
   orig = np.array(orig); v=np.array(v)
   ax.quiver(orig[0], orig[1], orig[2], v[0], v[1], v[2],color=color)
   ax = fig.gca(projection='3d')  
   return fig

fig = plt.figure()
axes = mplot3d.Axes3D(fig)
SCALE = 0.5
plot_vector(fig, [0,0,0],evec [:,0]*SCALE)
plot_vector(fig, [0,0,0],evec [:,1]*SCALE)
plot_vector(fig, [0,0,0],evec [:,2]*SCALE)
axes.view_init(elev=10, azim=200)
axes.set_xlim(-1,1)
axes.set_ylim(-1,1)
axes.set_zlim(-1,1)
axes.plot([0,1],[0,0],[0,0],color = 'g')
axes.plot([0,0],[0,1],[0,0],color = 'g')
axes.plot([0,0],[0,0],[0,1],color = 'g')
axes.locator_params(tight=True, nbins=4)
plt.savefig('phy_005_basics_04_02.png')

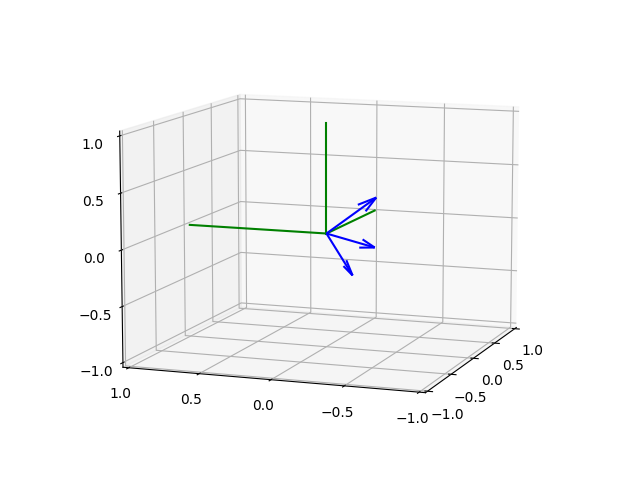
Rotasyon Matrisi ve Türevi

Bir 3 x 3 dönüş matrisi ile herhangi bir vektörü döndürebileceğimizi biliyoruz. Yersel taşıma daha da basit, 3 boyutlu bir vektör sadece, mevcut konuma ekleyerek yeni konumu elde ediyoruz.

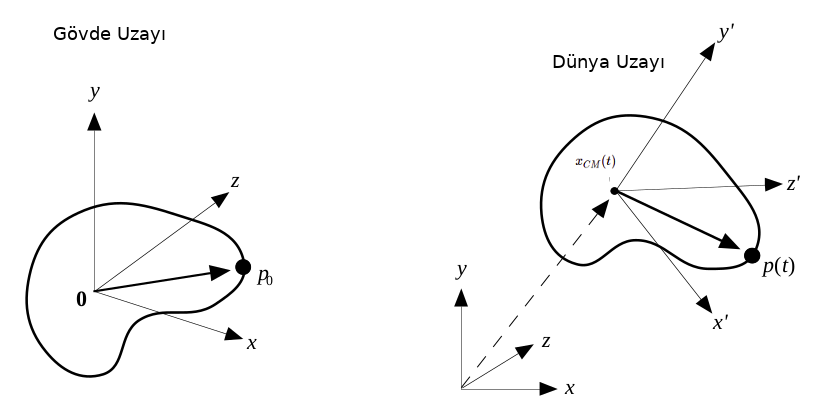
Bir katı gövdeyi parçacıkları üzerinden alırsak, ve bu gövdenin açısal dönüşsel olarak hangi yöne baktığını bir dönüş matrisi $R$ ile temsil edersek, her parçacık üzerinde bu işlemin uygulandığını düşünebiliriz. Ayrıca konumsal taşınma ve bakılan yön başlangıçtaki bir "gövde uzayı"na (body space) göre yapılabilir, gövdenin kütle merkezini dünya kordinatlarının (0,0,0) orijin noktasında ve yönü herhangi bir (başta belli) yöne doğru alalım, hareketler hep bu konuma referansla, onu değiştirecek şekilde düşünülebilir. Mesela gövde üzerindeki, gövde uzayındaki, herhangi bir $p_0$ noktasını düşünelim, $t$ anında bu noktanın dünya uzayındaki konumu

$$ p(t) = R(t) p_0 + x_{CM}(t) $$

ki $x_{CM}(t)$ bir yersel taşınma, ve $R(t)$ açısal dönüş. Tabii taşınma her zaman kütle merkezine uygulandığı için $x_{CM}$ aynı zamanda kütle merkezinin her $t$ anında dünya uzayında olduğu yeri de gösteriyor.

Türeve gelirsek, bir vektör $r$'nin orijin etrafında döndüğünü düşünelim. Herhangi bir anda bu dönüşün açısal hızı $\omega$ çapraz çarpımla hesaplanabilir,

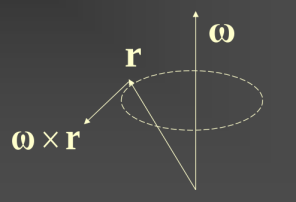
Hız tabii ki sonsuz küçük zamandaki yer değişimi olduğu için onu

$$ \frac{\mathrm{d} r}{\mathrm{d} t} = \omega \times r $$

olarak ta görebiliriz. Şimdi bir katı gövdeyi düşünelim, onun baktığı yön (orientation) bir matris $R$ içinde. Bu matrisin her kolonunda bir eksen var, ilk kolon $x$, ikinci $y$, vs. Eğer gövdenin baktığı yönü $R$ ile temsil ediyorsak tüm bu kolonlar gövde dönerken değişecektir. Eğer dönüş $\omega$ ise her eksenin açısal hızı $\omega$ demek, o zaman bu eksenlerin, $b,c,d$ diyelim, açısal hızı ayrı ayrı $\omega \times b$, $\omega \times c$, $\omega \times d$ olarak bulunabilir, ki bunların her biri aynı zamanda ayrı birer türevdir. Tüm matrisin türevi

$$ \frac{\mathrm{d} R}{\mathrm{d} t} = \tilde \omega \cdot R $$

ki $\tilde \omega$ ile $\omega$'yi eksi bakışımlı [4] bir matris hale getirdik, böylece çapraz çarpımı noktasal çarpım haline çevirmiş oluyoruz [5, sf. 9], [3].

Atalet Matrisi ve Dönüşler

Daha önce atalet matrisi $I(t)$'yi görmüştük,

$$ I(t) = \sum \left[\begin{array}{ccc} m_i (y_i^2 + z_i^2) & -m_i x_i y_i & m_i x_i z_i \\ -m_i y_i x_i & m_i (x_i^2 + z_i^2) & -m_i y_i z_i \\ -m_i z_i x_i & -m_i z_i y_i & m_i (x_i^2 + y_i^2) \end{array}\right] $$

Burada $x,y,z$ değerleri gövde uzayında, her nokta $r_i'$ için $x_i,y_i,z_i$ değerleri $r_i - \chi(t)$ içeriğiyle hesaplanıyor. Ayrıca bir obje dönerse, onun belli noktalarının eksenden olan uzaklıkları değişir ve farklı bir $I$ elde ederiz... fakat üstteki hesabı obje hareket ederken sürekli yapmak oldukca külfetlidir. Acaba $I$'nin bir baz kısmını hesaplasak, sonra dönüşe göre onu güncellesek olmaz mı?

Bunun bir yolu var [5, sf. 14]. $r_i'^T r_i' = x_i^2 + y_i^2 + z_i^2$ olduğundan hareketle, önceki $I$ denklemini şu şekilde yazabiliriz,

$$ I(t) = \sum m_i r_i'^T r_i' \left[\begin{array}{ccc} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{array}\right] - \left[\begin{array}{ccc} m_i x_i^2 & -m_i x_i y_i & m_i x_i z_i \\ -m_i y_i x_i & m_i y_i^2 & -m_i y_i z_i \\ -m_i z_i x_i & -m_i z_i y_i & m_i z_i^2 \end{array}\right] $$

Simdi en sağdaki matrise dikkat edelim, onu bir dış çarpım (outer product) olarak temsil edebiliriz, alttaki gibi,

$$ r_i' r_i'^T = \left[\begin{array}{c} x_i \\ y_i \\ z_i \end{array}\right] \left[\begin{array}{ccc} x_i & y_i & z_i \end{array}\right] = \left[\begin{array}{ccc} x_i^2 & x_i y_i & x_i z_i \\ y_i x_i & y_i^2 & y_i z_i \\ z_i x_i & z_i y_i & z_i^2 \end{array}\right] $$

Bunu kullanarak ve 3 x 3 boyutlu birim matrisini $\overline{1}$ ile göstererek (normalde bu matris için $I$ notasyonu kullanılır ama o hard bu yazıda kapılmış durumda),

$$ I(t) = \sum m_i ((r_i'^T r_i') \overline{1} - r_i' r_i'^T) $$

Bu nasıl faydalı? Çünkü $r_i(t) = R(t) r_{0i} + x_{CM}(t)$ ki $r_{0i}$ başlangıçtaki kütlede $i$ parçacığın yeri, ve sabit, o zaman

$$ r_i(t) - x_{CM}(t) = R(t) r_{0i} = r_i'(t) $$

Şimdi $r_i'(t) = R(t) r_{0i}$ eşitliğini iki üstteki formülde kullanırsak,

$$ I(t) = \sum m_i ( (R(t) r_{0i})^T (R(t) r_{0i}) \overline{1} - (R(t) r_{0i}) (R(t) r_{0i})^T ) $$

$$ = \sum m_i ( r_{0i}^T R(t)^T R(t) r_{0i} \overline{1} - R(t) r_{0i} r_{0i}^T R(t)^T ) $$

$R(t)$ dikgen, ortonormal matris oldugu icin $R(t)^TR(t) = \overline{1}$

$$ = \sum m_i ( (r_{0i}^T r_{0i}) \overline{1} - R(t) r_{0i} r_{0i}^T R(t)^T ) $$

Üstteki formülde ikinci terimde $R(t) .. R(t)^T$ ifadesi var, bunu birinci terime de eklemek için, ve $r_{0i}^T r_{0i}$ bir tek sayı değer olduğu için ve $R(t) R(t)^T$'nin birim matris olmasından hareketle,

$$ = \sum m_i ( R(t) (r_{0i}^T r_{0i}) R(t)^T \overline{1} - R(t) r_{0i} r_{0i}^T R(t)^T ) $$

Böylece $R(t)$ ve $R(t)^T$ dışarı çekilebiliyor,

$$ = R(t) \left( \sum m_i (( r_{0i}^T r_{0i}) \overline{1} - r_{0i} r_{0i}^T \right) R(t)^T $$

Böylece parantez içindeki, $I_{body}$ denebilecek değerler parçacıkların gövdenin ilk konumundaki yerlerine (ve değişmeyen kütle $m_i$ değerine) göre hesaplanabileceği için, onu bir kez hesaplayabiliriz, ve sonra ona $R(t)$'leri uygulayarak istediğimiz güncel $I(t)$ değerini elde ederiz [5, sf. 15].

$$ I(t) = R(t) I_{body} R(t)^T $$

$I$'nin tersi $I_{body}^{-1}$ de gerekli (niye birazdan göreceğiz) fakat bu hesap ta başta hesaplanıp depolanabilir, çünkü

$$ I^{-1} = ( R(t) I_{body} R(t)^T )^{-1} $$

$$ (R(t)^T)^{-1} I_{body}^{-1} R(t)^{-1} $$

$$ = R(t) I_{body}^{-1} R(t)^T $$

$R(t)^T = R(t)^{-1}$ ve $R(t)^T = R(t)$ olduğunu hatırlayalım çünkü $R(t)$ orthonormal, dikgen bir matris.

Hareketin Katı Gövde Denklemleri

Artık elimizde bir gövdenin her bakımdan konumunu, statüsünü temsil etmek için yeterli matematik var. Bu konumu $\overline{X}(t)$ ile gösterebiliriz,

$$ \overline{X} = \left[\begin{array}{c} x_{CM}(t) \\ R(t) \\ P(t) \\ L(t) \end{array}\right] $$

Momentum $P(t) = v(t) M$ olduğu için $v(t) = \frac{P(t)}{M}$.

$I(t)$'yi yukarıda gördük, $I(t) = R(t) I_{body} R(t)^T$.

$L(t) = I(t) \omega(t)$ olduğu için $\omega(t) = I(t)^{-1} L(t)$

Hepsini biraraya koyunca $\overline{X}$'nin türevi

$$ \frac{\mathrm{d}}{\mathrm{d} t} \overline{X}(t) = \frac{\mathrm{d}}{\mathrm{d} t} \left[\begin{array}{c} x_{CM}(t) \\ R(t) \\ P(t) \\ L(t) \end{array}\right] = \left[\begin{array}{c} v(t) \\ \tilde \omega \cdot R(t) \\ F(t) \\ \tau(t) \end{array}\right] $$

Kaynaklar

[1] Taylor, Classical Mechanics

[2] Bayramlı, Lineer Cebir, Ders 22

[3] Rotenberg, CSE169: Computer Animation, UCSD

[4] Bayramlı, Lineer Cebir, Ders 5

[5] Witkin, Physically Based Modeling

[7] Levi, Classical Mechanics with Calculus of Variations and Optimal Control

[8] Bayramlı, Cok Degiskenli Calculus, Ders 3

[9] Taylor, Classical Mechanics Problem Solutions