
Babil medeniyetinden dikkatli ölçmeyi ve gözlem yapmayı öğrenen eski Yunanlılar, tabiatı, mantıklı analiz dizisi ile anlamaya uğraştılar. Aristo’nun oldukça inandırıcı olan söylemlerinden biri olan, “dünya düz değildir”’den esinlenen günün diğer felsefecileri, “o zaman dünyanın çapı nedir?” gibi sorular ile uğraşmaya başladılar. Hayret verici olan bir gelişme, Eratostenes’in bu ölçüyü oldukça yakın olarak bulmasıdır, hem de yaşadığı şehir olan İskenderiye’den dışarı ayak bile basmadan! Kullanılan yöntem bazı kestirmeler ve temel alınan birkaç varsayım içeriyordu. Dünya mükemmel bir küredir (olmasa da onun hesabı için bu uygundu), güneşin ışınları birbirine paralel olarak yol alır, Syene şehri İskenderiye’nin 5000 stadya (bir ölçü birimir) kadar güneyde yer alır, vs.. Bu varsayımlardan yola çıkarak, Erotostenes bir matematiksel dünya yarattı ve bu dünya üzerinde geometri’nin uygulanabilir olduğunu gördü!

Günümüzde, aynen Yunanlı bilginlerin yaptığı gibi, bilim adamları etrafımızdaki dünyayı daha pragmatik bir seviyede anlayabilmek ve akabinde teknik sorulara çözüm bulabilmek için, etrafımızdaki dünyayı matematiksel terimlerle temsil etmeye devam ediyorlar. Gerçeği matematiksel bir dil ile ‘taklit etmeye’ yardım eden bu işlem ve düşünce şekline, matematiksel modelleme adı veriliyor.
Bir problemi matematiksel terimler kullanarak göstermenin bazı yararları var. İlki, altında olduğumuz şartları öne sürmemizi ve tanımlamamız için bizi zorlaması, ki bu güzel bir şey. Gerçek dünyada olmakta olan problemler çetrefilli olduklarından, hangi değişkenlerin çözümümüz için önemli, hangisinin önemsiz olduğunu daha matematiksel uygulama başlamadan kararlaştırmak önemli. Bu seçim yapıldıktan sonra, genelde bazı kanunlar ve kuramlar kuruluyor ve bu varsayımlar, modelimizin idealleştirilmiş hali adı altında irdelenmeye başlanıyor.
Matematik’in en önemli yararı, mantıksal sonuçlara varabilmek için elimizdeki varsayımlardan başlayarak bu formülleri değişimden geçirmemize yardım eden temel teknikler vermesi. Böylece elimize analiz yapabilmemiz için sağlam bir temel geçiyor, aradığımız sonucun ne olduğunu baştan tam kestirmesek bile, bu modelleme işlemi bize yolda yardım edecek araçlar sağlıyor.
Ayrıca matematiğin, bilgisayarlar tarafından sayısal cevaplar alınabileceği bir ortam sağlaması da önemli bir avantaj.
Etkili matematiksel modeller kurmak oldukça yetenek isteyen bir iş, tasavvur ve tarafsız irdeleyebilme kabiliyeti gerektiriyor. Daha önceden kurulmuş olan öteki modelleri örnek olarak incelemek, modelleme sürecinin nasıl bir şey olduğunu hissetmek için yararlı olabilir. Revaçta modellemeyi öğreten çok güzel kitaplar ve makaleler var. Bu yazımızda bizim odaklanacağımız, birinci derecen türevsel denklem içeren matematik modelleri olacak. İzleyeceğimiz modelleme işleminin ana hatları şöyle olacak.
Problemi Formüllere Dök
Bu safhada amacımız bir formülü kurmak. Böylece cevabın matematiksel olarak ‘bulunabileceğini’ umuyoruz. Tabii bu işlem hem matematiği hem de problem alanını bilmemizi gerektiyor. Bu seviyede, matematikçi olmasa bile problem alanında uzman olanlar kimseler ile konuşmanız yararlı olabilir. Ayrıca problem alanını anlatan eserleri okumanız iyi olacaktır.
Modeli Geliştir
Burada yapılacak iki şey var. İlk önce hangi değişkenler önemli, hangiler değil ona karar vermeniz gerekiyor. Önemli olanların arasından, bazıları bağımlı bazıları bağımsız değişken olarak tanımlanacaklar. Önemsiz değişkenleri şöyle farketmeniz mümkün; modellenen süreç üzerinde hiç etkisi olmayan değişkenler sizin için önemli değildir ve atılabilir. Mesela, binadan aşağı düşen bir topun hareketini incelemek istiyorsanız, topun hangi renkte olduğu modeliniz için önemsizdir.
Bağımsız değişkenler modeli etkileyebilecek, modele giriş olarak verilebilecek değerlerden seçilir. Yere düşen cisim için, cismin şekli, kütlesi, başlangıç noktası, başlangıç hızı, ve hangi zamanda bırakıldığı bu tür bağımsız değişkenlerdendir. Bağımlı değişkenler, adı üzerinde, değerleri bağımsız değişkenlere bağlı olan fakat, gene de model için önemli olan değişkenlerdir. Yere düşen cisim için bunlar hız, katledilen mesafe, yere çarpma zamanı gibi değişkenler bağımlı değişkenler arasında sayılabilir.
İkinci yapmak gereken şey, bu değişkenler arasındaki bağlantıları bulmak (mesela birinci derece türevsel denklem kurarak). Bunu yapmak problem alanı hakkında bilgi ve vizyon gerektirir. Taslak bir modelle başlanabilir, ve testler sonucunda modeli rafine etmek mümkündür. Mesela yukarıdaki örnek için başlangıçta sürtünme kuvvetini hesaba katmayabiliriz, fakat ileride daha net sonuçlar için sürtünmeyi modele eklemek gerekebilir.
Modeli Test Et
Modeli hemen test verileri ile ‘doğrulamaya’ uğraşmadan önce, şunlara tekrar göz atalım.
Nüfus Artış Modeli
Bir ülkenin nüfus artışını nasıl tahmin edebiliriz? Eğer bir gurubun nüfus artışını tahmin etmek istiyorsak, bu gurubu her dış etkiden uzak izole bir kapalı kutu halinde düşünebiliriz. Bu kutu mesela biyolojide Petri tabağı denen bir ortam, ya da günlük hayatta bir ada olarak tanımlanabilecek bir ortam olabilir. Böylece nüfus artışını izole bir şekilde ‘tek odada’ incelememiz mümkün olacak.
Diyelim ki, \(p(t)\), \(t\) zamanında ölçülecek olan nüfusu veriyor olsun. Şimdi çoğalma (doğum) ve azalma (ölüm) hızlarını hesaplayalım.
Örnek olarak şöyle düşünelim, bir bakteri kendini ikiye bölerek çoğalır. Bizim modelimiz için de, büyüme hızının, o anki mevcut nüfusa oranlı olduğunu varsayalım. Bu varsayım bakterilerin büyüme şekli ile tutarlı. Büyüyecek yer ve yeteri kadar yiyecek olduğu sürece, bakteriler büyüyeceğini biliyoruz. Bir diğer varsayım da şöyle olsun, ölüm oranı sıfır. (Unutmayalım ki, hücre bölünmesinde ebeveyn hücre ölmez, iki hücre haline gelir). Yani bakteri nüfusu için bir model şöyle olabilir.
\[ \frac{dp}{dt} = k_1p\]
\[ p(0) = p_0 \]
\(k_1 > 0\) olarak tasavvur edeceğiz. \(k_1\) büyüme oranı ‘sabitidir’. \(p_0\), nüfusun \(t = 0\) (yani başlangıçtaki) sayısıdır. Şimdi bakterilerden, insan nüfusuna gelelim. İnsan nüfusu için hiç ölmeme varsayımı tabii ki yanlış! Fakat, insanların sadece doğal sebeplerden olduğunu varsayarsak, ölüm oranının da o anki nüfus sayısına orantılı olduğunu düşünebiliriz. Bu yüzden, ilk denklemi değiştirip, şu hale getiriyoruz.
\[ \frac{dp}{dt} = k_1p - k_2p = (k_1-k_2)p = kp\]
\(k_2\) olarak nitelenen sabit, ölüm oranı olarak temsil edildi. \(k_1\)’in her zaman \(k_2\)’den büyük olduğunu farzedersek, asâgıdaki model çıkar.
\[ \frac{dp}{dt} = kp \]
\[ p(0) = p_0 \]
Birçok k sabiti kullanılmış olması aklınızı karıştırmasın. Doğum ve ölüm oranlamaları değişik sabitler gerektiyor, ama önemli olan bir ‘sabit’ kullanıldığını farketmek. Sonuçta demeye çalıştığımız nüfus ile nüfus büyümesi arasında doğrusal bir bağlantı olması. Sabite ihtiyacamız da buradan geliyor.
Elimize geçen son formül, ünlü bir formüldür, Maltezyen ya da nüfus artışının üstel (exponential) kanunu olarak bilinir. Denklem ayırılabilir olduğu için, işlemden geçirip p fonksiyonunu bulmak mümkün.
\[ \frac{dp}{dt} = kp, p(0) = p_0 \]
\[ \frac{dp}{p} = kdt \]
\[ \int \frac{dp}{p} = \int k \mathrm{d} t\]
\[ ln p = kt + C \]
\[ p = e^Ce^{kt} \]
\[ e^C = C_1 \]
\[ p = C_1e^{kt} \]
Maltezyen modelini test etmek için, Amerika’nın nüfus artış verisini kullanabiliriz.
Sene Nufus Maltezyen Lojistik
1770 3.93 3.93 3.3
1800 5.31 5.19 5.30
1810 7.24 6.84 7.13
1820 9.64 9.03 9.58
1830 12.87 11.92 12.82
1840 17.07 15.73 17.07
1850 23.19 20.76 22.60
1860 31.44 27.39 29.70
1870 39.82 36.15 38.65
1880 50.16 47.70 49.69
1890 62.95 62.95 62.95
1900 75.99 83.07 78.37
1910 91.97 109.63 95.64
1920 105.71 144.67 114.21
1930 122.87 190.91 133.28
1940 131.67 251.94 152.00
1950 151.33 332.47 169.56
1960 179.32 438.75 185.35
1970 203.21 579.00 199.01
1980 226.50 764.08 210.46
1990 249.63 1008.32 219.77
2000 ? 1330.63 227.19Örnek 1
Eğer t = 0 değeri için 1790 senesini alırsak, son formüle göre şöyle p(t) formülü nasıl bulunabilir?
\[ p(t) = (3.93)e^{kt} \]
\[ p(100) = 62.95 = (3.93)e^{100k} \]
\[ k = \frac{ln(62.95)-ln(3.93)}{100} \approx 0.027737 \]
\[ p(t) = (3.93)e^{(0.027737)t} \]
\(p(t)\)’yi bulduk. Yukarıda ki verilerden formülü kontrol edersek, Maltezyen tahmini 1900 tarihine kadar tuttuğunu görürüz. Fakat 1900’den sonra tahmin edilen nüfusun çok fazla, bu yüzden modelin işlemediğini görüyoruz.
Acaba model niye her zaman için işlemedi? Düşünelim. Model, nüfus çok arttıktan sonra bozulmaya başladığına göre, nüfus fazlalığı ile alakalı, ve bizim modele almadığımız bir faktör var demektir.
Maltezyen modeli, sadece doğal sebeplerden olan ölümü göz önüne almıştı. Öteki ölüm sebepleri de önemli olabilir, mesela yiyecek darlığından olan ölümler, yeterli sağlık malzemesi olmaması, ilaç yokluğundan olan ölümler, bulaşıcı hastalılar ya da suç işleyen insanlar yüzünden ölenler olabilir.
Bu tür faktörler insanlar arasında etkileşim gerektirdiği ve belli kaynaklara olan yarışma sırasında vuku bulan ölme durumlerı olduğu için, modele, ikili ilişkilerin de dikkate alındığı bir şekilde genişletmemiz gerekiyor. Yani, p sayısındaki bir nüfus için, p(p - 1) kadar ikili ilişki olduğunu düşünürsek, o zaman bu ikili ilişki ve yarış sonucundaki ölüm oranını şu şekilde modelleyebiliriz.
\[ \frac{dp}{dt} = ap - bp^2 \]
Burada \(p\) ve \(p^2\) ifadelerinin katsayıları, sabitleri değişik, çünkü bir sabit normal doğum ölümü, diğeri ise kaynaklara olan yarıştaki ölümler seçildi.
Şimdi biraz notasyon değişikliği, Cebirsel işlemleri kolaylaştırmak için sabitlerde biraz oynama yapacağız. \(a = k\), ve \(b = k/K\) diyelim.
\[ kp - \frac{k}{K}p^2 = \frac{dp}{dt} \]
\[ kp (1 - \frac{p}{K}) = \frac{dp}{dt} \]
Değişken ayırma (seperation of variables) yöntemini kullanırsak
\[ \frac{dp}{p(1-p/K)} = k \ dt\]
İki tarafın da entegralini alalım
\[ \int \frac{dp}{p(1-p/K)} = \int k \mathrm{d} t\]
\[ \int \frac{1}{p(1-p/K)}dp = \int k \mathrm{d} t\]
Eşitliğin sol tarafında entegralin içindeki ifadede hem bölüm, hem böleni \(K\) ile çarparsak
\[ = \frac{K}{p(K-p)} \]
Bunun üzerinde kısmi kesirler yöntemini (partial fractions method) kullanabiliriz, özellikle bölümdeki çarpanların toplamının bölümde olduğu durumlarda, ki bizim örneğimizde bu \(p + K - p = K\), bu ifadeyi ayırmak çok kolay, kısmi kesirlerin bölümü hemen 1 olabilir
\[ = \frac{1}{p} + \frac{1}{K-p}\]
Entegralde yerine koyalım
\[ \int \frac{1}{p} + \frac{1}{K-p} \mathrm{d} p = \int k \mathrm{d} t\]
\[ \int \frac{dp}{p} + \int \frac{dp}{K-p} = \int k \mathrm{d} t \]
\[ ln|p| - ln|K-p| = kt + C \]
\[ ln \bigg| \frac{p}{K-p}\bigg| = kt + C\]
\[ ln \bigg| \frac{K-p}{p}\bigg| = -kt - C\]
İki tarafı \(e\) bazında hesaplarsak
\[ \bigg| \frac{K-p}{p}\bigg| = e^{-kt - C} \]
Eğer \(A = \pm e^{-C}\) alırsak
\[ \frac{K-p}{p} = A e^{-kt } \qquad (1) \]
\[ \frac{K}{p} - 1 = Ae^{-kt} \]
\[ \frac{K}{p} = 1 + Ae^{-kt} \]
\[ \frac{p}{K} = \frac{1}{ 1 + Ae^{-kt}}\]
\[ p(t) = \frac{K}{ 1 + Ae^{-kt}} \]
Final formüle eriştik.
Peki \(A\) nedir? Eğer (1) ifadesine \(t=0\) verirsek
\[ \frac{K-p(0)}{p(0)} = A e^{k \cdot 0} = A\]
\(p(0) = p_0\) diyelim
\[ \frac{K-p_0}{p_0} = A \]
Bu denklemin tahminleri çok daha iyi işleyecektir.
Elde ettiğimiz \(p(t)\) fonksiyonunu grafiklediğimiz zaman çıktı suna benzeyecektir.
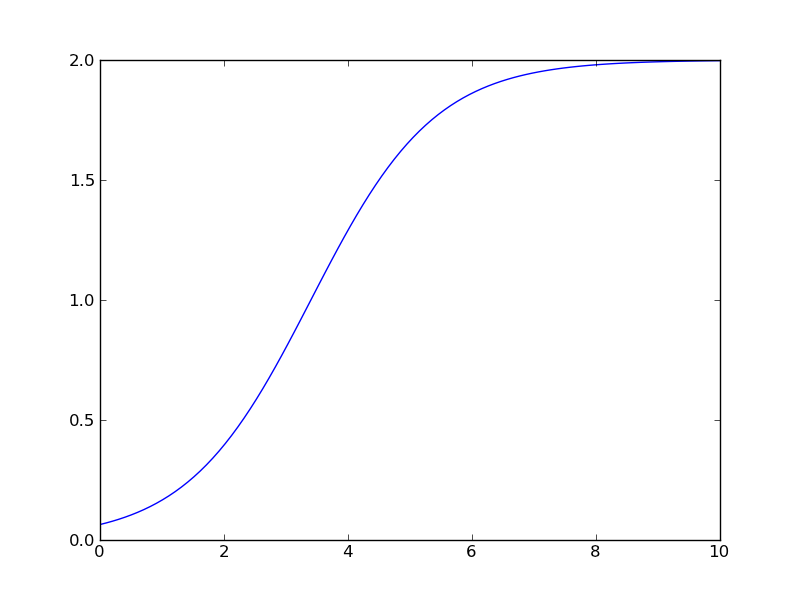
Elde edilen şekilde bir ‘S’ görüntüsünde, bu fonksiyona “S eğrisi’’ adı verildiği de oluyor. Bir diğer isim”Hill fonksiyonu’’.
Veri Uydurmak
Hill fonksiyonunu sayısal yöntemler kullanarak tarihi veriye
uydurarak, sabitlerini hesaplatmak mümkündür. Scipy paketindeki
scipy.optimize.leastsq fonksiyonu bu işi yapabilir.
Uydurmanın işlemesi için önce bir f tanımlanır, daha sonra
bu fonksiyonun gerçek veri ile arasındaki hatayı tanımlayan bir
fonksiyon verilir. Bu iki fonksiyon üzerinden veri uydurması
yapılacaktır.
# US population prediction, Logistic growth, Hill function
# Amerika nufus artisi, lojistik denklem
from scipy import optimize
def f(t,A,k,K):
return K / (1+A*np.exp(-k*t))
def resid(p, y, t):
A,k,K = p
return y - f(t,A,k,K)
t, x1 = np.loadtxt('us.txt', unpack=True)
t = np.linspace(0,10,len(t))
A0,k0,K0 = 1, 1, 1
[A,k,K], flag = optimize.leastsq(resid, [A0,k0,K0], args=(x1, t))
print (flag, A, k, K)
plt.plot(t, x1, 'ro')
t = np.linspace(0,20,len(t))
plt.plot(t, f(t,A,k,K), 'go')
plt.savefig('us.png')1 43.0658055581 0.427360301123 394.758729112Program işletildikten sonra grafik basılacak. Grafikte kırmızı noktalar gerçek veri, yeşil noktalar ise uyumu yapılmış fonksiyonun gelecek yıllar için gösterdiği tahmindir.
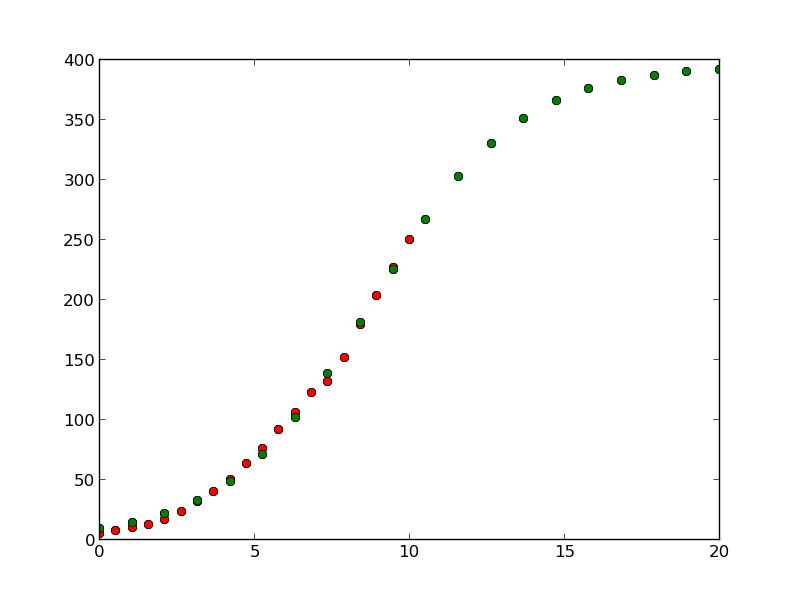
Sonuç
Bu yazıda hem model kurmanın ve türevsel denklemlerin yararlarını gördük. Türevsel denklem kurarken düşünülmesi gereken, \(dp/dt\) görünce ‘oran’ düşünmek, yani akla ‘değişim’ getirmek. Tabii daha türevleri daha detaylı anlayabilmek için (ispatı ile birlikte) limitlerin kuramı yararlı olur, fakat unutmayalım ki limitlerin ispatı için yetişinceye kadar yüzyıllar geçmişti! Calculus’un tam ispatı daha gelmeden, mühendisler ve bilim adamları türevleri ve entegralleri kullanıyorlardı.
Calculus, dinamik olan sistemler için kullanılır, yani değişmekte olan sistemler için gereklidirler. Calculus’un tarihinin fizik ile yakın alakası bundandır.
Kaynaklar
[1] Lerma, Math 214-2 Integral Calculus Lecture Notes http://www.math.northwestern.edu/~mlerma/courses/math214-2-03f
[2] Chan, Scientific Scripting with Python for Computational Immunology