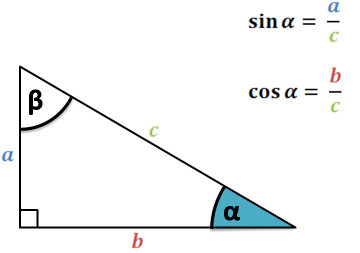
Basit bazı temel bilgilerin üzerinden geçelim. Sinüs, kosinüs, tanjant nedir? Karşı, komşu, hipotenüs kullanan bazı tanımlar akılda kalmış olabilir, mesela alttaki açı \(\alpha\) ve dik üçgenler için, karşı bölü hipotenüs sinüs, komşu bölü hipotenüs kosinüs, karşı bölü komşu tanjant.

Aslında tanjant’ın esas tanımı sinüs bölü kosinüs,
\[ \tan \alpha = \frac{\sin\alpha}{\cos\alpha} = \frac{a / c}{b / c} = \frac{a}{b} \]
bölen \(c\) iptal olduğu için geri kalanlar karşı bölü komşu.
Pitagor Kanunu
\(a^2 + b^2 = c^2\)
İspat
Dik üçgenimizi alıp yanyana koyarak bir kare oluşturuyoruz, artık hem dış çeperde bir kare var, ayrıca iç kısımda da bir kare var.
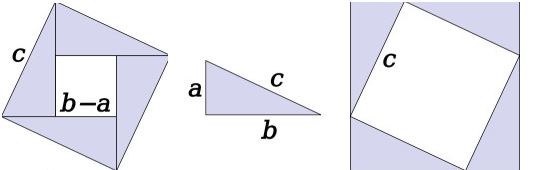
Bu karenin kenarları \(b-a\) büyüklüğünde, alanı tabii ki \((b-a)^2\). Büyük karenin alanı \(c^2\). Ama eğer büyük karenin alanını görülen beş tane parçayı toplayarak elde edebilirsek, Pitagor formülüne erisebiliriz.
\[ (b-a)^2 + 4 \frac{ab}{2} = (b-a)^2 + 2 ab = b^2 -2ab + a^2 + 2ab = a^2 + b^2 \]
Büyük kare eşitliğinden bu alan \(c^2\)’dir demiştik, o zaman
\[ c^2 = a^2 + b^2 \]
İspatı tamamlamış olduk.
Şimdi Pitagor kullanarak önemli bir trigonometrik eşitlik elde edeceğiz, alttaki dik üçgeni oluşturursak, \(\theta\) ne olursa olsun mavi renkli çemberin yarıçapı, ve dik üçgenin hipotenüsü 1 olacaktır, ve \(\sin\theta = a / 1\) olduğu için \(\sin\theta = a\), yani karşı kenar \(\sin\theta\), komşu kenar \(\cos\theta\).
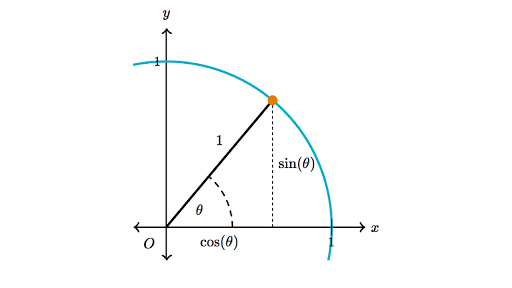
Bu kenar bilgilerine Pitagor üzerinden
\[ a^2 + b^2 = 1^2 \]
\(a,b\) yerine koyarsak,
\[ \cos^2\theta + \sin^2\theta = 1 \]
Kosinüsler Kanunu (Law of Cosines)
Bir üçgenin tüm kenar uzunlukları biliniyorsa o üçgenin tüm açılarını hesaplamak mümkündür, Kosinüsler Kanunu altında verilen üç formül bunu yapabilir [4].
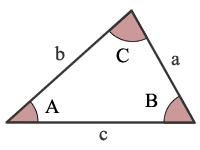
Formüller
\[ A = \cos^{-1} \left( \frac{b^2 + c^2 - a^2}{2bc} \right) \]
\[ B = \cos^{-1} \left( \frac{a^2 + c^2 - b^2}{2ac} \right) \]
\[ C = \cos^{-1} \left( \frac{a^2 + b^2 - c^2}{2ab} \right) \]
Gerçi son açıyı hesaplamaya gerek yok, \(A,B\) biliniyorsa üçüncü açı \(C\) 180 dereceden ilk iki açı toplamı çıkartılarak bulunabilir.
def tri_angles(a,b,c):
tmp = (b**2 + c**2 - a**2) / (2*b*c)
tmp = np.clip(tmp, -1, 1)
A = np.arccos(tmp)
tmp = (a**2 + c**2 - b**2) / (2*a*c)
tmp = np.clip(tmp, -1, 1)
B = np.arccos(tmp)
C = np.pi - (A+B)
return A,B,CÖrnek olarak \(b,c\) kenarları \(a\)’ya göre uzun olan bir üçgen kullanalım, bu üçgende tabii ki \(A\) açısı diğerlerine göre küçük olmalıdır,
A,B,C = tri_angles(20,80,80)
print (A,B,C)0.2506556623361308 1.4454684956268313 1.445468495626831np.rad2deg(A)Out[1]: 14.361511562916563İspat için alttaki üçgeni referans alalım [5],
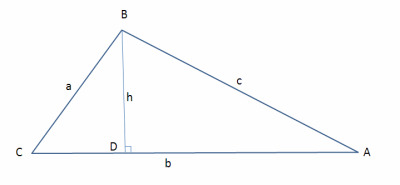
Üstteki figürde bir dik üçgen \(BCD\) var. Kosinüs tanımına göre
\[ \cos C = \frac{CD}{a} \]
Ya da
\[ CD = a \cos C \]
Bu değeri \(b\) kenarından çıkartırsak, alttakini elde ederiz,
\[ DA = b - a \cos C \]
Yine \(BCD\) üçgenine bakalım, sinüs tanımına göre,
\[ \sin C = \frac{BD}{a} \]
Ya da
\[ BD = a \sin C \]
Şimdi \(ADB\) üçgeni üzerinen Pitagor Teorisini uygularsak ve o hesap için şimdiye kadar bulduğumuz büyüklükleri kullanırsak,
\[ c^2 = BD^2 + DA^2 \]
Üstte \(BD,DA\) için önceden bulduğumuz değerleri koyalım,
\[ c^2 = (a \sin C)^2 + (b - a \cos C)^2 \]
Kare çarpımını yaparak parantezleri açalım,
\[ c^2 = a^2 \sin^2 C + b^2 - 2ab\cos C + a^2 \cos^2 C \]
Tekrar duzenleyelim,
\[ c^2 = a^2 \sin^2 C + a^2 \cos^2 C + b^2 - 2ab \cos C \]
\(a^2\) terimini disari cekelim,
\[ c^2 = a^2 (\sin^2 C + \cos^2 C) + b^2 - 2ab\cos C \]
Parantez içindeki büyüklüğün 1 olduğunu biliyoruz, o zaman
\[ c^2 = a^2 + b^2 - 2ab\cos C \]
\[ \cos C = \frac{a^2 + b^2 - c^2}{2ab} \]
\[ C = cos^{-1} \left( \frac{a^2 + b^2 - c^2}{2ab} \right) \]
Diğer iki açı formülünün ispatı benzer şekilde yapılabilir.
Radyan
Acıları 0 ile 360 arasında temsil edebildiğimiz gibi radyan (radian) olarak ta temsil edebiliriz. Zaten radyan yaklaşımı çemberle alakalı her türlü hesaba doğal olarak dahildir; bir çemberin çevresi \(2 \pi \cdot r\) olarak hesaplanır, ki \(r\) yarıçaptır, buradaki \(2 \pi\) tüm 360 dereceye tekabül eden radyan açısı olarak görülebilir, yani 360 = 6.28.. diye gider, \(\pi\) sayısının iki katıdır.
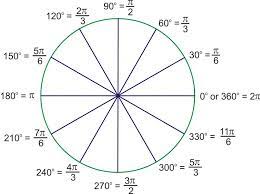
Buradan hareketle çemberin ufak bir parçasının uzunluğunu radyan açısı ile bulabiliriz, eğer tüm çevre \(2 \pi r\) ise 45 derecelik parçanın uzunluğu nedir? \(\pi / 4 \cdot r\) tabii ki, yani \(\pi / 4\) radyan açısı ile yarıçap çarpılır.
Zaten tüm yaygın kullanılan matematiksel yazılım paketleri de
trigonometrik fonksiyonları için radyan açı olarak parametre beklerler.
Mesela numpy ile,
np.cos(6.28)Out[1]: 0.9999949269133752np.sin(6.28)Out[1]: -0.0031853017931379904Tam sıfır çıkmadı sıfıra yakın çünkü \(\pi\)’nin iki katını noktadan sonra iki basamağa yuvarladık.
np.sin(6.28318)Out[1]: -5.307179586686775e-06Aynı paketlerde dereceden radyana geçiş için fonksiyonlar vardır,
np.deg2rad(180)Out[1]: 3.141592653589793Eğer küçük açılardan bahsediyorsak ufak çember parçalarını hayal ederek bazı yaklaşıklamalar mümkündür [2]. Alttaki ufak \(\theta\) açısına bakalım,
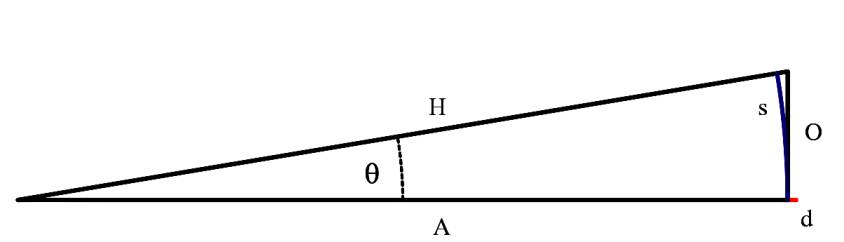
Görülen çemberin ufak \(s\) parçası radyan ile \(s = A \theta\) olur, değil mi? Buradan ilerlersek ve çok ufak açılar için \(s \approx O\) ve \(H \approx A\) olmasından hareket ederek bazı ilginç sonuçlara varacağız.
Tanjant karşı bölü komşudur, resimde bu \(O / A\), fakat küçük açı durumunda \(O \approx s\), o zaman,
\[ \tan \theta = \frac{O}{A} \approx \frac{s}{A} = \frac{A\theta}{A} = \theta \]
Yani ufak açı sözkonusu ise \(\tan \theta \approx \theta\)! Böyle durumlarda sadece karşı bölü komşu bölüm hesabı yaparak radyan üzerinden \(\theta\) açısını bulabiliyoruz!
Devam edelim, sinüs hesabı karşı bölü hipotenüs, yani \(O / H\), küçük açı durumunda \(H \approx A\), o zaman
\[ \sin \theta = \frac{O}{H} \approx \frac{O}{A} \approx \frac{s}{A} = \frac{A\theta}{A} = \theta \]
Aynı \(\theta\) sonucuna eriştik.
Üstteki geometrik bir yaklaşımdı, Calculus kullanan bir diğer ispat altta bulunabilir.
Diğer Trigonometrik Eşitlikler
Toplam Formülleri
Açı toplama eşitliklerine bakalım. Bu eşitlikler
\[ \cos(A+B) = \cos A \cos B - \sin A \sin B \]
\[ \sin(A+B) = \sin A \cos B + \cos A \sin B \]
Ispata gelelim. Önce Euler eşitliği,
\[ e^{i\theta} = \cos\theta + i\sin\theta \]
Şimdi diyelim ki \(\theta = A+B\), o zaman [1],
\[ \cos(A+B) + i\sin(A+B) = e^i(A+B) \]
\[ = e^{iA} \cdot e^{iB} \]
\[ = (\cos A + i\sin A) (\cos B + i\sin B) \]
Çarpımı açarsak,
\[ = \cos A \cos B + i\cos A \sin B + i\sin A \cos B - \sin A \sin B \]
Dikkat son terimdeki eksi işaretin sebebi \(i \cdot i = -1\) olması çünkü hayali sayı \(i\)’nin tanımı \(i = \sqrt{-1}\).
Bir gruplama yapalım,
\[ = \cos A \cos B - \sin A \sin B + i (\cos A \sin B + \sin A \cos B ) \]
Buraya nereden geldiğimizi hatırlayalım, üstteki ifadenin \(\cos(A+B) + i\sin(A+B)\)’e eşit olması gerekir. Eşitlik ne demektir? Üstteki formülün reel kısmını \(\cos(A+B) + i\sin(A+B)\)’in reel kısmına, hayali kısmının yine aynı formülün hayali kısmı ile eşit olması demektir. O zaman ispat tamamlanmış oldu.
Tanjant için ilginç bir eşitlik,
\[ \tan (\alpha + \beta) = \frac{\tan\alpha + \tan\beta}{1 - \tan\alpha \tan\beta} \]
Çıkartma için benzer bir eşitlik geçerli,
\[ \tan (\alpha - \beta) = \frac{\tan\alpha - \tan\beta}{1 + \tan\alpha \tan\beta} \]
İspat [3] oldukça mekanik şekilde yapılabilir, direk tanjant tanımı ile başlayalım,
\[ \tan A = \frac{\sin A}{\cos A} \]
\[ \tan (\alpha + \beta) = \frac{\sin (\alpha + \beta)}{\cos (\alpha + \beta)} \]
Esitligin sag tarafi su sekilde genisletilebilir,
\[ \frac{\sin (\alpha + \beta)}{\cos (\alpha + \beta)} = \frac{\sin\alpha \cos\beta + \cos\alpha + \cos\alpha \sin\beta } {\cos\alpha \cos\beta - \sin\alpha - \sin\alpha \sin\beta} \]
Sağ tarafı \((\cos\alpha)(\cos\beta)\) ile bölelim, bu bize
\[ \dfrac{\dfrac{\sin\alpha\cos\beta}{\cos\alpha\cos\beta} + \dfrac{\cos\alpha\sin\beta}{\cos\alpha\cos\beta}} {\dfrac{\cos\alpha\cos\beta}{\cos\alpha\cos\beta} - \dfrac{\sin\alpha\sin\beta}{\cos\alpha\cos\beta}} \]
\[ = \frac{\tan\alpha + \tan\beta}{1 - \tan\alpha \tan\beta} \]
Böylece ilk eşitliğe erişmiş olduk, eski işaretli versiyona aynı yaklaşımla erişilebilir.
Çift Açı Formülleri
İspatladığımız
\[ \cos(A+B) = \cos A \cos B - \sin A \sin B \]
formülünde eğer \(B\) yerine \(A\) kullanırsak, o zaman \(2A\) elde ederiz, bunun açılımı neye eşit olur?
\[ \cos(A+B) = \cos(A+A) = \cos(2A) = \cos A \cos A - \sin A \sin A \]
\[ \cos(2A) = \cos A^2 - \sin A^2 \]
Ayni teknigi \(\sin(A+B)\) uzerinde uygularsak,
\[ \sin(A+B) = \sin(A+A) = \sin(2A) = \sin A \cos A + \cos A \sin A \]
Bu iki terim birbirinin aynısı, o zaman
\[ \sin(2A) = 2\sin A \cos A \]
Şimdiye kadar elde ettiğimiz
\[ \cos^2\theta + \sin^2\theta = 1, \quad \cos^2\theta - \sin^2\theta = \cos2\theta \]
formüllerinden ek eşitlikler türetmek mümkün. Eğer iki formülü toplarsak
\[ 2\cos^2\theta = 1 + \cos2\theta \]
eğer 2’inciyi 1’inciden çıkartırsak,
\[ 2\sin^2\theta = 1 - \cos2\theta \]
elde ederiz.
Küçük Açı Yaklaşıklaması (Small Angle Approximation)
Bazı fizik kitaplarında ve eğer ufak açılar sözkonusu ise bazen \(\sin\theta \approx \theta\) geçişi yapıldığını görüyoruz. Bu nereden geliyor?
Sinüs fonksiyonu üzerinde Maclaurin açılımı [2] yaparsak (yani sıfır etrafında Taylor açılımı),
\[ \sin\theta = \theta - \frac{\theta^3}{3!} + \frac{\theta^5}{5!} - \frac{\theta^7}{7!} + ... \]
Radyan olarak düşünürsek eğer \(\theta\) çok küçük, yani sıfıra yakın ise küpü alınan çok küçük değer daha da küçülecektir, o zaman ikinci terim dahil olmak üzere tüm diğer terimler yok sayılabilir,
\[ \sin\theta \approx \theta \]
Dahası da var! Çok ufak bir açının kosinüsü 1’e yakındır, ve tanjant sinüs bölü kosinüs olduğu için bölen 1 iptal edilir, geriye kalanlar,
\[ \tan\theta \approx \sin\theta \approx \theta \]
Faydalı olabilir!
Sayısal olarak kontrol edelim,
theta = 0.01
print (np.sin(theta))
print (np.tan(theta))0.009999833334166664
0.010000333346667207Üstteki numaralar bazen ilginç şekillerde karşımıza çıkabilir, mesela bir eğrinin eğiminin ne olduğunu hatırlarsak,
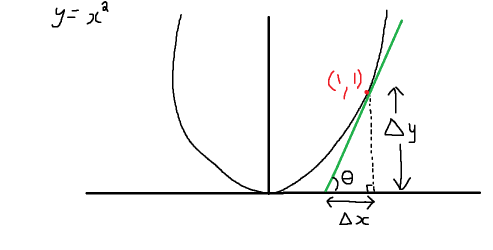
Eğim \(\Delta y / \Delta x\), ki bu yaklaşık olarak türevin ta kendisi değil midir, yani \(dy / dx\)? Evet. Aynı şekilde üstte gördüklerimizden hareketle bu eğime \(\tan\theta\) diyebiliriz, ve ufak açılar sözkonusu ise \(\tan\theta \approx \theta \approx dy / dx\)!
Ufak sayılar sözkonusu ise \(\arctan\) için benzer bir durum geçerli, ufak değerlerde \(\arctan(x) \approx x\). İspat için \(\arctan\) Taylor açılımına bakalım,
\[ \arctan(x) = x - \frac{x^3}{3} + \frac{x^5}{5} + ... \]
Ufak \(x\) var ise bu durumda \(x^3\) ve \(x^5\) gibi üstel hesaplar daha da ufalacaktır, yaklaşık olarak sıfıra yakın kabul edilebilirler. O zaman üstteki formülde kesirli terimler yok sayılabilir, sonuç olarak \(\arctan(x) \approx x\).
Ters Trigonometrik Formüller (Inverse Trigonometric Functions)
\(\cos x\) için \(\cos^{-1} x\) ya da \(\arccos x\) ile gösterilen ters trigonometrik formüldür. \(\sin x\) ve \(\tan x\) için aynı şekilde.
Bu ters fonksiyonların türevi nasıl alınır? \(\theta = \tan^{-1}x\) örneğinde görelim. Elde etmek istediğimiz \(d\theta/dx\).
Eğer
\[ \tan^{-1}x = \theta\]
ise, o zaman
\[ \tan\theta = x \]
\(x\)’i aslında \(\theta\)’ya bağlı bir \(x(\theta)\) fonksiyonu olarak görebiliriz. Eğer iki tarafın \(\theta\)’ya göre türevini alırsak
\[ \frac{dx}{d\theta} = \sec^{2}\theta \]
Bizim istediğimiz bunun tersi, o zaman bölümü tersine çevirelim
\[ \frac{d\theta}{dx} = \frac{1}{\sec^{2}\theta} \]
Pitagor Eşitliklerinden bildiğimize göre
\[ \sec^{2}\theta = \tan^{2}\theta + 1 \]
Yerine geçirelim
\[ \frac{d\theta}{dx} = \frac{1}{\tan^{2}\theta + 1} \]
İlk başta tanımladığımıza göre \(\tan\theta = x\), bunu da üstte yerine koyalım
\[ = \frac{1}{x^2 + 1} \]
Kaynaklar
[1] Blackpenredpen, Angle Sum formula, proof by complex number, https://www.youtube.com/watch?v=OcXqF8l2crI
[2] Wikipedia, Small angle approximation, https://en.wikipedia.org/wiki/Small-angle_approximation
[3] Math Guide, https://www.mathguide.com/lessons2/SDAT.html
[4] Law of Cosines Calculator, https://www.calculatorsoup.com/calculators/geometry-plane/triangle-law-of-cosines.php
[5] Proof of the Law of Cosines, https://www.mathopenref.com/lawofcosinesproof.html