Yaklaşıksal SVD ile Tavsiye Sistemleri
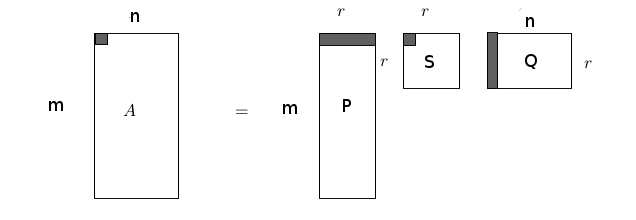
Geçmiş verilere bakarak bir kullanıcının hiç seyretmediği bir filme nasıl not vereceğini tahmin etmek ünlü Netflix yarışmasının konusuydu. Önceki bir yazı [14]'te benzer bir veri seti Movielens üzerinde SVD uygulayarak önce boyut azaltmıştık, azaltılmış boyut üzerinden yeni (o film için notu bilinmeyen) bir kullanıcının diğer mevcut kullanıcılara mesafesini hesaplamış, ve böylece beğeni açısından en çok benzediği diğer kullanıcıyı bulmuştuk (birkaç tane de bulunabilir). Bu kullanıcının bir film için verdiği notu yeni kullanıcı için tahmin olarak baz almıştık. SVD'yi kullanmanın bir yöntemi daha var, Netflix yarışmasında kullanılan [1] bir yaklaşım şöyle; alttaki SVD ayrıştırmasına bakalım,
1'inci kullanıcının 1'inci filme verdiği not üstte köyü gösterilen satırların çarpımı ile oluyor, eğer ufak harfler ve kullanıcı (user) için $u$, film için $i$ indisini, ve $q,p$ vektörlerini $Q,P$ matrislerinin sırasıyla kolon ve satırlarını göstermek için kullanırsak, ayrıştırma sonrası beğeni değeri (önemli bir kısmı daha doğrusu) $q_i^Tp_u$ çarpımındadır. Çarpım içinde $S$'ten gelecek eşsiz değeri (singular value) ne olacak? Şimdi formülasyonda bir değişiklik düşünelim, bu değerin çarpım dışına alındığını hayal edelim; bu değerin kabaca birkaç toplamın sonucuna dönüştüğünü düşünelim. Matematiksel olarak imkansız değil. Bu toplam terimleri, toplam oldukları için, bir baz seviyesi tanımlayabilirler. Bir kullanıcının ne kadar yanlı (bias) not verdiğini, ya da bir filmin nasıl not almaya meyıllı olduğunu modelleyebilirler (ki bu da bir yanlılık ölçüsü). Ayrıca tüm filmlere verilen notların yanlılığı da ayrı bir terim olarak gösterilebilir. Tüm bunları bir araya koyarsak, bir beğeni notunu tahmin edecek formül şöyle gösterilebilir,
$$ \hat{r}_{ui} = \mu + b_i + b_u + q_i^Tp_u $$
$\mu$ bir skalar, tüm filmlere verilen ortalamayı gösteriyor, ki tüm beğenilerin sayısal ortalaması üzerinden basit bir şekilde hızla hesaplanabilir. $\hat{r}_{ui}$'ya bir tahmin dedik çünkü modelimizdeki vektörlerin değerlerini bulduktan sonra (eğitim verisiyle bu hesabı yapacağız) modeli kullanarak gerçek not $r_{ui}$ için bir tahmin olarak kullanılacak.
Yanlılık hakkında bazı örnekler vermek gerekirse, diyelim ki kullanıcı Bob not verirken yüksek seviyede oy vermeye meyıllı. Bu durumda bu kullanıcının ortalama hatta düşük oy vermesi onun bir filmden hakikaten hiç hoşlanmadığını sinyalleyebilir. Ya da bir film genellikle ortalama oy almaktadır, bu durumda ona çok iyi not veren bir kişinin bu filmi çok beğendiği ortaya çıkar. Modeldeki yanlılık parametreleri bu durumu saptayabilirler. Eğer verimizde / gerçek dünyada yanlılık var ise, modelin bu bilgiyi kullanması onun başarısını arttıracaktır.
Eğitim
Eğitim için ne yapmalı? Minimize edeceğimiz bir hedef fonksiyonu kuralım, ki çoğunlukla bu karesi alınmış hata ile olur. Mesela gerçek not $r_{ui}$ değerinden tahmin notu $\hat{r}_{ui}$'yi çıkartıp karesini alabiliriz. Bu işlemi tüm $u,i$'ler için yaparak sonuçları toplarız, ve bu toplamı minimize etmeye uğraşabiliriz. Yani
$$ \min_{b\star,q\star,p\star} \sum_{u,i} (r_{ui} - \hat{r}_{ui})^2 + \lambda (b_i^2 + b_u^2 + ||q_i||^2 + ||p_u||^2) $$
$$ = \min_{b\star,q\star,p\star} \sum_{u,i} (r_{ui} - \mu - b_i - b_u - q_i^Tp_u)^2 + \lambda (b_i^2 + b_u^2 + ||q_i||^2 + ||p_u||^2) $$
Kısaltma olarak $e_{ui}$ tanımlayalım, bu faydalı olabilir, formüldeki ilk parantez içindeki kısımda kullanmak üzere,
$$ e_{ui} := r_{ui} - \hat{r}_{ui} $$
$\lambda$ ile çarpılan bölüm regülarizasyon için. İstatistik, yapay öğrenimde modelimizin aşırı uygunluk (överfitting) yapmasını engellemek için regülarizasyon kullanılır, bunun için istediğimiz değişkenlerin fazla büyümesini cezalandırırız, üstteki minimizasyon modelinde bu ceza için tüm değerlerin büyüklüğünü (magnitude) hesapladık -skalar değerlerin karesini, vektör değerlerinin kare norm'unu alarak- ve bu büyüklükleri bizim dışarıdan tanımlayacağımız bir sabitle çarpımı üzerinden minimizasyon problemine direk dahil ettik. Böylece bu büyüklükler azaltılma hedefinin parçası haline geldiler. Yani hem $e_{ui}^2$ hem de hatayı oluşturan değerlerin kendileri minimize edilecek. Bu minimizasyon sırasında bazı değişkenlerin sıfıra inip o $u,i$ için tamamen etkisiz hale gelmesi bile mümkündür (ki bu bize o parametrenin önemsiz olduğunu sinyalleyebileceği için faydalıdır).
Rasgele Gradyan İnişi (Stochastic Gradient Descent -SGD-)
Modeli nasıl minimize ederiz? Bu model konveks (convex) değil, ki konvekslik bilindiği gibi fonksiyonun düzgün bir çukur gibi olduğu problemlerdir. Böyle çukur fonksiyonlarında herhangi bir noktadan başlarsınız, gradyanı hesaplarsınız, ve bu gradyan hep optimal iniş noktasını (daha doğrusu tersini) gösterir, ve yolda giderken takılıp kalabileceğiniz yerel minimumlar mevcut değildir, ve sonunda çukur dibine ulaşılır. Bizim problemimizde $q_i^Tp_u$ var, bu değişkenlerin ikisi de bilinmiyor, ve bu çarpımın karesi alındığı için genel karesellliği (quadratic) kaybetmiş oluyoruz. Fakat yine de SGD bu problemi çözebiliyor. Bunun sebeplerini, SGD SVD'nin hikayesiyle beraber yazının sonunda bulanabilir.
SGD için gradyanlar lazım, her değişken için minimizasyon toplamı içindeki kısmın (bu kısma $E$ diyelim) ayrı ayrı kısmı türevini almak lazım. Mesela $b_u$ için
$$ \frac{\partial E}{\partial b_u} = -2e_{ui} + 2 \lambda b_u $$
Gradyan her zaman en yüksek çıkışı gösterir, o zaman hesapsal algoritma onun tersi yönüne gitmelidir. Bu gidişin adım büyüklüğünü kontrol etmek için dışarıdan bizim belirlediğimiz bir $\gamma$ sabiti ile çarpım yapabiliriz, ve bir numara daha, sabit 2 değerlerinin $\gamma$ içinde eritilebileceğini farzederek onları sileriz. Yani adım $\gamma(e_{ui} - \lambda b_u)$ haline geldi. Bir döngü içinde eski $b_u$ bulunacak, gördüğümüz yönde adım atılacak, yani adım önceki değere toplanacak, ve yeni değer elde edilecek. Diğer değişkenler için türev alıp benzer işlemleri yaparsak, sonuç şöyle,
$$ b_u \leftarrow b_u + \gamma (e_{ui} - \lambda \cdot b_u) $$
$$ b_i \leftarrow b_i + \gamma (e_{ui} - \lambda \cdot b_i) $$
$$ q_i \leftarrow q_i + \gamma (e_{ui}\cdot p_u - \lambda \cdot q_i) $$
$$ p_u \leftarrow p_u + \gamma (e_{ui}\cdot q_i - \lambda \cdot p_u) $$
Her değişken için başlangıç noktası rasgele olarak seçilebilir, hatta seçilmelidir; İnternet'te bu konu hakkında "efendim tüm değerleri 0.1 değeri yapsanız olur" gibi yorumlar okuyabilirsiniz, bu durumda $q_i,p_u$ değişkenlerinin tüm hücreleri aynı değerde kalır! Yani $q_3$ mesela, tamamen 0.6 değerine sahip olur, ki bu istenen bir şey olmaz. $\gamma,\lambda$ sabitleri için en iyi değerler deneme/ yanılma ya da çapraz sağlama (crossvalidation) ile bulunabilir, biz bu örnekte deneme / yanılma yöntemini seçtik.
Rasgelelik, aynen Lojistik Regresyon örneğinde olduğu gibi verinin rasgeliliğinden geliyor, her veri noktasını teker teker sırayla işliyoruz aslında fakat bu "sıranın" rasgele olduğunu farzettiğimiz için özyineli algoritmamız rasgelelik elde ediyor. Python kodu altta, eğitim için kod sadece bir kere verinin üzerinden geçiyor. Başa dönüp birkaç kere (hatta yüzlerce) veriyi işleyenler de olabiliyor.
from numpy.linalg import linalg as la
import numpy as np
import random, pandas as pd
def create_training_test(df,collim=2,rowlim=200):
test_data = []
df_train = df.copy()
for u in range(df.shape[0]):
row = df.ix[u]; idxs = row.index[row.notnull()]
if len(idxs) > collim:
i = random.choice(idxs); val = df.ix[u,i]
test_data.append([u,i,val])
df_train.ix[u,i] = np.nan
if len(test_data) > rowlim: break
return df_train, test_data
def ssvd(df_train,k):
lam = 0.02 # regularizasyon
gamma = 0.01 # adim katsayisi
m,n = df_train.shape
b_u = np.random.uniform(0, 0.1, size=m)
b_i = np.random.uniform(0, 0.1, size=n)
p_u = np.random.rand(m,k)
q_i = np.random.rand(k, n)
r_ui = np.array(df_train)
for u in range(m):
row = df_train.ix[u]; idxs = row.index[row.notnull()]
for i in idxs:
i = int(i)
r_ui_hat = np.dot(q_i[:,i].T,p_u[u,:])
e_ui = r_ui[u,i] - r_ui_hat
q_i[:,i] = q_i[:,i] + gamma * (e_ui*p_u[u,:].T - lam*q_i[:,i])
p_u[u,:] = p_u[u,:] + gamma * (e_ui*q_i[:,i].T - lam*p_u[u,:])
return q_i,p_u
Kodun önemli bir özelliği şudur, boş yani nan değeri içeren notlar eğitim
sırasında atlanır. SGD seyrek verilerle de işleyebilen bir eğitim yöntemidir. Bu
durumda verinin seyrekliği (sparsıty) bizim için çok faydalı, çünkü o veri
noktalarına bakılmayacak, row.notnüll() ile boş olmayan öğelerin indis
değerlerini alıyoruz. Bilindiği üzere Movielens, Netflix verileri oldukça
seyrektir, kullanıcı binlerce film içinden onlar, yüzler bağlamında not verimi
yapar, geri kalan değerler boştur.
Pratikte Atlanabilecek Formüller
Üstteki formülasyon içinde genel, film ve kullanıcı yanlılıkları formül içinde belirtilmiştir. Pratikte sayısal hesap açısından bu yanlılıkları daha SVD başlamadan önce veriden çıkartmak, ve yanlılılıkları rasgele güncelleme mantığından çıkartmak daha iyi sonuç veriyor. Bu çıkartma şöyle yapılır; önce film ortalamaları hesaplanır, her kullanıcı için o kullanıcının o film ortalamasına olan farkı (offset) hesaplanır ve bu fark eğitim sırasında not olarak kullanılır. Böylece SVD tüm yanlılıklardan arınmış bir fark hesabı ile çalışır sadece, ve sayısal olarak bu daha avantajlıdır. Yoksa ilk atılan adımda fark çok büyük olacağı için bu fark gradyan inişinin yönününü ağırlıklı olarak belirleyecektir, ve bu ilk atılan adım hesabın geri kalanına aşırı baskın çıkabilecektir (dominate). Zaten SVD'nin kuzeni olan PCA'den de bildiğimiz gibi, bu yöntem ortalamadan arındırılmış (demeaned) farklarla iş yapıyor.
Niye Azar Azar (Incremental) Hesap?
Madem $U,S,V$ hesabı yapar gibi $q_i,p_u$ hesaplıyoruz, niye bu hesabı adım adım yapıyoruz?
Bu sorunun cevabı azar azar hesap yaparken hafızaya sadece o satırı alarak daha az bellek kullanmamız. Milyarlarca boyut ve milyarlarca satır işliyor olsaydık bu matrisin tamamını hafızaya almamız mümkün olmazdı.
Ayrıca olmayan verileri atlamak bu SVD hesabını bir "veri tamamlama problemi" haline getiriyor, piyasadaki neredeyse diğer tüm kütüphaneler olmayan veriyi sıfır olarak kabul eder. Bu farklı bir problemdir. Bu diğer SVD yöntemlerinde her ne kadar olan veriyi ortalasak ve sıfır değerleri sıfır averajla aynı anlama gelmeye başlasa bile, yine de olmayan veriyi sıfır kabul etmek onu atlamaktan farklıdır [12].
Basit bir örnek
import pandas as pd
import ssvd
d = np.array(
[[ 5., 5., 3., nan, 5., 5.],
[ 5., nan, 4., nan, 4., 4.],
[ nan, 3., nan, 5., 4., 5.],
[ 5., 4., 3., 3., 5., 5.],
[ 5., 5., nan, nan, nan, 5.]
])
data = pd.DataFrame (d, columns=['0','1','2','3','4','5'],
index=['Ben','Tom','John','Fred','Bob'])
avg_movies_data = data.mean(axis=0)
data_user_offset = data.apply(lambda x: x-avg_movies_data, axis=1)
q_i,p_u = ssvd.ssvd(data_user_offset,k=3)
print 'q_i',q_i
print 'p_u',p_u
u = 4; i = 2 # Bob icin tahmin yapalim
r_ui_hat = np.dot(q_i[:,i].T,p_u[u,:]) + avg_movies_data.ix[i] + \
np.nan_to_num(data_user_offset.ix[u,i])
print r_ui_hat
q_i [[ 0.77564986 0.1768796 0.56224297 0.42870962 0.94723452 0.55772707]
[ 0.74100171 0.18146607 0.07704434 0.17631144 0.48868432 0.90470742]
[ 0.70541948 0.28729857 0.091619 0.46184649 0.64498754 0.27410096]]
p_u [[ 0.41549541 0.59784095 0.45227968]
[ 0.7756159 0.1197948 0.2921504 ]
[ 0.82274016 0.58432802 0.46501307]
[ 0.1877425 0.21364635 0.1924456 ]
[ 0.80554597 0.59254732 0.9775562 ]]
3.92146103113
Not: Artımsal SVD için bir diğer teknik için bkz. Ders 29.
Test Etmek
Test verisi oluşturmak için eğitim verisinde rasgele olarak bazı notları seçtik,
bunları bir kenara kaydederek onların ana matris içindeki değerini sildik
(yerine nan koyarak), ve bir kısmı silinmiş yeni bir eğitim matrisi
yarattık, create_training_test işlevinde bu görülebilir. Bu işlevde her
kullanıcıdan sadece bir tane not verisi alıyoruz, ve bunu sadece belli bir
sayıda, collim kadar, not vermiş kullanıcılar için yapıyoruz, ki böylece
az sayıda not vermiş kullanıcıların verisini azaltmamış oluyoruz. Ayrıca belli
miktarda, rowlim kadar test noktası elde edince iş bitti kabul
ediyoruz. Test verisi yaratmak için \%80-\%20 gibi bir ayrım yapmadık, yani
eğitim verişindeki tüm kullanıcıları ve onların neredeyse tüm verisini eğitim
için kullanıyoruz.
Movielens verisine gelelim, [14] yazısındaki movielens_prep.py ile
gerekli eğitim dosyası üretildiğini farzederek,
import pandas as pd, os
df = pd.read_csv("%s/Downloads/movielens.csv" % os.environ['HOME'] ,sep=';')
print df.shape
df = df.ix[:,1:3700] # id kolonunu atla,
df.columns = range(3699) # kolon degerlerini tekrar indisle
print df.shape
(6040, 3731)
(6040, 3699)
avg_movies = df.mean(axis=0)
df_user_offset = df.apply(lambda x: x-avg_movies, axis=1)
print df.ix[6,5], avg_movies.ix[5], df_user_offset.ix[6,5]
4.0 3.87872340426 0.121276595745
Eğitim ve test verisi yaratıyoruz,
import ssvd
df_train, test_data = ssvd.create_training_test(df_user_offset,rowlim=500,collim=300)
print len(test_data)
501
q_i,p_u = ssvd.ssvd(df_train,k=8)
Test
rmse = 0; n = 0
for u,i,real in test_data:
r_ui_hat = np.dot(q_i[:,i].T,p_u[u,:])
rmse += (real-r_ui_hat)**2
n += 1
print "rmse", np.sqrt(rmse / n)
rmse 0.936136196897
Sonuç fena değil.
Formülasyonun Hikayesi
SGD SVD'nin hikayesi şöyle. Yıl 2009, Netflix Yarışması [11] katılımcılarından Simon Funk (gerçek adı Brandyn Webb) SGD SVD yaklaşımını kodlayıp veri üzerinde işletince birden bire sıralamada ilk 3'e fırlar; Webb artık çok ünlü olan blog yazısında [1] yaklaşımı detayıyla paylaşıp forum'da haberini verince bu haber tam bir bomba etkisi yaratır. Pek çok kişi yaklaşımı kopyalar, hatta kazanan BellKor ürününde Webb'in SVD yaklaşımının kullanıldığı biliniyor.
Bu metotun keşfi hangi basamaklardan geçti? Beni meraklandıran minimizasyon formülasyonun konveks olmamasıydı -- genellikle optimizasyon problemlerinde konveksliğin mevdudiyeti aranır, çünkü bu durumda sonuca yaklaşmak (convergence) için bir garanti elde edilir. Bu durumda konvekslik yoktu. "O zaman Webb nasıl rahat bir şekilde SGD kullanabildi?" sorusunun cevabını merak ediyorduk yani. Biraz araştırınca Bottou ve LeCunn gibi araştırmacıların yazılarına ulaştık [4]. Onlara göre konvekslik olmaması yapay öğrenim araştırmacılarını korkutmamalı, eğer sayısal (empiriçally) işleyen bir algoritma var ise, teorik ispat gelene kadar bu metotun kullanılmasında sakınca yoktur.
Fakat böyle buluşlarda yine de bazı garantiler temel alınmış olabilir, araştırmacı tamamen balıklama atlayış yapmaz. Webb'in kendisine bu soruları sorduk ve bize buluşun hangi seviyelerden geçtiğini anlattı. Geriye sarıyoruz, Webb Netflix'den çok önce yapay sınır ağlarını araştırmaktadır, ve Sanger, Oja'nın [5,6] yayınlarını baz alarak kurduğu bir YSA için bir çözüm bulduğunu farkeder. Sayısal çözümde özdeğer/vektör bulmaya yarayan Üstel Metotun (power method) bir şeklini kullanmıştır, ki Sanger'in Genel Hebbian Algorıtmasının (GHA) üstel metot ile bağlantıları var, ve bu GHA yayınında "eğitilince" özdeğer/vektör ve PCA hesabı yapabilen bir YSA'dan bahsediliyor. Daha önemlisi GHA 1 olasılıkla (yani kesin) bu sonuçlara erişebiliyor.
Daha sonra Webb bu çözümü arkadaşı Gorrell ile tartışırken Gorrell ona problem formülasyonunun SVD olarak görülebileceğini söyler. Bilindiği gibi özdeğer/vektör hesabı ile SVD yakın akraba sayılır. İkili bu bağlamda birkaç yayın da yaparlar. Daha sonra Netflix yarışması başladığında Webb çözüm için gradyan baz alarak SGD kullanabileceğini farkediyor, ki SGD ile üstel metot arasında teorik bağlantı var [7]. Ve sonuç olarak SGD SVD metotu ortaya çıkıyor.
Tabii ki "SGD SVD ne kadar SVD sayılır?" gibi bir soru sorulabilir. Evet, regülarizasyon bazı gayrı lineerlikleri probleme sokar, zaten bu çözümü "yaklaşıksal" yapan kısım da budur. Fakat belli şartlarda, regülarizasyon olmasa çözüm tam SVD olacaktır. Bu buluşun püf noktası bu bilgide, ve üstteki teorik benzerliklerde, onları biliyor olmakta yatıyor. Eğer bunlar biliniyor ise, ve sağlam lineer cebir bilgisi ile gerektiği zaman onları ne kadar esnetebileceğimizi biliriz. Konu hakkındaki daha fazla detay [10]'da bulunabilir.
Tavsiye
movies = pd.read_csv("../../stat/stat_pandas_ratings/movies.dat",\
sep='::',names=['idx','movie','type'])
def eval_user(u):
res = {}
for i in range(df_user_offset.shape[1]):
r_ui_hat = np.dot(q_i[:,i].T,p_u[u,:])
res[i] = float(r_ui_hat) + avg_movies.ix[i] + df_user_offset.ix[u,i]
res = sorted(res.items(), key=lambda x:x[1], reverse=True)
print "\n\nTavsiyeler\n\n"
for j,(si,sm) in enumerate(res):
print movies[movies['idx'] == si]['movie']
if j == 10: break
print "\n\nMevcut Filmler\n\n"
row = df.ix[u]
idxs = row.index[row.notnull()]
for j,idx in enumerate(idxs):
print movies[movies['idx'] == idx]['movie'], row[idx]
if j == 10: break
eval_user(300)
eval_user(2900)
Tavsiyeler
3441 Frequency (2000)
Name: movie, dtype: object
105 Muppet Treasure Island (1996)
Name: movie, dtype: object
Series([], dtype: object)
2 Grumpier Old Men (1995)
Name: movie, dtype: object
4 Father of the Bride Part II (1995)
Name: movie, dtype: object
1 Jumanji (1995)
Name: movie, dtype: object
3 Waiting to Exhale (1995)
Name: movie, dtype: object
0 Toy Story (1995)
Name: movie, dtype: object
5 Heat (1995)
Name: movie, dtype: object
6 Sabrina (1995)
Name: movie, dtype: object
7 Tom and Huck (1995)
Name: movie, dtype: object
Mevcut Filmler
Series([], dtype: object) 5.0
0 Toy Story (1995)
Name: movie, dtype: object 3.0
1 Jumanji (1995)
Name: movie, dtype: object 4.0
3 Waiting to Exhale (1995)
Name: movie, dtype: object 3.0
4 Father of the Bride Part II (1995)
Name: movie, dtype: object 5.0
9 GoldenEye (1995)
Name: movie, dtype: object 4.0
15 Casino (1995)
Name: movie, dtype: object 4.0
19 Money Train (1995)
Name: movie, dtype: object 5.0
20 Get Shorty (1995)
Name: movie, dtype: object 3.0
23 Powder (1995)
Name: movie, dtype: object 4.0
30 Dangerous Minds (1995)
Name: movie, dtype: object 5.0
Tavsiyeler
Series([], dtype: object)
0 Toy Story (1995)
Name: movie, dtype: object
1 Jumanji (1995)
Name: movie, dtype: object
2 Grumpier Old Men (1995)
Name: movie, dtype: object
3 Waiting to Exhale (1995)
Name: movie, dtype: object
4 Father of the Bride Part II (1995)
Name: movie, dtype: object
5 Heat (1995)
Name: movie, dtype: object
6 Sabrina (1995)
Name: movie, dtype: object
7 Tom and Huck (1995)
Name: movie, dtype: object
8 Sudden Death (1995)
Name: movie, dtype: object
9 GoldenEye (1995)
Name: movie, dtype: object
Mevcut Filmler
19 Money Train (1995)
Name: movie, dtype: object 4.0
23 Powder (1995)
Name: movie, dtype: object 4.0
37 It Takes Two (1995)
Name: movie, dtype: object 3.0
45 How to Make an American Quilt (1995)
Name: movie, dtype: object 5.0
48 When Night Is Falling (1995)
Name: movie, dtype: object 5.0
66 Two Bits (1995)
Name: movie, dtype: object 5.0
78 Juror, The (1996)
Name: movie, dtype: object 4.0
104 Nobody Loves Me (Keiner liebt mich) (1994)
Name: movie, dtype: object 5.0
118 Race the Sun (1996)
Name: movie, dtype: object 4.0
134 From the Journals of Jean Seberg (1995)
Name: movie, dtype: object 2.0
142 Brothers McMullen, The (1995)
Name: movie, dtype: object 3.0
Numba ve Funk SVD
Eğer Numba [13] kullanırsak, SVD kodunu çok daha hızlı işletebiliriz. Ayrıca
Funk'ın kodlaması (ki alttaki kodu onu temel alacak) biraz daha ilginç, mesela
en dış döngü özellikler (feature) geziyor, onun içindeki birkaç yüz kez yine
kendi içinde olan tahmin/hata hesabını yapıyor, tüm veri seti üzerinde. Bunun
için Movielens 100k verisi lazım, ardından data_m100k.py ile veri
yaratılır,
# Requires Movielens 100k data
from scipy.io import mmread, mmwrite
import numpy as np, time, sys
from numba import jit
import os
def create_user_feature_matrix(review_matrix, NUM_FEATURES):
num_users = review_matrix.shape[0]
user_feature_matrix = 1./NUM_FEATURES * \
np.random.randn(NUM_FEATURES, num_users).astype(np.float32)
return user_feature_matrix
def create_movie_feature_matrix(review_matrix, NUM_FEATURES):
num_movies = review_matrix.shape[1]
movie_feature_matrix = 1./NUM_FEATURES * \
np.random.randn(NUM_FEATURES, num_movies).astype(np.float32)
return movie_feature_matrix
@jit(nopython=True)
def predict_rating(user_id, movie_id, user_feature_matrix, movie_feature_matrix):
rating = 1.
for f in range(user_feature_matrix.shape[0]):
rating += \
user_feature_matrix[f, user_id] * \
movie_feature_matrix[f, movie_id]
if rating > 5: rating = 5
elif rating < 1: rating = 1
return rating
@jit(nopython=True)
def sgd_inner(feature, A_row, A_col, A_data,
user_feature_matrix, movie_feature_matrix,
NUM_FEATURES):
K = 0.015
LEARNING_RATE = 0.001
squared_error = 0
for k in range(len(A_data)):
user_id = A_row[k]
movie_id = A_col[k]
rating = A_data[k]
p = predict_rating(user_id,
movie_id,
user_feature_matrix,
movie_feature_matrix)
err = rating - p
squared_error += err ** 2
user_feature_value = user_feature_matrix[feature, user_id]
movie_feature_value = movie_feature_matrix[feature, movie_id]
user_feature_matrix[feature, user_id] += \
LEARNING_RATE * (err * movie_feature_value - K * user_feature_value)
movie_feature_matrix[feature, movie_id] += \
LEARNING_RATE * (err * user_feature_value - K * movie_feature_value)
return squared_error
def calculate_features(A_row, A_col, A_data,
user_feature_matrix, movie_feature_matrix,
NUM_FEATURES):
MIN_IMPROVEMENT = 0.0001
MIN_ITERATIONS = 200
rmse = 0
last_rmse = 0
print len(A_data)
num_ratings = len(A_data)
for feature in xrange(NUM_FEATURES):
iter = 0
while (iter < MIN_ITERATIONS) or (rmse < last_rmse - MIN_IMPROVEMENT):
last_rmse = rmse
squared_error = sgd_inner(feature, A_row, A_col, A_data,
user_feature_matrix, movie_feature_matrix,
NUM_FEATURES)
rmse = (squared_error / num_ratings)
iter += 1
print ('Squared error = %f' % squared_error)
print ('RMSE = %f' % rmse)
print ('Feature = %d' % feature)
return last_rmse
def main():
LAMBDA = 0.02
NUM_FEATURES = 30
A = mmread('%s/Downloads/A_m100k_train' % os.environ['HOME'])
user_feature_matrix = create_user_feature_matrix(A, NUM_FEATURES)
movie_feature_matrix = create_movie_feature_matrix(A, NUM_FEATURES)
A = A.tocoo()
rmse = calculate_features(A.row, A.col, A.data,
user_feature_matrix, movie_feature_matrix,
NUM_FEATURES )
print 'rmse', rmse
np.savetxt("/tmp/user_feature_matrix2.dat", user_feature_matrix)
np.savetxt("/tmp/movie_feature_matrix2.dat", movie_feature_matrix)
if __name__ == "__main__":
main()
Üstteki script'i işlettikten sonra bazı tavsiyeleri gösterebiliriz,
import pandas as pd, os
items_file = '%s/Downloads/ml-100k/u.item' % os.environ['HOME']
item_df = pd.read_csv(items_file, sep='|',header=None)
item_df['idx'] = item_df[0] - 1
item_df = item_df.set_index('idx')
from scipy.io import mmread, mmwrite
import numpy as np, time, sys, os
import funk2, pandas as pd
user_feature_matrix = np.loadtxt("/tmp/user_feature_matrix2.dat")
movie_feature_matrix = np.loadtxt("/tmp/movie_feature_matrix2.dat")
preds = []
user_id = 110
for movie_id in range(1682):
pred = funk2.predict_rating(user_id, movie_id, user_feature_matrix, movie_feature_matrix)
preds.append([movie_id, pred])
preds_df = pd.DataFrame(preds,columns=['movie','score'])
preds_df.sort_index(by='score',ascending=False,inplace=True)
preds_df['movie_name'] = item_df[1]
print preds_df.head(10)
movie score movie_name
1448 1448 4.600873 Pather Panchali (1955)
407 407 4.538450 Close Shave, A (1995)
168 168 4.424078 Wrong Trousers, The (1993)
482 482 4.406603 Casablanca (1942)
99 99 4.402690 Fargo (1996)
11 11 4.362673 Usual Suspects, The (1995)
319 319 4.323309 Paradise Lost: The Child Murders at Robin Hood...
49 49 4.315158 Star Wars (1977)
113 113 4.308009 Wallace & Gromit: The Best of Aardman Animatio...
172 172 4.288836 Princess Bride, The (1987)
Bu kişinin seyrettiği ve en çok beğendiği filmler altta
A = mmread('%s/Downloads/A_m100k_train' % os.environ['HOME']).tocsc()
movies = A[user_id,:].nonzero()[1]
ratings = A[user_id,A[user_id,:].nonzero()[1]]
ratings = np.ravel(ratings.todense())
likes_df = pd.DataFrame()
likes_df['movie'] = movies; likes_df['rating'] = ratings
likes_df = likes_df.set_index('movie')
likes_df.sort_index(by='rating',ascending=False,inplace=True)
likes_df['movie_name'] = item_df[1]
print likes_df.head(10)
rating movie_name
movie
301 5 L.A. Confidential (1997)
314 5 Apt Pupil (1998)
257 4 Contact (1997)
285 4 English Patient, The (1996)
303 4 Fly Away Home (1996)
310 4 Wings of the Dove, The (1997)
353 4 Wedding Singer, The (1998)
302 3 Ulee's Gold (1997)
320 3 Mother (1996)
304 2 Ice Storm, The (1997)
Kaynaklar
[1] Funk, Netflix Update: Try This at Home, http://sifter.org/~simon/journal/20061211.html
[2] Koren, Bell, Recommender Systems Handbook, http://www.cs.bme.hu/nagyadat/Recommender_systems_handbook.pdf
[3] Koren, MATRIX FACTORIZATION TECHNIQUES FOR RECOMMENDER SYSTEMS , https://datajobs.com/data-science-repo/Recommender-Systems-%5BNetflix%5D.pdf
[4] LeCun, Who is Afraid of Non-Convex Loss Functions?, http://videolectures.net/eml07_lecun_wia
[5] Sanger, Optimal Unsupervised Learning in a Single-Layer Linear Feedforward Neural Network , http://courses.cs.washington.edu/courses/cse528/09sp/sanger_pca_nn.pdf %
[6] Oja, A Simplified Neuron Model as a Principal Component Analyzer, http://users.ics.aalto.fi/oja/Oja1982.pdf
[7] Cotter, Stochastic Optimization for Machine Learning, http://arxiv.org/pdf/1308.3509
[8] Touchette, Introduction to Numerical Computing, http://www.maths.qmul.ac.uk/~wj/MTH5110/notes/MAS235_lecturenotes1.pdf
[10] Stack Exchange, Gradient Descent on Non-Convex Function Works But How?, http://math.stackexchange.com/questions/649701/gradient-descent-on-non-convex-function-works-but-how
[11] Netflix, Netflix Prize, http://www.netflixprize.com
[12] Gleich, SVD on the Netflix matrix, https://dgleich.wordpress.com/2013/10/19/svd-on-the-netflix-matrix
[13] Bayramlı, Numba, LLVM, ve SVD, https://burakbayramli.github.io/dersblog/sk/2014/09/numba-llvm-ve-svd.html
[14] Bayramlı, Istatistik, SVD, Toplu Tavsiye
Yukarı