Satırsal \(A^TA\)
[5]’te tek makinalı ortamda matris çarpımının nasıl yapılacağını, ve nasıl görülecebileğini anlattık. Satır bakış açısı, kolon bakış açısı işlendi. Peki parallel bir ortamda hangi matematik bizi ilgilendirmeli? Mesela \(A^TA\)’yi ele alalım. Bu çarpım oldukça önemli çünkü başka sonuçlar için de kullanılabiliyor, Eşsiz Değer Ayrıştırması (Singular Value Decomposition -SVD-) bunlardan biri.
Büyük Veri ve paralel işlem bağlamında \(A^TA\)’nin önemli şurada; eğer \(A\) matrisi “uzun boylu ve zayıf’’ ise, yani çok miktarda satırı ama az miktarda kolonu var ise, \(m \times d\) diyelim, \(A^TA\) çarpımı bize \(d \times d\) boyutunda ufak bir matris verir. Eğer SVD hesabını bu matris üzerinden yapabilirsek, işimizi kolaylaştırmış oluruz.
Satırsal olarak \(A^TA\) hesabı yapmak için satır satır gezerken her satırın kendisi ile dışsal çarpımını (outer product) alıp sonuçları toplamak yeterli [9]. İşlemi daha sözel tarif eden bir açıklama [3]’de bulunabilir.
\(A^TA\) ve SVD
\(A^TA\) açılımını yapalım [7], bir \(A\) için SVD ayrıştırması
\[ A = U \Sigma V^T \]
olduğuna göre
\[ A^TA = (U \Sigma V^T)^T U \Sigma V^T \]
olacaktır, devam edersek,
\[ = V \Sigma U^T U \Sigma V^T \]
\(U^T U = I\) olduğu için geri kalanlar
\[ A^TA = V \Sigma^2 V^T \]
Peki eşitliğin sağından \(V\)’yi nasıl çıkartırız? Bir dikgen matris çarpı köşegen bir matris çarpı o dikgen matrisin devriği bize bir şeyi hatırlatıyor mu? Evet, bu bir özdeğer / özvektör hesabına benziyor, [2]’de görüldüğü gibi \(A=S\Lambda S^{-1}\) ayrıştırması da var (birimdik matrislerde tersi alma işleminin devrik ile aynı şey olduğunu unutmayalım). O zaman \(A^TA\)’nin öz hesabını yaparsak oradaki özvektör bize \(V\) matrisini verecektir.
\(U\)’yi elde etmek için basit matris çarpımları yeterli,
\[ A = U \Sigma V^T \to U = A V \Sigma^{-1} \]
Yani \(V\) elde edildikten sonra onunla \(A\)’yi çarpıyoruz, sonra \(\Sigma^{-1}\) ile. \(A\) ne kadar büyük olursa olsun onu bir vektör \(V\) ile çarpmak hızlı işler, \(\Sigma\) ise köşegen, seyrek bir matristir, onun çarpımı da basittir.
Bu işlemlerin paralel versiyonları için [8, 6] kaynaklarına bakılabilir.
SVD ve öz hesapların benzerliği için alttaki koda bakılabilir,
import numpy.linalg as lin
import pandas as pd
k = 7 # izdusum uzayinin boyutlari
df = pd.read_csv("../linear_app10rndsvd/w1.dat",sep=';',header=None)
A = np.array(df)[:,1:]
print (A.shape)(71, 30)ATA = np.dot(A.T,A)
eval,evec = lin.eig(ATA)
u,s,v = lin.svd(A)
print (evec.shape)
print (v.shape)(30, 30)
(30, 30)Matrisler birbirine değersel olarak ne kadar yakın, kontrol edelim,
print ( np.mean(np.abs(evec) - np.abs(v.T)))0.005230468666628483
-2.7259159635502234e-13Fark çok ufak (abs ile mutlak değer kullandık çünkü
bazen tüm bir kolon diğerinin eksi hali olabiliyor).
SVD İçin QR
QR ile SVD yapmak mumkundur. QR ayrıştırması [4] kolonların hepsi bilindiği gibi birbirine dik (orthogonal) birim vektörler olan bir \(Q\) matrisi ve üst üçgensel (upper triangular) bir \(R\) matrisi oluşturur. Ayrıştırmanın \(A^TA\) ile bağlantısı nedir? Eğer \(A\) yerine onun ayrıştırmasını \(QR\) koyarsak,
\[ C = A^TA = (QR)^T (QR) = R^T Q^T QR \]
Tum \(Q\) vektorleri birbirine dik, ve birim vektorler ise, \(Q^T Q\) birim matrisi \(I\) olur. O zaman
\[ C = R^T Q^T QR = R^T R \]
Yani
\[ C = R^TR \]
Peki \(A^TA\) hesaplayıp (böylece \(R^TR\)’yi elde edince) onun içinden \(R\)’yi nasıl çekip çıkartırız? Şimdi Cholesky ayrıştırması kullanmanın zamanı. Cholesky ayrıştırması (herhangi bir simetrik pozitif kesin \(C\) matrisi üzerinde)
\[C = LL^T\]
olarak bilinir, yani bir matris alt üçgensel (lower triangular -ki L harfi oradan geliyor-) \(L\) matrisine ve onun devriği olan üst üçgensel \(L^T\)’nin çarpımına ayrıştırılır. Elimizde \(R^TR\) var, ve ona benzer \(LL^T\) var, \(R\) bilindiği gibi üst üçgensel, \(L\) alt üçgensel, \(L^T\) ve \(R\) birbirine eşit demek ki. Yani \(A^TA\) üzerinde sayısal hesap kütüphenimzin Cholesky çağrısı kullanmak bize \(QR\)’in \(R\)’sini verir.
Şu anda akla şu soru gelebilir: madem kütüphane çağrısı yaptık, niye \(A\) üzerinde kütüphenimizin \(QR\) çağrısını kullanmıyoruz?
Cevap Büyük Veri argümanında saklı. Bu ortamda uğraşılan verilerde \(A\) matrisi \(m \times n\) boyutlarındadır, ve \(m\) milyonlar, hatta milyarlarca satır olabilir. Şimdilik \(m >> n\) olduğunu farzedelim, yani \(m\), \(n\)’den “çok, çok büyük”, yani “boyut kolonlarının”, ki \(n\), sayısı binler ya da onbinlerde. Bu gayet tipik bir senaryo aslında, ölçüm noktaları (boyutlar) var, ama çok fazla değil, diğer yandan o ölçümler için milyonlarca veri noktası toplanmış. Tipik bir aşırı belirtilmiş (överdetermined) sistem - ki en az kareler (least squares) gibi yaklaşımların temel aldığı sistemler bunlardır, eldeki denklem sayısından daha fazla ölçüm noktası vardır. Bu arada en az karelerden bahsettik, \(QR\)’in kullanıldığı alanlardan biri en az karelerin çözümüdür.
Argümana devam ediyoruz, kütüphane qr çağrısını \(A\) üzerinde yaparsak, \(m \times n\) gibi devasa bir matris
üzerinde işlem yapmak gerekir. Ama \(A^TA\) üzerinde işlem (Cholesky) yaparsak,
ki bu çarpımın boyutu \(n \times m \cdot m
\times n = n \times n\), yani çok daha ufak bir matristir. \(A^TA\)’in işlem bedeli çok ufak, birazdan
anlatacağımız yöntem sayesinde bu bedel \(O(m)\).
SVD
Simdi \(QR\) sonuçlarını kullanarak SVD hesaplamaya gelelim. SVD bize ne verir?
\[ A = U \Sigma V^T \]
\(U\) ve \(V^T\) dikgen (orthogonal) matrislerdir, \(\Sigma\) sadece köşegeni boyunca değerleri olan bir matristir. Daha fazla detay için bkz [4]. Şimdi \(A = QR\) yerine koyalım,
\[ QR = U \Sigma V^T \]
\[ R = Q^T U \Sigma V^T \]
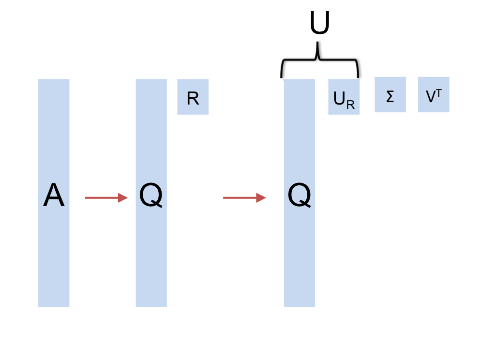
Bu son formüledeki \(Q^TU\) ibaresi, iki dikgen matrisin çarpımıdır. Lineer Cebir kurallarına göre iki dikgen matrisin çarpımı bir diğer ortogonal matristir. Bu yeni dikgen matrise \(U_R\) adı verelim, o zaman
\[ R = U_R \Sigma V^T \]
Bu son formül bize bir şeyler söylüyor. \(R\)’nin SVD üzerinden ayrıştırılabileceğini söylüyor ve bu ayrıştırma sonrası ele geçen \(U_R,V^T\) ve \(\Sigma\) köşegen matrisleridir! Bu çok önemli bir sonuç. Bu ayrıştırmanın sonucu \(A\)’nin ki ile birbirine çok benziyor, tek fark \(U\) ile \(U_R\). Bu iki matris arasındaki geçiş şöyle:
\[ U_R = Q^T U \]
\[ U = QU_R \]

Bu demektir ki eğer \(R\) üzerinde
kütüphanemizin svd çağrısını kullanırsak (ki \(R\) nispeten ufak olduğu için bu ucuz olur)
ele geçen \(U_R\)’i alıp, \(Q\) ile çarparsak, \(A\) ayrıştırmasının \(U\)’sunu elde ederiz! \(Q\) ile paralel yapılabilir.
Tekrar paylaşmak gerekirse paralelleştirme teknikleri [6,8] yazılarında.
Kaynaklar
[1] Benson, A., Tall-and-skinny Matrix Computations in MapReduce
[2] Bayramlı, Lineer Cebir Ders 22, https://burakbayramli.github.io/dersblog/linear/linear_22/ders_22.html
[3] Bayramlı, https://burakbayramli.github.io/dersblog/sk/2022/11/paralel-lineer-cebir.html
[4] Bayramlı, Lineer Cebir, Ders 29
[5] Bayramlı, Lineer Cebir, Matris Çarpımı, Ders 1
[7] Zadeh, CME 323: Distributed Algorithms and Optimization, Lecture 17, https://stanford.edu/~rezab/classes/cme323/S17/
[8] Bayramlı, Paralel Lineer Cebir, https://burakbayramli.github.io/dersblog/sk/2022/11/paralel-lineer-cebir.html
[9] Gundersen, Matrix Multiplication as the Sum of Outer Products, https://gregorygundersen.com/blog/2020/07/17/matmul/