Ders 12

Bu ders daha çok uygulama ağırlıklı olacak. Şimdiye kadar farketmişsinizdir, ne zaman bir örnek matris bulmak gerekse, onu hemen uydurarak ortaya çıkartıyorum, bunun hakkında biraz kendimi suçlu hissediyorum, çünkü gerçek Lineer Cebir'de çoğunlukla bir gerçek dünya probleminden gelen matrisler vardır, hocanın kafasından attığı şeyler değillerdir. Bu matrislerin bir yapısı olur çoğunlukla, ve bu matrislerle haşır neşir olan kişiler o yapıyı bilirler, vs.

Mesela geçen hafta sonu İleri Kimya konusunda araştırma yapan profosörler ile beraberdim. Bu hocalar satır azaltılmış (row reduced) matrislerle uğraşıyorlar, mesela her tür molekülden kaç tanesinin bir reaksiyona girdiğini takip ediyorlar, ve satır azaltması yaparak bir reaksiyonun daha net resmini görebiliyorlar. Sonra, önümüzdeki hafta Mathworks şirketinde bir doğum günü partisine gideceğim, bu şirket Route 9 üzerinde, ki bilindiği gibi Mathworks'ün ürünü Matlab'dir [ki 1999 yılında hocanın dersinde Matlab referans ediliyordu, ama biz artık Python kullanıyoruz, zaten kendisi de başka bir derste bu tavsiyede bulunmuştu]. Matlab çok başarılı bir ürün tabii ki. Ayrıca bir konferans ta olacak, konusu Lineer Cebir'in nasıl kullanıldığı. İşte bu sebeplerden dolayı suçluluk hissediyorum :) Her yer uygulama!

Bana göre Uygulamalı Matematik (Applied Math) alanındaki en önemli uygulama çizitler ve ağlar (graphs and networks) konusudur. Bir çizit ortaya çıkartacağım şimdi, ve onu temsil eden matrisi yazacağım; daha önce değindiğim gibi mesela Web sitelerinin çiziti çok ilginç olmalı. Ya da tüm telefonların bağlantılarının çiziti, ya da tüm insanların arasındaki ilişkilerin çiziti.

Basit bir örnek,

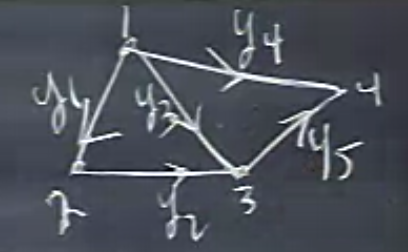
İşte bir çizit, 4 düğümü 5 kenarı var. Bu çiziti temsil eden matriste o zaman 5 satır olacak, ve 4 tane kolon olacak, $m=5,n=4$. Bu arada her kenar için bir +/- olarak betimlenecek bir yön de vereyim [ki bu bilgi de önceden bilinecek bir şey, uygulamadan gelecek yani, bizim uydurduğumuz bir şey olmayacak], ve kenarlara bir sayı vereyim [altta yeşil ile işaretli].

Birazdan aklımdaki bir uygulamayla alakalı olarak, potensiyel, akım gibi kelimeler de kullanacağım, ki aklımdaki uygulama bir elektriksel bir devre yapısı. Tabii bu sadece bir uygulama, pek çok diğer örnek olabilir, hidrolik bir ağ yapısı olabilir mesela, suyun akışının da inceliyor olabilirdim, ya da petrolün borulardan akışını.. İlla bir şeyin akıyor olması da gerekmez, bir statik yapıyı, mesela bir köprünün yapısını da bir çizit ile inceliyor olabilirdim.

Neyse, şimdilik potansiyel ve akımlara bakalım. Üstteki resimdeki çizite tekabül eden bir geliş (incidence) matrisi yazacağım, her satır bir kenar olacak şekilde,

$$ A = \left[\begin{array}{rrrr} -1 & 1 & 0 & 0 \\ 0 & -1 & 1 & 0 \\ -1 & 0 & 1 & 0 \\ -1 & 0 & 0 & 1 \\ 0 & 0 & -1 & 1 \end{array}\right] $$

Kenar 1 düğüm 1'den çıkıyor (onun için o değer -1) ve düğüm 2'ye giriyor (onun için değeri +1).

İlk 3 satıra bakarsak ki bu satırlar çizitin sol tarafındaki ufak üçgeni gösteriyor, orada bir döngü (loop) var, bir çizitte kaç tane döngü olduğu ve onların nerede olduğu önemli bir konu.

Döngüler hakkında ilginç bir bilgi, eğer 1,2,3 bir döngü oluşturuyorsa, burada matrissel ilginç bir soru şudur: döngü içindeki 1,2,3 satırlarına tekabül eden satırlar birbirinden bağımsız mıdır? Çıplak gözle bunu anlayabilir miyiz? Evet, ve bu satırlar bağımlı, 1. ve 2. satır toplanınca 3. satır ortaya çıkıyor. Bu durum aslında bizim için bir işaret olmalı, lineer olarak bağımlı olan satırlar döngü olduğuna dair bir işarettir.

Bu matris hakkında ilginç bazı diğer gözlemler; her kenar tek bir yerden çıkıp tek bir yere girdiğine göre her satır için iki öğe dolu olacak, geri kalan hücreler sıfır olacak. Bu sebeple görüldüğü gibi matris seyrek (sparse); matris dolululuğu $2m$. İşte daha önce belirttiğim yapı durumu buydu, gerçek uygulamalarda karşımıza çıkan matrislerde bir yapı vardır, işte burada görüyoruz; her satırda sadece iki hücre dolu, gerisi sıfır.

Ya sıfır uzayı? Ondan önce, bu matrisin sıfır uzayını sormak ne demektir? Matrisin kolonları hakkında bir soru sormak demektir, eğer o kolonlar bağımsız ise, matrisin sıfır uzayında sadece sıfır vektörü vardır. Çünkü sıfır uzayı bize kolonları nasıl birleştirip sıfır sonucunu elde edeceğimizi söyler, eğer bunu yapamıyorsak, bağımlılık yok demektir.

$Ax=0$'i çözelim, üstteki matrisin yanına çarpan olarak $x$ vektörünü ekleyeyim,

$$ Ax = \left[\begin{array}{rrrr} -1 & 1 & 0 & 0 \\ 0 & -1 & 1 & 0 \\ -1 & 0 & 1 & 0 \\ -1 & 0 & 0 & 1 \\ 0 & 0 & -1 & 1 \end{array}\right] \left[\begin{array}{r} x_1 \\ x_2 \\ x_3 \\ x_4 \end{array}\right] = 0 $$

Bu çarpımı açarsak,

$$ Ax = \left[\begin{array}{r} x_2 - x_1 \\ x_3 - x_2 \\ x_3 - x_1 \\ x_4 - x_1 \\ x_4 - x_3 \end{array}\right] = \left[\begin{array}{r} 0 \\ 0 \\ 0 \\ 0 \\ 0 \end{array}\right] $$

Bu çarpımın ne yaptığına dikkat edelim; her kenarın iki ucundaki düğümünün farkını hesaplıyor, yani potansiyel farkını. Terminolojiye yeni bir kelime ekledik şimdi, daha iyi tanımlamak gerekirse $x=x_1,x_2,x_3,x_4$ düğümlerin potansiyeli olsun. Hesabı yaparsak, tabii ki ilk akla gelen tüm $x$ öğelerinin sıfır olması, o zaman sıfır sonucu gelir: sıfır vektörü sıfır uzayının parçasıdır. Fakat daha fazlası da var. Matrise çıplak gözle bakarak bile hemen bir tane bulabiliriz, mesela tüm $x$'lere 1 değerini versem, o zaman üstteki hesapta yine sıfır elde ederim değil mi? Yani tüm potansiyeller eşitse, onların farkı sıfır olur.

Sıfır uzayında başka ne var? Sıfır uzayının bazı nedir? İçinde tamamen 1 olan vektör bu bazdır. Tüm sıfır uzayı $x = c \left[\begin{array}{cccc} 1 & 1 & 1 & 1 \end{array}\right]^T$, yani sabitle çarpılan tamamen 1 içeren vektör. Bu 4 boyutlu uzayda sonsuza giden bir çizgiyi temsil edecek.

Buradaki fiziksel anlam nedir? Eğer farkları temsil ettiysek ve bu farkların sıfır olduğu durumu çözüyorsak, $x_1,..,x_4$'un hep aynı değerde olması şaşırtıcı olmamalı, çünkü birbirleri ile aynı değerlerin farkı sıfır olur. Elektriksel devre olarak düşünürsek, tüm potansiyeller aynı ise, yani potansiyel farkları sıfır ise akım yoktur.

Diğer yönden, eğer tüm devrede akımı bulmak istiyorsak, bir düğüm noktası (üstteki gibi bir örnekte) / bir potansiyel "topraklanır (grounding)", yani sıfır değerine eşitlemek gerekir, böylece tüm matris çözülebilir hale gelir, yani amaç hem fiziksel hem matematiksel, geri kalan bağımsız değişkenler üzerinden çözüm ve devre üzerinde akım mümkün olur.

$A$ matrisinin kertesi nedir? Kaç bağımsız kolon var? 3 tane. Matristen hangi 3 kolonu seçersek bu kolonlar birbirinden bağımsız olacaktır.

$A^T$'nin sıfır uzayını düşünelim; çünkü $A^Ty=0$ denklemi herhalde uygulamalı matematiğin en önemli denklemlerinden biridir, bunu bulalım. Ondan önce $dim(N(A^T))$ nedir? $A^T$'nin boyutu $4 \times 5$. Kerte $m-r$, yani 5-3=2. Güzel, boyutu biliyorum, şimdi bu sıfır uzayının kendisini bulmak istiyorum. Matris,

$$ \left[\begin{array}{rrrrr} -1 & 0 & -1 & -1 & 0 \\ 1 & -1 & 0 & 0 & 0 \\ 0 & 1 & 1 & 0 & -1 \\ 0 & 0 & 0 & 1 & 1 \end{array}\right] \left[\begin{array}{r} y_1 \\ y_2 \\ y_3 \\ y_4 \\ y_5 \end{array}\right] = \left[\begin{array}{r} 0 \\ 0 \\ 0 \\ 0 \end{array}\right] $$

Daha ilerlemeden önce büyük resmi göstermek istiyorum,

İlk başta elimizde $x$ değerleri var bunlar potansiyeller (potential at nodes). $A$ ile çarpınca farkları elde ediyoruz (potential differences). Ayrıca öyle bir matris $C$ vardır ki bu matris potansiyel farkları kenarlardaki akımlar (currents on edges) ile ilintilendirir, ve bu akımlar ve potansiyel farkları arasındaki ilişki Ohm Kanunu'nun ta kendisidir. Ohm Kanunu potansiyel farkınının akım çarpı bir sayı (ki o sayı $C$ içinde) olduğunu söylemez mi? Bu sayı tabii ki elektriksel direnç.

Resimdeki son adım Kirchoff'un Akım Kanunu (Kirchoff's CL), yani birazdan $Ay=0$ çözdüğüm zaman Kirchoff Kanununu çözmüş olacağım.

Evet, şimdi $Ay=0$'a dönelim, bu matris içindeki çarpımlara denklem olarak bakarsak, mesela ilk satır ne der?

$$ -y_1 - y_3 - y_4 = 0 $$

Eğer çiziti hatırlarsak,

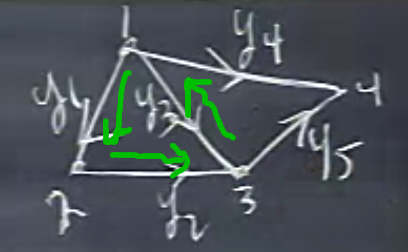
Çizite göre $y_1,y_2,y_3$ "akımları" 1. düğümü terketmekte, 1. düğüme tekabül eden 1. satırdaki tüm $y$ değişkenleri eksi değerde. 2. satır,

$$ y_1 - y_2 = 0$$

1. düğüme bakıyoruz, $y_1$ giriyor (işareti artı), $y_2$ çıkıyor, bir denge var, toplam sıfır. 3. satır?

$$ y_2 + y_3 - y_5 = 0 $$

1. satır

$$ y_4 + y_5 = 0 $$

Bu denklem aslında elektrikte Kirchoff Kanununu ortaya çıkardı, yani bir düğüme giren ve çıkan akımlar birbirine eşit olmalıdır. Diğer yandan potansiyel farklarını gösteren denklem Ohm Kanunu idi. Şimdiye kadar gördüğümüz $A$ ve $A^T$ işlemlerinin direk elektrik konusuna uygulanabilmesi müthiş bir şey!

Lineer cebir sorusuna dönelim şimdi, hangi $y$'ler sıfır uzayı sorusunu çözer (yani Kirchoff kanununu)? Eliminasyona girmek istemiyorum şimdi, bunu yapabiliriz, yapmayı biliyoruz artık, $A^T$ üzerinde azaltılmış basamaklı formu (reduced echelon form) elde ederiz, vs., bunlara girmeden sonucu bulabilir miyim?

Eliminasyon yapsaydım son satır ne olurdu? Tamamen sıfır olurdu. Niye, çünkü kerte 3, o zaman son satır sıfır. Neyse, çizite tekrar dönelim, öyle bir $y$'ler olmalı ki akım bu devrede "birikmeden" sürekli aksın, giren çıkan aynı olsun.

$N(A^T)$'nin bazında kaç vektör vardır? İki tane, çünkü $N(A^T)$ iki boyutlu bir uzaydır o zaman iki vektör yeterlidir.

Çizite göre, bakıyorum, $y_1=1$ olsun mesela, düğüm 1'den 2'ye bir akım. 2'ye giren akım dışarı çıksın, sonra, $y_3$ üzerinden geriye gitsin mesela. Geriye kalan $y_4,y_5$ sıfır olabilir. Bu hem Kirchoff Akım Kanununa hem de sıfır uzayı çözümüyle uyumludur.

İlk çözümü vektör olarak yazalım,$\left[\begin{array}{ccccc}1&1&-1&0&0 \end{array}\right]^T$. Bu vektör ilk döngüdeki akım aslında, o zaman ikinci döngüdeki akım da bir başka çözüme işaret eder, yani $\left[\begin{array} {ccccc}0&0&1&-1&1 \end{array}\right]^T$

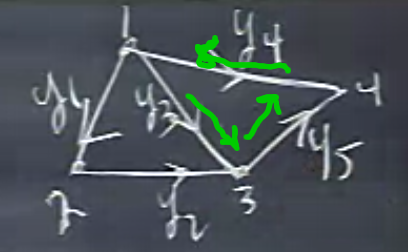
Yani ilk baz vektörü birinci döngü, ikinci baz vektörü ikinci döngü. Bu baz vektörleri birbirinden bağımsızdır, ve elime böylece $N(A^T)$ için için iki çözüm geçer, yani Kirchoff'un Akım Kanununu tatmin eden iki akım.

Bu noktada akla gelebilir, niye 1-2-3-4-1 şeklinde gidebilecek daha büyük bir döngü üzerinden bir akım olmasın? Bu akım $\left[\begin{array} {ccccc}1&1&0&-1&1 \end{array}\right]^T$ olarak temsil edilirdi, bu vektör $A^T$'un sıfır uzayında mıdır? Evet. O zaman niye bazlarımıza üçüncü bir vektör dahil etmiyoruz?

Cevap çünkü bu vektör bağımsız değil. Eğer mevcut bazdaki ilk vektörü ikinciye eklersem üstteki "büyük döngü" vektörünü elde ederim, akımsal olarak düşünürsek birinci ufak döngü akıyor, ikincisi de, $y_3$ üzerinde ikisi karşı karşıya geliyorlar, birbirlerini iptal ediyorlar, ve ortaya büyük döngü akımı çıkıyor.

Gördüğümüz gibi $N(A^T)$'i çözdüm ama aynı zamanda Kirchoff Akım Kanununu da çözmüş oldum, ve bunu ağ yapısını bir matris olarak temsil ederek yapmış oldum.

$A$'nin satır uzayına gelelim. Boyut 3, çünkü kerte 3. Peki üstteki $A^T$ içinde, ilk 3 kolon birbirinden bağımsız mı? Değil (çünkü raslantısal olarak yanyana gelmiş kolonlar -satırlar- bunlar, herhangi 3 kolon bağımsız olacak diye bir kural yok), zaten $N(A^T)$ bazından niye görülüyor, $1,1,-1$ değerleri bir döngü varlığını gösteriyor. Eğer $A^T$ üzerinde eliminasyon yapıyor olsaydım bu sebeple 1. 2. kolonu pivot yapardım, ama 3'u atlayıp 4'u pivot haline getirirdim.

Bu pivot kolonları $y_1,y_2,y_4$ kenarlarına tekabül eder, ve bu durumda hiçbir döngü yoktur. Bağımsızlık çizit bağlamında bu demek, hiç döngü olmama durumu. Elde 3 tane kenar var, bunlar bağımsız, bir tane bile kenar bu listeye eklesem bir döngü ortaya çıkar.

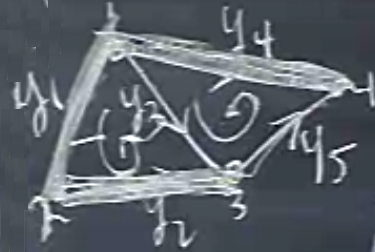
Bu arada, hiç döngüsü olmayan çizite ne denir? Ağaç (tree) denir.

Bu noktada son bir adım daha atalım. Formülü hatırlarsak $dim(N(A^T))=m-r$. Döngü sayısı

$$ \textrm{döngü sayısı} = \textrm{kenar sayısı} - (\textrm{düğüm sayısı} - 1) $$

Eksi 1 gerekti çünkü $r=n-1$ idi hatırlarsak. Biraz değiştirerek yazarsak,

$$ \textrm{düğüm sayısı} - \textrm{kenar sayısı} + \textrm{döngü sayısı} = 1 $$

Üstteki formüle Euler'in Formülü deniyor (yine Euler, bu adam her yerden çıkıyor!). Demek istiyorum ki pür lineer cebir kullanarak Euler'in Formülünü ortaya çıkartmış oldum. Euler'in Formülü matematiğin topoloji alanında çok ünlü bir sonuçtur. Doğrulamak için başka bir çizit görelim şimdi, mesela şimdi kafadan atıyorum, şöyle olsun,

Bu çizitte $\textrm{düğüm sayısı}=5$, $\textrm{kenar sayısı}=7$, $\textrm{döngü sayısı}=3$, üstteki formülde yerine koyarsam, 5-7+3=1. Euler haklı çıktı.

Evet artık büyük resmi tamamlamanın zamanı geldi.

Ders başında gördüğümüz büyük resme döneceğiz. Elde potansiyel farklar var, ki bunlara $e$ diyelim mesela, o zaman $e=Ax$. Akımlar potansiyel farklarla alakalı tabii ki, bu alaka $C$'ler üzerinden, $y=Ce$. Son olarak Kirchoff'un Kanunu $A^Ty=0$ ile akım şiddetleri arasındaki ilişkiyi kuruluyor. Uygulamalı Matematiğin belkemiği budur arkadaşlar, bu denklemlerde gizlidir. Denklemde eksik tek bir şey var, sisteme dışarıdan giriş yok, ama onu da ekleyebilirdim, mesela çizitin (devrenin) iki düğümüne bir pil takarak akım verebilirdim, alttaki gibi [rasgele bir devre çiziyor],

O zaman $Ay=0$ yerine $Ay=f$ derdim.

Şimdi dersi tamamlamadan önce bu üç formülü biraraya koyacağım. Bilinmeyen $x$ ile başladım, onu $A$ ile çarptım bu bana potansiyel farkları verdi, $e=Ax$. Sonra $C$ ile çarptım, ki $C$ içinde Ohm Kanununu için gereken fiziki sabitler var, yani $CAx$ oldu, $y$'yi elde ettim. En son olarak $A^T$ ile çarparım, $A^TCAx$ olur bu da $f$'tır.

$$ A^TCAx = f $$

Formülün tamamı bu. Bu formül Uygulamalı Matematiğin en temel formülüdür. Üç adım uygulayarak bu sonuca geldik, ki son adımda bir denge formülü eklemiş olduk (her problemde, mutlaka bir denge formülü olur). Bu arada, "en temel formül" derken denge (equilibrium) durumları için böyle, çünkü üstteki problemde zaman faktörü yok. Sisteme herşey yerli yerine oturduktan sonra bakıyorum. Resim böyle.

Bitirmeden ufak bir soru: bana $A^TCA$ hakkında ne söyleyebilirsiniz? Ya da $A^TA$ hakkında. Bu matris hakkında ne biliyoruz? Bu matris her zaman simetriktir. Güzel. Şimdilik bu kadar.