
İlk dersimize hoşgeldiniz, ben Gilbert Strang. Lineer cebirin çözmeye çalıştığı en temel problem bir lineer denklem sistemini çözmektir. Bu bağlamda mesela en genel durum “bilinmeyen ve denklem sayısının birbirine eşit olduğu’’ durumdur, ki bu”güzel durum’’ olarak nitelenebilir. Boyut \(n \times n\) olunca bu durumda oluyoruz. Ama diğer durumları da işleyeceğiz.
Dersin kavramlarını anlamak için “satır bakışı’’na başvuracağız, bu durumda her denkleme teker teker bakıyoruz gibi olacak, dersimizde pek çok kez kullanacağımız \(A\) matrisimiz olacak mesela, ve bu matrisin satırların her denklemin değişkenlerinin katsayılarına tekabül edecek.
Kolon bakış açısı belki daha önce görmediğiniz bir açı olacak, bu durumda her kolon ayrı ayrı işlenecek.
Cebirsel bakış açısı ise tüm matrisi, bu durumda \(A\), aynı anda ele alacak.
Güzel durumdan başlayalım; iki bilinmeyen, iki denklem.
\[ 2x - y = 0 \]
\[ -x + 2y = 3 \]
Katsayıları matrise taşıyalım
\[ \left[\begin{array}{cc} 2 & -1 \\ -1 & 2 \end{array}\right] \left[\begin{array}{c} x \\ y \end{array}\right] = \left[\begin{array}{c} 0 \\ 3 \end{array}\right] \]
Soldaki matrise ben çoğunlukla \(A\) derim, sonra içinde bilinmeyenleri taşıyan \(x\) vektörü koyarım, ki bazıları bunu vektör olduğu için köyü renkte \(\mathbf{x}\) olarak ta yazar, ve sonra bir vektör daha, ki buna ben çoğunlukla \(b\) derim, yani sonuç şöyle olur,
\[ A x = b \]
Şimdi satır bakışına başvuralım. Grafik olarak düşünelim, hangi noktalar \(2x - y = 0\) denklemini tatmin eder? Orijin \((0,0)\) noktası bunlardan biri, bir diğeri \(x=1,y=2\). Bunları çizgi ile birleştirip çizgiyi sonsuza uzatırsak,

İkinci denklemi düşünelim, bu denklem orijinden geçmeyecek. \(y\) sıfır olsaydı \(x\) nereden geçerdi..? \(x=-3\) noktasından. \(x=-1\) işe, \(y\) nedir? \(y=1\). Artık ikinci çizgiyi çizebiliriz,

Her iki çizgi \(x=1,y=2\) noktasında buluştu (hoca o noktayı daha önceden tahtaya koymuştu ama buna bir “hazır raslantı’’ diyelim). Bu buluşma noktası her iki denklemi tatmin eden sistemin çözüm noktasıdır.
Kolon bakışına gelelim. Bu bakışa göre
\[ x \left[\begin{array}{r} 2 \\ -1 \end{array}\right] + y \left[\begin{array}{r} -1 \\ 2 \end{array}\right] = \left[\begin{array}{r} 0 \\ 3 \end{array}\right] \]
Bu bakış açısı bize ne söylüyor? Bir anlamda diyor ki “eşitliğin solundaki iki vektörü öyle bir şekilde kombine et ki bu lineer kombinasyon sonucu eşitliğin sağ tarafını versin’’. Bu operasyon, işlem lineer cebir dersinin en temel işlemidir - kolonların lineer kombinasyonu.
Kolonları vektörel olarak çizelim, bilindiği gibi bir vektör orijinden çıkan bir yönü ve büyüklüğü olan bir şeydir. Birinci kolon 2 sağa 1 aşağı gitmeli, ikincisi bir sola 2 yukarı gitmeli. Çizince,
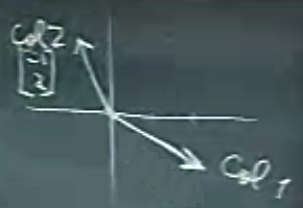
Peki bu vektörleri nasıl “birleştirelim’’ yani hangi katsayılarla çarpıp toplayalım ki \(\left[\begin{array}{rr}3 & 0\end{array}\right]^T\) sonucunu elde edelim? Not: Burada devrik işaretini kullandık çünkü satır vektörünün devriğini alınca kolon vektörü olur, yazarken o şekilde yazdık çünkü başka türlü yazı içine rahat koymak mümkün olmayacaktı.
Neyse, kombine etmek toplamaktır, o zaman ikinci kolonu alıp birinciye ekleyelim, vektör aritmeğitinde toplamak bir vektörü diğerinin bittiği noktadan başlatmak demektir, bir tane (yani katsayı 1 ile) ikinci vektörü birinciye ekleyince
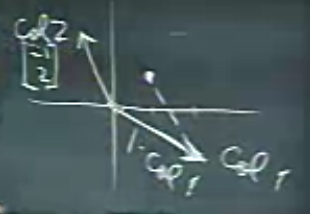
Çözüm noktasına erişemedik daha, 2 tane ekleyince,
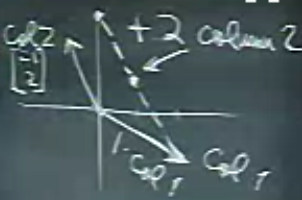
Çözüme eriştik. Çözüm \(y\) ekseni üzerinde 3,0 noktası. Bu noktaya bir lineer kombinasyon yaparak eriştik. “Doğru’’ lineer kombinasyon bize sonucu verdi.
Kendimize şunu soralım: bütün lineer kombinasyonlar bize neyi verirdi? Bu çok önemli bir soru, üzerinde iyi düşünelim, çünkü bu konu tekrar tekrar karşımıza çıkacak. Tüm kombinasyonlar derken tüm \(x,y\)’lerin doğuracağı kombinasyonlar; bu şekilde eşitliğin sağ tarafı ne olursa olsun onu temsil edebilirdik. Yani bu tüm kombinasyonlar tüm bir düzlemi (plane) doldururdu. Bunu bir kenara koyalım, konuyu ileride daha detaylı olarak inceleyeceğiz.
3 Boyut
\[ 2x - y = 0 \]
\[ -2x + y - z = -1 \]
\[ -3y + 4z = 4 \]
Bu sistemi nasıl anlarız? Ne gördük: satır bakışı, kolon bakışı. Matris formuna bakalım,
\[ A = \left[\begin{array}{rrr} 2 & -1 & 0 \\ -1 & 2 & -1 \\ 0 & -3 & 4 \end{array}\right] , b = \left[\begin{array}{r} 0 \\ -1 \\ 4 \end{array}\right] \]
Satır bakışı, üstteki ikinci denklemi alalım, grafiği neye benzer? Orijinden geçen bir şey yok, çünkü \(0,0,0\) bir çözüm olamaz. Çözüm neye benzer? Elimizde bir lineer denklem var ise üç boyutta bu denklemi çözen tüm noktalar bir düzlem (plane) oluştururlar. Hoca diyor ki ben Rembrandt değilim, kabaca bir düzlem çizeceğim,

Birinci denklem neye benzer? \(z\) belirtilmemiş, demek ki herhangi bir şey olabilir, geri kalanlar yine bir düzlem oluştururlar. Mesela alttaki gibi

Bu iki denklemin kesiştiği yer bir çizgidir (line). Bir üçüncü düzlem daha eklenince (üstte yok), tüm üç düzlemin kesiştiği yer bir nokta olur. Bu noktanın ne olduğunu ben kafadan bilmiyorum, ama lineer cebir bu noktayı bulur.
Fakat herhalde görüyorsunuz, satır bakışını zihnimizde canlandırmak biraz zor. Düzlemler, kesişmeler vs düşünmemiz gerekiyor. İki boyutta iki çizgi kesişmesinde problem yoktu, fakat üç boyutta işler biraz karıştı. Dört ya da daha fazla boyutu düşünün!
Kolon bakışı ile
\[ x \left[\begin{array}{r} 2 \\ -1 \\ 0 \end{array}\right] + y \left[\begin{array}{r} -1 \\ 2 \\ -3 \end{array}\right] + z \left[\begin{array}{r} 0 \\ -1 \\ 4 \end{array}\right] = \left[\begin{array}{r} 0 \\ -1 \\ 4 \end{array}\right] \]
Yani eşitliğin sol tarafındaki üç boyutlu vektörlerin hangi kombinasyonu eşitliğin sağındaki üç boyutlu vektörü verir? Çizmeye uğraşalım,
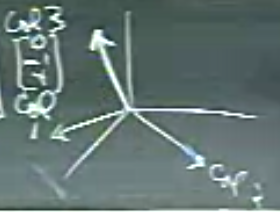
Hocanın hazırladığı örnekte basit bir çözüm var, \(z\) katsayıları ile \(b\) aynı, o zaman \(\left[\begin{array}{ccc}0&0&1\end{array}\right]\) denklemi çözer, \(z=1\) çözüm için yeterli olur, \(z\)’yi alırız, geri kalanları “istemiyoruz’’ onları sıfır yaparız - \(x=0,y=0,z=1\).
Tabii kolon resminin daha düzgün olması her zaman çözümü pat diye görebileceğimiz anlamına gelmiyor, çoğu zaman, hatta yüksek boyutlarda bu da mümkün değil. Eliminasyon yöntemini göreceğiz ileriki derslerde, sistematik olarak herhangi bir boyutta bizim için lineer sistemi çözecek.
Daha geniş resme bir bakalım. Eşitliğin sağ tarafı başka bir şey olsaydı, mesela
\[ x \left[\begin{array}{r} 2 \\ -1 \\ 0 \end{array}\right] + y \left[\begin{array}{r} -1 \\ 2 \\ -3 \end{array}\right] + z \left[\begin{array}{r} 0 \\ -1 \\ 4 \end{array}\right] = \left[\begin{array}{r} 1 \\ 1 \\ 3 \end{array}\right] \]
(Bu sağ tarafı 1. ve 2. kolonları birbirine ekleyerek uydurduk bu arada), çözüm o zaman ne olurdu? Çözüm basit (çünkü kendimiz pişirdik), \(x=1,y=1,z=0\). Üstteki durumda ve satır bakışında tamamen değişik üç tane düzlem elde ederdik. Kolon bakışında hala aynı üç vektörle uğraşırız, sadece onları değişik şekillerde kombine etmemiz gerekir.
Soru: üstteki denklemi herhangi bir \(b\) yani eşitliğin sağ tarafı için çözebilir miyim?
Bu soruyu daha değişik bir şekle sokabilir miyiz, öyle ki soru lineer kombinasyon argümanlarını kullansın.
Soru: üstteki kolonların lineer kombinasyonu bütün 3-boyutlu uzayı doldurur mu?
Cevap, üstteki (gibi bir) matris için “evet’’. Bu matris nasıl bir matris? Bu matris iyi huylu, eşsiz (singular) olmayan, tersi alınabilir (ınvertible) bir matris. Bu tür matrisler için her zaman çözüm var.
Peki iyi huylu olmayan durum nasıl olurdu? Düşünelim, ne yanlış gidebilirdi? Eğer tüm vektörler aynı düzlem üzerinde olsaydılar, o zaman bu vektörlerin her türlü kombinasyonu da aynı düzlem üzerinde olmak zorundadır, o zaman başımız dertte. Mesela 3. kolon 1. ve 2.’nin toplamı olsa (ki bu durumda her üç vektör aynı düzlemdedir), o zaman işler kötü. Niye? Çünkü \(b\) farklı bir düzlemde ise artık hiçbir kombinasyonla oraya erişemem. Eğer \(b\) aynı düzlem üzerinde olsaydı tabii erişilebilirdi, yani bazı \(b\)’ler için çözüm hala var, ama hepsi, çoğunluğu için yok.
İşte eşsiz durum budur, ki bu durumda çoğu \(b\) için çözüm yoktur.
Boyutları arttırdığımızı düşünelim. 9 boyut olsaydı ne olurdu? Bu
kadar boyutu görsel olarak hayal etmek mümkün değil, ama yine aynı
durum, \(Ax=b\) var, bu sefer 9 boyutlu
9 tane kolon var, bunları kombine edip \(b\) elde edeceğiz? Bunu yapmayı
başarabilmemiz tabii ki \(A\)’nin ne
olduğuna bağlıdır. Rasgele bir \(A\)
matrisi üretseydim (ki bu Numpy rand ile basitçe
yapılabilir) size garanti ediyorum bu matris iyi huylu olurdu, eşsiz
olmayan tersi alınabilen vs. ve bu matris ile \(b\)’ye erişebilirdiniz.
Kötü durum kolonlar bağımsız olmadığı zaman. Mesela 7. kolon 5. kolonun tıpatıp aynısı, ki bu durumda 7. kolon sisteme “yeni hiç bir bilgi eklemiyor’’. Bu yüzden bazı \(b\)’lere erişmem imkansız hale geliyor. İyi huylu durumda 9 bağımsız kolonun kombinasyonu tüm 9 boyutlu uzayı doldurabilirdi. Ama bir bağımlı vektör var ise o zaman sadece 9 boyutlu uzayın 8 boyutlu bir alt düzlemini doldurabilirsiniz. Dersimizin ileri noktalarında bu kısıtlı alt uzaylar ile de iş yapmayı öğreneceğiz, yapmamız gerekecek. Şimdilik güzel koşula odaklanalım.
Ayrıca, şimdiye kadar sözel olarak belirttiklerimizi bir de matris formunda, cebiriyle anlatmayı deneyelim. \(Ax=b\) dedik, \(A\) matrisi bir \(x\) vektörü ile çarpılır. Bir vektörü bir matris ile nasıl çarparsınız? Mesela
\[ \left[\begin{array}{rr} 2 & 5 \\ 1 & 3 \end{array}\right] \left[\begin{array}{r} 1 \\ 2 \end{array}\right] \]
Bunu yapmanın iki yolu var. Önce benim en favori yöntemimi söyleyeyim, belki de sürpriz olmayacak, kolonlar kullanarak. Bu durumda, mesela üstteki örnekte, \(A\)’nin 1. kolunundan 1 tane, 2. kolonundan 2 tane alacağım, ve toplayacağım. Yani,
\[ = 1 \left[\begin{array}{r} 2 \\ 1 \end{array}\right] + 2 \left[\begin{array}{r} 5 \\ 3 \end{array}\right] = \left[\begin{array}{r} 12 \\ 7 \end{array}\right] \]
Diğer bir yöntem satır bazlı. Bu durumda \(A\)’nin 1. satırı ile \(x\)’i çarpıyorum, yani noktasal çarpımını alıyorum, ve bu tek bir değer sonucunu verecek, ve tek, skalar değeri alıp sonucun ilk hanesine yazıyorum. Aynı şekilde \(A\)’nin 2. satırını tekrar aynı \(x\) ile noktsal çarpıyorum, ikinci haneye yazıyorum.
Fakat daha önce belirttiğimiz gibi kolon bakışı biraz daha rahat açıklanabilir halde. O zaman şunu söyleyebiliriz: “\(Ax\), \(A\)’nın kolonlarının bir kombinasyonudur’’.
Bir sonraki derste herhangi boyuttaki bir sistem için sistematik olarak eliminasyon yaparak, eğer varsa, bir sonuca ulaşmayı öğreneceğiz. Eğer eliminasyon başarısız olursa bunun üzerinden ne zaman bir sonuç olmadığını görmeyi de öğreneceğiz.
Ekler
Matris Çarpımı
Sırabağımlılık
Matris çarpımı sırabağımlı (commutative) değildir, yani \(AB \ne BA\). Bir örnekte görelim,
\[ \left[\begin{array}{cc} 1&0\\0&0 \end{array}\right] \left[\begin{array}{cc} 0&1\\0&0 \end{array}\right] = \left[\begin{array}{cc} 0&1\\0&0 \end{array}\right] \]
\[ \left[\begin{array}{cc} 0&1\\0&0 \end{array}\right] \left[\begin{array}{cc} 1&0\\0&0 \end{array}\right] = \left[\begin{array}{cc} 0&0\\0&0 \end{array}\right] \]
Satır ve Kolon Bakış Açısı
Matris çarpımının tarifini lise derslerinden hatırlayabiliriz. Sol el sol taraftaki matriste bir satır boyunca, sağ el sağdaki matris üzerinde kolon boyunca öğe öğe hareket ettirilir, ve bu hareket sırasındaki öğeler çarpılıp, o çarpımlar sürekli toplanır. Sol ve sağ elin bir hareketi bittiğinde, ele geçen tek bir sayı vardır, ve o sayı üzerinden geçilen satır \(i\) ve kolon \(j\) için sonuç matrisi, mesela \(C\)’nin, \(i\)’inci satırı ve \(j\)’inci kolonuna yazılır.
Daha basit bir \(Ax\) örneğine bakarsak, yani solda \(A\) ve sağda \(x\) var, çarpım
\[ \left[\begin{array}{ccc} 1 & 1 & 6 \\ 3 & 0 & 1 \\ 1 & 1 & 4 \\ \end{array}\right] \left[\begin{array}{ccc} 2 \\ 5 \\ 0 \\ \end{array}\right] \]
Noktasal Çarpım Bakışı
Bu çarpımı bir kaç şekilde görebiliriz. Eğer üstte tarif edilen gibi gördüysek,
\[ \left[\begin{array}{ccc} 1\cdot 2 + 1\cdot 5 + 6\cdot 0 \\ 3\cdot 2 + 0\cdot 1 + 3\cdot 0 \\ 1\cdot 2 + 1\cdot 5 + 4\cdot 0 \end{array}\right] = \left[\begin{array}{c} 7 \\ 6 \\ 7 \\ \end{array}\right] \]
Kolonsal Kombinasyon Bakışı
Fakat matris çarpımına bakmanın bir yolu daha var, hatta bu bakış açısının daha önemli bile olduğu söylenebilir, o da \(A\)’nin kolonlarının kombine edilerek sağa sonuç olarak geçilmesi bakışıdır. Buna göre
\[ 2\cdot \left[\begin{array}{ccc} 1 \\ 3 \\ 1 \\ \end{array}\right] + 5\cdot \left[\begin{array}{c} 1 \\ 0 \\ 1 \\ \end{array}\right] + 0\cdot \left[\begin{array}{c} 6 \\ 3 \\ 4 \\ \end{array}\right] = \left[\begin{array}{c} 7 \\ 6 \\ 7 \\ \end{array}\right] \]
Tabii burada ikinci “matris” aslinda bir vektör, ama o vektör de matris olsaydı,
A = np.array([[1 ,1 , 6],[3 , 0 , 1],[1 , 1 , 4]])
x = np.array([[2], [5], [0]])
print ('vektor ile\n')
print (np.dot(A,x))
B = np.array([[2, 2, 2],[5, 5, 5],[0, 0, 0]])
print ('\nmatris ile\n')
print (np.dot(A,B))vektor ile
[[7]
[6]
[7]]
matris ile
[[7 7 7]
[6 6 6]
[7 7 7]]Satır Kombinasyon Bakışı
Sağdan çarpan vektörü bir genişleterek 2 boyutlu hale getirelim,
\[ \left[\begin{array}{ccc} 1 & 1 & 6 \\ 3 & 0 & 1 \\ 1 & 1 & 4 \\ \end{array}\right] \left[\begin{array}{ccc} 2 & 2 \\ 5 & 5 \\ 0 & 0 \\ \end{array}\right] \]
Satırsal bakışa göre soldaki matrisinin herhangi bir \(i\) satırındaki her öge, sağdaki matrisin tüm satırlarını kombine ederek sonucun \(i\) satırını ortaya çıkarır. Mesela en üst (birinci satır) için
\[ 1 \cdot \left[\begin{array}{cc} 2 & 2 \end{array}\right] + 1 \cdot \left[\begin{array}{cc} 5 & 5 \end{array}\right] + 6 \cdot \left[\begin{array}{cc} 0 & 0 \end{array}\right] = \left[\begin{array}{cc} 7 & 7 \\ \vdots & \vdots \\ \vdots & \vdots \end{array}\right] \]
Diğerleri için benzer işlem uygulanır,
\[ 3 \cdot \left[\begin{array}{cc} 2 & 2 \end{array}\right] + 0 \cdot \left[\begin{array}{cc} 5 & 5 \end{array}\right] + 1 \cdot \left[\begin{array}{cc} 0 & 0 \end{array}\right] = \left[\begin{array}{cc} 7 & 7 \\ 6 & 6 \\ \vdots & \vdots \end{array}\right] \]
ve böyle devam edilir.
Kolon Satır Çarpım Bakışı
Bir diğer bakış açısı \(A\)’nin bir kolonunu, çarpan matris \(B\)’nin bir satırı ile çarpılıp, bu her çarpımdan bir matris elde etmek, ve sonra bu matrisleri toplamaktır. Örnekte görelim,
\[ \left[\begin{array}{ccc} 1 & 1 & 6 \\ 3 & 0 & 1 \\ 1 & 1 & 4 \\ \end{array}\right] \left[\begin{array}{ccc} 2 & 2 \\ 3 & 1 \\ 9 & 5 \\ \end{array}\right] \]
Boyutları düşünürsek daha açık hale gelebilir, soldaki matrisin bir kolonu 3 x 1 boyutunda, sağdaki bir satır 1 x 2 boyutunda. Sonuç tabii ki 3 x 2 boyutunda bir matris olacaktır ve bu boyuttaki bir matris her kolon-satır çarpımından elde edilecektir. Bu durumda mesela ilk yapılan çarpım,
\[ \left[\begin{array}{ccc} 1 \\ 3 \\ 1 \\ \end{array}\right] \left[\begin{array}{ccc} 2 & 2 \end{array}\right] \]
çarpımı olur. Hesabı altta yapalım,
A = np.array([[1],[3],[1]])
b1 = np.array([[2, 2]])
print (np.dot(A,b1))[[2 2]
[6 6]
[2 2]]Bu şekilde diğer kolon-satır kombinasyonlarını da yaparsak (birinci kolon ile birinci satır, ikinci kolon ile ikinci satır, üçüncü kolon ile üçüncü satır çarpılacak),
A = np.array([[1 ,1 , 6],[3 , 0 , 1],[1 , 1 , 4]])
B = np.array([[2, 2],[3, 1],[9, 5]])
i = 0; r1 = np.dot(A[:,i].reshape(3,1),B[i,:].reshape(1,2))
i = 1; r2 = np.dot(A[:,i].reshape(3,1),B[i,:].reshape(1,2))
i = 2; r3 = np.dot(A[:,i].reshape(3,1),B[i,:].reshape(1,2))
print (r1)
print (r2)
print (r3)[[2 2]
[6 6]
[2 2]]
[[3 1]
[0 0]
[3 1]]
[[54 30]
[ 9 5]
[36 20]]print ('kolon-matris carpim toplami')
print (r1+r2+r3)
print ('tum carpim')
print (A.dot(B))kolon-matris carpim toplami
[[59 33]
[15 11]
[41 23]]
tum carpim
[[59 33]
[15 11]
[41 23]]Aynı sonuca varıldığını görüyoruz.
Vektörler
Bir vektör bir yön ve büyüklüktür, başlangıç noktası olarak genellikle orijin kabul edilir. 1,2, ya da daha fazla boyutta bir sayı listesi ile gösterilebilir, tek boyutta ise bu tabii ki bir skalar ile aynı şeydir [5].
Toplamak
İki boyutta bir örnek görelim, iki vektör \(a,b\) var, toplamları

Toplam sanki birinci vektörü alıp diğerinin bittiği yerden başlatmak gibi, varılan yeri gösteren yeni vektör toplam vektörüdür. Çıkartmak ise aynı yerden başlayan iki vektörde birinin sonundan diğerine sonuna giden vektörü bulmak gibidir. Aslında toplam üzerinden çıkartma doğrulabilir, \(a-b\) düşünürken \(-b\) diye yeni bir vektör yaratırız (yani vektörü tersine çeviririz) ve \(a+(-b)\) ile toplam işlemini yaparız.
Çıkartmak

Kosinüsler Kanunu (Law of Cosines)
Şöyle bir üçgen olduğunu düşünelim [7],
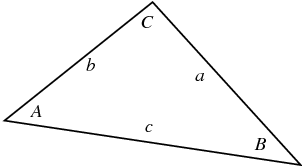
Eğer, mesela C’nin 90 derece olduğunu bilseydik, Pitagor kuralından
\[ c^2 = a^2 + b^2 \]
diyebilirdik. Ama \(C < 90\) ise, farklı bir formül kullanılabilir,
\[ c^2 = a^2 + b^2 - 2 a b \cos C \]
Eğer \(C=90\) ise \(\cos(90) = 0\) olduğu için Pitagor kuralını elde ettiğimizi görürüz.
Üstteki kurala Kosinüsler Kanunu denir, ispatı şöyle,
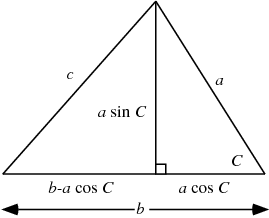
Üstteki üçgene bakarsak,
\[ c^2 = (a \sin C)^2 + (b-a\cos C)^2 \]
\[ = a^2 \sin^2 C + b^2 - 2 a b \cos C + a^2 \cos^2 C \]
\[ c^2 = a^2 + b^2 - 2 a b \cos C \]
Noktasal Çarpım
İki boyutta iki vektör \(\vec{a},\vec{b}\) olduğunu düşünelim. Bu vektör ögelerini \(\vec{a} = [a_1, a_2]\) ve \(\vec{b} = [b_1, b_2]\) diye gösterirsek, noktasal çarpım \(\vec{a} \cdot \vec{b}\) her iki vektörün tekabül eden öğelerinin çarpımının toplamıdır, yani
\[ \vec{a} \cdot \vec{b} = a_1 b_1 + a_2 b_2 \]
Daha yüksek boyutlarda benzer işlem devam ettirilir.
Norm
Bir vektörün uzunluğunun, büyüklüğünün, ya da normu, ki \(||\vec{a}||\) ile gösterilebilir, karesi
\[ ||\vec{a}||^2 = \vec{a} \cdot \vec{a} \]
Bu kurallara uygun çünkü
\[ (\vec{a} \cdot \vec{a})^2 = a_1 a_1 + a_2 a_2 \]
Ya da
\[ ||\vec{a}|| = \sqrt{\vec{a} \cdot \vec{a}} = \sqrt{a_1 a_1 + a_2 a_2} \]
Aslında büyüklük formülü Pitagor üçgen formülünden hareketle de anlaşılır çünkü herhangi bir vektör düşünürsek, \(a_1,a_2\) ya da \(x\) ekseninde \(a_1\) \(y\) ekseninde \(a_2\) olan bir nokta düşünürsek bu noktaya olan orijinden olan uzaklık (vektör) Pitagor formülü ile hesaplanabilirdi, \(\sqrt{a_1^2 + a_2^2}\).
Noktasal çarpım şu şekilde de hesaplanabilir,
\[ \vec{a} \cdot \vec{b} = ||\vec{a}|| ||\vec{b}|| \cos\theta \]
İspat
Alttaki şekle bakarsak,
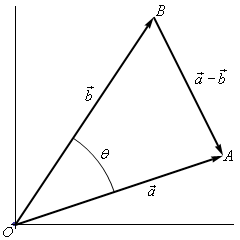
Bu üçgenin kenarları arasında Kosinüsler Kanunu uygularsak,
\[ ||\vec{a}-\vec{b}||^2 = ||\vec{a}||^2 + ||\vec{b}||^2 - 2 ||\vec{a}|| ||\vec{b}|| \cos\theta \qquad (1) \]
Norm açılımından hareketle
\[ ||\vec{a}-\vec{b}||^2 = (\vec{a}-\vec{b}) \cdot (\vec{a}-\vec{b}) \]
Noktasal çarpımı parantezler üzerinden açarsak,
\[ = \vec{a}\cdot\vec{a} - \vec{a}\cdot\vec{b} - \vec{b}\cdot\vec{a} + \vec{b}\cdot\vec{b} \]
\[ = ||\vec{a}||^2 - 2\vec{a}\cdot\vec{b} + ||\vec{b}||^2 \]
\[ ||\vec{a}||^2 - 2\vec{a}\cdot\vec{b} + ||\vec{b}||^2 = ||\vec{a}||^2 + ||\vec{b}||^2 - 2 ||\vec{a}|| ||\vec{b}|| \cos\theta \]
\[ - 2\vec{a}\cdot\vec{b} = - 2 ||\vec{a}|| ||\vec{b}|| \cos\theta \]
\[ \vec{a}\cdot\vec{b} = ||\vec{a}|| ||\vec{b}|| \cos\theta \]
Üstteki eşitlik veri analizinde kullanışlı bulunmuştur, mesela kimisi müşterileri \(D\) boyutunda vektörler olarak temsil edebilir, 1. öğe yaş, 2. öğe boy, vs. gibi bilgiler olabilir ve iki vektörün birbirine ne kadar “yakın’’ olduğu iki vektörün arasındaki açısal uzaklık üzerinden ölçülebilir,
\[ \cos\theta = \frac{\vec{a}\vec{b}}{||\vec{a}|| ||\vec{b}||} \]
Eğer vektörler baştan normalize edilmiş ise bölme işlemine de gerek kalmaz, tek bir noktasal çarpım ile kabaca bir benzerlik ölçütü elde edilmiş olur.
Bir diğer kullanım alanı fizikte “yapılan iş’’ hesabı. İş, uygulanan kuvvet çarpı mesafeden elde edilir fakat mesela bir kuvvet alanı \(\vec{F}\) her yerde farklı olabilir ayrıca bu alanda belli bir \(\vec{d}\) yolunda hareket eden bir parçacığı düşünürsek, parçacık bazen kuvvete karşı bazen onunla beraber hareket ediyor olabilir, bunun ne oranda olduğunun hesabı \(\vec{F}\)’yi \(\vec{d}\) üzerine skalar olarak yansıtmakla hesaplanır [3], \(W = \vec{F} \cdot \vec{d}\).
Diklik
İki vektörün birbirine dik olup olmadığı (orthogonality) testi de noktasal çarpım ile yapılır. \(\cos(90) = 0\) olduğuna göre \(\vec{a}\cdot\vec{b}\) çarpımı sıfır ise iki vektör dik demektir.
Kaynaklar
[5] Math Insight, https://mathinsight.org/vector_introduction