ki $\mu$ bizim seçeceğimiz bir parametre olabilir. Çözüm için mesela Newton metodunu kullanabiliriz, fakat tek bir problem var, Newton ve ona benzer diğer optimizasyon metotları için türev almak gerekli, fakat $\phi_{tv}$'deki L1-norm'unun (tek boyutta mutlak değer fonksiyonu) $x=0$'da türevi yoktur (birinci terimdeki Oklit normunun karesi alındığı için onun iki kere türevi alınabilir). Bu durumda $\phi_{tv}$'yi yaklaşık olarak temsil edebilirsek, onun da türevi alınır hale gelmesi sağlayabiliriz. Bu yeni fonksiyona $\phi_{atv}$ diyelim,

$$ \phi_{atv} = \sum_{i=1}^{n-1} \left( \sqrt{ \epsilon^2 + (x_{i+1})-x_i } - \epsilon \right) $$

ki $\epsilon > 0$ yaklaşıklamanın seviyesini ayarlıyor. Bu fonksiyonun iyi bir yaklaşıklama olduğunu görmek zor değil, toplam içindeki kısmı deneyerek görelim,

import numpy as np

eps = 1e-6
mu = 50.0

def norm_tv(x):
   return np.sum(np.abs(np.diff(x)))

def norm_atv(x):
   return np.sum(np.sqrt(eps + np.power(np.diff(x),2)) - eps)

xcor = np.random.randn(1000)

print (norm_tv(xcor))
print (norm_atv(xcor))

1103.2561038302395
1103.2571969067808

Üstteki fonksiyonun iki kez türevi alınabilir. Şimdi analitik şekilde devam etmeden önce pür sayısal açıdan bir çözüme bakalım. Üstteki fonksiyonları direk kodlayarak ve sayısal türev üzerinden işleyebilen bir kütüphane çağrısıyla hedefi minimize edelim, eldeki sinyal,

import pandas as pd
df = pd.read_csv('xcor.csv',header=None)
xcor = np.reshape(np.array(df[0]), (5000,1))
plt.plot(range(len(xcor)), xcor)
plt.savefig('func_60_tvd_01.png')

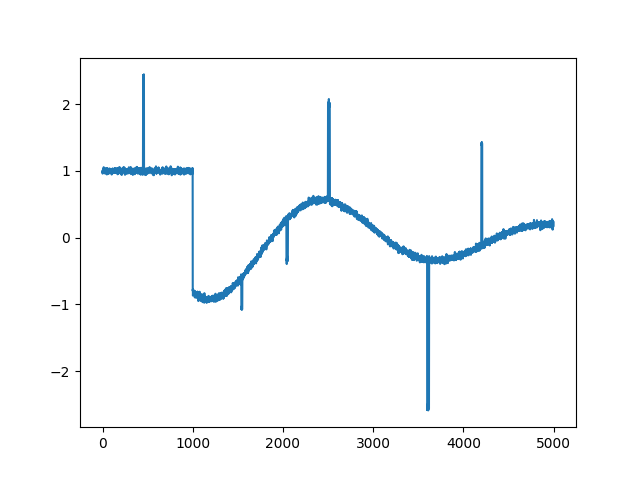
Kütüphane çağrısı ile

x0 = np.zeros(len(xcor))

from scipy.optimize import minimize, Bounds, SR1, BFGS

def phi(x):
   return np.sum(np.power(x-xcor, 2)) + mu*norm_atv(x)

opts = {'maxiter': 400, 'verbose': 2}

res = minimize (fun=phi,
                x0=x0,
                options=opts,
                jac='2-point',
                hess=BFGS(),
                method='trust-constr'
                )

plt.plot(range(5000), res.x)
plt.savefig('func_60_tvd_02.png')

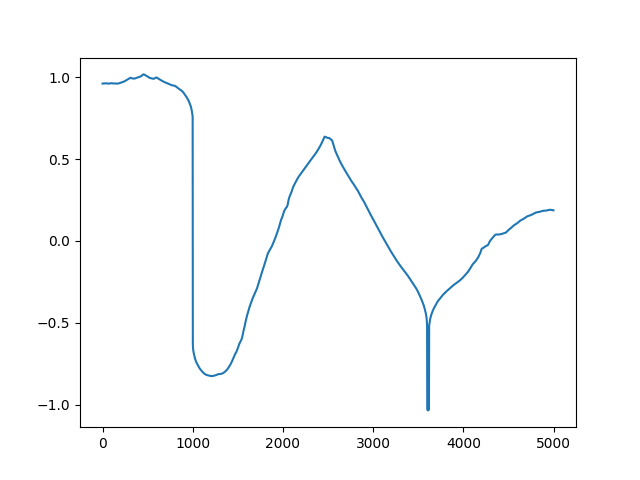
Sonuç fena olmadı. Fakat üstteki yaklaşımın hesabı uzun sürecektir, eğer eldeki problem hakkında bazı ek şeyler biliyorsak, bu bilgileri dahil ederek elde edilen çözüm daha hızlı olabilir. Mesela analitik olarak türevler Jacobian ve Hessian bulunabilir, Newton adımı elle kodlanabilir, ayrıca problemdeki matrislerde muhtemel bir seyreklikten (sparsity) faydalanılabilir.

Hedef fonksiyonu, $\psi(x)$ diyelim, için birinci ve ikinci türev,

$$ \nabla \psi(x) = 2 (x-x_{cor}) + \mu \nabla \phi_{atv}(x), \qquad \nabla^2 \psi(x) = 2 I + \mu \nabla^2 \phi_{atv} (x) $$

Zincirleme Kuralı uygulandı tabii, ve şimdi $\phi_{atv}$ üzerindeki türevleri bulmak gerekiyor. Sorun değil, daha önceki yaklaşıklamayı bunun için yapmıştık zaten. Yaklaşık fonksiyonu genel olarak belirtirsek,

$$ f(u) = \sqrt{\epsilon^2 + u^2} - \epsilon $$

Bu fonksiyonun 1. ve 2. türevi

$$ f'(u) = u(\epsilon^2 + u^{-1/2} ), \qquad f"(u) = \epsilon^2 (\epsilon^2 + u^2)^{-3/2} $$

Şimdi bir $F$ tanımlayalım,

$$ F(u_1,..., u_{n-1}) = \sum_{i=1}^{n-1} f(u_i) $$

Yani $F(u)$ $u$'nun bileşenlerinin yaklaşık L1 norm'unun toplamıdır. Nihai amacımız bu tanımdan bir $\phi_{atv}$ ifadesine ulaşmak. $F$'in gradyanı ve Hessian'ı

$$ \nabla F(u) = \left[\begin{array}{ccc} f'(u_1) & \dots & f'(u_{n-1}) \end{array}\right] $$

$$ \nabla^2 F(u) = \mathrm{diag} \left[\begin{array}{ccc} f"(u_1) & \dots & f"(u_{n-1}) \end{array}\right] $$

Eğer bir ileri farklılık matrisi $D$ tanımlarsak,

$$ D = \left[\begin{array}{ccccc} -1 & 1 & & & \\ & -1 & 1 & & \\ & & \ddots & \ddots & \\ & & & -1 & 1 \end{array}\right] $$

O zaman $\phi_{atv}(x) = F(Dx)$ diyebiliriz. Bir $x$ vektörünü üstteki matris ile soldan çarpınca öğeleri $\left[\begin{array}{ccc} x_2-x_1 & x_3-x_2 & \dots \end{array}\right]$ şeklinde giden bir yeni vektör elde edeceğimizi doğrulamak zor değil. Yine Zincirleme Kuralını uygularsak,

$$ \nabla \phi_{atv}(x) = D^T \nabla F(Dx), \qquad \nabla^2 \phi_{atv}(x) = D^T \nabla^2 F(Dx) D $$

Hepsini bir araya koyarsak

$$ \nabla \psi(x) = 2(x-x_{cor}) + \mu D^T \nabla F(Dx) $$

$$ \nabla^2 \psi(x) = 2 I + \mu D^T \nabla^2 F(Dx) D $$

Kodlamayı alttaki gibi yapabiliriz,

import pandas as pd
import scipy.sparse as sps
import scipy.sparse.linalg as slin

MU = 50.0
EPSILON = 0.001

ALPHA = 0.01;
BETA = 0.5;
MAXITERS = 100;
NTTOL = 1e-10;

n = len(xcor)
data = np.array([-1*np.ones(n), np.ones(n)])
diags = np.array([0, 1])
D = sps.spdiags(data, diags, n-1, n)

x = np.zeros((len(xcor),1))

for iter in range(MAXITERS):
   d = D.dot(x)
   val1 = np.dot((x-xcor).T,(x-xcor))
   val2 = np.sqrt(EPSILON**2 + np.power(d,2))
   val3 = EPSILON*np.ones((n-1,1))
   val = np.float(val1 + MU*np.sum(val2 - val3))
   grad1 = 2*(x-xcor)
   grad2 = MU*D.T.dot(d / np.sqrt(EPSILON**2 + d**2))
   grad = grad1 + grad2
   hess1 = 2*sps.eye(n)
   hess2 = EPSILON**2*(EPSILON**2+d**2)**(-3/2)
   hess2 = hess2.reshape((n-1))
   hess3 = sps.spdiags(hess2, 0, n-1, n-1)

   hess = hess1 + MU*hess3.dot(D).T.dot(D)
   v = slin.spsolve(-hess, grad)
   v = np.reshape(v, (n,1))
   lambdasqr = np.float(np.dot(-grad.T,v))
   if lambdasqr/2 < NTTOL: break
   t = 1;
   while True:
      tmp1 = np.float(np.dot((x+t*v-xcor).T,(x+t*v-xcor)))
      tmp2 = MU*np.sum(np.sqrt(EPSILON**2+(D*(x+t*v))**2)-EPSILON*np.ones((n-1,1)))
      tmp3 = val - ALPHA*t*lambdasqr
      if tmp1 + tmp2 < tmp3: break
      t = BETA*t

   x = x+t*v

plt.plot(range(n),xcor)
plt.plot(range(n),x,'r')
plt.savefig('func_60_tvd_03.png')

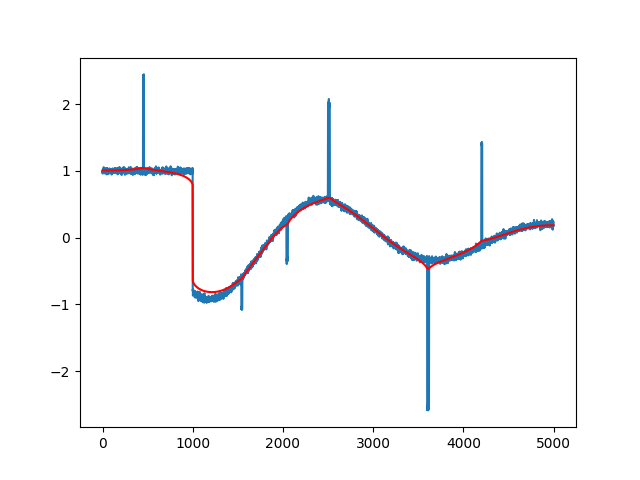
Çok daha iyi bir gürültüsüz sonuç elde ettik, üstteki bu işlem çok daha hızlı.

Görüntüden Gürültü Silmek

Aynen tek boyutlu sinyalden gürültü silebildiğimiz gibi iki boyutlu görüntüden de gürültü silmek mümkün. Bu durumda tam varyasyon

$$ \sum_{i=2}^{m} \sum_{j=2}^{n} (|U_{i,j} - U_{i-1,j}| + |U_{i,j} - U_{i,j-1}|) $$

olabilir, yani her pikselin bir yanindaki ve bir altındaki pikselle olan uzaklığının L1-norm'unu almak. Üstteki hesabı yapmak için aslında yine daha önce hesapladığımız $D$ matrisini kullanabiliriz. Bir $X$ imajı üzerinde $DX$ hesabı, yani $D$ ile soldan çarpım dikey farklılıkları, sağdan çarpım $XD$ ise yatay farklılıkları verecektir.

import scipy.sparse as sps

X = [[1, 2, 3, 4],
     [5, 6, 7, 8],
     [1, 2, 3, 4],
     [5, 6, 7, 8]]

X = np.array(X)
print (X)
n = X.shape[0]
data = np.array([-1*np.ones(n), np.ones(n)])
diags = np.array([0, 1])
D = sps.lil_matrix(sps.spdiags(data, diags, n, n))
print (D.todense())
print ('Dikey Farklilik')
print (D.dot(X))
print ('Yatay Farklilik')
print (D.transpose().dot(X.T))

[[1 2 3 4]
 [5 6 7 8]
 [1 2 3 4]
 [5 6 7 8]]
[[-1.  1.  0.  0.]
 [ 0. -1.  1.  0.]
 [ 0.  0. -1.  1.]
 [ 0.  0.  0. -1.]]
Dikey Farklilik
[[ 4.  4.  4.  4.]
 [-4. -4. -4. -4.]
 [ 4.  4.  4.  4.]
 [-5. -6. -7. -8.]]
Yatay Farklilik
[[-1. -5. -1. -5.]
 [-1. -1. -1. -1.]
 [-1. -1. -1. -1.]
 [-1. -1. -1. -1.]]

L1 norm yaklaşıksallığı için daha önceki yöntemi kullanabiliriz.

Gradyan almak için ise bu sefer tensorflow paketini kullanacağız [5]. Bir vektöre göre değil bir matrise göre türev alıyoruz, bunu sembolik yapmak yerine sembolik yaklaşım kadar kuvvetli olan otomatik türev ile gradyanı elde edebiliriz.

Üstteki tüm hesapları TF ile bir hesap grafiği içinde kodlayıp, tf.gradients ile hedef fonksiyonunun gradyanını alacağız, ve standart gradyan inişi optimizasyonu ile bir noktadan başlayıp gradyan yönü tersinde adım atarak minimum noktaya varmaya uğraşacağız.

from skimage import io
import tensorflow as tf

MU = 50.0
EPSILON = 0.001
n = 225

img = io.imread('lena.jpg', as_gray=True)
io.imsave('lenad0.jpg', img)
img = io.imread('lena-noise.jpg', as_gray=True)
io.imsave('lenad1.jpg', img)
xorig = tf.cast(tf.constant( io.imread('lena-noise.jpg', as_gray=True)),dtype=tf.float32)
x = tf.placeholder(dtype="float",shape=[n,n],name="x")

D = np.zeros((n,n))
idx1, idx2 = [], []
for i in range(n):
    idx1.append([i,i])
    if i<n-1: idx2.append([i,i+1])
idx = idx1 + idx2
ones = [1.0 for i in range(n)]
ones[n-1] = 0
negs = [-1.0 for i in range(n-1)]
negs[n-2] = 0
vals = ones + negs
vals = np.array(vals).astype(np.float32)
D = tf.SparseTensor(indices=idx, values=vals, dense_shape=[n, n])


diff = tf.square(tf.norm(xorig-x, ord='euclidean'))

Ux = tf.sparse_tensor_dense_matmul(D, x)
Uy = tf.sparse_tensor_dense_matmul(tf.sparse_transpose(D), tf.transpose(x))
Uy = tf.transpose(Uy)

fUx = tf.reduce_sum(tf.sqrt(EPSILON**2 + tf.square(Ux)) - EPSILON)
fUy = tf.reduce_sum(tf.sqrt(EPSILON**2 + tf.square(Uy)) - EPSILON)

phi_atv = fUx + fUy

psi = diff + MU*phi_atv
g = tf.gradients(psi, x)
g = tf.reshape(g,[n*n])

init = tf.global_variables_initializer()

sess = tf.Session()

sess.run(init)

def tv(xvec):
    xmat = xvec.reshape(n,n)
    p = sess.run(psi, {x: xmat} )
    return p

def tv_grad(xvec):
    xmat = xvec.reshape(n,n)
    gres = sess.run(g, {x: xmat} )
    return gres

x0 = np.zeros(n*n)
xcurr = x0

N = 130
for i in range(1,N):
    gcurr = tv_grad(xcurr)
    gcurr /= gcurr.max()/0.3
    chg = np.sum(np.abs(xcurr))
    xcurr = xcurr - gcurr

xcurr /= xcurr.max()/255.0
io.imsave('lenad2.jpg', np.reshape(xcurr,(n,n)))

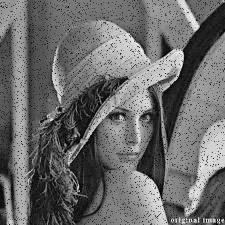
Yine total varyasyon kullanan ama farklı optimizasyon çözücüyle hesabı yapan bir yöntem tlv_prim_dual.py kodunda [1], sonuç (soldaki)

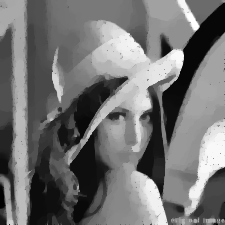
Ayrıca cvxpy adlı bir paket üzerinden aynı şeyi kodlayabiliriz, yani

$$ \min_{\beta \in \mathbb{R}^n} \frac{1}{2} \sum_{i=1}^{n} (y_i - \beta_i)^2 + \lambda \sum_{(i,j) \in E)} |\beta_i - \beta_j| $$

import cvxpy

lam = 35.0

u_corr = plt.imread("lenad1.jpg")

rows, cols = u_corr.shape

U = cvxpy.Variable(shape=(rows, cols))

obj = cvxpy.Minimize(0.5 * cvxpy.sum_squares(u_corr-U) + lam*cvxpy.tv(U))

prob = cvxpy.Problem(obj)

prob.solve(verbose=True, solver=cvxpy.SCS)

plt.imshow(U.value, cmap='gray')
plt.imsave(lena4.jpg', U.value, cmap='gray')

Üstteki sağdaki resim bu sonucu gösteriyor. Bu yaklaşımda cvxpy.tv ile tam varyasyon hesabını yapan kütüphanenin kendi iç çağrısını kullandık.

Kaynaklar

[1] Mordvintsev, ROF and TV-L1 denoising with Primal-Dual algorithm, https://github.com/znah/notebooks/blob/master/TV_denoise.ipynb

[2] Chambolle, An introduction to continuous optimization for imaging, https://hal.archives-ouvertes.fr/hal-01346507/document

[3] Afonso, Fast Image Recovery Using Variable Splitting and Constrained Optimization, http://www.lx.it.pt/~mtf/Afonso_BioucasDias_Figueiredo_twocolumn_v7.pdf

[4] Boyd, Additional Exercises for Convex Optimization https://web.stanford.edu/~boyd/cvxbook/bv_cvxbook_extra_exercises.pdf

[5] Bayramlı, Bilgisayar Bilim, Yapay Zeka, Tensorflow