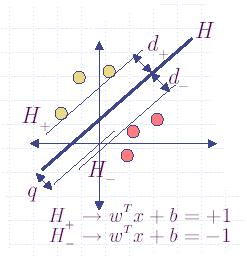
En basit halleriyle SVM’ler risk minimize eden lineer sınıflayıcısıdırlar.
\[ R(\Theta) \leq J(\Theta) = R_{emp}(\Theta) + \sqrt{ \frac{h \times (\log(\frac{2N}{h}) + 1) - \log(\frac{\eta}{4})}{N}} \]
h: sınıflayıcının kapasitesi
N: eğitim verisinde kaç veri noktası olduğu
Vapnik ve Chernovenkis \(1-\eta\) olasılıkla ispaladı ki üstteki denklem doğrudur. SVM algoritması hem \(h\) değerini hem de sayısal, ölçümsel riski aynı anda minimize etmektedir, ve bunu sınır noktalarını noktalarını ayırmakla yapmaktadır. Türetelim,

Karar düzlemi: \(w^{T}x + b=0\)
Şöyle bir tanım yapalım:
\[ q = \min_{x}\big\|x - 0\big\|, \quad w^T x+b=0 \textrm { sartina gore } \]
\(q\), \(H^{+}\) ve \(H^{-}\) formüllerini ileride kullanacağız.
Lagrange:
\[ \min_{x}\frac{1}{2} \big\|x - 0\big\|^2+\lambda(w^{T}x+b) \]
Gradyanı alalım ve 0 değerine eşitleyelim,
\[ \frac{\partial}{\partial x} ( \frac{1}{2} x^T x + \lambda( w^T x + b ) ) = 0 \]
\[ x + \lambda w = 0 \]
\[ x = -\lambda w \]
Üsteki sonucu \(w^T x+b=0\) şartına sokalım,
\[ w^T(-\lambda w) + b = 0 \]
\[ \lambda = \frac{b}{w^Tw} \]
Yani çözüm
\[ \hat{x} = - \bigg( \frac{b}{w^Tw} \bigg) w \]
O zaman \(q\)
\[ q = || \hat{x}-0 || = \bigg|\bigg| - \frac{b}{w^Tw} w \bigg|\bigg| \]
\[ \big|\frac{b}{w^Tw}\big| \times \sqrt{w^Tw} \]
\[ q = \frac{|b|}{||w||} \]
Tanım:
\[ H^{+} = w^{T}x + b=+1 \]
\[ H^{-} = w^{T}x + b=-1 \]
grafikte görüldüğü gibi yani. Üstteki şekilde tanımın bir zararı yok (çünkü +1,-1 sabit durunca ayraç genişlemesi nasıl olacak diye düşünülebilir, ama bu tanım genelliği kaybetmeden yapabilabiliyor çünkü \(b,w\) değerlerinde hala oynanabilir.
\(q^{+}\) ve \(q^{-}\) değerlerini hesapla
\[ q^{+} = \frac{|b-1|}{||w||} \]
\[ q^{-} = \frac{|-b-1|}{||w||} \]
Ayraç o zaman şöyle
\[ m=q^{+}+q^{-} = \frac{|b-1-b-1|}{||w||} = \frac{|-2|}{||w||} = \frac{2}{||w||} \]
Ayraçların olabildiğince ayırmasını istiyorsak \(m\)’i arttırız (yani \(\frac{2}{||w||}\)’i maksimize ederiz), ya da \(||w||\) değerini minimize ederiz.
Sınırlar
Veri noktalarını öyle sınıflamak istiyoruz ki + ve - noktalar hiperdüzlemlerin doğru noktalarında kalsınlar.
\[ w^{T}x+b \geq +1, \quad \forall y_{i}=+1 \]
\[ w^{T}x+b \leq -1, \quad \forall y_{i}=-1 \]
Bu iki denklemi birleştirelim
\[ y_{i}(w^{T}x+b)-1 \geq 0 \]
Her şeyi biraraya koyalım
\[ \min_w \frac{1}{2}{||w||^2}, \quad y_{i}(w^Tx_{i}+b)-1 \ge 0 \textrm{ olsun. }\]
Bu form tanıdık geliyor mu? Bu qp ile çözülebilecek karesel (quadratic) bir formül, programdır!
qp
Python dilinde cvxopt paketi vardır Matlab Optimization Toolbox’da qp() var. QP fonksiyonları problemleri genelde
\[\frac{1}{2}x^{T}Px+q^{T}x\]
formunda görmek isterler. Biraz önce elde ettiğimiz denklemi bu istenen formata doğru “masajlayabiliriz’’
İkiz (dual)
SVM ihtiyaçları için ikiz formül (dual) ile çalışmak daha rahattır Lagrange (tekrar) oluşturalım, türevi alalım, ve sıfıra eşitleyelim. Bunun sonucunda elimize KKT noktaları geçecektir
\[ L_{p} = \frac{1}{2}||w||^{2}-\sum_{i}\alpha_{i}(y_{i}(w^{T}x_{i}+b)-1) \]
\[ \frac{\partial}{\partial w} L_{p} = w-\sum_{i}\alpha_{i}y_{i}x_{i}=0 \]
\[ w = \sum_{i}\alpha_{i}y_{i}x_{i} \]
\[ \frac{\partial}{\partial b} L_{p} = -\sum_{i}\alpha_{i}y_{i}=0 \]
Üstteki iki denklemi asal (primal) denkleme koyduğumuz zaman
\[ \textrm{ Maksimize et } L_{D}= \sum_{i}\alpha_{i}-\frac{1}{2} \sum_{i} \sum_{j} \alpha_{i} \alpha_{j} y_{i}y_{j}x_{i}^{T}x_{j} \]
sınırlar
\[ \sum_{i}\alpha_{i}y_{i}=0 \]
\[ \alpha_{i} \geq 0 \]
qp
Bu yine qp() formunda bir problem! Sadece bu sefer çözeceğimiz değişkenler \(\alpha_i\)’lar, \(x\)’lar değil. Üstteki denklem şu forma \(\frac{1}{2}x^{T}Px+q^{T}x\) masajlanabilir Bunun yapmak için \(P_{i,j}\)’ye \(-y_{i}y_{j}x_{i}^{T}x_{j}\) değerini atarız. Ve qp’yi çağırırız Sonuç bir \(\alpha\)’lar listesi olacaktır.
\(b\) değerini hesaplamak
KKT koşulunun sebebiyle sıfır olmayan her \(\alpha_{i}\) için ana problemde ona tekabül eden kısıtlayıcı şart şıkıdır (tight), yani bir eşitliktir. O zaman sıfır olmayan her \(\alpha_{i}\) için \(b\)’yi \(w^{T}x_{i}+b = y_{i}\) ifadesini kullanarak hesaplarız. Sıfır olmayan her \(\alpha_{i}\)’dan gelen \(b\) yaklaşık olarak diğer other \(b\)’lere eşit olacaktır. Final \(b\)’yi hesaplamak için tüm \(b\)’lerin ortalamasını almak sayısal (numeric) olarak daha garantidir.
Sınıflayıcı Tamamlandı
Her yeni \(x\) noktası için artık \(sign(x^{T}w+b)\) ibaresini sınıflayıcımız olarak kullanabiliriz. \(-1\) ya da \(+1\) olarak geri gelecek sonuç bize yeni noktanın hangi sınıfa ait olduğunu söyleyecektir.
Örnek Çıktı
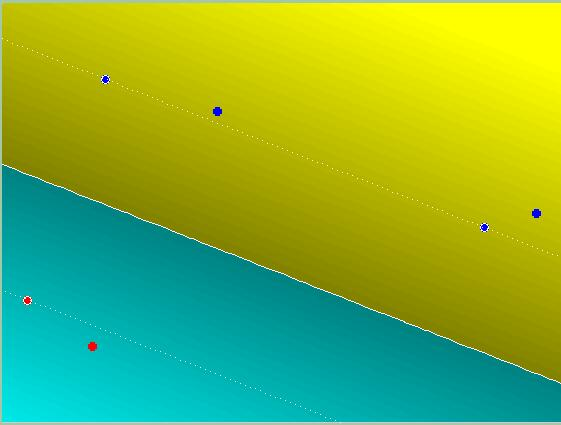
Çekirdekler (Kernels)
Şimdiye kadar lineer ayraçlardan bahsettik. SVM’ler lineer olmayan ayraçlarla da çalışabilir. Çok basit: Bir temel fonksiyon kullanarak girdiyi daha yüksek boyuta doğru bir önişlemden geçirirsek bunu başarabiliriz. Algoritmanın geri kalanı değişmeden kalacaktır.
Gayri Lineer Çekirdek
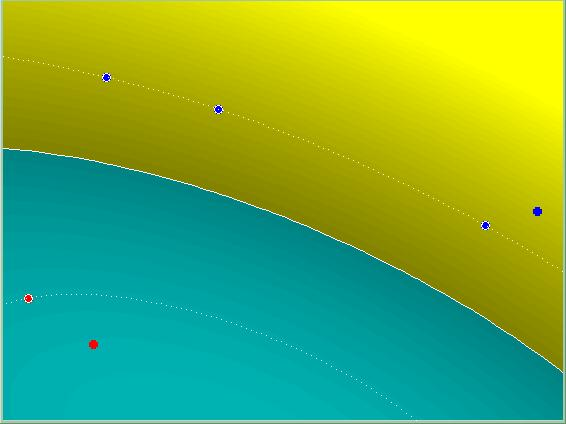
Esneme Payı Bazen bir problem ayrılmaya müsait olmayabilir. Çok üç noktalardaki bazı noktalar sınıflayıcının çalışmasını imkansız hale getirebilir Bunun çözümü için sınıflayıcıya “esneme payı” dahil edebiliriz. Mesela \(y_{i}=+1\) için verinin yanlış tarafa düşmesini şu durumda izin verebiliriz: \(w^{T}+b \geq -0.03\) Fakat eklemek gerekir ki bu tür noktaların “çok fazla’’ olmasını da istemiyoruz, bu sebeple bu”yanlış” noktaların sayısına da bir ceza getirebiliriz.
from numpy import linalg
import cvxopt
import cvxopt.solvers
def svm(X, y):
n_samples, n_features = X.shape
# Gram matrix
K = np.zeros((n_samples, n_samples))
for i in range(n_samples):
for j in range(n_samples):
K[i,j] = np.dot(X[i], X[j])
P = cvxopt.matrix(np.outer(y,y) * K)
q = cvxopt.matrix(np.ones(n_samples) * -1)
A = cvxopt.matrix(y, (1,n_samples))
b = cvxopt.matrix(0.0)
G = cvxopt.matrix(np.diag(np.ones(n_samples) * -1))
h = cvxopt.matrix(np.zeros(n_samples))
# solve QP problem
solution = cvxopt.solvers.qp(P, q, G, h, A, b)
print (solution)
# Lagrange multipliers
a = np.ravel(solution['x'])
print ("a", a)
# Support vectors have non zero lagrange multipliers
ssv = a > 1e-5
ind = np.arange(len(a))[ssv]
a = a[ssv]
sv = X[ssv]
sv_y = y[ssv]
print ("%d support vectors out of %d points" % (len(a), n_samples))
print ("sv", sv)
print ("sv_y", sv_y)
# Intercept
b = 0
for n in range(len(a)):
b += sv_y[n]
b -= np.sum(a * sv_y * K[ind[n],ssv])
b /= len(a)
# Weight vector
w = np.zeros(n_features)
for n in range(len(a)):
w += a[n] * sv_y[n] * sv[n]
print ("a", a)
return w, b, sv_y, sv, a
X = np.array([[3.,3.],[4.,4.],[7.,7.],[8.,8.]])
y = np.array([1.,1.,-1.,-1.])
w, b, sv_y, sv, a = svm(X, y)
print ("w", w)
print ("b", b)
print ('test points')
print (np.dot([2.,2.], w) + b) # > 1
print (np.dot([9.,9.], w) + b) # < -1 pcost dcost gap pres dres
0: -2.9061e-01 -5.0286e-01 6e+00 2e+00 1e+00
1: -3.6857e-02 -3.0976e-01 3e-01 3e-16 2e-15
2: -1.0255e-01 -1.2816e-01 3e-02 3e-17 1e-15
3: -1.1074e-01 -1.1128e-01 5e-04 2e-17 9e-16
4: -1.1111e-01 -1.1111e-01 5e-06 3e-17 3e-16
5: -1.1111e-01 -1.1111e-01 5e-08 4e-17 4e-16
Optimal solution found.
{'x': <4x1 matrix, tc='d'>, 'y': <1x1 matrix, tc='d'>, 's': <4x1 matrix, tc='d'>, 'z': <4x1 matrix, tc='d'>, 'status': 'optimal', 'gap': 5.330207369919097e-08, 'relative gap': 4.797188223915408e-07, 'primal objective': -0.11111107426109383, 'dual objective': -0.11111112756316754, 'primal infeasibility': 4.388541835878497e-17, 'dual infeasibility': 3.646862906299076e-16, 'primal slack': 2.76375125177696e-08, 'dual slack': 7.403425105865937e-08, 'iterations': 5}
a [2.76375125e-08 1.11111073e-01 1.11111073e-01 2.76375125e-08]
2 support vectors out of 4 points
sv [[4. 4.]
[7. 7.]]
sv_y [ 1. -1.]
a [0.11111107 0.11111107]
w [-0.33333322 -0.33333322]
b 3.666665418062399
test points
2.3333325387669808
-2.3333325387669817Not: İkizdeki \(L_d\)’yi maksimize
ediyoruz, fakat hala qp()’deki minimize ediciyi
çağırıyoruz. Bu sebeple tüm \(\alpha\)’ların toplamını temsil eden \(q\)’ların negatifini alıyoruz,
np.ones(n_samples) *-1 işleminde görüldüğü gibi. Formüldeki
karesel kısım içinde zaten \(-\frac{1}{2}\) negatif ibaresi var, böylece
geri kalan formülün değişmesine gerek yok.
Dayanaklı Kayıp Fonksiyonu ile SVM, Pegasos
SVM problemi alttaki fonksiyonu çözmek anlamına geliyordu,
\[ \min_w \frac{1}{2}{||w||^2}, \textrm{ s.t. } \quad y_{i}(w^Tx_{i}+b)-1 \ge 0 \]
ki bu bir karesel program idi ve cvxopt paketindeki
qp ile çözülebiliyordu. Bazıları \(b\) terimini de atıyorlar, ve
\[ \min_w \frac{1}{2}{||w||^2} + \sum \max \{ 0, 1-y_i (w^T x_i) \} \]
olarak yazıyorlar. Ayrıca regülarizasyonu kontrol etmek için bir \(\lambda\) sabiti de ekleniyor, yani üstte \(\lambda ||w||^2 / 2\) kullanılması lazım. Regülarize işlemi \(w\)’nin norm’unun küçük olmasını tercih eder, ki bu bazı \(w\) değerlerinin sıfıra gitmesini zorlar, yani bir tür özellik seçme işi bu şekilde gerçekleşmiş olur. Toplam işleminin içindeki fonksiyona “kayıp fonksiyonu (loss function)’’ ismi de verilir, eğer bu kayıp fonksiyonu tam üstteki gibi ise ona dayanaklı kayıp (hinge loss) denir. Üstte görülen \(\max\) ifadesi suna eşittir,
\[ Loss(w,x_i,y_i) = \left\{ \begin{array}{ll} 1-y_i \cdot (w \cdot x_i) & \textrm{ eğer } y_i \cdot (w \cdot x_i) < 1 \\ 0 & \textrm { diğer } \end{array} \right. \]
Eğer kayıp fonksiyonunun gradyanını alırsak,
\[ \nabla L = \frac{\partial Loss(w,x_i,y_i)}{\partial w} = \left\{ \begin{array}{ll} -y_i x_i & \textrm{ eğer } y_i \cdot (w \cdot x_i) < 1 \\ 0 & \textrm { diğer } \end{array} \right. \]
Böylece bir rasgele gradyan iniş (stochastic gradient descent) yaklaşımını kodlayabiliriz.
\[ w_{t+1} = w_t - \eta (\lambda w_t + \nabla L )\]
ki \(\eta\) gradyanın ne kadar güncellenme yapacağını kontrol eden bir sabittir.
Ufak Toptan Parçalar (Minibatching)
Güncelleme işlemi tüm veri üzerinde, her veri noktası için yapılabilir, ya da gradyan güncellemeleri toparlanarak belli sayıda adım sonrası bir toplam güncelleme yapılır. \(b\) büyüklüğündeki ufak parça \(B_t\) de rasgele seçilir, ve \(w\)’ye uygulanır [3].
\[ w_{t+1} = w_t - \eta \bigg( \lambda w_t + \frac{1}{b} \sum_{x_i,y_i \in B_t} \nabla L \bigg) \]
import numpy as np, pandas as pd
def predict(w, x):
return np.dot(w.reshape((len(x),1)).T,x)
def train_sgd(data, labels, lam, iter, batch_size):
m,n = data.shape; w = np.zeros(n)
idx = list(range(m)) # Convert range object to a list
eta = 0.0001
for t in range(1, iter):
w_delta = np.zeros(n)
np.random.shuffle(idx)
for j in range(batch_size):
i = idx[j]
p = predict(w, data[i,:])
if labels[i]*p < 1.:
w_delta += labels[i]*data[i,:]
w = (1.0 - eta*lam)*w + (eta/batch_size)*w_delta
return wimport numpy as np, pandas as pd, zipfile
with zipfile.ZipFile('svmdata.zip', 'r') as z:
df = pd.read_csv(z.open('features.txt'),sep=',')
labels = pd.read_csv(z.open('target.txt'))
print (df.shape, labels.shape)
data_train = df.head(5413)
data_test = df.tail(1000)
label_train = labels.head(5413)
label_test = labels.tail(1000)
from sklearn.metrics import roc_curve, auc
from sklearn.metrics import roc_auc_score
def show_auc(d1, d2):
fpr, tpr, thresholds = roc_curve(d1,d2)
roc_auc = auc(fpr, tpr)
return 'AUC', roc_auc(6413, 122) (6413, 1)np.random.seed(0)
for epoch in [10,50,100,200]:
for batch_size in [1,10,100]:
w = train_sgd(np.array(data_train),labels=np.array(label_train),
lam=1, iter=epoch,batch_size=batch_size)
pred = predict(w, data_train.T)
score = show_auc(np.array(label_train.T)[0], pred[0])
print ('iter', epoch, 'batch', batch_size, 'egitim', score)
pred = predict(w, data_test.T)
score = show_auc(np.array(label_test.T)[0], pred[0])
print ('iter', epoch, 'batch', batch_size, 'test', score)iter 10 batch 1 egitim ('AUC', 0.8047518086158001)
iter 10 batch 1 test ('AUC', 0.7971786666666667)
iter 10 batch 10 egitim ('AUC', 0.7894177873794489)
iter 10 batch 10 test ('AUC', 0.7861306666666668)
iter 10 batch 100 egitim ('AUC', 0.7668542103627676)
iter 10 batch 100 test ('AUC', 0.7649733333333333)
iter 50 batch 1 egitim ('AUC', 0.7562366828358444)
iter 50 batch 1 test ('AUC', 0.7637626666666666)
iter 50 batch 10 egitim ('AUC', 0.794759653080582)
iter 50 batch 10 test ('AUC', 0.7964026666666666)
iter 50 batch 100 egitim ('AUC', 0.7577277052199766)
iter 50 batch 100 test ('AUC', 0.7551173333333333)
iter 100 batch 1 egitim ('AUC', 0.7847942568739994)
iter 100 batch 1 test ('AUC', 0.7882906666666667)
iter 100 batch 10 egitim ('AUC', 0.772609410468842)
iter 100 batch 10 test ('AUC', 0.7707013333333333)
iter 100 batch 100 egitim ('AUC', 0.7593143760002341)
iter 100 batch 100 test ('AUC', 0.7570266666666666)
iter 200 batch 1 egitim ('AUC', 0.7134575904456049)
iter 200 batch 1 test ('AUC', 0.7176400000000001)
iter 200 batch 10 egitim ('AUC', 0.7526888032672676)
iter 200 batch 10 test ('AUC', 0.7491333333333333)
iter 200 batch 100 egitim ('AUC', 0.7591727089662824)
iter 200 batch 100 test ('AUC', 0.757576)Hazır bir SVM kodu scikit-learn kütüphanesi karşılaştıralım,
from sklearn.svm import SVC
clf = SVC(kernel='linear',tol=0.1)
clf.fit(np.array(data_train),np.array(label_train))
pred = clf.predict(data_train)
print ('egitim',show_auc(np.array(label_train.T)[0], pred))
pred = clf.predict(data_test)
print ('test',show_auc(np.array(label_test.T)[0], pred))egitim ('AUC', 0.7690303271156629)
test ('AUC', 0.7533333333333333)Kaynaklar
[1] Blondel, https://gist.github.com/mblondel/586753
[2] Jebara, T., Machine Learning Lecture, Columbia University
[3] Song, et al., Stochastic gradient descent with differentially private updates
[4] Harrington, Machine Learning in Action
[5] Stanford, Stanford, CS246: Mining Massive Data Sets, http://web.stanford.edu/class/cs246/