En Dik İniş (Steepest Descent)

Daha önce gradyan inişi konusunda işlediğimiz üzere bir $f$ fonksiyonu için hesaplanan $-\nabla f(x)$ gradyanı $x$ noktasında fonksiyon için en yüksek iniş (descent) olacak yönü gösteriyordu [1, sf. 151]. Fakat dikkat, {\em yön} kelimesini kullandık, o yönde ne kadar adım atılacağını belirtmedik. Gradyanın temel hesabı türeve dayalı olduğu için ve türev hesapladığı noktaya yakın bir yerde doğru bir yaklaşıklama olacağı için o yönde atılan adımın büyüklüğüne göre minimizasyon iyi ya da kötü sonuçlar verebilir. Bu sebeple gradyan inişi algoritmaları, ki

$$ x^{x+1} = x^k + \alpha_k \nabla f(x^k) $$

ile kodlanırlar, çoğunlukla ufak ve pek çok adım atarlar, yani $\alpha_k$ sabitleri ufak seçilir. En Dik İniş (SD) algoritmasi bu noktada bir ilerleme. Her $\alpha$, yani $\alpha_k$ öyle seçilir ki $\phi(\alpha) \equiv f(x^k - \alpha \nabla f(x^k))$ kesinlikle minimize edilsin / belli bir yöndeki en minimum noktaya vardıracak büyüklükte adım atılsın. Ya da

$$ \alpha_k = \arg\min_{\alpha \ge 0} f(x^k - \alpha \nabla f(x^k)) $$

Yani gradyanın işaret ettiği yönde bir tür "arama" yapmış oluyoruz, adım büyüklüğünü öyle seçiyoruz ki fonksiyon o yönde o kadar adım atıldığında en fazla inişi gerçekleştirmiş olsun. Bu sebeple bu metota çizgi araması (line search) metotu deniyor.

Tabii arama derken akla ikinci bir döngü içinde yine ufak ufak adımlar atarak çizgi üzerinde gelinen yere bakıp büyüklük hesabını böyle yapmak gelebilir, bu sonuçsal olarak, kabaca doğru, ama asıl adım hesabı bazı cebirsel temellerle, ya da onu çözen yaklaşıksal şekilde yapılıyor.

En basiti atılan adım $\alpha$'yi pür cebirsel olarak çözmek, altta bir örnek [3, sf. 101].

Soru

$f(x) = 9x_1^2 + 4x_1x_2 + 7x_2^2$ fonksiyonunun optimal noktasını bul.

Çözüm

Gradyanın öğeleri

$\frac{\partial f}{\partial x_1} = 18 x_1 + 4x_2$ ve $\frac{\partial f}{\partial x_2} = 4 x_1 + 14 x_2$. Şimdi SD yöntemini uygulayalım, başlangıç noktası $x^0 = [\begin{array}{cc} 1 & 1 \end{array}]^T$ olsun. Bu durumda $f(x^0) = 20$, ve $\nabla f(x_0) = [\begin{array}{cc} 22 & 18 \end{array}]^T$. Adım denklemine göre,

$$ x^1 = x^0 - \alpha_0 \nabla f(x^0) $$

ya da

$$ \left[\begin{array}{c} x_1 \\ x_2 \end{array}\right] = \left[\begin{array}{c} 1 \\ 1 \end{array}\right] \alpha_0 \left[\begin{array}{c} 22 \\ 18 \end{array}\right] $$

Şimdi öyle bir $\alpha_0$ seçmeliyiz ki $f(x^1)$ minimum olsun. Üstteki değerlerin bize verdiği $x_1$ ve $x_2$ değerleri (ki $\alpha_0$ bazlı olacaklar) ana formüle yeni $x$ olarak sokarsak, $\alpha_o$ bazlı bir denklem edeceğiz,

$$ f(\alpha_0) = 20 - 808 \alpha_0 + 8208 (\alpha_0)^2 $$

$\frac{\mathrm{d} f(\alpha_0)}{\mathrm{d} \alpha_0} = 0$ üzerinden $\alpha_0$'nun optimum değeri $0.05$'tır. Yani adımı şu şekilde atmalıyız,

$$ x^1 = \left[\begin{array}{c} x_1 \\ x_2 \end{array}\right] = \left[\begin{array}{c} 1 \\ 1 \end{array}\right] 0.05 \left[\begin{array}{c} 22 \\ 18 \end{array}\right] $$

ki bu hesap bize $f(x^1) = 0.12$ verir. Bu şekilde özyineli döngüye devam edersek nihai optimum noktayı buluruz.

Sekant Yöntemi

Basit cebirsel numaralar ile üstte adımı bulduk. Daha çetrefil durumlar için sekant yöntemini kullanabiliriz. Bu yöntemi [2]'de işledik, ayrıca bkz [1, sf. 120]. Sonuçta aradığımız $d$ yönündeki minimum

$$ \phi_k(\alpha) = f(x^k + \alpha d^k) $$

değerini bulmaktır. Üstteki formülün $\alpha$ üzerinden türevi

$$ \phi_k'(\alpha) = {d^k}^T \nabla f(x^k + \alpha d^k) $$

O zaman minimum $\alpha$ icin

$$ 0 = {d^k}^T \nabla f(x^k + \alpha d^k) $$

denklemini çözen $\alpha$ gerekli. Bu bir kök bulma problemi ve sekant yöntemini kullanabiliriz.

def linesearch_secant(grad, d, x):
    epsilon=10**(-8)
    max = 500
    alpha_curr=0
    alpha=10**-8
    dphi_zero=np.dot(np.array(grad(x)).T,d)

    dphi_curr=dphi_zero
    i=0;
    while np.abs(dphi_curr)>epsilon*np.abs(dphi_zero):
        alpha_old=alpha_curr
        alpha_curr=alpha
        dphi_old=dphi_curr        
        dphi_curr=np.dot(np.array(grad(x+alpha_curr*d)).T,d)
        alpha=(dphi_curr*alpha_old-dphi_old*alpha_curr)/(dphi_curr-dphi_old);
        i += 1
        if (i >= max) and (np.abs(dphi_curr)>epsilon*np.abs(dphi_zero)):
            print('Line search terminating with number of iterations:')
            print(i)
            print(alpha)
            break

    return alpha

Örnek

$f(x_1,x_2,x_3) = (x_1 - 4)^4 + (x_2 - 3)^2 + 4(x_3 + 5)^4$ fonksiyonunun minimize edicisini bul.

Başlangıç noktamız $\left[\begin{array}{ccc} 4 & 2 & -1 \end{array}\right]^T$ olacak.

Üstteki fonksiyonun gradyanı

$$ \nabla f(x) = \left[\begin{array}{ccc}
4(x_1-4)^3 & 2(x_2-3) & 16(x_3+5)^3 \end{array}\right]^T $$

Kod olarak,

def g(x): return np.array([4*(x[0]-4)**3, 2*(x[1]-3), 16*(x[2]+5)**3])

$x^1$ hesaplamak için

$$ \alpha_0 = \arg\min_{\alpha \ge 0} f(x^0 - \alpha \nabla f(x^0)) $$

lazım, tam açılmış haliyle,

$$ = \arg\min_{\alpha \ge 0} (0 + (2+2\alpha-3)^2 + 4(-1-1024\alpha+5)^4 $$

Ama üstteki cebirle boğuşmaya gerek yok, gradyan fonksiyonu ve gidiş yönü üzerinden kök bulup bize döndürecek üstteki çizgi araması kodunu kullanabiliriz,

x0 = np.array([4,2,-1])
print (g(x0))
d0 = -g(x0)
alpha0 = linesearch_secant(g, d0, x0)
alpha0 = np.round(alpha0, 5)
print ('alpha0 =',alpha0)
x1 = x0 - alpha0*g(x0)
print ('x1',x1)

[   0   -2 1024]
alpha0 = 0.00397
x1 [ 4.       2.00794 -5.06528]

Arka arkaya iki adım daha atarsak,

print ('g1',g(x1))
d1 = -g(x1)
alpha1 = linesearch_secant(g, d1, x1)
print (alpha1)
x2 = x1 - alpha1*g(x1)
print ('x2',x2)
print ('\n')
print ('g2',g(x2))
d2 = -g(x2)
alpha3 = linesearch_secant(g, d2, x2)
print (alpha3)
x3 = x2 - alpha3*g(x2)
print ('x3',x3)

g1 [ 0.         -1.98412    -0.00445103]
0.5000022675782785
x2 [ 4.          3.0000045  -5.06305448]


g2 [ 0.00000000e+00  8.99829483e-06 -4.01113920e-03]
14.894217818923421
x3 [ 4.          2.99987048 -5.00331169]

Optimal noktaya erişmiş olduk.

Duruş Şartları

Optimizasyonda minimum varlığı için birinci-derecen gerekli şart (first-order necessary condition -FONC-) minimumda $\nabla f(x) = 0$ olması. Eğer böyle bir noktaya erişmişsek, diyelim $x^k$ için $\nabla f(x^k) = 0$ olmuş, bu nokta FONC'yi tatmin eder çünkü o zaman $x^{k+1} = x^k$ olur, ve minimumdayız demektir. Bu teorik bilgiyi algoritmamızın ne zaman duracağını anlaması için bir şart olarak kullanamaz mıyız?

Ne yazık ki sayısal hesaplarda, yani pratikte $\nabla f(x^k) = 0$ hesabı nadiren ortaya çıkar. Bir çözüm gradyanın normu $|| \nabla f(x) ||$ sıfır olmasına bakmak.

Ya da $| f(x^{k+1}) - f(x^k) |$ mutlak değerine bakmak, yani hedef fonksiyonun iki nokta arasındaki farkının mutlak değerine, bu değer eğer daha önceden belirlenmiş bir eşik değeri $\epsilon$'un altına düşmüşse durmak. Aynı şeyi $x^{n+1}$ ve $x^n$ değerlerinin kendisi için de yapabiliriz.

Fakat bu yöntemler ölçek açısından problemli olabilir. Mesela 1 ve 1000 arasında gidip gelen $f(x)$'lerle 0 ve 1 arasında gidip gelen $f(x)$'lerin kullanacağı $\epsilon$ farklı olabilir. Bir tanesi için $\epsilon = 100$ iyidir, diğeri için belki $\epsilon = 0.001$. Bu sebeple izafi bir hesap daha faydalı olur, mesela

$$ \frac{|f(x^{k+1} - f(x^k))|}{|f(x^k)|} < \epsilon $$

ya da

$$ \frac{||x^{k+1} - x^k||}{||x^k||} < \epsilon $$

Üstteki yaklaşım "ölçekten bağımsız" olduğu için daha tercih edilir yaklaşım, bir problemden diğerine geçtiğimizde farklı bir $\epsilon$ kullanmamız gerekmez.

Uygulama

Gradyan İnişi ve Model Uydurmak

Pek çok farklı probleme çözüm sağlayan bir teknik gradyan inişidir. Ne yazık ki bilgisayar bilim lisans seviyesinde bu teknik genellikle öğretilmiyor. Bu yazıda Gİ'nin hepimizin bildiği bir problemi, lineer regresyonu çözmek için nasıl kullanılacağını anlatacağım [1].

Teorik seviyede Gİ bir fonksiyonu minimize etmeye yarar. Elde bazı parametreler üzerinden tanımlı bir fonksiyon vardır, ve Gİ bir başlangıç değerinden başlayarak azar azar o parametreleri değiştirerek fonksiyonun minimal olduğu yeri bulmaya uğraşır. Bu azar azar, adım atılarak yapılan minimizasyon Calculus sayesindedir, fonksiyonun gradyanının negatif yönünde adım atılarak mümkün olur. Bazen bu matematiksel açıklamanın pratik kullanımı nasıl olur görmek zor oluyor; Örnek olarak bir veriye lineer bir çizgi / model uyduralım.

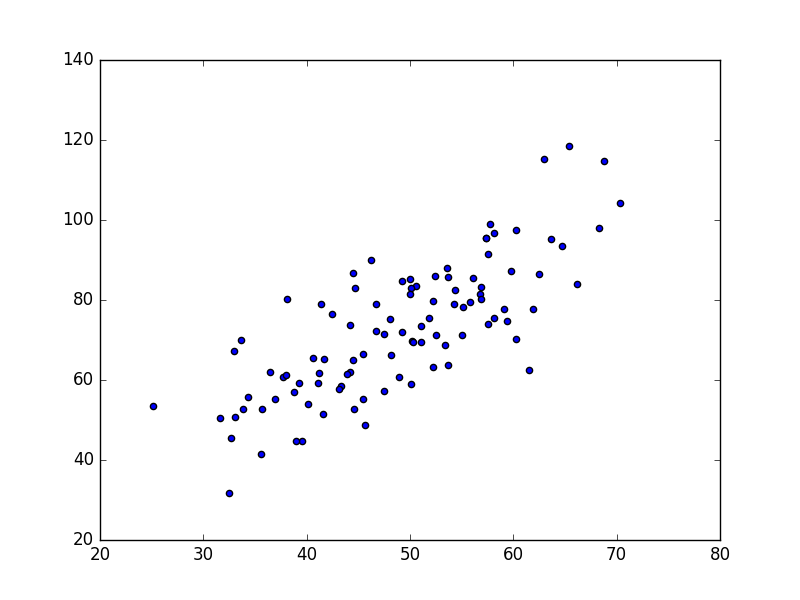
Basit bir tanım yaparsak lineer regresyonun amacı eldeki bir veri kümesine düz çizgi uydurmaktır. Veri alttaki gibi olabilir,

points = np.genfromtxt("data.csv", delimiter=",")
plt.scatter(points[:,0],points[:,1])
plt.savefig('vision_90fitting_04.png')

Üstteki veriyi düz çizgi olarak modellemek istiyoruz, bunun için lise matematiğinden bilinen $y = mx + b$ formülünü kullanacağız, $m$ eğim (slope), $b$ ise kesi (intercept), yani y-ekseninin kesildiği yer. Veriye uyan en iyi çizgiyi bulmak demek en iyi $m,b$ değerlerini bulmak demek.

Bunu yapmanının standart yolu bir hata fonksiyonu tanımlamak (bazen bedel fonksiyonu da deniyor). Hata fonksiyonu bir çizginin ne kadar "iyi" olduğunu ölçebilen bir fonksiyondur, bir $m,b$ çiftini alacak, veriye bakacak, ve bize uyumun ne kadar iyi olduğunu bir hata değeri üzerinden raporlayacak. Hata değeri hesabı için elimizdeki verideki tüm $x,y$ değerlerine bakacağız, ve bunu yaparken her veri $y$ değeri ile, yine veri $x$'i üzerinden hesapladığımız $mx+b$ değeri arasındaki farka bakacağız; daha doğrusu farkın karesini alacağız, ve her veri noktası için hesaplanan tüm bu kare hesaplarını toplayacağız. Kare alınıyor, çünkü bu hatayı pozitif hale çevirmemizi sağlıyor, bir diğer fayda tabii kare fonksiyonun türevi alınabilir olması (kıyasla mutlak değer fonksiyonu işleri daha karıştırırdı). Pozitif bir hata yeterli, çünkü hata yapılmışsa alttan mı üstten mi olduğu bizi ilgilendirmiyor. Hata $E$ hesabı şöyle,

Matematiksel olarak

$$ E_{(m,b)} = \frac{1}{N} \sum_{i=1}^{N} (y_i - (mx_i + b))^2$$

# y = mx + b
# m is slope, b is y-intercept
def compute_error_for_line_given_points(b, m, points):
    totalError = 0
    for i in range(0, len(points)):
        x = points[i, 0]
        y = points[i, 1]
        totalError += (y - (m * x + b)) ** 2
    return totalError / float(len(points))

Veriye daha iyi uyan çizgiler (ki "daha iyi"nin ne olduğu hata fonksiyonumuz üzerinden tanımlı) daha az hata değerleri anlamına gelecektir. O zaman, eğer hata fonksiyonunu minimize edersek, veriye uyan iyi çizgiyi bulacağız demektir. Hata fonksiyonumuz iki parametreli olduğu için onu iki boyutlu bir yüzey olarak grafikleyebiliriz,

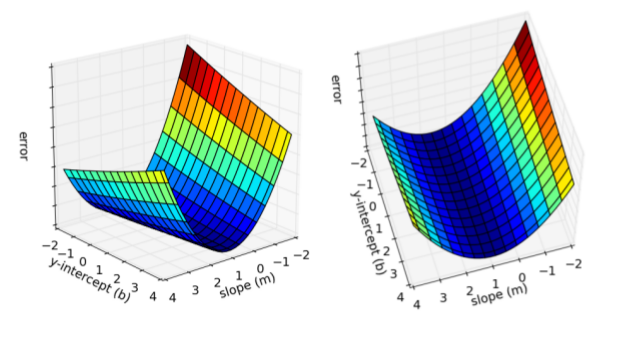
Bu iki boyutlu yüzey üzerindeki her nokta değişik bir çizgiyi temsil ediyor. Yüzeyin alt düzlemden olan yüksekliği o çizgiye tekabül eden hata. Gördüğümüz gibi bazı çizgiler bazılarından daha az hataya sahip (yani veriye daha iyi uymuş). Gradyan inişi ile arama yaptığımız zaman bu yüzeyin herhangi bir noktasından başlayacağız, ve yokuş aşağı inerek hatası en az olan çizgiyi bulacağız.

Hata fonksiyonu üzerinde Gİ işletmek için önce fonksiyonun gradyanını hesaplamamız lazım. Gradyan bizim için nerede olursak olalım her zaman dip noktasını gösteren bir pusula görevini görüyor. Gradyan hesabı için hata fonksiyonunun türevi alınmalı. Hata fonksiyonunun $m,b$ adında iki tane parametresi olduğuna göre bu iki parametrenin her biri için ayrı ayrı kısmi türev almamız lazım. Bu türevler,

$$ \frac{\partial E}{\partial m} = \frac{2}{N} \sum_{i=1}^{N} -x_i (y_i - (mx_i+b)) $$

$$ \frac{\partial E}{\partial b} = \frac{2}{N} \sum_{i=1}^{N} -(y_i - (mx_i+b)) $$

Artık Gİ işletmek için gerekli tüm araçlara sahibiz. Aramayı herhangi bir $m,b$ noktasından (herhangi bir çizgi) başlatırız, ve Gİ yokuş aşağı en iyi çizgi parametrelerine doğru gider. Her döngü $m,b$ değerlerini bu inişe göre günceller (dikkat inen parametreler değil, hatada inilirken bu inişe tekabül eden $m,b$ değerleri), ki bu sayede döngünün bir sonraki adımındaki hata bir öncekine göre azalmış olur.

Matematiğe biraz daha yakından bakalım [2]. Türev almak, türeve göre adım atmak bir fonksiyonunun minimum noktasını bulmamızı nasıl sağlıyor? Basit bir fonksiyon $f(x)$'i düşünelim,

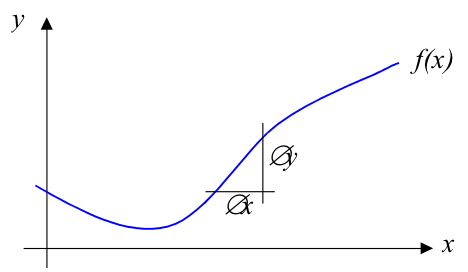
Gradyan, ya da belli bir $x$ noktasındaki değişim oranı $\oslash y / \oslash x$ ile yaklaşıksallanabilir (çoğunlukla literatur $\Delta$ sembolünü kullanır, [2] $\oslash$ kullanmış, önemli değil). Ya da bu yaklaşıksallığı şöyle yazabiliriz,

$$ \frac{\partial f}{\partial x} = \lim_{\oslash \to 0} \frac{\oslash y}{\oslash x} = \lim_{\oslash \to 0} \frac{f(x + \oslash x) - f(x)}{\oslash x} $$

ki bu ifade $f(x)$'in $x$'e göre kısmi türevi olarak bilinir. Üstteki yöntem ile sembolik olarak pek çok ifadenin türevini almayı biliyoruz, mesela $ax^2$ için $2ax$, vs.

Şimdi elimizde bir $f(x)$ olduğunu düşünelim, ve $x$'i öyle bir şekilde değiştirmek istiyoruz ki $f(x)$ minimize olsun. Ne yapacağımız $f(x)$'in gradyanının ne olduğuna bağlı. Üç tane mümkün durum var:

Eğer $\frac{\partial f}{\partial x} > 0$ ise $x$ artarken $f(x)$ artar, o zaman $x$'i azaltmalıyız.

Eğer $\frac{\partial f}{\partial x} < 0$ ise $x$ artarken $f(x)$ azalır, o zaman $x$'i arttırmalıyız.

Eğer $\frac{\partial f}{\partial x} = 0$ ise $f(x)$ ya minimum ya da maksimum noktasındadır, o zaman $x$'i olduğu gibi bırakmalıyız.

Özet olarak $x$'i alttaki miktar kadar azaltırsak $f(x)$'i de azaltabiliriz,

$$ \oslash x = x_{yeni} - x_{eski} = -\eta \frac{\partial f}{\partial x}$$

ki $\eta$ ufak bir pozitif sabittir, $x$'i değiştirirken bu atılan adımın büyüklüğünü dışarıdan ayarlayabilmemizi sağlar, değişimin hangi yönde olacağını $\frac{\partial f}{\partial x}$ belirtiyor zaten. Bu formülü ardı ardına kullanırsak, $f(x)$ yavaş yavaş minimum noktasına doğru "inecektir", bu yönteme gradyan inişi minimizasyonu adı verilmesinin sebebi de budur.

Örneğimize dönelim,

def step_gradient(b_current, m_current, points, eta):
    b_gradient = 0
    m_gradient = 0
    N = float(len(points))
    for i in range(0, len(points)):
        x = points[i, 0]
        y = points[i, 1]
        b_gradient += -(2/N) * (y - ((m_current * x) + b_current))
        m_gradient += -(2/N) * x * (y - ((m_current * x) + b_current))
    new_b = b_current - (eta * b_gradient)
    new_m = m_current - (eta * m_gradient)
    return [new_b, new_m]

eta = 0.0001
initial_b = 0 # initial y-intercept guess
initial_m = 0 # initial slope guess
num_iterations = 8
print "Starting gradient descent at b = {0}, m = {1}, error = {2}".format(initial_b, initial_m, compute_error_for_line_given_points(initial_b, initial_m, points))
print "Running..."
b = initial_b
m = initial_m
xx = np.linspace(np.min(points[:,0]),np.max(points[:,0]), 100)
for i in range(num_iterations):
    b, m = step_gradient(b, m, np.array(points), eta)
    if i % 2 == 0: 
        print i, b,m
        yy = m * xx + b
        plt.scatter(points[:,0],points[:,1])
        plt.hold(True)
        plt.scatter(xx,yy)
        plt.hold(False)
        plt.savefig('grad_desc_%d' % i)
print "After {0} iterations b = {1}, m = {2}, error = {3}".format(num_iterations, b, m, compute_error_for_line_given_points(b, m, points))    

Starting gradient descent at b = 0, m = 0, error = 5565.10783448
Running...
0 0.0145470101107 0.737070297359
2 0.0255792243213 1.29225466491
4 0.0284450719817 1.43194723238
6 0.029256114126 1.46709461772
After 8 iterations b = 0.0294319691638, m = 1.47298329822, error = 112.737981876

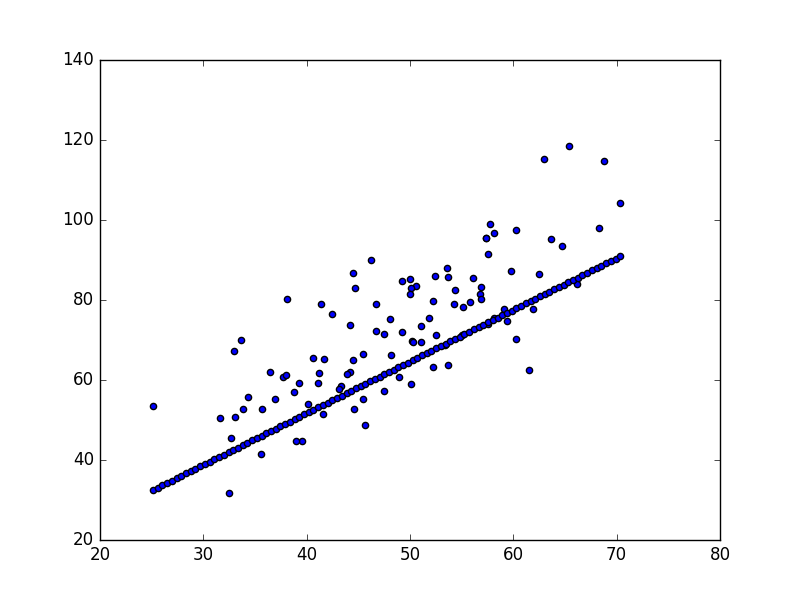
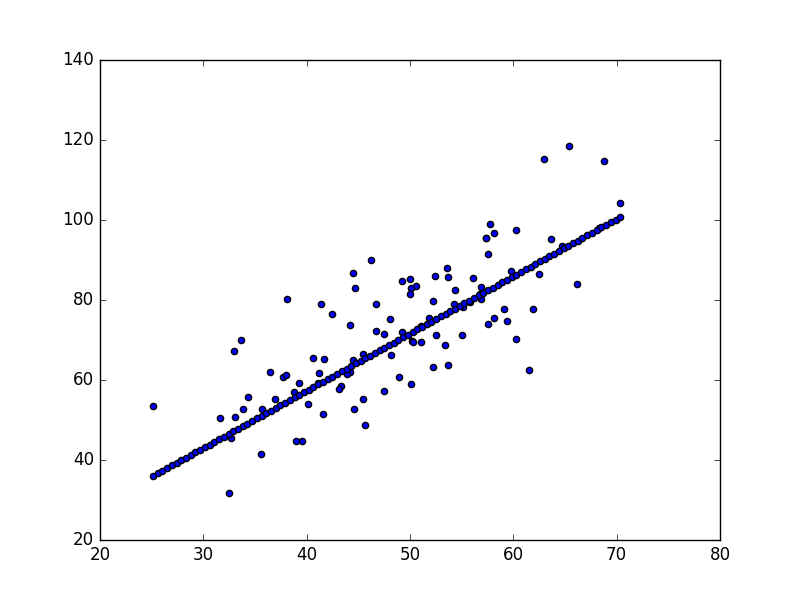
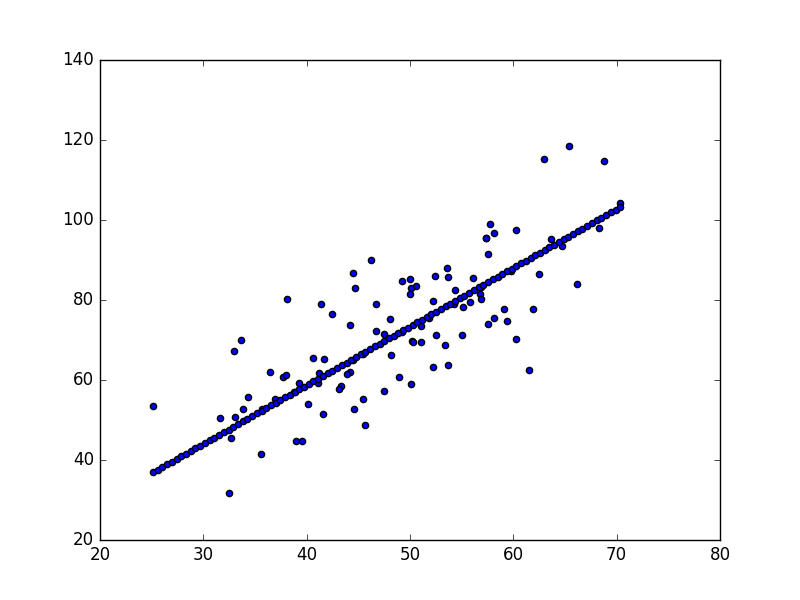
Optimal $m,b$ değerleri bulundu. $m=-1, b=0$'da başladık ve optimal sonucu bulduk. Değişken eta (yani $\eta$) adım büyüklüğü demiştik, dikkat eğer adım çok büyük seçilirse minimum "atlanabilir", yani varış noktası kaçırılabilir. Eğer $\eta$ çok küçük ise minimuma erişmek için çok vakit geçebilir. Ayrıca Gİ'nin doğru işlediğini anlamanın iyi yollarından birisi her döngüde hatanın azalıp azalmadığına bakmaktır.

Bu basit bir örnekti, fakat bir bedel fonksiyonunu minimize edecek parametre değişimlerini yapma kavramı yüksek dereceli polinomlarda, ya da diğer Yapay Öğrenim problemlerinde de işe yarıyor.

Gİ ile akılda tutulması gereken bazı konular:

1) Dışbükeylik (Convexity): Üstteki problemde sadece bir tane minimum vardı, hata yüzeyi dışbükeydi. Nereden başlarsak başlayalım, adım atarak minimuma erişecektik. Çoğunlukla durum böyle olmaz. Bazı problemlerde yerel minimumda takılı kalmak mümkün olabiliyor, bu problemleri aşmak için farklı çözümler var, mesela Rasgele Gradyan İnişi (Stochastic Gradient Descent) kullanmak gibi.

2) Performans: Örnekte basit bir Gİ yaklaşımı kullandık, çizgi arama (line search) gibi yaklaşımlarla döngü sayısının azaltmak mümkün olabiliyor.

3) Yakınsama (Convergence): Aramanın bittiğinin kararlaştırılmasını kodlamadık, bu çoğunlukla hata döngüsündeki değişimlere bakılarak yapılır; eğer hatadaki değişim belli bir eşik değerinden daha küçük ise, gradyanın sıfır olduğu yere yaklaşılmış demektir, ve arama durdurulabilir.

Not: Lineer regresyon tabii ki direk, tek bir adımda çözülebilen bir problem. Gİ'yi burada bir örnek amaçlı kullandık.

Kaynaklar

[1] Zak, An Introduction to Optimization, 4th Edition

[2] Bayramlı, Diferansiyel Denklemler, Kök Bulmak, Karesel Formül (Root Finding, Quadratic Formula)

[3] Dutta, Optimization in Chemical Engineering