SPH sıvıların dinamik hareketini görmemizi sağlayan bir simulasyon tekniğidir. Lagrangian bakış açısını temel alır, yani Euler aksine, bir sıvı paketini takip edip nereye gittiğine, hangi değişimlere uğradığına bakarız.
Önce akış dinamiğini formüllerini görelim,
Sıvının akışını simüle etmek pek çok alanda faydalı olabilecek bir tekniktir. Sıvıların kendisine ek olarak gazları yoğunluğu daha az olan sıvı olarak görebiliriz, hatta katı maddeler de akışkanlığı çok az sıvı gibi düşünülebilirse, böylece aerodinamikten başlayıp, gemi tasarlamaya, oradan oyunlarda duman simülasyonuna kadar giden geniş yelpazede teknikler kullanım bulabilir.
SPH tekniği bu sıvı simülasyon yöntemlerinden birisidir. Navier-Stokes denklemleri bir sıvının akışını tanımlar, bu denklem simülasyon ortamında yaklaşık olarak çözülmelidir [13], bunu yapmanın iki yolu vardır. Önceki anlatımdan hareketle herhalde cevabı tahmin edebiliriz, birisi Lagrange usulü diğeri Euler usulü. SPH yöntemi Lagrange yaklaşımını takip eder, yani bir sıvı paketini alıp onun zaman ve uzayda gidişini izler. Tek bir yere mıhlanmış olmamanın (Euler usulü) pek çok avantajları var, mesela oyun grafiklerini çizerken daha geniş bir alanda iş yapabilmek mümkün, farklı maddeler arasındaki iletişim daha rahat halledilebiliyor, vs.
Formülasyon için temel fizikle başlayalım. Simüle ettiğimiz bir sıvı paketidir demiştik, bu paketin ivmesini takip edelim mesela, bunun önemli olacagini tahmin edebiliriz, oradan kuvvet, enerji bağlantıları var, \(F=ma\) formülünden hareketle, ve materyel türev ile
\[ m \frac{D \bar{u}}{D t} = F^{toplam} \]
diyebiliriz. Daha önce materyel türevi yoğunluk üzerinde uygulamıştık, pek çok farklı ölçüt üzerinde materyel türev kullanılabilir demiştik, ayrıca hız \(\bar{u}\) materyel türev içinde kullanılmakta, ama hızın kendisine de gayet rahat bir şekilde materyel türev uygulanabilir.
Üstteki eşitliğin sağ tarafını detaylandırabiliriz, düşünelim, hangi kuvvetler bir sıvı akışı sırasında sıvı paketi / parçacık üzerinde etki ediyor? Bunlar sırasıyla basınç, ağdalık, ve yerçekim olurdu herhalde, bal gibi ağdalı bir sıvıda parçalar birbirlerine yapışkandır, şu için daha az, bu bir kuvvettir. Yerçekimi bir kuvvettir doğal olarak. Basınç ta öyle, biraz derine dalan herkes etrafındaki suyun basıncını bir kuvvet olarak hisseder. O zaman,
\[ m \frac{D \bar{u}}{D t} = F^{\textrm{basınç}} + F^{\textrm{ağdalık}} + F^{\textrm{yerçekim}} \]
diyebiliriz. Kuvvetlerden en basiti yerçekimi, \(F^{\textrm{yerçekim}} = m \bar{g}\). İvme \(\bar{g}\) bir vektör olarak gösterildi, bu \(\bar{g} = (0, 0, 9.8)\) olurdu, sadece z ekseni üzerinde etki eden bir ivmelenme yani.
Diğer kuvvet basınç. Yüksek basınç bölgeleri alçak basınç bölgelerinde doğru bir kuvvet uygular. Basıncın tüm sıvı için \(p(\bar{x})\) değişkeninde olduğunu düşünelim, peki basınç dengesizliğini matematiksel olarak göstermenin en basit yolu nedir? Basıncın negatif gradyanını almak, \(-\nabla p\) olur mu acaba? Evet. Temel Calculus’tan hatırlarsak gradyan en dik iniş yönünü gösterir, o zaman gradyanın negatifi yüksek basınç bölgesinden dışarı, alçak basınç bölgesine doğru gösterecektir. Tabii ki bu etkiyi üzerinde olduğumuz sıvı paketinin hacmi üzerinden entegre etmemiz gerekir, ama basit bir yaklaşıklama olarak onu direk hacim \(V\) ile çarpabiliriz. Tümü \(F^{\textrm{basınç}} = - V \nabla p\).
Üçüncü kuvvet ağdalık. Ağdalı bir sıvı deforme edilmeye karşı direnir. Bu kuvveti kabaca “her parçacığı yanındaki diğer parçacıkların ortalama hızında hareket etmesini zorlayan kuvvet’’ olarak görebiliriz, bir diğer deyişle birbirine yakın olan parçacıkların arasındaki hız farklarını minimize etmeye uğraşan kuvvet. Şimdi, mesela görüntü işleme literatürünü düşünürsek, o alanda çalışanlar bir ölçünün etrafındaki ortalamadan ne kadar saptığını hesaplamak için bir diferansiyel operatör kullanır, bu operatör Laplasyan \(\nabla \cdot \nabla\). Bu operatör, aynı şekilde hacim üzerinden entegre edilince bize ağdalık kuvvetini verebilir, burada bir ek her sıvının farklı ağdalığını formüle dahil edebilmek için bir de bir dinamik ağdalık sabiti (dynamic viscosity coefficient) \(\mu\) ile herşeyi çarpmak gerektiği, o zaman \(F^{\textrm{ağdalık}} = V \mu \nabla \cdot \nabla \bar{u}\) formülünü elde ediyoruz.
Hepsini bir araya koyunca,
\[ m \frac{D \bar{u}}{D t} = m\bar{g} - V \nabla p + V \mu \nabla \cdot \nabla \bar{u} \]
Bu denklemi hacim ve kütle limite giderken düşüneceğiz, ama bu haliyle formül problem çıkartabilir, o zaman her şeyi \(V\) ile bölersek ve sonra limiti düşünürsek daha iyi olur, \(m/V\)’yi sıvı yoğunluğu \(\rho\) olarak tanımlayalım,
\[ \rho \frac{D \bar{u}}{D t} = \rho \bar{g} - \nabla p + \mu \nabla \cdot \nabla \bar{u} \]
Bu denklem bazıları için tanıdık gelebilir.. Navier-Stokes denklemine benzemiyor mu? Navier-Stokes ünlü denklemi,
\[ \frac{\partial \bar{u}}{\partial t} + \bar{u} + \frac{1}{\rho} \nabla p = \bar{g} + \nu \nabla \cdot \nabla \bar{u} \]
\[ \nabla \cdot \bar{u} = 0 \]
olarak gösterilir.
Neyse bizim türetişle devam edersek, her şeyi yoğunluk \(\rho\) ile bölelim,
\[ \frac{D \bar{u}}{D t} + \frac{1}{\rho} \nabla p = \bar{g} + \frac{\mu}{\rho} \nabla \cdot \nabla \bar{u} \]
Basitleştirme amacıyla kinematik ağdalık \(\nu = \mu / \rho\) tanımlayalım, o zaman
\[ \frac{D \bar{u}}{D t} + \frac{1}{\rho} \nabla p = \bar{g} + \nu \nabla \cdot \nabla \bar{u} \]
Sıkıştırılamazlığın (incompressibility) \(\nabla \cdot \bar{u} = 0\) olduğunu daha önce [5]’deki (2) formülünde görmüştük.
Devam edelim,
\[ \rho \frac{D \bar{u}}{D t} = F^{toplam} \]
denklemini gördük. Bu Newton’un \(F=ma\) formülasyonun bir karşılığı. Bu denklemde basınç, ağdalık gibi kuvvetler için terimler vardı. Toplam kuvvetleri açarsak,
\[ F^{toplam} = F^{\textrm{basınç}} + F^{\textrm{ağdalık}} + F^{\textrm{yerçekim}} \]
Daha detaylı hali,
\[ \rho \frac{D \bar{u}}{D t} = - \nabla p + \mu \nabla \cdot \nabla \bar{u} + \rho \bar{g} \qquad (1) \]
Simulasyon için bize ivme gerekli. Kütle ve kuvvetten ivme, oradan sayısal entegrasyon ile yer değişimi elde edilebilir, katı-gövde simulasyonunu kodlarken [6]’da bu anlatılmıştı. O zaman eldeki \(i\)’inci parçacık için toplam kuvvet \(F_i\) hesaplarsak
\[ a_i = \frac{\mathrm{d} u_i}{\mathrm{d} t} = \frac{F_i}{\rho_i} \]
ile ivmeyi buluruz, ve oradan devam ederiz.
Şimdi bize gereken \(\nabla p(r_i)\) ve \(\nabla^2 u(r_i)\) hesaplarını yaklaşık yapabilmemizi sağlayacak bir metot kullanmak. SPH tekniği bunu sağlıyor.
Bir fonksiyon \(A\) aradeğerleme (interpolation) / yaklaşıklama üzerinden temsil edilebilir [1],
\[ A_I(r) = \int A(r') W(r-r',h) \mathrm{d} r' \]
Belirtilmediği yerlerde \(r = \bar{r}\), \(u = \bar{u}\) kabul edilebilir, bunlar vektör, \(\mathrm{d} r'\) diferansiyel hacim öğesi. \(A_I\) aradeğerlenmiş fonksiyon, \(A\) yaklaşık göstermeye uğraştığımız fonksiyon. \(A\) simulasyon ortamında hesaplanan herhangi bir ölçüt olabilir, mesela herhangi bir \(r=(x,y,z)\) noktasındaki basınç, sıcaklık, yoğunluk, vs.
\(W\) ağırlık fonksiyonudur, ya da çekirdek (kernel) fonksiyonu, sahip olması gereken bir şart,
\[ \int_\Omega W(r-r',h) \mathrm{d} r' = 1 \]
ve
\[ \lim_{h \to 0} W(r,h) = \delta(r) \]
[4, sf. 11]. [4]’te bu tekniğin Dirac fonksiyonu ile bağlantıları anlatıldı. Eğer \(W = \delta\) dersek, yani çekirdek için Dirac fonksiyonu kullanırsak, orijinal fonksiyonun kendisini elde ederiz.
SPH’in temel fikri entegral aradeğerlemeden geliyor, hatta ona bir tür Çekirdek Yoğunluk Kestirme (Kernel Density Estimation) yöntemi de denebilir. Sıvıyı ayrıksal parçalara bölüyoruz, ve takip edilen ölçüt ne ise çekirdek fonksiyonu üzerinden bu ölçüt pürüzsüzleştiriliyor / etrafa yayılıyor / yumuşatılıyor. Yani çekirdek yarıçapı içindeki diğer parçacıklar o an üzerinde olduğumuz parçacığın neyini ölçüyorsak onu etkiliyor, mesela yakındaki parçacıkların basıncı ya da yoğunluğu bizim basıncı, yoğunluğu etkiliyor. Kabaca düşünülünce aslında bu bakış açısının sıvıların tabiatına son derece uygun olduğu anlaşılacaktır.
Ortalamanın alınma şekli RBF tekniği [11] ile ya da olasılıktaki beklenti hesabına benziyor, RBF ile üzerinde olduğumuz veriyi etraftaki verilere Gaussian uydurarak temsil etmeye uğraşırız, SPH ile üzerinde olduğumüz parçacık ölçümünü etraftaki ölçütlerin (çoğunlukla Gaussian-ımsı) bir çekirdek üzerinden ortalamasıyla temsil ederiz. Ortalama bir entegraldir, Olasılık Teorisi’nde beklentinin alınması gibi, \(x\) değerlerinin \(f(x)\) üzerinden ağırlıklı ortalaması \(\int_{\-infty}^{\infty} x f(x) \mathrm{d} x\).
Yaklaşıklamayı sıvıya uygulamak için onu kütle öğelerine bölmemiz gerekli, \(i\)’inci öğe \(m_i\) kütlesine, \(\rho_i\) yoğunluğuna, ve \(r_i\) pozisyonuna sahip olacak. \(A\) ölçütü / hesabının \(i\) parçacığındaki değeri \(A_i\) ile gösterilsin. Her parçacık için,
\[ A(r) = \int A(r') W(r-r',h) \mathrm{d} r' \]
Yaklaşıklık için \(A_I(r)\) da diyebilirdik, ya da \(\approx\) kullanabilirdik. Şimdi,
\[ = \int \frac{A(r')}{\rho(r')} W(r-r',h) \rho(r') \mathrm{d} r' \]
\(\rho(r')\)’i hem bölen hem bölünene eklediğimiz için hiçbir değişim yaratmamış olduk, ama böylece \(\rho(r') \mathrm{d} r'\) ifadesi elde ettik ki ona parçacık kütlesi diyebiliriz. Böylece parçacıkların kütleleri üzerinden bir toplam alabiliriz,
\[ A_s(r) = \sum_b m_b \frac{A_b}{\rho_b} W(r-r_b, h) \]
Formülde kütle kullanımı daha faydalı çünkü kütle simülasyona başlamadan önce bilinir, hatta çoğu parçacık için birbirinin aynısıdır.
Üstteki toplamın teoride tüm parçacıklar üzerinden alındığı gösterildi, fakat pratikte \(r\)’ye yakın olan diğer parçacıklar üzerinden alınır, çoğunlukla çekirdek \(2h\) gibi bir uzaklıkta zaten hızla sıfıra düştüğü için, ayrıca performans açısından, çok uzaktaki parçacıkları göz önüne almaya gerek yoktur.
Bu formül bana herhangi bir \(r\) noktasında hesaplayabileceğim bir \(A\) kestirme hesabı (estimation) vermiş oldu. Parcaçık bazlı simulasyon yaptığımız için her \(i\) parçacığı çevresindeki \(j\) parçacıkları üzerinden bu kestirme hesabı yapabileceğiz.
Bazı hesaplar formülün basit yan ürünü, mesela yoğunluk
\[ \rho_i = \rho(r_i) = \sum_j m_j \frac{\rho_j}{\rho_j} W(r_i-r_j, h) = \sum_j m_j W(r_i-r_j, h) \]
Yani etraftaki parçacıkların kütlesi üzerinden alınan bir ağırlıklı ortalama bana parçacığın yoğunluğunu veriyor.
Aradeğerlemenin bize sağladığı güzel bir özellik onun üzerinden mesela kolayca gradyan alabilmem. Diyelim ki \(A\) ölçümü basınç, yani \(p\). O zaman (1)’de görülen \(-\nabla p\) formülünü üstteki entegral üzerinden açabilmem gerekir (\(p\) ölçümünün ya da hesabının nereden geldiği ileride anlatılacak). \(r\)’de olan her \(i\) parçacığı için \(p(r_i)\) diyelim,
\[ p(r_i) = \sum_j \frac{m_j p_j}{\rho_j} W(r_i-r_j,h) \]
Bu denklemin gradyanını alabiliriz şimdi,
\[ \nabla p(r_i) = \sum \frac{m_j p_j}{\rho_j} \nabla W(r_i-r_j,h) \]
Gradyan direk \(W\) üzerinde uygulanmış oldu. Burada modellemeyi yapan kişi tabii ki \(W\)’yi “gradyanı rahat alınan’’ fonksiyonlar arasından da seçecektir, böylece işi daha kolaylaşacaktır.
O zaman üstteki sonuç ile \(-\nabla p\) yazarsak,
\[ F_i^{\textrm{basınç}} = - \sum_j \frac{m_j p_j}{\rho_j} \nabla W(r_i-r_j,h) \]
elde ederiz.
Yanlız burada bir problem var, \(j\) bölgesindeki basıncı kullanarak o fark üzerinden \(i\) üzerindeki kuvveti hesapladık, fakat basınç farkı dolayısıyla \(i\)’nin \(j\) üzerinde uyguladığı kuvvet aynı olmayabilir. Yani kuvvet simetrik olmaz, fakat fizik kanunlarına göre etki-tepki aynı olmalıdır. Simulasyon amacıyla çoğunlukla yapılan dışarıdan müdahele ile kuvveti simetrik hale getirmektir, mesela bir yöntem basit aritmetik ortalama almak,
\[ F_i^{\textrm{basınç}} = - \nabla p(r_i) = - \sum_j m_j \frac{p_i + p_j}{2 \rho_j} \nabla W(r_i-r_j,h) \]
Ağdalık kuvvetine gelelim. İlk başta (1) bazlı olarak bu formül
\[ F_i^{\textrm{ağdalık}} = \mu \sum_j m_j \frac{u_j}{\rho_j} \nabla^2 W (r_i-r_j, h) \]
olarak yazılabilirdi. Fakat simetriklik problemi burada da var, bu problem de hıza olan bağlantıyı izafi hıza çevirerek çözülebilir, çünkü fiziksel olarak düşünülürse esas önemli olan mutlak hızlar değil iki parçacığın hızlarının farkı, ya da bir parçacığın diğerine baktığında gördüğü hız (ki bu izafi demek) o zaman
\[ F_i^{\textrm{ağdalık}} = \mu \sum_j m_j \frac{u_j-u_i}{\rho_j} \nabla^2 W (r_i-r_j, h) \]
daha uygun olur.
Çekirdek Fonksiyon Seçimi
SPH’in stabilitesi, doğruluğu ve hesap hızı pürüzleştirme
çekirdeğinin doğru seçilmiş olmasına bağlı [2]. Çekirdek fonksiyonlarını
hangisinin, hangi durumlarda iyi olacağı aktif bir araştırma alanıdır.
Yaygın kullanılan bir çekirdek poly6 ismiyle bilinen 6.
derece polinom çekirdeği. Bu fonksiyon,
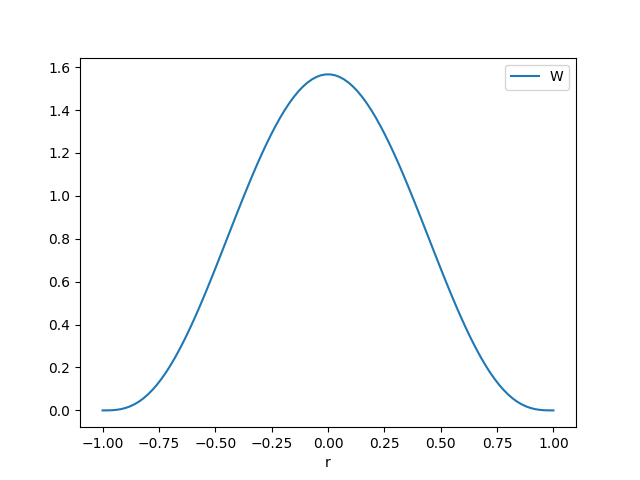
\[ W_{poly6} (r, h) = \frac{315}{64 \pi h^9} \left\{ \begin{array}{ll} (h^2 - ||r||^2)^3 & 0 \le ||r|| \le h \\ 0 & ||r|| > h \end{array} \right. \]
Gradyanı,
\[ \nabla W (r, h) = - \frac{945}{32 \pi h^9} r ( h^2 - ||r||^2)^2 \]
Laplasyanı ise,
\[ \nabla^2 W (r, h) = - \frac{945}{32\pi h^9} (h^2 - ||r||^2)(3 h^2 - 7||r||^2) \]
Tek boyutta ve \(h=1\) üzerinden her üç fonksiyonu grafikleyebiliriz,
r = np.linspace(-1,1,100)
h = 1
import pandas as pd
df = pd.DataFrame(r)
df.columns = ['r']
df['W'] = (315./(64*np.pi*h**9)) * (h**2 - np.abs(r)**2)**3
df = df.set_index('r')
df.plot()
plt.savefig('compscieng_app40sph_01.png')
df = pd.DataFrame(r)
df.columns = ['r']
df['W'] = (315./(64*np.pi*h**9)) * (h**2 - np.abs(r)**2)**3
df['Gradyan W'] = -945./(32*np.pi*h**9) * r * (h**2 - np.abs(r)**2)**2
df = df.set_index('r')
df.plot()
plt.savefig('compscieng_app40sph_02.png')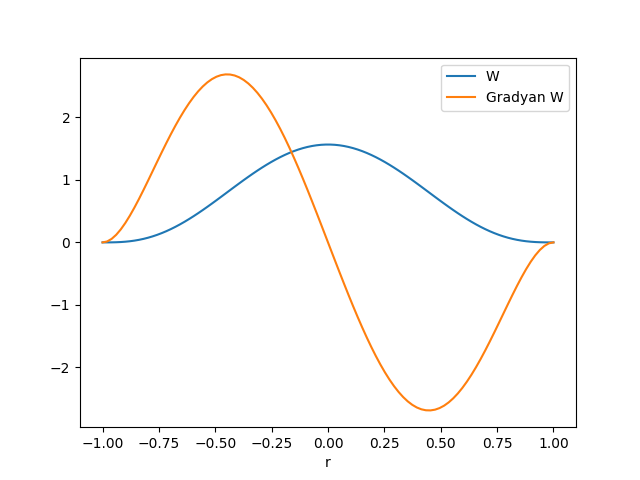
df = pd.DataFrame(r)
df.columns = ['r']
df['W'] = (315./(64*np.pi*h**9)) * (h**2 - np.abs(r)**2)**3
df['Gradyan W'] = -945./(32*np.pi*h**9) * r * (h**2 - np.abs(r)**2)**2
df['Laplasyan W'] = -945./(32*np.pi*h**9) * \
(h**2-np.abs(r)**2) * \
(3*h**2 - 7**np.abs(r)**2)
df = df.set_index('r')
df.plot()
plt.savefig('compscieng_app40sph_03.png')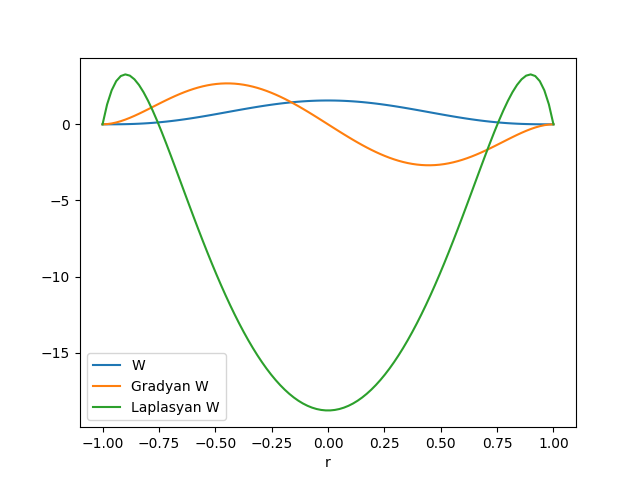
Basınç
Basınç kuvveti eğer basınç biliniyorsa hesaplanabilir, basıncın kendisini hesaplamak için İdeal Gaz Kanunu gerekli [9], bu kanun
\[ p V = n R T \]
ki \(V = 1 / \rho\), yani birim kütleye düşen hacim, \(n\) mol üzerinden kaç tane gaz parçacığı olduğu, \(R\) evrensel gaz sabiti, \(T\) ise sıcaklık. SPH için sıvıda eşsıcaklık (isothermal), ve parçacıkların sayısı simulasyon sırasında değişmez kabul edilir, o zaman üstteki formülün sağ tarafında bir gaz sertlik (stiffness) sabiti \(k\) kullanılabilir [4, sf. 18],
\[ p V = k \]
\[ p \frac{1}{\rho} = k \]
\[ p = k \rho \]
Sayısal kodlamalarda stabilite amaçlı olarak ayrıca bir de \(\rho_0\) kullanılır, ki her basınç hesabı için yoğunluğun bu baz \(\rho_0\) ile olan farkı bazlı alınır, nihai formül,
\[ p = k (\rho - \rho_0) \]
Simülasyon kodu alttadır. Simüle edilen bir blok sıvıyı havada asılı bir durumdan bırakmak. Ne olacak? Yerçekim etkisiyle tabii ki sıvı parçacıkları düşmeye başlayacaklar, ama normal sadece elastik çarpışma içeren simülasyondan farklı olarak şimdi sıvı parçacıkları arasında ağdalık var, yani birbirlerine yakın durmaya meyilliler. Ayrıca basınç var, tüm bunların etkisini simüle eden program acaba sıvısal bir davranış gösterecek mi? Simülasyon animasyon / video olarak [10]’da bulunabilir.
from random import random
from collections import defaultdict
import numpy as np, datetime
import sys, numpy.linalg as lin
from mayavi import mlab
import itertools
m = 0.1
R = 0.1
EPS = 0.1
BOUND_DAMPING = -0.6
mmin,mmax=0.0,2.0
BN = int(np.abs(mmax-mmin) / R) + 1
bins = np.linspace(mmin, mmax, BN)
G = np.array([0.0, 0.0, -9.8*2])
REST_DENS = 10.0
GAS_CONST = 0.5
MASS = 100.0
VISC = 20.0
DT = 0.1
H = 0.1 # kernel radius
PI = 3.14159
HSQ = H*H # radius^2 for optimization
POLY6 = 315.0/(65.0*PI*np.power(H, 9.));
SPIKY_GRAD = -45.0/(PI*np.power(H, 6.));
VISC_LAP = 45.0/(PI*np.power(H, 6.));
EPS = 0.05
BOUND_DAMPING = -0.5
idx27 = list(itertools.product( [-1,0,1], repeat=3 ))
class Simulation:
def __init__(self):
self.r = R
self.balls = []
def init(self):
i = 0
for xs in np.linspace(0, 0.4, 10):
for ys in np.linspace(0, 0.4, 10):
for zs in np.linspace(0, 0.4, 10):
v = np.array([0.0, 0.0, 0.0])
f = np.array([0,0,0])
x = np.array([xs, ys, zs])
xi = np.digitize(xs, bins)
yi = np.digitize(ys, bins)
zi = np.digitize(zs, bins)
d = {'x': x, 'f':f, 'v': v, 'i': i, 'rho': 0.0, 'p': 0.0, 'grid': (xi,yi,zi)}
self.balls.append(d)
i += 1
self.rvec = np.ones(i) * self.r
def get_neighbors(self, ball):
neighbors = {}
cx,cy,cz = ball['grid']
for (xa,ya,za) in idx27:
nx,ny,nz = cx+xa,cy+ya,cz+za
if (nx,ny,nz) in self.grid_hash:
tn = self.grid_hash[(nx,ny,nz)]
for n in tn: neighbors[ n['i'] ] = n
return neighbors
def hash_balls(self):
self.grid_hash = defaultdict(list)
for i,b in enumerate(self.balls):
xi = np.digitize(b['x'][0], bins)
yi = np.digitize(b['x'][1], bins)
zi = np.digitize(b['x'][2], bins)
b['grid'] = (xi,yi,zi)
self.grid_hash[(xi,yi,zi)].append(b)
def computeDensityPressure(self):
for i,pi in enumerate(self.balls):
pi['rho'] = 0.0
otherList = self.get_neighbors(pi)
for (k,pj) in otherList.items():
r2 = lin.norm(pj['x']-pi['x'])**2
if r2 < HSQ:
pi['rho'] += MASS*POLY6*np.power(HSQ-r2, 3.0)
pi['p'] = GAS_CONST*(pi['rho'] - REST_DENS)
def computeForces(self):
for i,pi in enumerate(self.balls):
fpress = np.array([0.0, 0.0, 0.0])
fvisc = np.array([0.0, 0.0, 0.0])
otherList = self.get_neighbors(pi)
for k,pj in otherList.items():
if pj['i'] == pi['i']: continue
rij = pi['x']-pj['x']
r = lin.norm(rij)
if r < H:
if np.sum(rij)>0.0: rij = rij / r
tmp1 = -rij*MASS*(pi['p'] + pj['p']) / (2.0 * pj['rho'])
tmp2 = SPIKY_GRAD*np.power(H-r,2.0)
fpress += (tmp1 * tmp2)
tmp1 = VISC*MASS*(pj['v'] - pi['v'])
tmp2 = pj['rho'] * VISC_LAP*(H-r)
fvisc += (tmp1 / tmp2)
fgrav = G * pi['rho']
pi['f'] = fpress + fvisc + fgrav
def integrate(self):
for j,p in enumerate(self.balls):
if p['rho'] > 0.0:
p['v'] += DT*p['f']/p['rho']
p['x'] += DT*p['v']
if p['x'][0]-EPS < 0.0:
p['v'][0] *= BOUND_DAMPING
p['x'][0] = 0.0
if p['x'][0]+EPS > 2.0:
p['v'][0] *= BOUND_DAMPING
p['x'][0] = 2.0-EPS
if p['x'][1]-EPS < 0.0:
p['v'][1] *= BOUND_DAMPING
p['x'][1] = 0.0
if p['x'][1]+EPS > 2.0:
p['v'][1] *= BOUND_DAMPING
p['x'][1] = 2.0-EPS
if p['x'][2]-EPS < 0.0:
p['v'][2] *= BOUND_DAMPING
p['x'][2] = 0.0
if p['x'][2]+EPS > 2.0:
p['v'][2] *= BOUND_DAMPING
p['x'][2] = 2.0-EPS
self.hash_balls()
def update(self):
self.hash_balls()
self.computeDensityPressure()
self.computeForces()
self.integrate()
def display(self, i):
mlab.options.offscreen = True
ball_vect = [[b['x'][0],b['x'][1],b['x'][2]] for b in self.balls]
ball_vect = np.array(ball_vect)
fig = mlab.figure(figure=None, fgcolor=(0., 0., 0.), bgcolor=(1, 1, 1), engine=None)
color=(0.2, 0.4, 0.5)
mlab.points3d(ball_vect[:,0], ball_vect[:,1], ball_vect[:,2], self.rvec, color=color, colormap = 'gnuplot', scale_factor=1, figure=fig)
mlab.points3d(0, 0, 0, 0.1, color=(1,0,0), scale_factor=1.0)
BS = 2.0
mlab.plot3d([0.0,0.0],[0.0, 0.0],[0.0, BS], color=(0,0,0), tube_radius=None, figure=fig)
mlab.plot3d([0.0,BS],[0.0, 0.0],[0.0, 0.0], color=(1,0,0), tube_radius=None, figure=fig)
mlab.plot3d([0.0,0.0],[0.0, BS],[0.0, 0.0], color=(0,1,0), tube_radius=None, figure=fig)
mlab.plot3d([0.0,0.0],[0.0, BS],[BS, BS], color=(0,0,0), tube_radius=None, figure=fig)
mlab.plot3d([0.0,BS],[0.0,0.0],[BS,BS], color=(0,0,0), tube_radius=None, figure=fig)
mlab.plot3d([BS,BS],[0.0,BS],[BS,BS], color=(0,0,0), tube_radius=None, figure=fig)
mlab.plot3d([BS,0],[BS,BS],[BS,BS], color=(0,0,0), tube_radius=None, figure=fig)
mlab.plot3d([0,0],[BS,BS],[BS,0], color=(0,0,0), tube_radius=None, figure=fig)
mlab.plot3d([BS,BS],[0.0,0.0],[0.0,BS], color=(0,0,0), tube_radius=None, figure=fig)
mlab.plot3d([BS,BS],[0.0,BS],[0.0,0.0], color=(0,0,0), tube_radius=None, figure=fig)
mlab.plot3d([BS,0.0],[BS,BS],[0.0,0.0], color=(0,0,0), tube_radius=None, figure=fig)
mlab.plot3d([BS,BS],[BS,BS],[0.0,BS], color=(0,0,0), tube_radius=None, figure=fig)
mlab.view(azimuth=50, elevation=80, focalpoint=[1, 1, 1], distance=8.0, figure=fig)
mlab.savefig(filename='/tmp/sim/out-%02d.png' % i)
if __name__ == '__main__':
s = Simulation()
s.init()
for i in range(20):
print (i)
s.update()
s.display(i)
#exit()
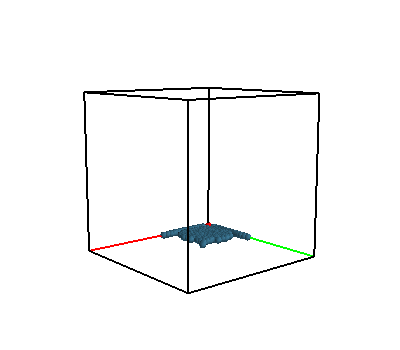
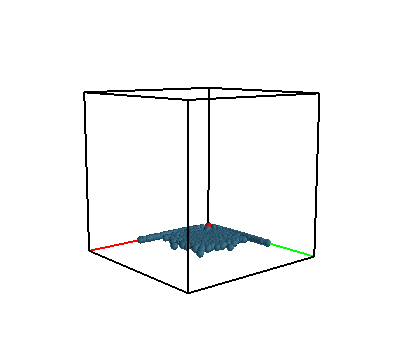

Komşuları bulmak için [12]’deki ızgara bazlı yöntem kullanıldı. Bu yöntem, biraz ek yapılarak mükkemmel sonuç verebilir, ve bu önemli çünkü SPH’in doğru çalışabilmesi için tüm komşuların bulunabilmesi gerekir.
Kaynaklar
[1] Monaghan, Smoothed particle hydrodynamics, 2005
[2] Schuermann, Particle-Based Fluid Simulation with SPH, https://lucasschuermann.com/writing/particle-based-fluid-simulation
[3] Bayramlı, Hesapsal Bilim, Ders 4
[4] Kelager, Lagrangian Fluid Dynamics Using Smoothed Particle Hydrodynamics
[5] Bayramlı, Fizik, Muhafaza Kanunları
[6] Bayramlı, Fizik, Simulasyon
[7] Monaghan, Introduction to SPH Part I, https://www.youtu.be/tAXHCAEgSuE
[8] Müller, Particle-Based Fluid Simulation for Interactive Applications
[9] Bayramlı, Fizik, Temel Fizik 3, Basınç, Çarpışma
[10] Bayramlı, Simulasyon Animasyonu, https://github.com/burakbayramli/classnotes/blob/master/compscieng/compscieng_app40sph/balls4.gif?raw=true
[11] Bayramlı, Istatistik, Dairesel Baz Fonksiyonları (Radial Basis Functions -RBF-)
[12] Bayramlı, Bilgisayar Bilim, Geometrik Anahtarlama (Spatial Hashing) ve Izgara (Grid) ile En Yakın Noktaları Bulmak
[13] Schuermann, Particle-Based Fluid Simulation with SPH, https://lucasschuermann.com/writing/particle-based-fluid-simulation