dersblog



Katı-Gövde Simülasyonu

Dönüş Animasyonu

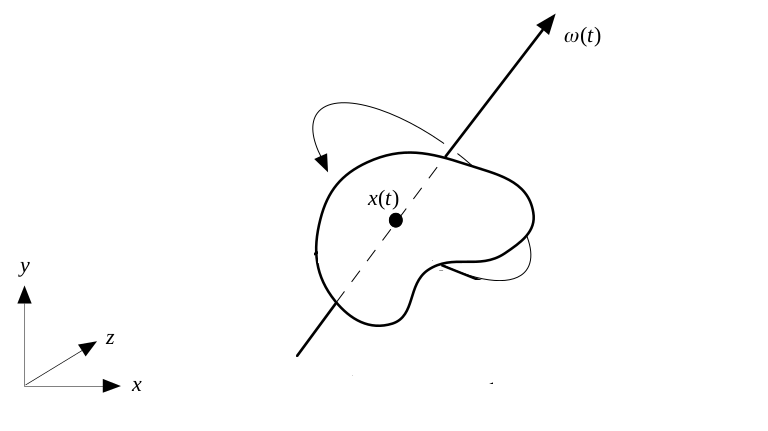
Bir örnek gövde üzerinde simülasyon yapmaya uğraşalım. Elimizde bir simit, ya da geometride torus denen bir şekil var. Bu dosya STL denen bir format içinde, detaylar için [1]. Kuvvet uygulama sonrası lineer ve açısal momentum içeren simülasyon için pek çok değişkeni diferansiyel tanımları üzerinden entegre etmemiz gerekiyor, daha basit bir örnek ile, özellikle sabit bir açışal hız üzerinden salt döndürme ile başlamak uygun olabilir. [4]'te tarif edilen döndürme matrisi türevini hatırlarsak,

$$ \frac{\mathrm{d} R}{\mathrm{d} t} = \tilde \omega \cdot R $$

Döndürmeyi bir $\omega$ etrafında düşünüyorduk, $\omega$'nin büyüklüğü açısal dönme hızına tekabül ediyordu, ve $\tilde \omega$ eksi-bakışımlı matris idi.

Tüm bunları entegre edici odeint çağrısının kabul edeceği bir formda nasıl kullanırız? Bu çağrı düzleştirilmiş bir liste içinde diferansiyel sonuçların, ve ana değişkenlerin olmasını bekliyor. O zaman $R$'yi kolon bazlı olmak üzere düzleştiririz, ve gerektiği o listeden matris formuna geçeriz, vs.

from scipy.integrate import odeint
from stl import mesh

def skew(a):
   return np.array([[0,-a[2],a[1]],[a[2],0,-a[0]],[-a[1],a[0],0]])

your_mesh = mesh.Mesh.from_file('torus.stl')
prop = your_mesh.get_mass_properties()
R0 = np.eye(3,3)
omega = np.array([1.0,1.0,1.0])
#omega = np.array([0.0,1.0,0.0])
skew_omega = skew(omega)

def dRdt(u,t):   
   R1x,R1y,R1z,R2x,R2y,R2z,R3x,R3y,R3z = u
   R = np.array([R1x,R1y,R1z,R2x,R2y,R2z,R3x,R3y,R3z])
   R = R.reshape((3,3)).T
   res = np.dot(skew_omega, R)
   return list(res.T.flatten())

LIM = 5
STEPS = 20
t=np.linspace(0.0, 3.0, STEPS)
R0 = np.eye(3,3)
u0 = R0.flatten()
u1=odeint(dRdt,list(u0),t)

Üstte görülen mesela R1x $R$ matrisinin 1'inci kolonunun $x$ değişkeni anlamında.

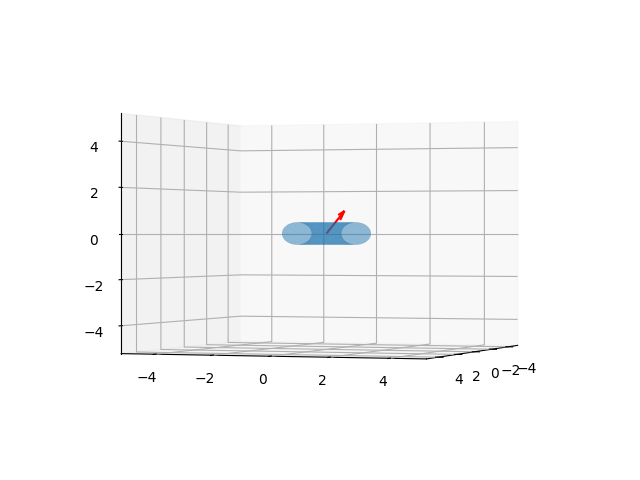
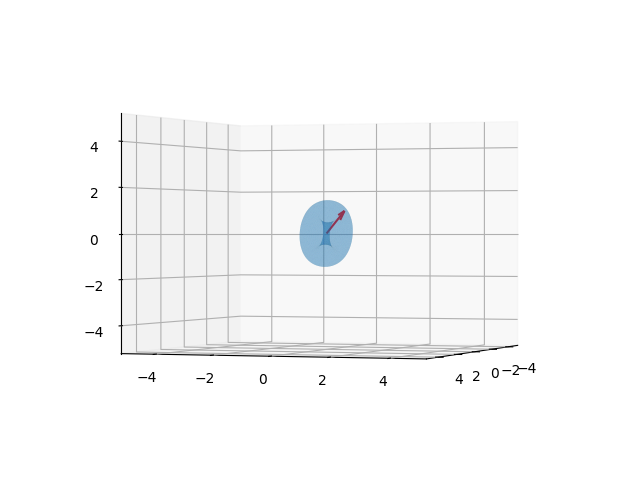
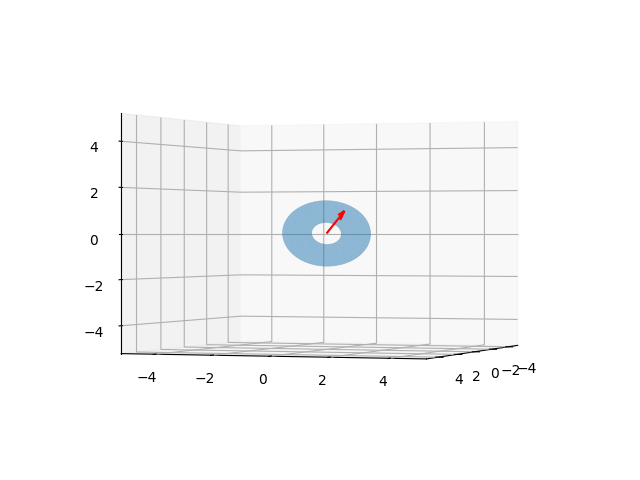
Simülasyonda simit şeklinin baktığı yön $R$ içinde, ve grafik amaçlı olarak her seferinde simit şeklini sıfırdan yükleyip son $R$'ye ilerletiyoruz, ve her adımda bu grafiği basıyoruz. Simülasyonu hesapladık, tüm sonuç u1 içinde, görüntüden bazı seçilmiş kareler altta görülebilir,

import matplotlib.pyplot as plt
from mpl_toolkits import mplot3d

def plot_vector(fig, orig, v, color='blue'):
   ax = fig.gca(projection='3d')
   orig = np.array(orig); v=np.array(v)
   ax.quiver(orig[0], orig[1], orig[2], v[0], v[1], v[2],color=color)
   ax = fig.gca(projection='3d')  
   return fig

for i in range(STEPS):
    fig = plt.figure()
    axes = mplot3d.Axes3D(fig)
    your_mesh = mesh.Mesh.from_file('torus.stl')
    R = u1[i].reshape((3,3)).T
    your_mesh.rotate_using_matrix(R)
    scale = your_mesh.points.flatten()
    axes.add_collection3d(mplot3d.art3d.Poly3DCollection(your_mesh.vectors,alpha=0.3))
    plot_vector(fig, [0,0,0], omega, color='red')
    axes.auto_scale_xyz(scale, scale, scale)
    axes.set_xlim(-LIM,LIM);axes.set_ylim(-LIM,LIM);axes.set_zlim(-LIM,LIM)
    axes.view_init(azim=20,elev=0)
    plt.savefig('/tmp/rotate_%02d.png' % i)  


! convert -delay 20 -loop 0 /tmp/rotate*.png /tmp/rotate1.gif

Animasyon sonucu [4]'te.

Torus şekli hakkında bazı istatistikler alttadır.

from stl import mesh

your_mesh = mesh.Mesh.from_file('torus.stl')

prop = your_mesh.get_mass_properties()
print ('hacim',np.round(prop[0],3))
print ('yercekim merkezi (COG)',np.round(prop[1],3))
print ('COG noktasinda atalet matrisi')
print (np.round(prop[2],3))

hacim 4.918
yercekim merkezi (COG) [-0.  0. -0.]
COG noktasinda atalet matrisi
[[ 3.223 -0.     0.   ]
 [-0.     3.223  0.   ]
 [ 0.     0.     5.832]]

COG sıfır noktasında olması, ayrıca atalet matrisinin köşegen olması mantıklı çünkü simit şekli simetrik.

İttirme Animasyonu

Bu animasyon için katı gövdeye bir noktada bir kuvvet uyguluyacağız. O noktayı seçmek için STL formatında olan üçgenlerden birini kullanabiliriz, çünkü bu üçgenlerin gövdenin yüzeyinde bir yerlerde olduğunu biliyoruz, Torus STL şekli bu üçgenlerin herbirine dik olan normal vektörü STL formatında zaten, o üçgenlerden birinin normal vektörünü ters çevirirsek, o noktaya o yönde bir kuvvet uyguladığımızı hayal edebililriz, ve simülasyonun geri kalanını bu noktadan devam ettiririz.

import matplotlib.pyplot as plt
from mpl_toolkits import mplot3d

fig = plt.figure()
axes = mplot3d.Axes3D(fig)

SCALE = 4
LIM = 5

scale = your_mesh.points.flatten()
axes.add_collection3d(mplot3d.art3d.Poly3DCollection(your_mesh.vectors,alpha=0.3))
axes.auto_scale_xyz(scale, scale, scale)

def plot_vector(fig, orig, v, color='blue'):
   ax = fig.gca(projection='3d')
   orig = np.array(orig); v=np.array(v)
   ax.quiver(orig[0], orig[1], orig[2], v[0], v[1], v[2],color=color)
   ax = fig.gca(projection='3d')  
   return fig

axes.set_xlim(-LIM,LIM);axes.set_ylim(-LIM,LIM);axes.set_zlim(-LIM,LIM)

tidx = 2000
o = np.mean(your_mesh.vectors[tidx],axis=0)
axes.plot (o[0],o[1],o[2],'gd')
n = your_mesh.get_unit_normals()[tidx]
plot_vector(fig, o, n*SCALE)
plot_vector(fig, o, -n*SCALE, color='red')
axes.view_init(azim=84,elev=28)

plt.savefig('phy_005_basics_04_05.png')

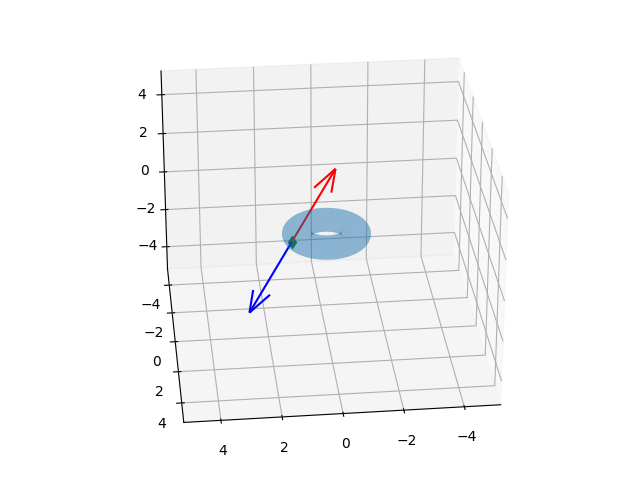
Kuvveti kırmızı vektörle gösterilen yönde uygulayabiliriz.

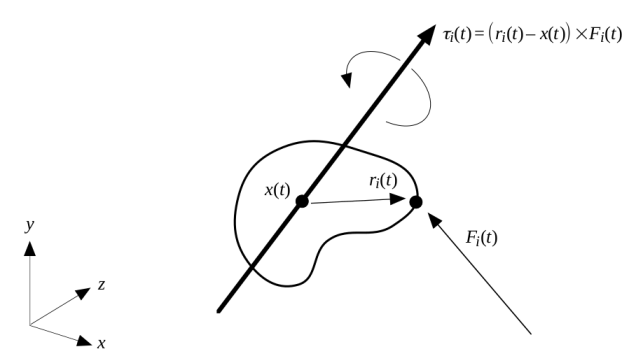
Şimdi "sıfırıncı anda" yani ilk başlangıçta uygulanan kuvvetleri, lineer, açısal, hesaplamak lazım. Noktayı üstte seçtik, sonu o noktada başlangıcı nesne ağırlık merkezinde olan bir vektör ile kuvvet vektörü arasında çapraz çarpım yapıyoruz, bu bize torku veriyor.

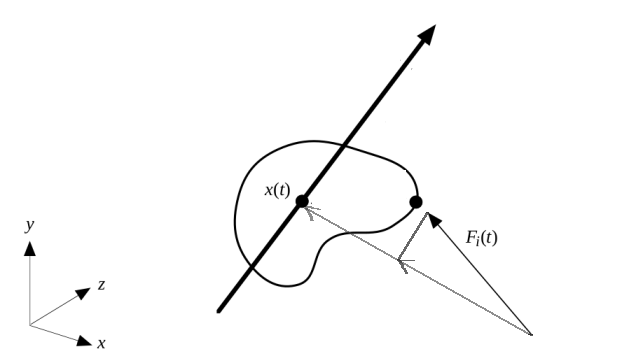
Benzer şekilde sonu nesne merkezinde başı o noktada olan bir vektör daha var, lineer kuvvet bu doğrultuda uygulanacak, o vektör üzerine iki üstte görülen kırmızı vektörü yansıtıyoruz, bu da lineer kuvvet oluyor. Bir üstteki resim üzerinde gösterirsek,

Daha önce söylediğimiz gibi her iki kuvvet de ilk anda lineer ve açısal momentumu ekileyen faktörler, sonraki adımlarda etkileri yok.

Ayrıca entegrasyon için kendi pişirdiğimiz kodları kullanacağız, odeint işleri zorlaştırabilir çünkü zamana bağlı bazı farklı kodlamalar var, ayrıca $I^{-1}$ her adımda sürekli değişiyor, yani bir konum güncellemesi var, bu tür kodlamalar kapalı bir kutu isteyen odeint ile daha zor olabilir. Bunlar problem değil, [5]'te paket kullanmadan hesaplanan bir kodlama şeklini görmüştük.

import numpy as np
from stl import mesh
import numpy.linalg as lin

your_mesh = mesh.Mesh.from_file('torus.stl')   
prop = your_mesh.get_mass_properties()
cog = np.round(prop[1],3) # baslangic aninda obje COG
Ibody = np.round(prop[2],3)
Ibodyinv = lin.inv(Ibody)
dt = 0.1
x = np.zeros((1,3))
R = np.eye(3,3)
L = np.zeros((1,3))
v = np.zeros((1,3))
F = np.zeros((3,1))
M = 1
P = M*v

def skew(a):
   return np.array([[0,-a[2],a[1]],[a[2],0,-a[0]],[-a[1],a[0],0]])

tidx = 2000
apply_at = np.mean(your_mesh.vectors[tidx],axis=0) - cog
f_at = -1 * 5 * your_mesh.get_unit_normals()[tidx]
tau0 = np.cross(apply_at, f_at).reshape(1,3) * 10.0
flindir = cog-apply_at
flin0 = np.dot(f_at,flindir)*(flindir/np.abs(lin.norm(flindir)))

res = []
for i in range(30):
   xold,Rold,Pold,Lold = x.copy(),R.copy(),P.copy(),L.copy()

   Iinv = np.dot(np.dot(Rold, Ibodyinv), Rold.T)
   omega = np.dot(Iinv, Lold.T).T
   omega = omega.reshape(3)
   skew_omega = skew(omega)
   R = Rold + np.dot(skew_omega, Rold) * dt

   v = Pold / M
   x = x + v*dt
   P = Pold
   if i==0: # baslangic ani
      L = Lold + tau0*dt
      P = Pold + (flin0*dt)
   else:      
      L = Lold # sonraki adimlarda degisim yok
      P = Pold # momentum ayni kaliyor
   res.append([x,R,P,L])

Hesaplar yapıldı, şimdi grafikleme,

import matplotlib.pyplot as plt
from mpl_toolkits import mplot3d

LIM = 5
SCALE = 4

def plot_vector(fig, orig, v, color='blue'):
   ax = fig.gca(projection='3d')
   orig = np.array(orig); v=np.array(v)
   ax.quiver(orig[0], orig[1], orig[2], v[0], v[1], v[2],color=color)
   ax = fig.gca(projection='3d')  
   return fig

for i, [x,R,P,L] in enumerate(res):
   fig = plt.figure()
   axes = mplot3d.Axes3D(fig)
   your_mesh = mesh.Mesh.from_file('torus.stl')
   # t-0 aninda uygulanan kuvvet yonunu goster
   o = np.mean(your_mesh.vectors[tidx],axis=0)
   n = your_mesh.get_unit_normals()[tidx]
   plot_vector(fig, o, -n*SCALE, color='red')

   your_mesh.rotate_using_matrix(R)
   your_mesh.translate(x.reshape(3))
   scale = your_mesh.points.flatten()
   axes.add_collection3d(mplot3d.art3d.Poly3DCollection(your_mesh.vectors,alpha=0.3))
   axes.auto_scale_xyz(scale, scale, scale)
   axes.set_xlim(-LIM,LIM);axes.set_ylim(-LIM,LIM);axes.set_zlim(-LIM,LIM)

   az = 80-(i*2) # kamera dondurmek icin
   axes.view_init(azim=az,elev=28)
   plt.savefig('/tmp/rotate_%02d.png' % i)
   plt.close('all')    


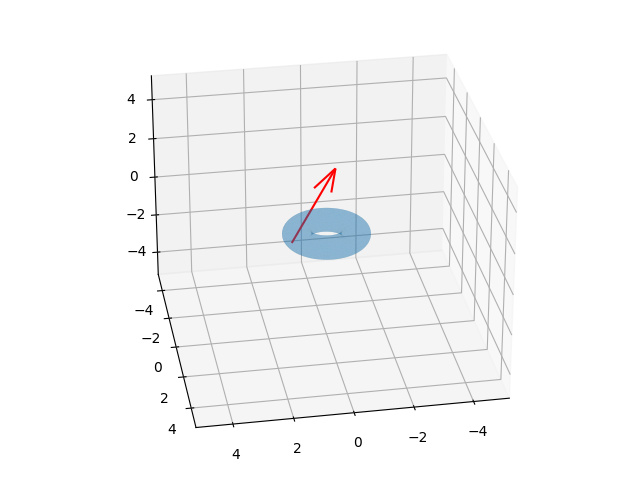
! convert -delay 20 -loop 0 /tmp/rotate*.png /tmp/rotate2.gif

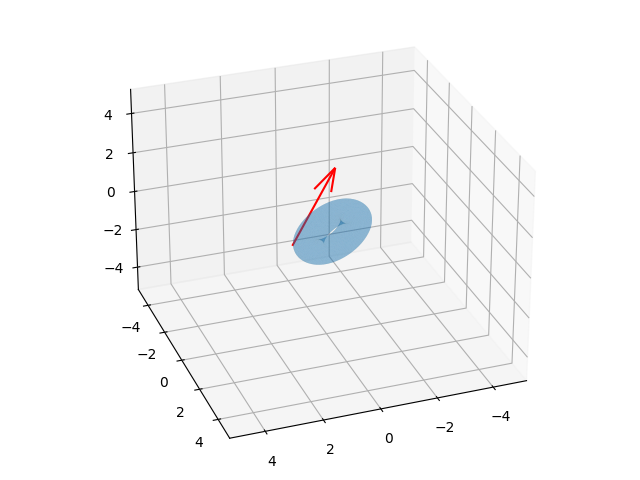
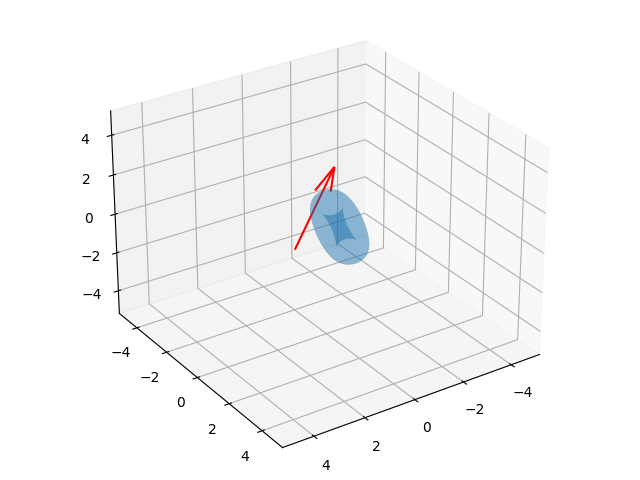
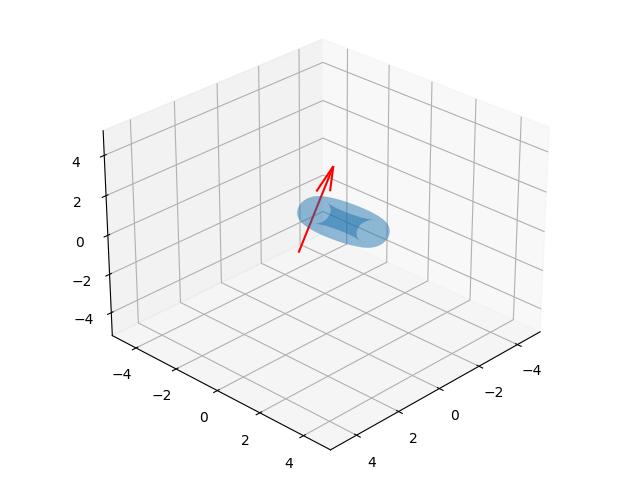
Animasyon sonucu [6]'da görülebilir. Hareket mantıklı gözüküyor, unutmayalım grafikleme açısından kolay olduğu için öyle çizildi fakat aslında hesaplara göre vektörün ucu kuvvet uygulanan noktada, ve uygulanan kuvvet sonrası şekil dönmeye başlayarak ve yukarı doğru uçarak devam ediyor (kuvvet alttan yukarı doğru). Simülasyon ortamı boşluk ortamı, uzay gibi yerçekimsiz bir yer, tek kuvvet ilk başta şekle uygulanan kuvvet, ardından momentum muhafazası ile hareket devam ediyor.

Kaynaklar

[1] Bayramlı, 3D Baskıya Hazır CAD Tasarımlarına Erişmek, Numpy-STL, https://burakbayramli.github.io/dersblog/sk/2020/08/numpy-stl.html

[2] Witkin, Physically Based Modeling

[3] Bayramlı, Animasyon 1, https://drive.google.com/uc?export=view&id=17qlJvaucB6_l0eLUfcevu84qNXQocGHO

[4] Bayramlı, Fizik, Temel Fizik 4, Katı Gövde

[5] Bayramlı, Fizik, Simulasyon

[6] Bayramlı, Animasyon 2, https://drive.google.com/uc?export=view&id=1ZvONRASb4By5zKnuDs6unAVwj0PA8_HK


Yukarı