Ders 2.3

Her hesapsal yöntemin doğruluğu ve stabilitesini bilmek isteriz. En basit başlangıç değer problemi (initial value problem -IVP-) ile başlayalım,

$$ \frac{\partial u}{\partial t} = c \frac{\partial u}{\partial x} \qquad (1) $$

Buna tek yön dalga denklemi diyebiliriz, iki yönlü dalga denklemi için üstteki formülde ikinci türevlerin olması gerekirdi, o tür denklemde dalgalar iki yöne de giderdi. Üstteki tek yöne dalga gönderiyor, basit, temiz bir denklem, birinci derece, hız bağlamında sabit katsayılı. Başlangıç değer problemi için başlangıç değeri $u(x,0)$ ile verilmiş olsun, ve benim ilgilendiğim $u(x,t)$ çözümü.

Bu çözümü bulmak zor olmaz, mesela ilk aklıma gelen pür üsteller, $e^{ikx}$. Bu çözümün bir özelliği sabit katsayısı var, sınırı yok, o zaman çözüm $e^{ikx}$'in bir katı olacak, bu demektir ki değişken ayırma tekniğini uygulayabilirim, ve $u = G(x,t) e^{ikx}$ şeklinde bir çözüm bekleyebilirim. Nasıl değişkenler ayrıldı görüyoruz, $G$ içinde $x$, $t$'den ayrıldı, ve frekans $k$ büyüme faktörü $G$'yi tanımlıyor.

Çözümü bulmak için içinde $G$'yi içeren $u$ formülünü ana türevsel denklem (1)'e sokarım, ve $t$'li çözümü elde ederim, çünkü $e^{ikx}$ iptal olacak. Formüle sokayım,

$$ \frac{\mathrm{d} G}{\mathrm{d} t} e^{ikx} = ikc G e^{ikx} $$

Ustelli kismi iptal ederim, o terimler hic sifir olmazlar nasilsa,

$$ \frac{\mathrm{d} G}{\mathrm{d} t} \cancel{e^{ikx}} = ikc G \cancel{e^{ikx}} $$

Böylece $G$ için basit bir denkleme erişiyorum,

$$ \frac{\mathrm{d} G}{\mathrm{d} t} = ikc G $$

Sonuç sabit bir katsayıya dayaniyor, $ick$ katsayısına. Nihai denklemin bir basit diferansiyel denklem olduğunu da farkediyoruz, o zaman çözüm yine bir üstel, $G = e^{ikc t}$. Bu $G$'yi $u$ çözümü içine koyunca,

$$ u = G(x,t) e^{ikx} $$

$$ u = e^{ikc t} e^{ikx} = e^{ik(x + ct)} $$

Çözüm bu işte. Değişkenleri ayırdık, büyüme faktörüne baktık, bir üsteli denedik, farklılık (difference) metotları için de aynısını yapacağız. Von Neumann'ın dahice fikri buydu, üstelleri takip et. Her frekansa bak, ve $e^{ikx}$'in katlarına neler olduğuna bak.

İlginç bir şey, tüm frekanslar $x+ct$ kombinasyonunu ortaya çıkarıyor. Fourier'in de söylediği bu değil miydi? $e^{ikx}$ kombinasyonlarını alın, onların çözümü $e^{ik(x + ct)}$'lerin kombinasyonu olacak. Yani $x$'ler $x+ct$ oluyor bir bakıma. O zaman çözüm

$$ u(x,t) = u(x+ct, 0) $$

Bu her $u$ için.

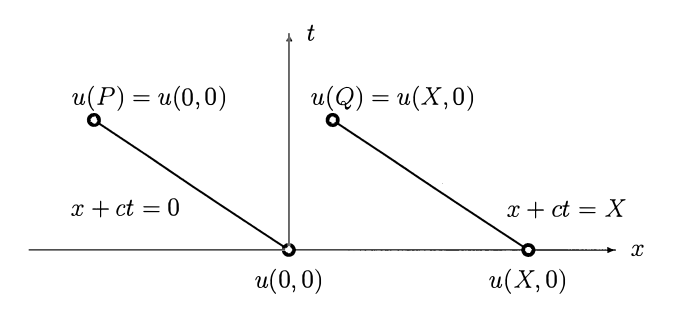
Bu çözümün ne olduğunu sezgisel olarak rahatça anlayabiliriz tabii, bu tek yöne giden bir dalga. Cebirde açıkca görülüyor. $x,t$ düzleminde bir resim çizince daha da iyi görülebilir. Bu resmi anlamak önemli çünkü farklılık yöntemi ile üstteki denklemi çözmeye uğraşıyoruz.

Şimdi $u$'nun $(0,0)$ noktasındaki değerini düşünelim. Zaman geçtikten sonra $x+ct$ çizgisindeki herhangi bir yerde, $P$'de olduğumuzu düşünelim, orada çözüm hep aynı. Başlangıçtaki değer ne ise o çizgi (üstteki grafikte solda görülen) üzerinde seyahat ediyor, $u$ değeri $(0,0)$'da ne $P$'de de o.

Üstte sağdaki çizgi aynı şekilde, orada da $X$ ile işaretli bir sabit değerde başlayan değer çizgi üzerinde yukarı taşınacak, $Q$'da aynı $u$ değeri olacak. [Dikkat, $x$ eksenindeki $X$ değeri $x+ct = X$ çizgisiyle temsil edilir denmiyor, $x$ eksenindeki bir değer ile $.. =X$ şeklindeki bir çizginin cebirsel bağlantısı yok, $ax+by+c=0$ denklemindeki sabitler grafiksel kesim noktalarına tekabül etmezler].

Bu çizgilere karakteristik çizgiler (characteristic lines) ismi veriliyor.

Gördüklerimiz dalga denklemlerine has bir özellik, işi denklemlerinde mesela aynı durum görülmüyor. Tek boyuttayız tabii bunu unutmayalım, oldukca basitleşitirilmiş bir ortam bu. Üç boyutta karakteristik köni var. Üç boyutta düşünürsek, mesela bir ses çıkartıyorum, bir kelime telafuz ediyorum, benim sesim bir ses dalgası bir üç boyuttaki dalga denklemini çözer, ya da parmağımı sıklatsam mesela o ses başlangıç noktasından etrafa yayılır, bu yayılma karakteristikler üzerinden olur. Yayılma pek çok yöne doğru muhakkak, tek boyuttaki gibi tek çizgi değil, yüksek boyutlarda resim biraz daha çetrefil hale geliyor, fakat ana fikri tek boyutta çok iyi görebiliyoruz.

Çözümün kendisinin, yani $u$'nun grafiğini de göstermek faydalı olabilir. Diyelim ki başlangıçta duvar gibi duran, bir su kütlesi var, kabaca onu bir adım (step) fonksiyonu ile gösterebiliriz, $x=0$ solunda 1 değerinde sağında 0 değerinde. Bu IVP'ler için tipik bir başlangıç stili sayılabilir.

Bu grafikte çözümü nasıl gösterirdik? Yani $u(x,t)$ çözümü, grafiği nedir? Grafik üstteki şeklin sola doğru hareket etmesiir. Dalga sola doğru $c$ hızıyla gidiyor yani ($c$ pozitif ise). Dalga denkleminin her çözümü bu şekilde davranır, bu örnekte bir su duvarı düşündük, ve o duvar sola doğru hareket etti. Önemli nokta şu kütlesi bu hareket sırasında şekil değiştirmeyecektir, saçılma (dışpersion) kelimesini kullanmak belki de doğru, o yoktür yani. Hareket esnasında her frekans (eğer o su duvarını, dalgayı, bir kaç pür üstelin toplamı olarak düşünürsem, ki bu tür bir Fourier'den biliyoruz ki mümkündür) aynı hızda hareket ediyor, bu sebeple tüm dalga da o hızda hareket etmiş oluyor.

[gerisi atlandı]