Ders 1-18

Sonlu Öğeler, 2. Bölüm

Üzerinden geçelim, sistem zayıf form ile ise başlar. Önceki dersin sonunda Galerkin fikrini tanıştırdık, sürekli diferansiyel denklem yerine onu ayrıksal temsil etmeye uğraştık. Galerkin bunun için bazı deneme fonsiyonları kullanır onlara $\phi_1,...,\phi_N$ diyelim, ayrıca test fonksiyonları da vardır (fakat çoğunlukla test fonksiyonları ile deneme, yani $\phi$ ve $v$ fonksiyonları aynı seçilir). Bugün işleyeceğimiz bu fonksiyonların nasıl seçildiği ve hazırlık aşamasını gösterdikten sonra elde edilen $KU = F$ denkleminin nasıl çözüldüğü. $K$ nereden geliyor, $F$ nereden geliyor? $F$ bir şekilde alttaki ikinci denklemin (oktan sonra) sağ tarafından geliyor, $K$ ise sol tarafından.. Detayları şimdi göreceğiz.

$$ - \frac{\mathrm{d}}{\mathrm{d} x} \left( c(x) \frac{\mathrm{d} u}{\mathrm{d} x} \right) = f(x) \to $$

$$ \int_{0}^{1} c \frac{\mathrm{d} u}{\mathrm{d} x} \frac{\mathrm{d} v}{\mathrm{d} x} \mathrm{d} x = \int_{0}^{1} f(x) v(x) \mathrm{d} x \qquad (1) $$

ki eğer $u(1)=0$ ise $v(1) = 0$ (sınır şartı).

Sonlu öğeler metotunun (FEM) temeli $KU = F$. Üstteki denklemde okun sol tarafı diferansiyel denklemimiz, sınır şartları vs ile "güçlü formda", oktan sonrası zayıf form, ki onun da kendi sınır şartları var. Sabit değişkenler güçlü formdan zayıf forma geçiyor, ama serbest değişkenler geçmiyor. $v$'yi $u$'dan olan ufak sapmalar olarak gördüğüm için eğer $u$'yi sabitliyorsam $v$ de sabitleniyor.

Tüm bunları gördük ama hala ayaklarımız yere basmadı; bir çok fikirden bahsettik, ama şimdi daha gerçek dünyaya bağlanacağız. Gerçek dünya demek tabii $\phi$'lerle alakalı, hangi somut fonksiyonları $\phi$ olarak seçeceğiz?

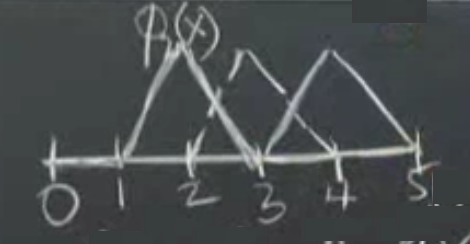
Acaba örnek bir $\phi$ ne olabilir? Mesela $x=2$ noktasında tepe yapan bir parçalı lineer fonksiyon kullanabilirim,

Bu fonksiyona $\phi_2(x)$ diyelim, 1 ila 3 arasında 2 üzerinde tepe yapıyor diğer yerlerde ya lineer eğimi var, ya da değeri sıfır. Her $\phi$ maksimum tepe noktası 1 olarak seçilebilir. Onun sağındaki $\phi_3$ olabilir, benzer bir fonksiyon sadece 3 değeri bazlı tanımlı. Buradaki ana amaç sistemı basit ögeler üzerinde inşa etmek. FEM'in ana fikri budur; $\phi$ için basit fonksiyonlar kullan. Bu basitliğin devamı olarak $\phi$ ve $v$ fonksiyonlarını aynı seç.

Peki sınır noktalarında ne olacak? Üstte serbest-sabit problemi çözeceğim, sol üç nokta serbest, sağ üç nokta sabit (sınır tanımlanmış).

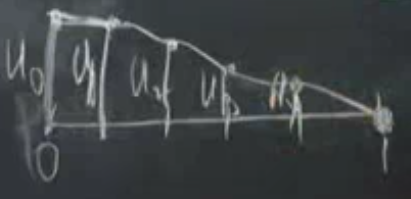
Üstteki resme bakarsak, $x=0$ için bir "yarım şapka" fonksiyonu tanımladım, $\phi_0$ diyelim, ve eğer diğer üçgen fonksiyonlara tam şapka dersek bu da yarım şapka. O noktada $\phi$ ve $v$'lerim kısıtlı değiller. Böylece elimde beş tane deneme fonksiyonu oluyor, $\phi_0$, $\phi_1$, $\phi_2$, $\phi_3$, $\phi_4$.

Amaç nedir? Yaklaşık FEM çözümüm $U(x)$'in üstteki basit şapka fonksiyonlarının bir kombinasyonu olmasını istiyorum.

$$ U(x) = U_0 \phi_0(x) + ... + U_4 \phi_4(x) \qquad (2) $$

$U_0,..,U_4$ değerleri skalar, tek sayı.. onlar ilk başta bilinmeyen "ağırlık" değerleri, $\phi$'leri belli şekilde çarpacaklar ve bu çarpımların toplamı yaklaşık bir $u$ olacak.

Bu kombinasyonlar neye benzerdi acaba? Şöyle olabilirdi,

Başlangıçtaki değer niye $u_0$? Çünkü orada tüm diğer $\phi$ fonksiyonları sıfır seviyesinde, hemen yandaki $\phi_1$ bile orada sıfır ve maksimum $\phi$ değer 1 olduğu için başlangıç değeri $u_0$.

Bu arada Galerkin, ismini taşıyan yöntemi bulurken, aklında erişmeye uğraştığı belli bir çözüm fonksiyonu vardı, ve şapka fonksiyonlarını oraya varmak için seçmişti fakat modern FEM yaklaşımlarında, yazılımlarında bir temel fonksiyonu ilk baştan seçeriz, problem hakkında bir şey bilmesek bile. Şapka fonksiyonları bu fonksiyonlardan biridir.

Sonlu öğeler temel fonksiyonları düğüm noktalarıyla bağlantılıdır, bu bağlamda sonlu farklılıkler (finite differences) metotuna benzer, öğeler düğüm noktalarına oturtuluyor. FEM ile şapka fonksiyonu özelinde her düğüm noktasındaki $u$ değerinin o noktadaki ağırlık değeri ile aynı olmasını zorlamış oluyoruz; mesela 1 düğümündeki değer nedir? $u_1$! Çünkü orada diğer tüm şapka fonksiyonları sıfırdır, sadece $\phi_1$ değeri 1, toplanan tüm terimler yokoluyor geriye sadece $u_1 \phi_1 = u_1$ kalıyor.

FD benzerliği hakkında, $KU=F$'i oluşturduğumuzda onun bir FD denklemine oldukca benzediğini göreceğiz, arada yapısal farklar var tabii, FD ile ayrıksal denklemleri biz tanımlıyoruz, FEM ile sadece baz öğeleri seçiyoruz denklemin ne olduğunu Galerkin yöntemi bize söylüyor.

Şimdi bize lazım olan üstteki resimdeki her nokta için ayrı bir denklem, yani toplam 5 tane denklem. Bu denklemler nereden gelecek? Kritik bir soru.

Bu denklemler zayıf formdan gelecekler. Şunu yapıyorum, (1)'deki $u$ yerine (2)'deki $U$'yu sokuyorum. Ayrıca bir $v$ lazım, daha önce $v(1)=0$ şartı takip edilmek suretiyle herhangi bir $v$ olabilir demiştik, ama şimdi ayrıksal forma geçtik, ben de $\phi_i$ fonksiyonlarını $V_i$ fonksiyonlarım için kullanmaya karar veriyorum. Böylece,

$$ \int_{0}^{1} c(x) \frac{\mathrm{d} U}{\mathrm{d} x} \frac{\mathrm{d} V_i}{\mathrm{d} x} \mathrm{d} x = \int_{0}^{1} f(x) V_i(x) \mathrm{d} x \qquad (3) $$

ki $i=0,1,2,3,4$. Böylece 5 tane denklem elde ediyorum, 5 tane $V$ ile ana formülü "test ediyorum". Yani üstteki denklemi 5 tane $V$ için farklı şekillerle üretmiş oluyorum. İşte 5 x 5 sistemim bu. Neler yaptım şimdiye kadar? Baz fonksiyonlarını seçtik, onları zayıf forma sokuyoruz. $\mathrm{d} U / \mathrm{d} x$ ağırlıklı toplamdan geliyor (dikkat tüm $V$'leri kullanarak), sonra $\mathrm{d} V_i / \mathrm{d} x$ sokuyoruz, ve entegrali hesaplıyoruz. FD durumunda bu hesap yoktu, entegral hesabı yani, FEM ile var, eşitliğin hem sağında hem de solunda. Eşitliğin sağındaki entegral her $V_i$ için bize bir $F_i$ verecek, yani $F$ vektörünün bir satırını. Tabii $K$ matrisi eşitliğin solundan bir şekilde çıkacak, nasıl birazdan göreceğiz.

Örnek

Sağ tarafa bakalım önce, mesela $i=0$ için, $f(x)=1$ olsun (örneğe göre böyle) bu durumda $\int_{0}^{1} 1 \cdot V_0(x) \mathrm{d} x$ entegrali ne olur? Entegral bir alan hesabıdır hatırlarsak, o zaman

$V_0$ üstteki ilk yarım şapka, o üçgenin alanı, eğer $x$ ekseni eşit aralıklarla bölmüşsek ve her aralık $\Delta x$ ise, $(\Delta x \cdot 1) / 2 = \frac{\Delta x}{2}$.

Dikkat 0 ila 1 arası entegral üstteki resimdeki tüm yatay ekseni kapsar, 0,1,2,.. indisleri kafa karıştırmasın. O indisler $x=0$ ile $x=1$ arasını indisliyor. O zaman 0 ile 1 arası entegral tüm $V$'lerin olduğu alan üzerinden alınır, fakat biz her seferinde birini seçtiğimiz için onun alanını hesaplamış oluyoruz çünkü mesela $V_0$ tanımlandığı yer sonrasında sıfır değerinde.

$i=1$ için ne olur? $\int_{0}^{1} 1 \cdot V_1(x) \mathrm{d} x$, üçgen tabanı $2 \Delta x$, çarpı 1, sonuç $\Delta x$. diğer $V$ değerleri benzer şekilde, o zaman $F$ vektör şu şekilde,

$$ F = \left[\begin{array}{c} 1/2 \\ 1 \\ 1 \\ 1 \\ 1 \end{array}\right] $$

$K$ için hazır mıyız? Anahtar bölüm orası.

(3) formülünün tüm sol tarafı $KU$'yu vermeli.. Satır satır gidelim, mesela sıfırıncı denklem hangisi? $i=0$ olduğu zaman, yani $V_0$ kullanılan, zayıf formu $V_0$ ile test ettiğimiz durumdur. Her şeyi açarak yazarsak,

$$ \int_{0}^{1} c(x) \left( U_0 \phi_0' + ... + U_4 \phi_4' \right) \frac{\mathrm{d} V_0}{\mathrm{d} x} \mathrm{d} x = F_0 = \Delta x \cdot \frac{1}{2} $$

Şu ana kadar eldekileri matris formunda yazarsak,

$$ \left[\begin{array}{rrrrr} & & & & \\ & & & & \\ & & & & \\ & & & & \end{array}\right] \left[\begin{array}{r} U_0 \\ U_1 \\ U_2 \\ U_3 \\ U_4 \end{array}\right] = \left[\begin{array}{r} F_0 \\ F_1 \\ F_2 \\ F_3 \\ F_4 \end{array}\right] $$

Boş matrisin ilk satırını $V_0$'yi kullanarak yapacağım entegral hesabından elde edeceğim. Daha kolay başlayalım, ilk satırın sol ilk hücresine ne gelir? $K_{00}$ diyelim, oradaki değer $U_0$'i çarpıyor değil mi ve bir şekilde entegralinin alınması lazım.. Şöyle olabilir mi?

$$ K_{00} = \int_{0}^{1} c(x) \phi_0' V_0' \mathrm{d} x $$

$c(x)$ için şimdilik 1 kabul edelim. Fakat eğer 1 olmasaydı daha çetrefil bir fonksiyon olsaydı? İçinde $c(x)$ olan birçok entegrali üstteki gibi hesaplamak lazım, ve bu hesapların kesin olması gerekmeyebilir, yani bu entegralleri yaklaşık olarak hesaplasak ta yeterli olabilir. Sonuçta diğer her şeyi yaklaşık yapıyoruz değil mi? Belli noktalar üzerinden yaklaşık bir temsil yaratıyoruz vs.. Bu çerçevede eğer üstteki türden entegralleri hesabın tümünü bozmayacak seviyeye yetecek kesinlik3te hesaplayabilirsek, işimizi halletmiş oluruz. $c(x)$ 1 olunca tabii ki kesin çözümü bulacağız ama diğer tür durumlar için aklımızda olsun.

Hesabın kendisine gelelim. $\phi_0'$ nedir? Bu arada $\phi$'leri $V$ ile aynı seçtiğimiz için $\phi_0' = V_0'$ ve her iki türev üstteki resimdeki baştaki yarım üçgenin eğimi. Eğitim dikey artış bolu yatay artış, yatay kısım $\Delta x$, o zaman 1'inci dugume kadar $- 1 / \Delta x$, sonrası sıfır.

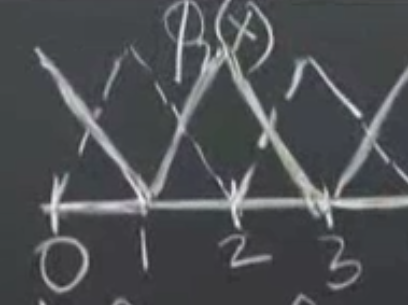
Bu vurgulanması gereken bir noktaya götürüyor, fonksiyonlarımız yerel / lokal. Bu ne demek? Eğer $\phi_1'$ türevini $V_4'$ türeviyle entegre etseydim ($K$ matrisinde 4'uncu satır ile 1'inci kolon değeri yani) ne olacaktı? Sıfır olacaktı. Niye? Çünkü bu fonksiyonlar yerel, 0'inci ve 4'uncu düğümlerden uzakta değerleri sıfır, sıfır olmadıkları yerler çakışmıyor. Şimdi bu dinamiği tüm matris için düşünürsek ne kadar az çakışma yeri olduğunu görebiliriz. Herhangi bir $\phi$ mesela, tabii ki kendisiyle çakışır ve yanindaki komşularla biraz çakışır. Ama daha ilerisiyle örtüşmesi yoktur. Bu bize $K$ için üçlü köşegen bir matris verecek, üç öğeli köşegen bantında değerler olacak, geri kalan her yer sıfır.

$K_{00}$ hesabına dönelim, $c(x)=1$, $\phi_0' = -1/\Delta x$, $V_0'$ aynı değer, ve entegre ettiğimizi unutmayalım, 0 ile 1 arası ama aslında 0 ile $\Delta x$ arası çünkü sadece oraya kadar değerler var, o zaman $K_{00} = 1/\Delta x$ oluyor.

Peki

$$ K_{11} = \int_{0}^{1} c(x) \phi_1' V_1' \mathrm{d} x $$

$\phi_1$ eğimi nedir? Bu şapka fonksiyonu tam, $\Delta x$'e kadar yukarı çıkıyor sonra aşağı ınıyor, o zaman

$$ \phi_1' = V_1' = \left\{ \begin{array}{rc} 1/\Delta x & 0 < x \le \Delta x \\ -1/\Delta x & \Delta x < x \le 2\Delta x \end{array} \right. $$

$\phi_1'$ ve $V_1'$ çarpımı her iki bölüm için $1/\Delta x^2$ verir. Peki $K_{11}$ entegral sonucu ne o zaman? $2 \Delta x$ değil mi? Çünkü bu sefer entegral sınırlarına dikkkat, 0 ile $2\Delta x$ arasında.

$$ K_{11} = \int_{0}^{2\Delta x} c(x) \phi_1' V_1' \mathrm{d} x = 2\Delta x $$

$K_{22}$, $K_{33}$, .. benzer şekilde olacak.

Peki $K_{01}$ ne olur? Yani sıfırıncı satır ve 1'inci kolona bakıyorum. Her iki şapka fonksiyonunu çizersek,

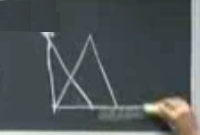
Görüldüğü gibi biri yarım, diğeri tam, ama çakıştıkları yer hocanın gri kalın şeritle gösterdiği bölümden öncesi. Ondan sonrası $\phi_0$ sıfır değerinde orada entegral almaya gerek yok.

Tabii entegre edilen eğimler, $\phi_0'$ $-1/\Delta x$ olacak, $V_1'$ ise pozitif değerli, $1/\Delta x$. Çarpımları $-1/\Delta x^2$ entegre sınırı 0 ile $\Delta x$ arası, entegrasyon sonucu $K_{01} = 1-/\Delta x$. n

Köşegen bir üstü ve bir altı aşağı çapraz inen tüm satırlar için aynı şey geçerli, çünkü hepsi de yanyana olan $\phi$ ve $V$ üzerinden entegral alıyor olacaklar

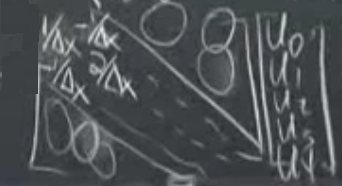
Tüm matrisi doldursak görürdük ki $K$ matrisi simetrik, pozitif kesin olacak. Hatta onun ötesinde biraz basitleştirme sonrası üstteki matris bize bu dersten daha da tanıdık gelebilir. Eğer $1/\Delta x$ dışarı çekilirse bizim $T$ matrisi ortaya çıkıyor,

$$ K = \frac{1}{\Delta x} \left[\begin{array}{rrrrr} 1 & -1 & & \\ -1 & 2 & -1 & & \\ & -1 & 2 & -1 & \\ & & -1 & 2 & -1 \\ & & & 1 & 2 \end{array}\right] $$

Hepsini bir araya koyarsak,

$$ KU = \frac{1}{\Delta x} \left[\begin{array}{rrrrr} 1 & -1 & & \\ -1 & 2 & -1 & & \\ & -1 & 2 & -1 & \\ & & -1 & 2 & -1 \\ & & & 1 & 2 \end{array}\right] \left[\begin{array}{r} U_0 \\ U_1 \\ U_2 \\ U_3 \\ U_4 \end{array}\right] = \Delta x \left[\begin{array}{r} 1/2 \\ 1 \\ 1 \\ 1 \\ 1 \end{array}\right] = F $$

Basit örneğimiz için FEM sistemi $KU = F$ işte bu.

Gerçi üstteki denklem sonlu farklılıklara (FD) benzer bir sistem ortaya çıkarttı, derse o sebeple 'bu iki yaklaşımın farkı nerede?' sorusuyla başlamıştım. Fakat dikkatli bakarsak bu çok basit problemde bile ufak bir fark var, üstteki vektörde 1/2 var mesela, FD sistemine bu yok. Ama tabii $F$ 1 değilse ya da $c$ 1 değilse daha fazla farklar ortaya çıkacaktır, $c$ 1 değilse bir sürü çetrefil entegral ortaya çıkar, onları yaklaşık şekilde temsil etmeye uğraşırım muhakkak.

Ya $F$ için pür 1 değil mesela nokta yük (point load) $\delta (x-\frac{1}{5})$ olsaydı elimizde? Şimdi entegrallere geri dönmem gerekiyor değil mi? (3) denklemindeki eşitliğin sağ tarafındaki entegralden bahsediyorum. Şimdi o entegralde 1 yerine noktasal yük var

$$ = \int_{0}^{1} \delta (x-1/5) V_i \mathrm{d} x $$

diye gidiyor, yani $\delta (x-1/5)$ fonksiyonunu her şapka fonksiyonuna karşı entegre etmem gerekiyor. Ne elde ederim? Delta fonksiyonu 1/5 noktasındaki değeri çekip çıkartır, çünkü o noktada zıplama yapıyor, orada entegrali, alanı 1, o zaman 1/5 üzerindeki $V_i$ değerini seçecektir. O da $i=1$ olur, demek ki iki üstteki eşitliğin sağ tarafı suna benzer,

$$ = \Delta x \left[\begin{array}{r} 0 \\ 1 \\ 0 \\ 0 \\ 0 \end{array}\right] = F $$

Gerçi bu da FD'nin üreteceği sonuca biraz benzer.

Ya nokta yükü düğüm üzerinde değil iki düğüm arasına gelecek şekilde seçseydim? Mesela 3/10 noktasında? O zaman entegraller bana

$$ = \Delta x \left[\begin{array}{r} 0 \\ 1/2 \\ 1/2 \\ 0 \\ 0 \end{array}\right] = F $$

verirdi değil mi? Görüyoruz, FEM nasıl otomatik olarak akılcı olan şeyi yaptı.. Noktasal yükün etkisini iki vektör hücresine yaydı. Otomatik olarak $c(x)$'i, $f(x)$'i esnek şekilde probleme dahil ediyor, serbest sınırı idare ediyor.. FD bunu yapamazdı, çünkü FD katı olarak düğümler üzerinde tanımlıdır.

Alttaki Eski Bir Ders Video'sundan Alınmıştır

Sonlu Öğeler Metodu (Finite Elements Method)

Bu metot differansiyel, kısmi differansiyel denklemleri (partial differential equations) yaklaşıksal olarak modelleme ve çözmenin yöntemleridir.

Formül: Başlangıç denklemi

$$ \frac{-d}{\mathrm{d} x} \bigg( c(x) \ \frac{\mathrm{d} u}{\mathrm{d} x} \bigg) = f(x) $$

İki tarafı da $v(x)$ ile çarpıyoruz ve 0 to 1 sınırlarıyla entegralini alıyoruz.

$$ \int_0^1 \frac{-d}{\mathrm{d} x} \bigg( c(x) \frac{\mathrm{d} u}{\mathrm{d} x} \bigg) v(x)\mathrm{d} x = \int_0^1 f(x)v(x) \mathrm{d} x $$

Parçalı entegral (integration by parts) formülü şöyledir:

$$ \int y \mathrm{d} z = y z - \int z \mathrm{d} y $$

Ana formülün bölümlerini, parçalı entegrale göre bölüştürürsek:

$$ dz = \frac{-d}{dx} \bigg( c(x) \ \frac{du}{dx} \bigg) dx $$

$$ z = - c(x) \ \frac{du}{dx} $$

$$ y = v(x) $$

$$ dy = \frac{dv}{dx}dx $$

Yukarıda $dz$ içinde $dx$ ve $\frac{1}{dx}$ birbirini iptal eder. Parçalı entegral formülünün sağ tarafına göre yerlerine koyarsak:

$$ \int_0^1 v(x)\mathrm{d} x \frac{-d}{\mathrm{d} x} \bigg( c(x) \frac{\mathrm{d} u}{\mathrm{d} x} \bigg) = - \bigg[ v(x) c(x) \frac{\mathrm{d} u}{\mathrm{d} x} \bigg]_{x=0}^{x=1} \int_0^1 c(x) \frac{\mathrm{d} u}{\mathrm{d} x} \frac{\mathrm{d} v}{\mathrm{d} x} \mathrm{d} x $$

Üstteki parçalı entegral açılımında sol taraf entegrale sınır değerleri aldığında, sağ taraftaki $yz$ sonucunun aynı sınır değerlerine tabi olduğuna dikkat edelim.

Differansiyel denklemde sınır koşulları $x=1$ durumunda $c(1)u'(1)=0$, ve $x=0$ durumunda $v(0)=0$ olarak biliniyor. O zaman üstteki denklemin sol tarafında $x=0$ ve $x=1$ koşulları için tanımlı bölüm $0 - 0 = 0$ olacaktır ve denklemden atılabilir. Geriye kalanlar

$$ \int_0^1 c(x) \frac{\mathrm{d} u}{\mathrm{d} x} \frac{\mathrm{d} v}{\mathrm{d} x} \mathrm{d} x = \int_0^1 f(x)v(x) \mathrm{d} x $$

Bu fonksiyonu Galerkin adlı bir matematikçi bulmuş, "zayıf form (weak form)" olarak adlandırılıyor.

Şimdi diyelim ki n tane test fonksiyonu seçtik $\phi_1(x),..,\phi(n)$ ve bu fonksiyonların $U_j$ sayıları ile çarpımının toplamını, yani bir tür kombinasyonunu $u(x)$ yerine kullanmaya karar verdik.

$$ U(x) = U_1 \phi_1+ ... + U_n\phi_n $$

O zaman

$$ U'(x) = U_1 \phi_1'+ ... + U_n\phi_n' $$

$$ = \sum_1^n U_j \frac{d\phi_j}{dx} $$

Şimdi $du / dx$ yerine $U'(x)$ koyarsak

$$ \int_0^1 c(x) \bigg( \sum_1^n U_j \frac{\mathrm{d}\phi_j}{\mathrm{d} x}\bigg) \frac{\mathrm{d} V_i}{\mathrm{d} x}\mathrm{d} x = \int_0^1 f(x)V_i(x)\mathrm{d} x $$

Dikkat edelim, $v(x)$ yerine $V_i(x)$ kullandık. Üstteki formül her i için yeni bir formül "üretecek". Niye $V_i$? Zayıf formdaki $v(x)$ formülünü de zaten biz uydurmuştuk, yani $v(x)$ biz ne istersek o olur. O zaman bu fonksiyonu n tane formül üretmek için bir numara olarak kullanıyoruz, n tane formül olunca matrisin n x n elemanını doldurabileceğiz ve çözüme erişebileceğiz. Ek not, çoğunlukla $V_i(x)$ için $\phi_i$ sembolü kullanılıyor.

Ayrıca formüldeki $U_j$ kısmını cekip çıkartırsak ve bir vektör içine koyarsak, geri kalanlar bir $K_{ij}$ matrisi içinde tutulabilir.

$$ K_{ij} = \int_0^1 c(x) \frac{\mathrm{d}\phi_j}{\mathrm{d} x} \frac{\mathrm{d} V_i}{\mathrm{d} x} \mathrm{d} x $$

Sağ taraf aynı şekilde i tane formül üretir

$$ F_i = \int_0^1 f(x)V_i(x) \mathrm{d} x $$

Final formül matrix formunda basit bir şekilde temsil edilebilecektir.

$$ KU = F $$

Örnek

Örnek olarak $-u" = 1$ denklemini çözelim. Not: Differansiyel denklemlerde sonuç bulmak demek bir "fonksiyon" bulmak demektir. Normal cebirsel denklemlerde sonuç bulmak değişkenlerin "sayısal" değerini bulmak demektir. Birazdan bulacağımız sonuç $u(x)$ "fonksiyonu" olacak.

Eğer denklem $-u"=1$ ise o zaman bu formülü ana forma uygun hale getirmek için $c(x) = 1$ olarak almamız gerekir. $-u"=1$ denkleminde eşitliğin sağ tarafı 1 olduğuna göre $f(x) = 1$ demektir.

Artık $\phi$ fonksiyonlarını seçme zamanı geldi. Bu fonksiyonların "toplamı" hedeflediğimiz fonksiyonu yaklaşıksal (approximate) olarak temsil edecek. Örnek olarak seçebileceğimiz bir fonksiyon "şapka fonksiyonu (hat function)" olarak bilinen üçgen fonksiyonlar olabilir. Alttaki figürde bu fonksiyonları görüyoruz.

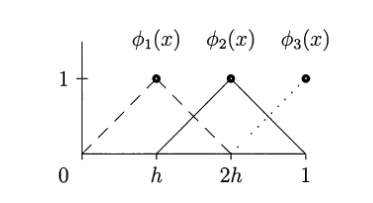
Bu figürde x ekseninin h büyüklüğündeki parçalara bölündüğünü görüyoruz.

Entegralleri hesaplayalım

$$ F_1 = \int_0^1 V_1(x) \mathrm{d} x $$

Daha önce $V_1$ ve $\phi_1$'i aynı kabul ettiğimizi belirtmiştik.

Yukarıdaki entegralin aslında bir alan hesabı yaptığını görüyoruz. Sınırlar $0$ ve $1$ arasında, ama $2h$ ötesinde zaten $\phi_1$ fonksiyonu yok. $\phi_1$'in alanı nedir? Alan üçgenin alanı: Taban çarpı yükseklik bölü 2: $2h$, yüksekliği $1$, o zaman alan $(2h \times 1) / 2 = 1/3$

Benzer mantıkla bakarsak, $F_2$ ile $F_1$ aynı, yani $1/3$. $F_3$ ise onların yarısı, yani $1/6$.

$K_{ij}$ nasıl hesaplanacak? $c(x) = 1$ olduğu için formülden çıkarılabilir ve $V_1$ ve $\phi_1$'in aynı olduğuna söyledik:

$$ K_{ij} = \int_0^1 c(x) \frac{\mathrm{d}\phi_j}{\mathrm{d} x} \frac{\mathrm{d} V_i}{\mathrm{d} x} \mathrm{d} x $$

$$ K_{11} = \int_0^1 \bigg( \frac{\mathrm{d} V_1}{\mathrm{d} x} \bigg) ^2 \mathrm{d} x $$

$dV_1/dx$ nedir? Birinci şapka fonksiyonunun türevidir. Bu türeve bakarsak, $0$ ve $h$ arasında artı eğim (slope) $1/h$, $h$ ve $2h$ arasında eksi eğim $-1/h$ oluyor. Ama kare aldığımız için sonuç aynı, $1/h^2$. O zaman h = 1/3 olduğuna göre $1/(1/3)^2$, yani $dV_1/dx = 9$.

$$ K_{11} = \int_0^{2/3} 9 \mathrm{d} x = 9x \bigg|_0^{2/3} = (9)(2/3) - 0 = 6 $$

$K_{22}$ şeklen aynı fonksiyon parçasını temel aldığı için aynı değere sahip: 6. $K_{33}$ onların yarısı, eşittir 3.

$K_{12}$ farklı eğimlerin çarpımı anlamına gelir, yani $V_1'$ ile $V_2'$ çarpımı olur. Bu iki fonksiyona bakalım, 0 ile h arasında $V_2$ yok, eğim 0. İkisinin de sıfır olmadığı, çarpımda kullanılabilecek bir eğiminin olduğu tek aralık h ve 2h arası. Burada $V_1' = -3, V_2 = 3$.

$$ K_{12} = \int_{1/3}^{2/3} (3)(-3) \mathrm{d} x = -9x \bigg|_{1/3}^{2/3} = -6 - (-3) = -3 $$

Aynı şekilde $K_{23} = -3$. Ama $K_{13} = 0$ çünkü hiç çakışma yok.

Matrisi doldurursak,

$$ KU = F $$

$$ \left[\begin{array}{ccc} 6 & -3 & 0 \\ -3 & 6 & -3 \\ 0 & -3 & 3
\end{array}\right] \left[\begin{array}{c} U_1 \\ U_2 \\ U_3 \end{array}\right] = \left[\begin{array}{c} 1/3 \\ 1/3 \\ 1/6 \end{array}\right] $$

Python kodu

K = [[6., -3., 0],
     [-3., 6., -3.],
     [0., -3., 3.]]

f = [1./3., 1./3., 1./6.]

print np.linalg.solve(K,f)

[ 0.27777778  0.44444444  0.5       ]

print 5./18., 4./9., 1./2.

0.277777777778 0.444444444444 0.5

Rapor edilen değerler bu denklemin bilinen çözümü $u(x) = x - \frac{1}{2}x^2$ ile 0, h, 2h noktalarında (mesh points) birebir uyum gösterdiğini görüyoruz. Yani yaklaşıksal olarak differansiyel denklemi çözmeyi başardık.

Kaynaklar

[1] Strang, G., Computational Science and Engineering