Ders 1-15

Makaskirişler (Truss)

Bir makaşkiriş esneyebilen çubuklardan (bar) oluşur, bu çubuklar birbirine bağlantı pimleri (pin joint) ile bağlıdır. Bağlantı pimi derken şunu kastediyorum, çubukları esnetmek özellikle uzunluğu yönünde kuvvet gerektirir, ama pim etrafında çubukları döndürmek efor gerektirmez.

Not: Burada önemli bir nokta dış kuvvetin sadece bağlantı noktalarına uygulanması, ve kuvvetlerin tüm yapı içinde sadece eksenel (axial) yönde hissedilmesi [3, sf. 5].. Makaskirişlerde moment yoktur, sadece eksenel kuvvet vardır. Bu durum bazı analizleri muhakkak kolaylaştırır. Çubukları birbirine bağlayarak dayanikli yapı oluşturmanın farklı yolları var, çerçeve (frame) bunlardan bir diğeri, bu yapıda kuvvet hem bağlantıya hem de kirişlerin herhangi noktasına uygulanabilir.

Mesela resimdeki 3 no'lu çubuğu sağa ve sola esnetmek zor, ama o çubuğu 3 no'lu pim etrafında döndürmek kolay.

Bu derste iki boyutlu makaşkirişler incelenecek, daha önce iki boyutlu yay-kütle sistemini incelediğimiz gibi; muhakkak üç boyutlu makaşkiriş sistemleri de var ama iki boyut üzerinde ana başlıkları daha rahat olarak inceleyebiliriz.

Üstte görülen örnekte 5 tane çubuk 3 tane düğüm (nod, pim noktası) görüyorum. Peki bilinmeyenler ne? Yani daha önceki yay-kütle problemindeki hesapladığımız $u$ nedir? Çünkü $u$'dan $e$'ye oradan $w$'ya oradan da $f$'ye gitmek istiyorum. İlk geçişi matris $A$ yapar, ikinciyi $C$, üçüncüyü $A^T$.. Bildiğimiz şeyler bunlar ama bu yapıyı önümüzdeki probleme göre oluşturmak gerekiyor. Bahsettiğimiz matrislerin içini doldurmamız gerekiyor.

O zaman yapıyı tarif edelim. Mesela önce 1 no'lu düğüme bakalım, ona etki eden kuvvetler nedir? İk boyuttayız demiştik, o zaman bir yatay bir de dikey kuvvet olacak, en azından o düğüme etki eden tüm kuvvetler bu iki eksen bağlamında incelenebilir. Bilinmeyen $u$'yu bu fırsatla tanıştırıyorum, alttaki resimde mesela ikinci düğümdeki yer değişimini yatay ve dikey bileşenlerine ayırarak gösterebilirim,

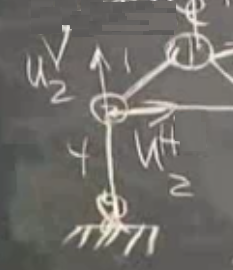
Bileşenler yatay yönde $u_2^H$, dikey yönde $u_2^V$. Bu yer değişimlerini, yatay, dikey her pim için yaparız, böylece, bir anlamda elimizdeki biinmeyen değişken sayısı ikiye katlanmış oldu. Artı, eksi olabilen tek bir $u$ öğesi yerine artık her düğüm için iki tane $u$ öğesi takip etmemiz gerekiyor.

Şimdi alttaki yere bağlı destek noktalarına bakalım; orada ne oluyor? Bu noktalarda ne sağa, ne sola, ne yukarı aşağı hareket var, çünkü oraları sabitlendi. O zaman $u_4^H = u_4^V = 0 = u_5^H = u_5^V = 0$. Toplam kaç tane bilinmeyen var? Altı tane. 1,2,3 düğümleri için ikişer tane, sabitlenmiş noktalarda yok, onlar biliniyor. Demek ki $A$ matrisim 5 x 6 boyutunda olacak. Bu yapı bize 6 tane $u$, 5 tane $e$, 5 tane çubuk kuvveti, ve 6 tane denge denklemi verecetir.

Fakat bu makaşkirişin üstünde durmak güvenli olmayabilir.. Bu püf noktası makaşkirişlere özel olarak devreye giriyor, ve konuyu daha ilginç hale getiriyor. Niye? Pür lineer cebirsel sebeplerle aslında, $A$ matrisi 5 x 6 boyutlarında, yani satırdan fazla kolon var, bu durumda $A u = 0$ denklemini çözen sıfır olmayan bir $u$ var, [1]'deki örnekte olduğu gibi. Bu arada $A$ matrisleri gerçek dünya örneklerinde rahatça satırdan fazla kolona sahip olabilir çünkü düğüm ekledikçe o sayı çarpı iki kadar kolon eklemek lazım, $A$ büyüyecek ve $A$ bağımlı kolonlara sahip olacak. Fiziksel dilde devam edersek sıfır olmayan yer değişimlerinin sıfır esnemeyi ima ettiği durumlar ortaya çıkabilecek.

Makaskiriş üzerinde bu neye benzerdi? Yer değişimi var, ama esneme yok. Alttaki gibi olabilirdi mesela,

Bu harekete tekabül eden $u$'yu hayal etmeye uğraşıyorum şimdi, yine 1, 2, 3 düğümleri aynı yerde olsun, ve ufak bir hareketi bir birimlik değerle temsil edersem (vektör içinde önce yatay sonra dikey değer gelecek şekilde),

$$ u = \left[\begin{array}{r} 1 \\ 0 \\ 1 \\ 0 \\ 1 \\ 0 \end{array}\right] $$

Yani sadece yatay yer değişimi oldu, dikey hiç olmadı. Fakat bazılarımız şimdi diyebilir ki "ama az da olsa dikey bir yer değişimi gözüküyor". Bu doğru, ama unutmayalım her şeye lineer bakıyorum, yaklaşıklama "birinci derece terimle" yapılıyor, o zaman mesela

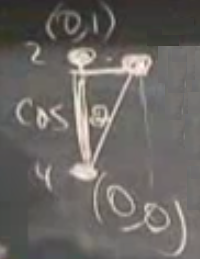
gibi bir durumda, $\theta$ kadar bir kayma var, çubuğun uzunluğu 1 diyelim, gelinen nokta neresidir? Yatay olarak bu yer değişim $\sin\theta$ kadar, dikey olarak $1-\cos\theta$. Şimdi ufak $\theta$ sözkonusu ise $\sin\theta \approx \theta$. Peki $1-\cos\theta$ yaklaşık olarak nedir? Her iki terim için de açılım yapalım, ve yüksek dereceki terimleri yoksayalım,

$$ \sin\theta = \theta - \frac{\theta^3}{6} ... \approx \theta $$

$$ 1-\cos\theta = 1 - (1-\frac{\theta^2}{2} ... ) = \frac{\theta^2}{2} ... \approx 0 $$

Eğer $\theta^2$ ifadesinin probleme dahil olmasına izin verseydim o zaman gayrı lineer bir problem elde ederdim. Bunu istemiyorum, yaklaşım lineer, o sebeple o terimleri atınca geriye üstteki sonuçlar kalıyor. Zaten gayrı lineerlige çoğunlukla ihtiyaç ta olmayabiliyor. Sonlu öğeler, yapılar, köprüler, alanım, araçlarım her ne ise umudumuz ve beklentimiz hep ufak $\theta$ varlığı ve problemin lineer olması. Ve lineer bir insan için $\theta^2$ sıfırdır. İşte bu sebeple üstteki $u$ içindeki bazı öğeler sıfır.

Devam etmeden ekleyelim, bir probleme gayrı lineerlik bazı durumlarda dahil olabilir; mesela geometrik gayrı lineerlik ile, üstteki problemde eğer $\theta$'ların çok büyük olmasına izin verseydim, o zaman $\theta^2$'i yok sayamazdım. Bu işleri zorlaştırırdı tabii, mesela bazı sonlu öğeler yaklaşımları buna izin verir, Abaqus'ta mesela bu tür hesap şekli desteklenir, o alanda ilk bakılan problemlerden biri Atlantik altındaki kablolara ne olurdu mesela, müthiş ilgi çekici problemler, bir diğeri araba kazası sırasında arabaların dış yapısına ne olur? O anda geometri değişiyor muhakkak, büyük yer değişimleri oluyor.. Bunlar gayrı lineer yaklaşım gerektiriyor.

Bizim problemde her şey lineer. Makaskirişin çok daha çetrefil olduğu problemler görürünüz belki ileride ama o durumda bile hala lineerlik varsayımı ile hesaplar yapmak mümkündür.

Bir soru daha sorayım; üstteki problemdeki şekil bozulma durumunu, deformasyonu (literatur bu duruma Ingilizce biraz garip olan "mechanisms" yani "mekanizma" ismini vermis) nasıl engellerim? Çünkü eğer azıcık sert bir rüzgar esse bu yapı küt diye aşağı düşecek değil mi? O zaman yapıyı nasıl stabil hala getiririm? Bu yapıyı tasarlıyor olsaydınız siz ne yapardınız? Bir tane daha çubuk ekleyebilirdim.

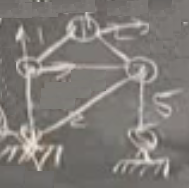
Sol alttan çapraz yukarı sağa doğru giden çubuğu yeni ekledim. Bu eklemeyi yapınca altı tane çubuk elde ettim, ve altı tane yer değişimi var, bu demektir ki $A$ matrisi 6 x 6 boyutunda. Bu durumda umut edilebilir ki $A$ matrisi artık eşsiz (singular) değildir, tersi alınabilir bir matristır, deformasyon olma durumu ortadan kalkmıştır.. Daha matrisi yazmadım tabii ama bir mühendislik kabaca olayı tartabiliyorsak üstteki makaskirişin artık stabil olduğuna kanaat getirebilirdik. Yapıyı daha da stabil yapabilirdim, mesela sağ alttan sol üst köşeye doğru yedinci bir çubuk ekleyerek. Bu durumda 7 x 6 matris elde ederim, hala deformasyon olmaz.

Ama şunu da belirteyim, 6 x 6 ya da 7 x 6 matris olsa da, $A$ matrisini yazmadan hala eşsizlik var mı yok mu bunu önceden söylemek mümkün değil. Sistem hala gayrı stabil olabilir (kıyasla 6 x 5 matris olsa mesela stabil olmama durumu kesindir). Acaba bol çubuklu ama stabil olmayan bir makaskiriş bulabilir miyim? Alttaki gibi bir yapı olabilir,

Üstteki örnek üzerinde egzersiz yapalım biraz (bu arada ders kitabında da [2] ek egzersiz örnekleri var). Bu yapıdan nasıl bir matris elde ederim? Çubuk sayısı nedir? Altı. Bilinmeyen sayısı? Sekiz. Çünkü hareket edebilen her pimde iki bilinmeyen, dört pim var, 4 x 2 = 8. O zaman $A$ matrisi 6 x 8 boyutunda.

Bu durumda kaç tene deformasyon olasılığı var? Büyük ihtimalle iki tane. Bir tanesi alt iki pimin yana kayması üst taraf beraber gelecek şekilde, diğeri alt iki pim yerinde durup üst iki pimin yana kayması. Bu iki seçeneğin bir kombinasyonu da ortaya çıkabilir muhakkak.

Bu örnek için de çubuk ekleyerek yapıyı stabil hale getirebilirim. En az iki tane çubuk ekleyerek bunu yapabilirim. Ama çubuk sayısı stabiliteyi garanti etmez, dikkat, çubukların nereye koyulduğuna dikkat etmek lazım, üst bölümde çapraz iki tane çubuk eklesem bu stabiliteyi garanti etmez, alt kısım hala deforme olabilir (hoca söylemedi ama çözüm herhalde bir çapraz çubuk alta, bir üste koymakla oluyor).

Aynı örneği değiştirelim, yere olan alt iki desteği siliyorum, ve hem alta hem üste iki tane çapraz çubuk ekliyorum.

Tekrar soralım, bu makaşkirişin esnemeden hareket etmesi mümkün müdür? $Au = 0$'in çözümü var mıdır sorusunu sorduk yine. Yapı artık havada uçuyor, normal olarak bu mümkün.. Üç şekilde bu hareket mümkün. Her şey toptan yatay sağa, ya da herşey dikey yukarı/aşağı gidebilir (translation). Üçüncü katı hareket şekli dönmedir (rotation), mesela sol alt pimi etrafında dönüş olabilir (diğer pimler etrafındaki dönüş bu pime etrafındaki bir dönüş artı yer değişimleri olarak indirgenebilir).

O zaman deformasyonlar ile katı gövde hareketlerini birbirinden ayırmak gerekiyor. Katı gövde durumunda deformasyon yok, her şey hareket ediyor. Katı gövde hareketi yeteri kadar destek olmadığı zaman, deformasyon ise yeteri kadar çubuk olmadığı zaman ortaya çıkar.

Dersi bitirmeden önce son bir soru sorayım? İlk baktığımız örnek için $C$ matrisi nedir? Hangi boyutdadır? 5 x 5 değil mi? Çünkü beş tane çubuk var, her biri için $C$ köşegen matrisi içinde bir öğe olacaktır. Bu öğeler üzerinden $w = C e$ formülü devreye sokulur, bu denklem her çubuk için geçerli olan Hooke Kanunudur. Gayet basit, İki $A$ ortasında bu $C$ var, ve Hooke Kanununu sisteme dahil ediyor.

Kaynaklar

[1] Bayramlı, Hesapsal Bilim, Ders 1-8

[2] Strang, Computational Science and Engineering

[3] Kassimali, Matrix Analysis of Structures, 2nd Ed