dersblog



Ders 23

Kitabımdaki 11. ve 12. bölümler hakkında biraz konuşalım şimdi. Onları tam detaylı işleyecek zamanımız kalmadı artık, ama o konulara da değinmek istiyorum. Nelerden bahsettik şimdiye kadar? Kaosta bahsettik, önce Lorenz sisteminde, sonra lojistik haritada kaosa giden periyot katlanmalı yolu, onun evrensel özelliklerini anlattık. Fakat hala işlemediğimiz bazı büyük konular kaldı. Mesela Lorenz sisteminde gidiş yollarının uzun vadede garip çekici (strange attractor) ismi verdiğimiz bir kümeye doğru yaklaştığını söylemiştik. Peki bu küme, bu şey nedir? Neye benzer? Onun bazı bilgisayar grafiklerini çizdik evet, ama garip çekicinin öz geometrisi hakkında fazla bir şey söylemedik. Bu derste bu konuyu işlemek istiyorum, çünkü 70'li yılların ortasında bu insanların kafasını oldukca karıştıran bir konuydu. O zaman bu ders ve bir sonraki için amacımız garip çekicinin geometrisini resmedebilmek olsun.

Bu konu için fraktal kavramından bazı fikirleri almamız gerekiyor, bu sebeple onlara hafif bir değineceğim. Kitabımda tüm bir bölüm bu konuya ayrıldı, detaylar için 11. bölümde fraktallara ve 12. bölümde garip çekicilere bakmak iyi olabilir.

Şimdi Lorenz sistemine ve onun garip çekicisine dönelim. Üstünde biraz düşününce paradoksal gelebilecek bir şey var; dedik ki birbirine yakın gidiş yolları birbirlerinden aşağı yukarı üstel hızda ayrılırlar, ki biz bu duruma "başlangıç şartlarına olan hassas bağlantı" ismini vermiştik. Diğer yandan dedik ki bir çekici sınırlanmış bir bölgede yaşıyor, büyük bir küre içinde olabilir, yani sınırları belli bir obje içinde ama bu bölge içinde gidiş yolları birbirinden üstel şekilde ayrılıyor.. bu nasıl oluyor? Soruyu şöyle netleştirelim: sonsuz şekilde genişleyerek (birbirine komşu gidiş yollarının yaptığı gibi) sınırlı bir bölge içine nasıl kalınabilir? Burada biraz abartma da kullanıyorum tabii, komşu gidiş yolları birbirinden çekicinin çapından daha fazla bir büyüklükte ayrılamaz. Ama sürekli genişleme ve aynı anda sınırlı bir yerde olma durumu geçerli, ve paradoksal.

Problem hakkında sezgi geliştirmek için faz uzayında olanların geometrisini düşünelim. Kısa cevap faz uzayında sürekli bir genişleme, katlanma, ve tekrar enjeksiyon denilen bir şeyin vuku buluyor olması. Bu pazarlamaçıların kullandığı türden kelimelerin ne anlama geldiğini anlatmadan önce önce çok daha tanıdık olabilecek birkaç resim çizmek istiyorum. Yemek, pasta, ya da kek pişirenlerinize bu resim tanıdık gelecektir, gerçi ben böyle şeyler pişirmeyi bilmiyorum ama biliyormuş gibi anlatıyorum :). Pişirme örneği için kullanacağımız pasta ya da hilal çöreği örneği. Bunları pişirmek için bir parça hamur alıyorsunuz, sonra merdane ile onu ezip, yassılaştırıp genişletiyorsunuz.

"Profosörümüz üşüttü mü acaba" diye düşünenleriniz olabilir, örneği biraz daha açayım. Hamur faz uzayını temsil ediyor, merdane ile ezme ve genişletme / esnetme ise vektör alanının bir kütle / demet başlangıç şartlarına yaptığıdır. Bu fikirden daha önce bahsetmiştik, bir demet başlangıç şartlarının yeni bir yere gitmesi, o yerde yeni bir kütle haline gelmesi, vs, ve şimdi ben iddia ediyorum ki kaotik sistemlerde bir çekiciye sıkıştırma yönünde yaklaşan gidiş yollarıyla alakalı ezme / düzleştirme hakkında düşünmek önemlidir. Bu sıkıştırma yönü üzerinden çekiciye gidilir, esnetme çekicinin üzerinde olan bir şeydir, bu sırada birbirine yakın gidiş yolları esneyerek birbirlerinden uzaklaşır.

Yani hamuru alıyoruz, düzleştirip esnetiyoruz, sonra katlıyoruz.

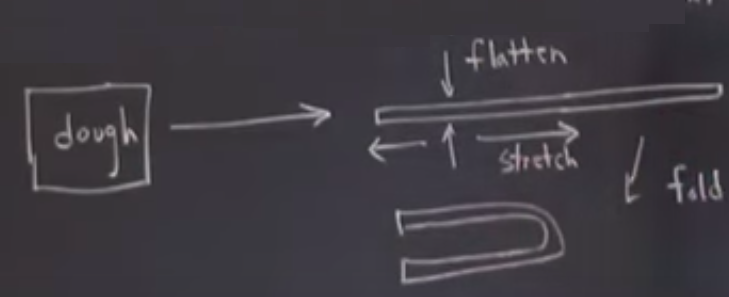
Tabii o görülen boşluk olmazdı, katlanan katmanlar tamamen birbirine yapışırdı, ama gösterim amacıyla öyle yaptım. Ardından tekrar enjekte adımına geliyoruz,

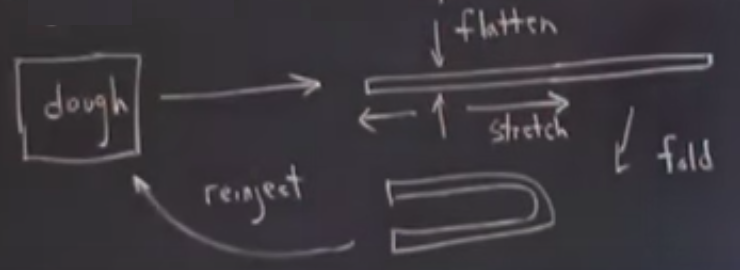
böylece başa dönmüş oluyoruz ve süreç tekrar başlayabiliyor, ama bu sefer daha değişik bir hamur var tabii, ve merdane, düzleşme, vs. oradan devam ediyor. Bu işlemi ardı ardına yapacağız, bu "hamur" üzerinde bir özyineli harita döngüsü olacak yani.

Göstermek istediğim bir katmanlı bir şeyle başladık, katladıktan sonra iki katman oldu, sonra katlanan obje katlandıktan sonra şimdi dört katmanı var. Her döngüde eldeki katman sayısı iki katına çıkıyor. Bazılarınız bilir belki yufka hamuru (phyllo dough) denen bir şey vardır, ya da Fransızların milfoy hamuru (mille-feuille [hoca bunu taklit Fransız aksanıyla söyledi]), bu tür hamurlarda neredeyse 1000 tane katman vardır. Bu demektir ki eğer katlaya katlaya gidilse 10 katlama sonrası $2^{10} = 1024$ bu katman sayısına erişilirdi.

Herneyse, iddia o ki bu acaip katmanlı yapının benzeri kaotik sistemlerin faz uzayında da aynen ortaya çıkıyor. Çıtlatmak istediğim mekanizma öyle bir şey ki bir kaotik sistemin faz uzayına akışımız üzerinden otomatik olarak çekicilerin fraktal yapısını üretmemizi sağlıyor. Sezgisel kavrayışın bir kısmı bu, detaylarını birazdan göreceğiz.

Bir diğer kısmı, eğer bu faz uzayında olan acaipliği (!) inanıyorsanız, bu sadece fraktalların değil, kaosun nereden çıktığını da aslında açıklar. Yani birbirine yakın iki başlangıç şartı düşünürseniz, mesela yine hamur örneğine dönersek iki seçtiğim noktaya bir renklendirici koymuş olsam, merdane, katlama, tekrarlama işlemleri ardından, ve diyelim 10 adım sonra renklendirici hamurun her tarafına yayılmış olurdu herhalde, ve bu başlangıçta yakın olan noktaların neredeyse herhangi bir yerde olabileceği durumu göstermiş olurdu. Anlatabiliyor muyum? Sadece fraktalların nereden geldiğini ima etmiyoruz, gidiş yollarının o ezilme, yayılma, vs. işlemi sırasında ayrılmasının yol açtığı enformasyon kaybının kaosla ilintilendirilen o tahmin edilmezliğin temeli olduğunu ima ediyoruz.

Şimdi size bir kitaptan [1] bazı resimler göstereceğim. Kitap 80'lı yılların başında çıkmıştı zannediyorum, ben hatırlıyorum, o zamanlar için yeni olan kaos, garip çekiciler, vs. konusunda bir kitap bulmaya uğraşıyordum, bu zor bir işti o zaman, başlangıç seviyesindeki birisi için rahat okunabilecek fazla kaynak yoktu. Ama bu kitap [1] tam da onu yapmaya uğraşan bir kitaptı, hatta yazarlar hiç matematiksel formül kullanmadan konuyu anlatmaya karar vermişler bunu sıkı bri şekilde takip etmişler, kitapta hiç formül yok, herşeyi görsel olarak anlatmaya uğraşmışlar. Görsel meyilli olanlarınız şimdiye kadar gördüklerimize farklı bir bakış açısı sağlaması açısından bu kitabı ilginç bulabilir. Ben pür görselci değilim tabii, formüllere inanırım, onları severim. Şimdi kitabın resimlerini görmeden önce kapaktaki resim hakkında bazı formüller göstermek istiyorum.

Resim Rössler çekicisi denen bir çekici. Onu bulan Otto Rössler bir biyokimyacıydı, 70'lı yılların ortasında zannediyorum, bizim şu anda sorduğumuz sorulara benzer sorular soruyordu, kaosun geometrisini nasıl irdeleriz? Garip çekicilerin o şekli almalarının sebebi nedir? Temel denklemlerini sıvı dinamiğini baz alarak yazan temebilim odaklı olan Lorenz'in aksine, Rossler panayıra gittiği zamanki bir hikayesini anlatıyor, orada pamuk helvası yapan bir makina görüyor, makinanın kolları var, önce sekizimsi, sonra sağdan solda değişik şekillerde hareket ediyorlar tabii bu sırada helvayı karıştırmış, katlamış, vs. oluyorlar. Herneyse Rossler bu makinayı seyrederken gördüklerinin kaosun geometrisi ile bir alakasının olabileceğini düşünmeye başlıyor. O gördüğü geometriyi canladıracağını düşündüğü başta biraz uydurukumsu bir denklem sistemi yazıyor ve bir garip çekiciyi ortaya çıkartıp çıkartamayacağını görmek istiyor. Şu denklemi yazdı ve bu denklem en basit garip çekiciyi içerir, hatta Lorenz sisteminden bile basittir. İçinde sadece bir (karesel, $xz$ terimi) gayrı-lineerlik vardır (Lorenz'de iki vardı),

$$ \dot{x} = -y -z$$

$$ \dot{y} = x + a y$$

$$ \dot{z} = b + z(x-c)$$

Bu denklemin doğabilimsel bir anlamı yok, uyduruk, $a,b$ dış parametreler. Rössler bir sürü parametre değerin denedi ve buldu, benim şimdi göstereceğim $a=b=0.2$, $c=5.7$. Bu değerler [1]'in kapağındaki şekli ortaya çıkartacak. 

from numpy import *
from matplotlib import *
from scipy import *
from pylab import figure, show, setp
from mpl_toolkits.mplot3d import Axes3D

def num_rossler(x_n,y_n,z_n,h,a,b,c):
    x_n1=x_n+h*(-y_n-z_n)
    y_n1=y_n+h*(x_n+a*y_n)
    z_n1=z_n+h*(b+z_n*(x_n-c))   
    return x_n1,y_n1,z_n1

a=0.2
b=0.2
c=5.7

t_ini=0
t_fin=32*pi
h=0.0001
numsteps=int((t_fin-t_ini)/h)

t=linspace(t_ini,t_fin,numsteps)
x=zeros(numsteps)
y=zeros(numsteps)
z=zeros(numsteps)
x[0]=0
y[0]=0
z[0]=0

for k in range(x.size-1):
    [x[k+1],y[k+1],z[k+1]]=num_rossler(x[k],y[k],z[k],t[k+1]-t[k],a,b,c)

fig = figure()
ax1 = fig.add_axes([0.1, 0.7, 0.4, 0.2])
ax2 = fig.add_axes([0.1, 0.4, 0.4, 0.2])
ax3 = fig.add_axes([0.1, 0.1, 0.4, 0.2])
ax4 = fig.add_axes([0.55, 0.25, 0.35, 0.5],projection='3d')

ax1.plot(t, x,color='red',lw=1,label='x(t)')
ax1.set_xlabel('t')
ax1.set_ylabel('x(t)')
ax1.legend()
ax1.axis((t_ini,t_fin,min(x),max(x)))

ax2.plot(t, y,color='green',lw=1,label='y(t)')
ax2.set_xlabel('t')
ax2.set_ylabel('y(t)')
ax2.legend()
ax2.axis((t_ini,t_fin,min(y),max(y)))

ax3.plot(t, z,color='blue',lw=1,label='z(t)')
ax3.set_xlabel('t')
ax3.set_ylabel('z(t)')
ax3.legend()
ax3.axis((t_ini,t_fin,min(z),max(z)))

ax4.plot(x, y,z,color='black',lw=1,label='Evolution(t)')
ax4.set_xlabel('x(t)')
ax4.set_ylabel('y(t)')
ax4.set_zlabel('z(t)')
ax4.set_title('Evolution')
plt.savefig('23_04.png')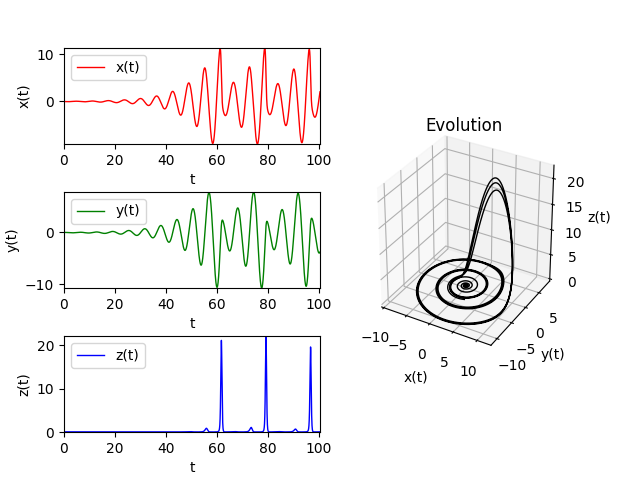

Prezentasyona dönelim, bahsettiğim kitap kapağındaki grafiğe bakalım şimdi,

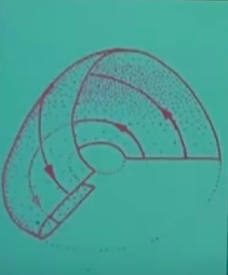
Dikkat edersek grafik Lorenz sistemin yarısı sanki. Lorenz grafiği bir iki kanatlı kelebek şeklindeydi, gidiş yolları bir kanattan diğerine sürekli gidip geliyordu.. Burada sanki bir kanat var sadece. Bunu daha detaylı tarif etmeye uğrasayım şimdi.

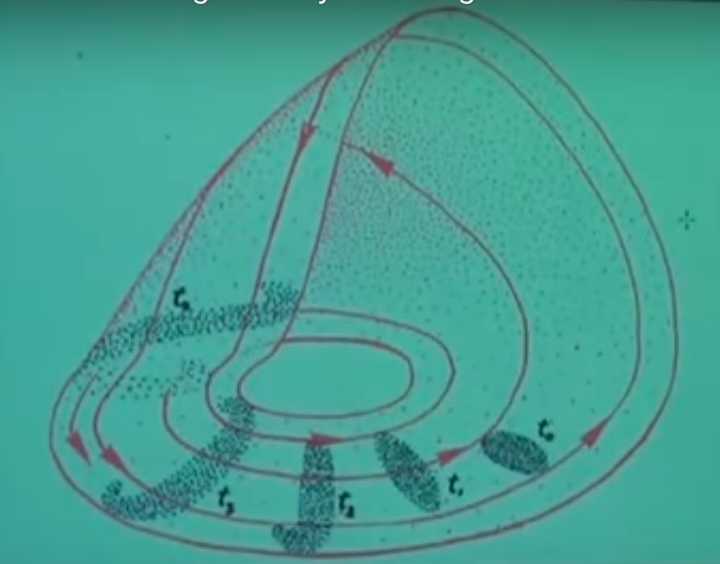
Bunlar elle çizilmiş resimler bu arada. Bu resimde çekici gösterilmiş, ve bakıyorsunuz, insanın resmi kavraması zaman alabiliyor. Kırmızı okları olan gidiş yollarını görüyoruz, ve $t_0$ zaman indisinde bir grup başlangıç konumu görüyoruz [gri bölge], ve o bölgenin sol kısmındaki başlangıç konumlarının gösterdiğim

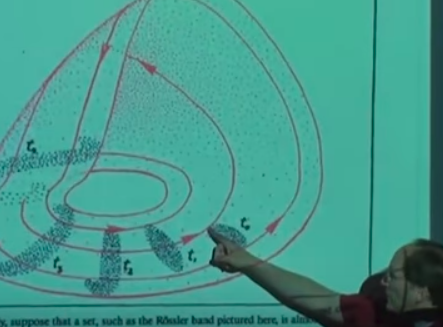
yoldan gittiğini görüyoruz. Yukarı doğru üçüncü boyuta doğru gittiğimize dikkat, bu kaos için niye en az üç boyut gerektiğini de açıkliyor bir anlamda. Aynı bölgenin sağ kısmının gösterdiğim

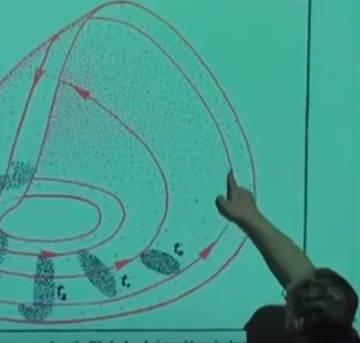
yolu takip ettiğini görüyoruz. Şimdi sol kısmın gidişini tamamen takip edelim,

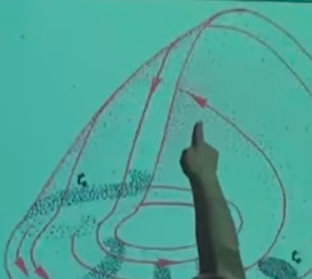
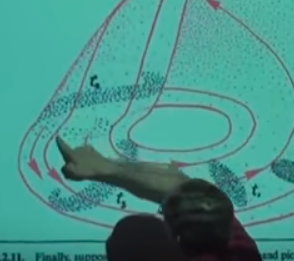
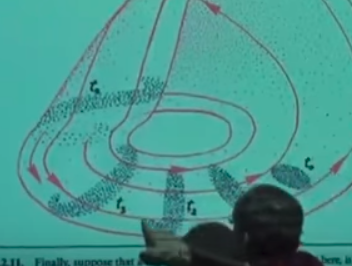
ve nihai olarak

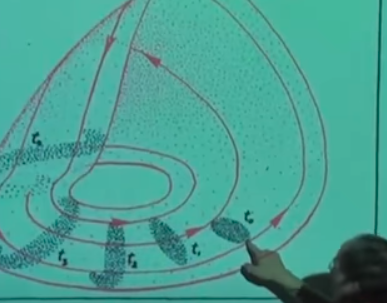
noktasına geliyoruz. Aynı bölgenin sağ kısmından başlasak,

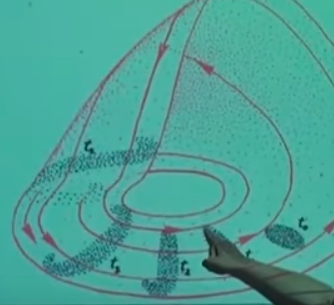
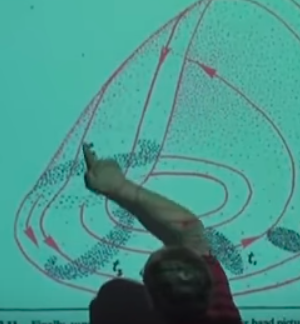
noktasına gelirdik. Vurgulamak istediğim ana nokta $t_0$'daki elipsoidimsi başlangıç noktaları $t_1$ noktasına geldiğimizde yana genişlemiş oluyorlar, ve dar yanlarından biraz daha basılmış hale geliyorlar, aynen hamurdaki tarif ettiğimiz durum gibi. Yol daha da ileri takip edilirse $t_2,t_3$'te şeklin deforme olmaya başladığını, daha da yayıldığını, vs. görebiliyoruz.

$t_4$ bölgesinde neler olduğu biraz kafa karıştırıcı olabilir. Tüm sistemin alt kısmı bağlamında oldukca düz bir satıh olduğunu görüyoruz, ama o yukarı gidişte, aşağı inişte, o bölgelerde ne oluyor? Gidiş yolları kendisiyle mi birleşiyor bir anlamda? Bir dal mı ortaya çıkıyor oralarda? O kısımdaki çizim zaten tam detaylı değil, o bölge hakkında biraz daha konuşalım o zaman.

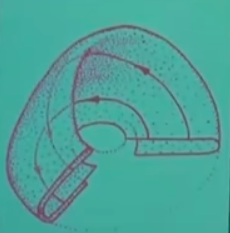
Kitabın alttaki sayfasında Rössler çekicisini parça parça nasıl biraraya koyabileceğimiz anlatılmış.

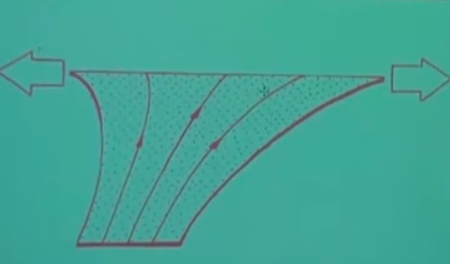
Önce bir yüzey düşünelim, o yüzeyde genişleme oluyor. O alttaki gidiş yolları sağa, sola ve yukarı doğru açılıp üstel hızda birbirinden uzaklaşıyor. Bu şekli alalım, ve ona uygulanan alttaki operasyon dizisine bakalım,

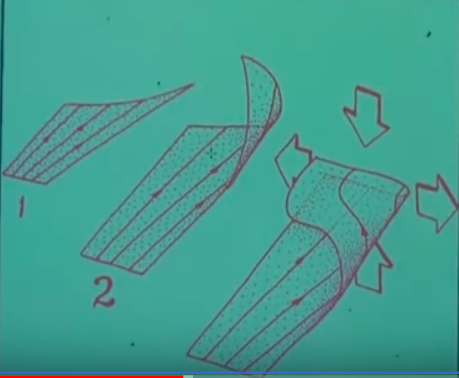
  1. adımda gidiş yolları yönünde bir esnetme yapılmış, ve aynı anda sağ tarafından bir katlanma başlatılmış, ta ki 3. adımda görülen hale gelininceye kadar. Ardından, 4. adıma bakınca,

o katlanan kısmın bir de kendisi üzerine katlandığını görüyoruz, hatta bu katlanma o kadar yassı bir haldeki neredeyse iki katman tek gibi gözüküyor. Şimdi o çok yassı katlanmalı kısım dönüp dönüp şuradaki

başlangıç kısmı ile birleşmeli, ama bu mümkün gözükmüyor, değil mi? Çünkü ana kurallardan birini hatırlarsak gidiş yolları birbirini kesemez, çünkü çözümlerin özgünlüğü şarttır, vs. Bu sebeple iki katman bir tek katmana yapıştırılamaz, bu diferansiyel denklemlerin özgünlük teorisini ihlal ederdi. Ama 5. adımda

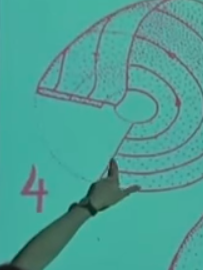
sanki bu olmuş gibi duruyor, ama o birleşmenin olmayacağını biliyoruz. Bu durum biraz daha açıklamaya ihtiyaç duyuyor. Kitap [1]'ın "fraktal mıkroyapı (fractal mıcrostructüre)" başlıklı kısmında bu açıklamayı bulabiliriz belki. İlk katlanma resmine dönelim,

Eğer devam edersek, bu katlanmış kesimleri başlangıç kabul edersek, onların da tekrar katlanacağını düşünmek gerekir ve alttaki durum ortaya çıkar,

Burada son uçta üst üste dört katman görülüyor. Aynı şekilde devam edersek sekiz katmana gelirdik,

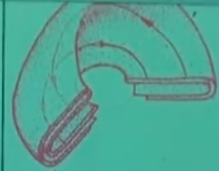
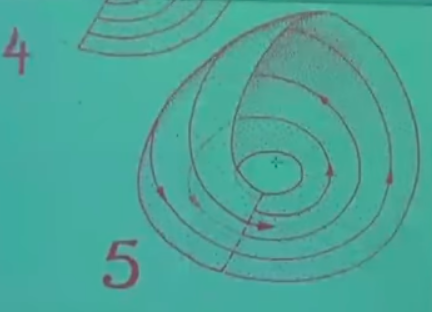
O zaman esas cevap aslında katmanların hiçbir zaman bir, iki, dört ya da sekiz olmadığı.. Elde her noktada sonsuz tane katman vardır, bu sonsuz katmanlar karmaşık bir süreç üzerinden birbirleri ile birleşiyorlar, ki bunu alttaki resim bir kesit üzerinden göstermeye uğraşmış,

Yani iki üstteki çekiciden bir kesit alıyoruz, ki buna Poincare kesiti (Poincare section) ismi de veriliyor [resimdeki dikey kesit], onun üzerinde bir kesit daha alıyoruz, buna da Lorenz kesiti deniyor. İşte bu noktada, o kırmızı gidiş yollarının Lorenz kesitini kestiği yerde kırmızı bölgelerin birbirine olan mesafeleri, aralardaki boşluklarda bazı kalıplar görmeye başlarız, mesela ortada büyük bir boşluk olur, aşağı gittikçe sonra ufak bir tane, sonra orta ölçekte bir tane, ondan sonra yine ufak.. Sadece bu boşluklara odaklanırsak grafiksel olarak alttakini görürüz,

Kitabın yazarları bu görüntüye bakıyorlar ve onlara analiz ya da topoloji dersinde öğrenmmış olabileceğiniz bir şeyi hatırlattığını söylüyorlar. Hatırlanan nedir? Elde bir çizgi var #1, onun üçte birini ortasından çıkartıyoruz #2, yani illa üçte biri olması gerekmiyor ama belli büyüklükteki bir orta parça, sonra elde kalan parçalarda da aynı işlemi yapıyoruz #3, ve bu şekilde devam edince mesela #5 seviyesinde elde edilen resmin üç üstteki resme benzediğini görebiliyoruz.

Bu kurgu Cantor kümesi denen şeyin oluşturulmasıdır aslında. Öğrenciler Cantor kümesini pür matematik derslerinde öğrenirler, ve doğabilimde bu kavramın karşılığı olmadığı ima edilir, fakat bu doğru değildir. Cantor kümesi garip çekicilerin temel bir özelliğidir. Ben mesela daha çiçeği burnunda bir matematikçi, bilimci iken bir kimyasal kaos konulu bir konferansa gitmiştim, ve orada bir konuşmacı kimyasal kaosu ölçtüklerini, ve sistemdeki çekiciyi grafiklediklerini söylüyordu, ve "tabii ki bu çekici Cantor kümesi üzerindeki bir kurdeledir" diyordu. Bunu duyunca şaşırdığımı hatırlıyorum, "ne dedin?". "Kurdele nasıl yani? Ne demek istiyor?" diye düşünmüştüm. Kurdele şimdiye kadar gördüğümüz yüzey, ve bu yüzey Cantor kümesi ruhunda, stiliyle katlanıyor. Herneyse o anlatımı yapan kişinin aklında [1] kitabındaki şekiller vardı tabii, benim o sıralarda bundan haberim yoktu.

Soru

Özyinelenen haritaları, mesela lojistik haritayı, üstteki anlattıklarımız ışığında görebilir miyiz?

Cevap

Evet kesinlikle. Bir sonraki derste o konuya daha derin dalacağız, ama özetlemek gerekirse, lojistik haritanın alttaki gibi grafiği vardı değil mi?

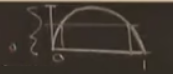
Bu grafiği sanki yatay ekseni alıp, esnetip, uzatıp ve parabol haline getirmek için eğdiğim bir işleme benzetebilirim. Yani lojistik harita da aslında esnetme, katlama yapıyordu, ama biz öne bu gözle bakmamıştık. Tekrar enjeksiyon durumu da var, yatay eksendeki değerler 0 ile 1 arası, esnetme, katlama sonrası elde edilen dikey eksende yine 0 ile 1 arasına eşleniyor. Tabii loijstik harita tam istediğimiz türden bir kaos yaratmayacak, çünkü lojistik harita tersine çevirilebilir (invertible) değil. Yani mesela dikey eksenden bir başlangıç değerim olsun, oradan başlayarak bir yatay çizgi çekeyim, o çizgi haritayı iki yerden keser, bu geriye gidemeyiz demektir. Ama diferansiyel denklemleri her zaman geriye doğru işletebilirsiniz, zamanı geri sarabilirsiniz yani. Yani lojistik harita üç boyutta görülen diğer kaos modellerine göre (mesela Rössler sistemi) biraz kabadır. Ama hala lojistik haritada pek çok "doğru şey" mevcuttur.

Soru

Sonsuz katmanların birleşmesi nasıl oluyor?

Cevap

Hayal etmesi zor değil mi? Bu konu hakkında Lorenz'in yazdıklarına bakmak iyi olabilir. Bir makalesinde [2] diyor ki ".. fakat bir çelişki gibi gözüken kavramın daha yakından incelenmesi kanımca iyi olur. Her ikisi de bir sarmal içeren iki yüzeyin birbirinin içine geçmesini bu teorilerde bir yere koymak zor çünkü iki gidiş yolunun birbirinin içine geçmesi mümkün değil". Burada Rössler çekicisinden bahsetmiyor çünkü o daha keşfedilmedi, onun örneğinde garip çekicinin gözünde olan gidişatın sonra diğer sarmala geçmesi, sonra geri, vs. durumu var. Devam ediyor "ama birleşmiş {\em gibi duran} yüzeyleri bir yere koymak, anlatmak zor değil". Yani sorduğu bu birleşmişlik görüntüsü nerede geliyor? Niye olduğunu açıklıyor, başlangıç şartları üzerinden bir hacim hesabı yapıyor, daha önce de gördük, Lorenz sisteminde hacimler üstel hızda küçülürler. Lorenz'in tanımladığı zaman adımları üzerinden 70 adımda sarmal etrafında bir tur atılıyor, bunun ardından hacim $7 x 10^{-5}$ kadar küçülmüş. Yani iki parçacık çok hızlı bir şekilde birleşebilirler.

Ama benim favorim şimdi gelen bölüm. Diyor ki "iki yüzey sadece birleşiyormuş gibi gözüküyor, ama aslında ayrı duruyorlar. Bir gidiş yoluna paralel olarak bir yüzeyi takip edince [ki daha önceki örnekte bizim de yaptığımız gibi] anlıyoruz ki her yüzey aslında aynı anda iki tane yüzey. O zaman birleşiyormuş gibi gözüktükleri yerde aslında dört yüzey var. Bu sürece devam edince, yok, aslında sekiz yüzey olduğunu görüyoruz, vs. Sonuçta şu sonuca varıyoruz, elimizde sonsuz çetrefillikte bir yüzey yapısı var, bu yüzeylerin her biri birleşlerden yüzeylerden ya birine ya ötekine müthiş yakın ".

Bu "sonsuz yüzeyler yapısı (infinite complex of surfaces)" sözüne dikkat. Lorenz bunları fraktallerin ortaya çıkmasından yıllar önce söylüyor. Ne olduğunun çok iyi farkında. Dersimizde bahsettiğimiz herşey bir anlamda burada pat diye ortaya kondu. Tabii hayal edebiliriz ki Lorenz'in zamanındaki bilimciler bunları okuyup hiçbir şey anlamamışlardır. Yazılanlar son derece açık, ama Lorenz diyagram çizememiş, o zaman bilgisayarlar dandik. Ama herşey zihninde görüyor. Lorenz'in büyüklüğü buradan geliyor.

Cantör kümesinin boyutları

Bu boyutları kesin olarak hesaplamak mümkün. Cantor kümesini düşünmek için, daha önce yaptığımız gibi, 0 ve 1 arası bir kapalı aralık alırız, "kapalı" diyorum çünkü son noktalar da aralığa dahil. Sonra aralığın orta 1/3'ünü çıkartırım, bunu yapmaya devam ederim,

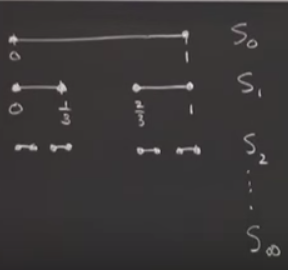
Matematikçi Cantor 1800'lu yılların başında kendi araştırmaları için buna benzer şeyler yapıyordu, garip çekiciler, kaos, vs. bunlara bakmıyordu tabii, bu konular o zaman daha mevcut değildi. Poincare bazı işler yapmıştı ama daha konu işin başındaydı.

Neyse, şimdi Cantor'ün sıraladığı üstteki yapıları ayrı ayrı kümeler olarak görelim, baştaki küme $S_1$, sonraki $S_2$, vs.. Ve bizim içinden çıkartma ile yarattığımız bu kümelerin bir limitteki kümeye gittiğini düşünelim, ona $S_\infty$ diyelim. Bu kümeyi çizmeye cüret etmiyorum tabii (!). Ama bu $S_\infty$ kümesi Cantor kümesi.

Bu küme içinde ne vardır? İlk akla gelebilecek cevap "hiçbir şey" olabilir. Ama bu doğru değil. Aslında orada bir sürü şey var. Bunlardan bazılarını sayabilir misiniz? [öğrenci sıfır diyor]. Doğru, sıfır noktası. Bu noktayı bölüm çıkartma sırasında hiçbir zaman çıkartmıyorum. Bitiş noktalarını da çıkartmıyorum, mesela 1/3, ya da sürecin her hangi bir basamağında yaratılmış herhangi bir üç nokta hep kümede kalıyor, çünkü üç noktaların arasındaki şeyleri çıkartıyorum sadece. Öğrenciler bunu duyunca "tamam sadece üç noktalar kaldı o zaman" diyor, bu durumda Cantor kümesi "sayılabilir" olur. Kaç üç noktası olduğu da belli, ilk başta 2, sonra 4, sonra 8, vs., daha doğrusu basamak $n$'deki üç nokta sayısı $2^n$. Bu sayı da sonsuzluğa gidiyor ama sayılamaz bir sonsuzluk değil bu, mesela reel sayılar gibi değil. Çoğu öğrencinin sayılabilir vs. sayılamaz kümeler hakkında bilgisi olmuyor, [1]'de bu iki kavram detaylı olarak işleniyor. Biz bu konuya girmeyeceğiz, onun yerine boyut kavramından bahsedeceğiz.

Cantor kümesinin bazı ana özellikleri

1) Toplam uzunluğu sıfıra eşit: Burada terminolojinin etrafından dolanıyorum biraz, çünkü pür matematik konusunda reel analiz dersinde değiliz, doğru kelime uzunluk değil ölçüt (measure) olmalı ama neyse. Biz bu ölçütü, ya da uzunluğu şu şekilde belirteceğiz, $|S_0| = 1$, yani $S_0$'in uzunluğu 1 olacak, $|S_1| = 2/3$, $|S_2| = 4/9$. Buradaki kalıbı daha iyi belirtmenin bir yolu $|S_n| = \left(\frac{2}{3}\right)^n$ çünkü her basamakta eldeki uzunluğu alıyorsunuz, onun içinden 1/3'ünü çıkartıyoruz, geri kalan her adımda 2/3. Tabii $n \to \infty$ iken bu uzunluk sıfıra gidiyor. İşte bu anlamda Cantor kümesinin uzunluğunun, her ne kadar uzunluk kelimesi net tarif olmasa da, sıfıra gittiğini söylüyoruz. Bu son noktada, Cantor kümesinde artık fazla bir şey kalmamış. Eğer herhangi bir parça kalmış olsaydı bir uzunluktan bahsedilebilirdi.

2) Evet, uzunluk sıfır ama küme içinde sayılamaz çoklukta nokta var (ya da basit tarifle sayılamaz). Bu demektir ki bu kümedeki ögelerle reel sayılar kümesi ögeleri arasında birebir eşleme yapabiliriz. Yani başlangıçtaki 0 ile 1 aralığı kadar burada öğe var. Bu hakikaten paradoksal. 0 ile 1 arasındaki öğeleri çıkartarak Cantor kümesine ulaştık, öyle ki uzunluk sıfır haline geldi, ama hala o başlanılan aralıktaki ile aynı sayıda öğe var. Bunu kabul etmek zor geliyor ama ispatı mümkün, Cantor kümesinin $x \in [0,1]$'daki tüm sayıların 3 bazındaki halinin sadece 0'lar ve 2'ler (ama 1'ler değil) kullanılarak yazılabileceğini göstereceğiz.

3) "Kendine benzerlik (self-similarity)" - içinde herhangi bir sayıda daha ufak olacak sekilde kendi kopyasını barındırır. Bununla ne demek istiyorum? Kumeyi olustururken cizdiklerimi tekrarlayayim.

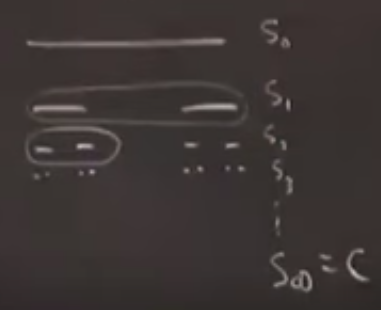
$S_0,S_1,...$ diye gidiyor ta ki Cantor kümesine gelinceye kadar. Ama ondan önce o sonlu basamaklardan birinde olanları düşünelim. Mesela $S_2$'nun sol parçasına bakalım. Bu parçanın yapısı neye benziyor? Aynen üstündeki yapıya benzemiyor mu? $S_2$ bir üstündeki yapının, $S_1$'in ufaltılmış hali (üçte biri). Bu ufaltılma tüm basamaklar için aynı şekilde geçerli, $S_4$ ile $S_3$ arasında, $S_8$ ile $S_7$ arasında, vs.

Şimdi bu argümana devam edersek, bu şekilde ufalta ufalta Cantor kümesi $S_\infty$'a geldik. Onu üçte bir oranında ufaltınca $C_{\infty+1}$'in sol kısmını elde ediyoruz, yani $\infty+1 = \infty$ olduğuna göre yine $C_\infty$'in sol kısmını elde ediyoruz. Yani Cantor kümesinin sol (ya da herhangi bir) kısmi yine Cantor kümesinin kendisinin ufaltılmış hali. İşte "kendine benzemek" ile bundan bahsediyorum, küme farklı ölçeklerdeki kendi kopyalarını yine kendi içinde barındırıyor.

4) Boyutu (bazıları benzerlik boyutu der ama biz sadece boyut diyelim) $\frac{\ln 2}{\ln 3} = 0.63..$. Yani Cantor kümesinin boyutu 0 ile 1 arasındadır. Boyut sıfır değil, sıfır boyut tek bir noktanın boyutudur. 1 değil ki bu sonlu sayıda noktanın boyutudur. Ya da.. sayılabilir noktaların kümesi.. [hoca düşünmeye başladı, tam emin değil]. Rasyonel sayıların boyutu sıfır mı acaba? Bilmiyorum. Sayılabilirliğin her zaman sıfır olup olmadığına bakmak lazım. Herneyse gördüğümüz küme 0 ile 1 arasında. Bir eğrinin boyutu 1 olurdu, bir düz çizgi 0 ile 1 arası yine.

Bunu niye söyledik? Kendine benzeyen bir nesnenin boyutu ne demektir? Boyut kavramına pek çok farklı bakış açısı vardır. Şimdi kullanacağımız bu problem için en rahat olanı. Şimdiye kadar çoğunuz boyut sözünü bir noktanın yerini belirtmek için gereken eksen sayısı bağlamında gördünüz herhalde. Mesela "dünya üç boyutlu" deriz, çünkü fiziksel dünyada yer belirtmek için, mesela bu odada, yerden olan yükseklik, sizden [öğrencilere] olan uzaklık, ve [sol tarafına işaret ediyor] duvardan olan uzaklık lazım. Ama Cantor kümesinde nasıl yer belirtiriz? Sadece tek bir sayı kullanamayız, bu sadece orijinden olan uzaklık olurdu, yeterli değil, çünkü o zaman küme tek boyutlu demiş olurduk. Bu boyutun iyi bir tanımı olmaz, fraktal nesnelerine iyi bir genelleme sağlamıyor, farklı fraktalları birbirinden net şekilde ayırmak için iyi bir kıstas sağlamıyor.

Bu çerçevede kullanılan, ve fraktal olmayan diğer kullanımlara da indirgenebilen, bir başka tanım şudur. Bir karesel alanı düşünelim. Bu tür bir alanın da kendine benzer olduğu iddia edilebilir, mesela onu $r = 3$ boyutunda küçülteyim (Cantor kümesi ile bağlantı kurmak için üç seçtim), ve küçültme tabii ki her yönde. Bu ufak kare büyük olanın dokuzda biri olur,

Bu dokuz sayısı nereden geldi? Üç ile bağlantılı olarak tabii, $r = 4$ olsaydı 16 olurdu. 5 için 25, vs. Yani ufaltma ölçeği ne ise, onun karesi kadar kopyayı orijinal içine sığdırabilirim. Yani $m = r ^2$. Bu üstel, yani 2 kritik sayı ve karesel alanın boyutunu tarif ediyor. Değil mi? Tahtada çizdiğim bu kare iki boyutlu, işte üsteldeki iki buradan geliyor. İşte bir kare kadar basit olmayabilecek kendine benzeyen objeleri tarif için kullanılan genelleme şöyle, eğer kendine benzeyen objem için elimde bir ölçekleme ilişkisi var ise ki $m = r^d$ seklinde, $d$'ye boyut diyeceğim, ya da benzerlik boyutu.

Bu tanımı Cantor kümemize uygulayalım. Biraz önce dedik ki Cantor kümesini alıp 3 ölçeğinde küçültürsek, kendisinin sol kısmını elde ederiz. Bu demektir ki $r=3$ ise $m=2$. Değil mi? Sol parça diğer iki parçanın yarısı kadardır. Bu sayıları biraz önceki formüle verirsek,

$$ m = r^d \Rightarrow d = \frac{\ln m}{\ln r} = \frac{\ln 2}{\ln 3}$$

İşte bu sebeple boyut kesirli (fractional).

Bu tür hesabı diğer kendine benzeyen nesnelere de rahatlıkla uygulayabiliriz. Kitabımdaki fraktalları anlatan bölümde bu örnekler bulunabilir.

Umarım bu konu hakkında ana yemeğin tamamın veremesek te bir tat sağlamış oldum. Daha fazlası için kendiniz konu hakkında okuma yapabilirsiniz. Bir sonraki derste önceden kısaca değindiğimiz iki boyutlu harita, Henon haritasından bahsetmek istiyorum, orada esnetme, katlanma işlemlerini daha yakından göreceğiz, ve bu işlemlerin fraktal yapıya olan etkilerini anlamaya çalışacağız. Hala fraktalları sayısal olarak görmedik, Lorenz sisteminde görmedik, bugün de göstermedim, ama Henon haritası bu fikirlerin hakikaten somut olarak işlediğini zannediyorum ispatlayacak.

Kaynaklar

[1] Shaw, Abraham, Dynamics, The Geometry of Behavior

[2] Lorenz, Deterministic Nonperiodic Flow, http://math.bu.edu/people/mabeck/Fall14/Lorenz63.pdf


Yukarı