Ders 21

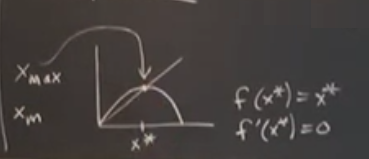
Şimdiye kadar lojistik haritadan bahsettik, pürüzsüz bir fonksiyon ve tek maksimumu vardı. Böyle bir fonksiyonu özyineli şekilde çağırınca stabil bir sabit noktadan stabil periyot 2 durumuna, oradan periyot 4'e geçişler oluyor, periyotlar katlana katlana gidiyor. Ve bu periyot katlanmaları parametreyi değiştirdikçe daha hızlı olmaya başlıyor, ve bir kritik parametre değerinden sonra kaos başlıyor. O noktadan sonra periyotluk ve kaosun içiçe olduğu pencereler görüyoruz, bir biri bir ötekinin olma durumu daha doğrusu... Şimdi bu olanların, kaosa varan periyot katlayan geçişlerin evrensel özünü kavramaya uğraşacağız. Tekrar normalizasyon analizinin bu anlayışı bize sağlamasını bekliyoruz.

Bir önceki derste Feigenbaum'un bulduğu iki sabitten bahsetmiştim. Bunlardan biri 4.6 civarında olan parametre eksenindeki ölçeklemeyi kontrol eden $\delta$, diğeri -2.5 civarındaki dikey yönde tırmık çatallaşmasının bir tür genişliğini kontrol eden $\alpha$ parametresi. Bu iki parametrenin nereden geldiğini anlamaya çalışacağız, ayrıca daha derin soru olan niye bu parametrelerin evrensel olduğunu anlamaya çalışacağız. Niye aynı niteliksel şekle sahip olan haritalar aynı niceliksel rakamlara bağlı? Niceliksel bir şey niteliksel bir şeyden nasıl doğabiliyor?

İlk önce süperstabil sabit nokta ve çevrimlerinin ne olduğunu tanımlamamız lazım, çünkü Feigenbaum analizini bu kavramları kullanarak yapmış. Bu arada hatırlarsak bir haritayı $x_{n+1} = f(x_n)$ üzerinden tanımlıyorduk, ve $x^\ast$ sabit noktası $f(x^\ast) = x^\ast$ olan yer idi. Lineer stabilite analizi ile sapmalara bakmıştık, $x_n = x^\ast + \eta_n$ tanımlamıştık, ki $\eta_n$ çok küçük bir sayıdır, ve görmüştük ki $\eta_n$ belli bir formüle sahip / formülü takip ediyor. O sırada lineerizasyona bakıyorduk, yani $\eta_{n+1} = f'(x^\ast) \eta_n + ...$, noktalı yerde yüksek dereceli terimler olacak.. Ve buradan eğer $|f'(x^\ast)| < 1$ ise $x^\ast$'in lineer olarak stabil olacağına sonucuna varmıştık. Bu durumda sapmalar üstel hızda çürüyorlardı. Lineer stabilite için kriterimiz buydu.

Fakat stabilitenin olması daha iyi bir şart $|f'(x^\ast)|$ sadece 1'den küçük olması değil, sıfıra eşit olmasıdır. Süperstabilite ile demek istediğimiz budur. Süperstabilite ile söylenmek istenen ise $x^\ast$'e yakınsama üstelden bile daha hızlı. Ama bu nasıl oluyor, üstelden hızlı yakınsama nasıl oluyor? $\eta_{n+1} = f'(x^\ast) \eta_n + ...$ ifadesine tekrar bakarsak, eğer $f'(x^\ast)$ sıfır ise formüldeki $f'(x^\ast) \eta_n $ terimi yokolur. O zaman neler olduğunu anlamak için noktalı kısımdaki yüksek dereceli terimlerin ne yaptığını anlamamız lazım. Taylor formülünü kullanalım,

$$ \eta_{n+1} =\frac{1}{2!} f"(x^\ast)\eta_n^2 + ... $$

Direk $f"$'a atlandı çünkü ana formüldeki yokolan terim yüzünden. Üstteki noktalı yerde $\eta$'nin küpsel ve daha yüksek katları olacak.

Üstteki ifadede bir sonraki $\eta$'nin bir önceki $\eta$'nin karesine oranlı olduğunu görüyoruz. Bu çok, çok hızlı yakınsamaya sebep olur. Bu tür bir yakınsamayı daha önce irdelememiş olanlarınız için zihinde canlandırma yapabilmek için şöyle açıklayayım: formüldeki sabitleri vs. yok sayalım, sadece $\eta_{n+1} = \eta_n^2$ ne yapar onu anlamaya uğraşalım. Bir sayıdan başlayalım, mesela $\eta_1 = 10^{-1}$. Bir hesap sonrası $\eta_2 = 10^{-2}$ olur, 10 katı bir çarpım alınmış oldu, yani orijine doğru gidiyoruz $10^{-1} = 1/10$, $10^{-2}=1/100$ ve şimdi 10 kat daha yakınız. Ama şimdi $\eta_3$ ne olur ona bakalım, $\eta_3 = 10^{-4}$, yani 10 değil 100 kat daha yakınız. $\eta_4 = 10^{-8}$, 10 bin kat daha yakınız. Gördüğümüz gibi müthiş hızlı bir şekilde orijine gidiyoruz. Uzun vadede sonuç sıfır olacak tabii. Bu tür bir yakınsamaya lineer olana kıyasla "karesel yakınsama (quadratic convergence)" ismi de veriliyor. Süper hızlı, neyse, süperstabil bir sabit noktanın yakınında bu tür şeyler olur.

Eğer sayısal metotlar (numerical methods) dersi aldıysanız bu derste Newton'un Yöntemi, ya da Newton/Rapson Yöntemi diye bir metot öğretildiğini görebilirdiniz, bu metotla bir denklem sayısal olarak çözülür, ve herkes Newton'un Yöntemi'nin çok hızlı işlediğini bilir çünkü bu yöntem aranan çözümü Newton yinelemesi / aramasının bulacağı bir süperstabil sabit noktaya çevirir. Metotu görenler bir geriye bakıp düşünürse metotun bu söylediğimi yaptığını anlayacaklardır.

Eğer örümcek ağı diyagramı bazında düşünürsek, sabit noktaları fonksiyon grafiğinin 45 derece yatay köşegeni kestiği yerde ortaya çıktığını biliyoruz. Eğer bu kesişimin olduğu yerde grafiğin eğimi sıfır ise

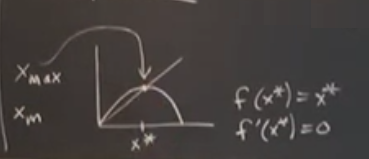
bu bir süperstabil sabit nokta olurdu çünkü orada $f'$ sıfır, bir maksimum var, ayrıca $f(x^\ast)=x^\ast$ sabit nokta olduğu için. Yani bir kritik nokta, maksimum ya da minimum, eğer köşegende geçiyorsa, orada süperstabillik var demektir. Kesişme noktasına $x_m$ diyelim.

Peki ya çevrimler? Süperstabil bir p-çevrimi nerede ortaya çıkar? $x_m$ noktasının $f$'nin $p$'inci özyineliminin sabit noktası olduğu yerde ortaya çıkar. Bir p-çevriminin $f^p$'nin sabit noktası olduğunu söylemiştik. Bu prensibi ta Lorenz haritalarından bahsettiğimiz zamandan biliyoruz. Ya da $x_m$ p-çevrimine dahil olan noktalardan biri. Bir örnek süperstabil bir 2-çevrimi olabilir, örümcek ağı diyagramı alttaki gibi olabilir,

2-çevrimdeki noktalardan biri maksimum noktası, diğeri başka bir yerde, ve onların arasında gidip geliniyor. Her periyotta süperstabil çevrimler olabilir bu arada. Rahat çalışılabilen şeyler onlar, çünkü onları sayısal olarak hızlı bir şekilde bulmak mümkün. Herhalde Feigenbaum'un onları tercih etmesinin sebeplerinden biri bu sayısal hesap rahatlığı idi. Mesela periyot katlanmasının tam nerede olduğuna bakmadı, bu bölgelerde yakınsama yavaş olacaktı. Süperstabilite yakınsamanın hızlı olduğu yerler.

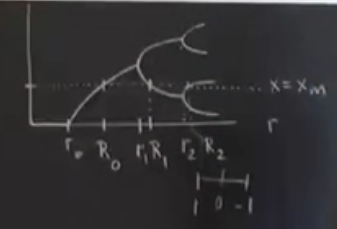
Şimdi Feigenbaum'un diyagramına tekrar bakarsak, bazıları bu diyagrama incir ağaçı (fig tree) diagramı diyor, ki bu yörünge diyagramının kaosa girilmeden önceki bölümü. Göstermek istediğim $r$'nin süperstabil değerlerinin bu resmin neresinde olduğunu göstermek. Onları bulmak için haritanın maksimumunun nerede olduğuna bakmak lazım.

Bu çizgi her periyotta dallardan birini mutlaka keser. Çünkü, daha önce dediğimiz gibi, her periyotta bir süperstabillik var. Devam edelim, $x_m$ çizgisinin haritayı ilk kestiği yere $R_0$ diyoruz. Terminoloji şöyleydi, $r_n$, stabil $2^n$ çevrim doğuyor, $R_n$ $2^n$ çevrim süperstabil. Yani büyük harfle $R_n$ bir süperstabil sabit nokta var demek.

Soru

Herhangi bir periyot büyüklüğü için süperstabilliğin olduğu tek bir $r$ noktası var değil mi?

Cevap

Bu kaosun başladığı ana kadar doğru. Bu noktadan sonra aynı periyotun farklı pencereleri olabiliyor. Mesela birden fazla 4-periyot penceresi olabiliyor, ya da 6-periyot, vs. Ama herhangi bir pencere için, evet, orada sadece bir süperstabil nokta var. Niye? Resimde niye olduğu görülüyor belki. Bir çevrimin hayatını düşünelim, $f'=1$ olduğu zaman, çoğunlukla teğet bir çatallaşmayla, doğuyor, biz $r$'yi değiştirdikçe hayatına bir süre devam ediyor, bir yerde $f'=0$ oluyor, ve "stabil" hayatının sonunda, periyot katlandığında, $f'=-1$ olacaktır. Yani hayat özdeğer 1'de başlıyor, periyot katlanması -1'de oluyor, ve arada bir yerlerde özdeğerin 0 oluyor, orada genç zinde olunduğu yer, orada süper stabiliz, sizin gibi [hoca öğrencileri gösteriyor], ben -1'e doğru gidiyorum [sınıf gülüyor]. Diyagrama tekrar bakarsak, $r_0$'da doğum (bu nokta gerçi teğet çatallaşmada doğmuyor ama neyse), $R_0$'da süperstabil oluyor, $r_1$'da periyot katlanması.. Katlanma noktasından sağa doğru bir gayrı-stabil dal da var aslında ama onu göstermedik.

Benzer şekilde $R_1$ olarak gösterdiğim yerde süperstabil bir 1-çevrim var, sonra periyot 4'un ortaya çıktığı yer, oraya $r_2$ dedik, ve $r_2$, vs. Göstermek istediğim büyük $R$'ler küçük $r$'lerin arasında / ortasında.

Soru

Maksimum noktasının p-çevrimdeki noktalardan biri olması onu otomatik olarak süperstsabil yapar mı?

Cevap

Evet. Niye? Bir 2-çevrim üzerinde göstereyim, ki bu argüman tüm çevrimlere genelleştirilebilir. Diyelim ki 2-çevrime ait olan bir $x$ noktam var. O zaman $f^2(x) = x$ olacaktır, çünkü $x$ periyot 2 noktası yani $f^2$'nin stabil noktası. Şimdi sorabiliriz, $x$ $f^2$'nin bir süperstabil noktası mı? Bunu kontrol etmek için türeve bakmak lazım.

$$ (f^2)' = \frac{d}{\mathrm{d} x} (f(f(x))) = f'(f(x))f'(x) $$

Süperstabillik şartı $(f^2)'$ sıfır olmalı, ki bu $f'(f(x))f'(x)=0$ demektir, bunun olması için de çarpanlardan birinin sıfır olması lazım, ya $f'(f(x))$ ya da $f'(x)$, yani maksimum bu carpanlardan birini ya da otekini sifir yapacak olan $x$. Bu durumda sifir olmakla maksimum ayni sey cunku tek tepeli fonksiyonlari inceliyoruz, o sebeple maksimum 2-cevrimlilige sahip olmali.

Daha önce dedik ki $R_n$'ler $r_n$'lerin arasında, yani $r_n$ ve $r_{n+1}$ arasında. Bazılarımız merak edebilir ki grafiktek soldan sağa giderken, kaosa yaklaşır ve periyot katlanmaları sürekli, daha hızlı, daha hızlı artarken $R_n$'ler nasıl oluyorda $r_n$'ler arasına düşecek şekilde aynı ölçeklenme kuralını takip ediyor? Dedik ki $r_n$'ler Feigenbaum'un oranına uygun şekilde yakınsıyor. Öğreniyoruz ki $R_n$'ler de bu şekilde davranıyor - bu pek şaşırtıcı değil herhalde - yani ardı ardına gelen $R_n$'ler arasındaki boşlukların büyüklüğü de geometrik hızda küçülüyor, ve sonuşurda (yani kaosa yaklaşıldığı durumda, $n \to \infty$), $\delta \approx 4.669..$ oluyor.

Tekrar normalizasyon fikrinin temeli şudur: üstteki inciri ağacı resmi farklı ölçeklerde kendine benziyor (self-similar). Fraktallardan kabaca bahsetmiştik, tam olarak ne olduklarını matematiksel olarak tanımlamamıştık ama şu şekilde tarif edebiliriz;

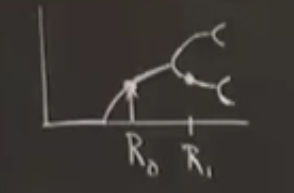
Diyelim ki üstteki grafikteki durum var, ve $R_0$ noktasındaki bir karıncayız. Bir gidişat var ve biraz daha ileri bakınca karınca bir ikiye ayrılma durumu görüyor. Şimdi o ayrılan dalların birinde $R_1$ noktasında bir diğer karınca olsun, bu karınca da ileri bakınca benzer bir ayrılma görecek. $R_0$ ve $R_1$'den görülenler çok farklı değil, ama bir bakıma ikinci olay daha ufalmış, daha ufak ölçekte oluyor. Yani görüyoruz, birinci dallar daha büyük, ikinciler daha küçük. Daha net olarak belirtmek gerekirse, $R_0$ ve $R_1$ benzer, ve onları karşılaştırmak mümkün, bunun için bir noktayı diğerine doğru tekrar normalize edebiliriz, yani birinin ölçeğini ayarlayarak öteki ile karşılaştırılabilir hale getirebiliriz. Bunu daha aciklamaya ugrasayim.

$f(x,R_0)$ grafiğini çizelim ve onu başka bir grafik ile birazdan karşılaştıracağız. $R_0$'da bir süperstabil sabit nokta var demiştik, $R_0$'in tanımı buydu.

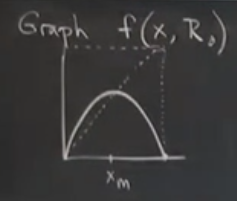
Köşegen çizgi maksimum noktadan geçiyor. Bu grafikte köşegeni kapsayacak şekilde bir kare çizmek faydalı, üstte görülüyor.

Bu grafiği $R_1$ için olan grafikle karşılaştıralım. Bu grafikler birbirine benzemelidir, bir farklılık haricinde. Bu farklılık nedir? $R_0$ süperstabil bir sabit nokta idi. $R_1$ ise periyot 2 özelliğinde bir süperstabil sabit nokta (2 çevrimde süper stabil bir nokta). O zaman uygun karşılaştırma stili nedir? Eğer $R_0$'da $f$'yi karşılaştırmak istiyorsam $R_1$'de onu ne ile karşılaştırmalıyım? $f$'mi ... ? Yoksa $f^2$ mi? Bu daha iyi olur değil mi? Çünkü iki üstteki grafikte sağ üstte görüldüğü gibi bir 2-çevrim var orada, eğer $f^2$'ye bakarsam $R_1$'in $f$'yi kestiği nokta bir süperstabil sabit noktadır, $f^2$ için tabii. O zaman karşılaştırma yapılacak şey $f$ değil $f^2$, daha doğrusu $f^2(x,R_1)$. Burada anahtar nokta $x_m$'in her iki harita için de süperstabil bir sabit nokta olması.

Şimdi $f^2(x,R_1)$ grafikleyelim. Hatırlarsak bu fonksiyonun iki tepeli bir şekli vardı, ve maksimum noktası 2-çevrimdeki noktalardan biriydi, bunun anlamı şudur, bu grafikte de köşegeni çizince o köşegen aynı şekilde $x_m$'den geçmeli.

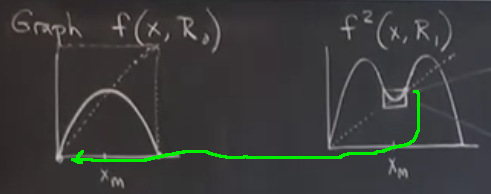
Bu grafikte sağdaki grafiğin küçük kutunun sağ üst noktası soldaki grafiğin orijindeki noktasına tekabül eder, ve sağdaki küçük kare soldaki büyük kareye tekabül eder. Ve eğer sadece bu iki kutunun içinde olanlara bakarsak, mesela küçük kutu içindeki eğriye bakalım, görüntüyü büyütelim,

göreceğimiz eğri bize üstteki sol grafikteki eğriyi çağrıştırmalı, sadece ters halde ve daha küçük tabii. Yani $f^2(x,R_1)$ ile $f(x,R_0)$ aynı yerel dinamiklere sahip sadece daha küçültülmüş ve ters çevrilmiş halde. Burada aynı yerel dinamiklere sahip derken mesela her iki kutu içindeki bölgelerde örümcek ağı diyagramı çizsen aynı şekilde davranacaklarını görürdüm. Bir sonraki fikre ilham veren sezgisel anlayış bu.

Bu arada üstte anlattığımız gayet gevşek, hafif belirsiz bir fikrin bir hesabın temeli olabileceği inanılmaz geliyor, çünkü bir anlamda çocukça bir gözlem gibi sanki, fakat mesela Güney Amerika kıtasının doğu tarafının Afrika kıtasının batı tarafına uyduğu gözlemi de böyle bir çocukça bir gözlemdi, fakat bu gözlemin çok önemli olduğu ortaya çıktı, çünkü bu gözlem kıtaların tek kitadan geldiği, bazılarının diğerlerinden ayrılarak parçaların başka yerlere sürüklendiği (continential drift) teorisine önemli bir destek sağladı. O zaman da bazıları dedi ki "olur mu yahu, şaka gibi bir şey", vs. Fakat o küçük kutudaki ölçeklenmiş ters duran eğri hakikaten o büyük olanla aynı. Periyot katlanmaları ardından gelen kaosun başlangıcını anlamaktaki çok derin bir gözlem bu.

Şimdi resimler yerine cebirsel olarak süreci tarif edelim, küçülme ve terse dönme ile ne demek istediğimi daha net şekilde anlatayım. Resme bakarsak herşey maksimum $x_m$ etrafında şekilleniyor, bu biraz rahatımızı bozan bir şey, maksimum alıp orijine kaydırırsam isim daha rahatlaşabilir, cebir daha temiz hale gelir. Esas ilgilendiğimiz aslında köşegendeki kutunun sağ üstündeki nokta, onu hem yatay hem de dikey eksenlerde kaydırak istiyoruz. Bu arada dikey eksen $y$ tam $y$ değil, o sadece bir sonraki $x$, o sebeple $x_m$'i çıkartınca onu hem şu andaki $x$ hem de gelecekteki $x$'ten çıkarmamız gerekiyor. Yani $x_m$'i $x$ ve $f$'den çıkartıyoruz. Önce $x_m$ sonra $f$ hesabı, ardından $r$ çıkartımı. Bu iki çıkartmayı yapınca alt sağdaki resmi elde ederiz,

Şimdi üstteki sağdaki grafiği $\alpha$ diyeceğimiz bir tek sayı ile ölçekliyoruz, $\alpha \approx -2.5$. Bu bize baştaki (üst soldaki) resmin aynısını veriyor.

Bunu formüllere çevirelim şimdi. Resme göre

$$ f(x, R_0) \approx \alpha f^2(\frac{x}{\alpha}, R_1) \qquad (2)$$

Yani $\alpha$'lar hem yatay hem dikey ölçeklenmeyi hallediyorlar.

Formülü uyguladık, aynı şekli elde ettik. Peki üst sağdaki sonuca (resim, formül) aynı formülü bir daha uygularsak ne olur? Hala aynı şeyi elde etmem lazım değil mi? Yani,

$$ \approx \alpha^2 f^4(\frac{x}{\alpha^2}, R_2) $$

Formülü ardı ardına uygulayabiliyoruz, genel formül olarak

$$ \approx \alpha^{n} f^{2^n}(\frac{x}{\alpha^{n}}, R_n) $$

Sözel olarak "N kere tekrar normalize ettiğimizi" söylüyoruz.

Bu arada eğer tarif edilenlerin biraz soyutlaşmaya başladığını düşünüyorsanız, tüm bunların çok basit hesapsal karşılığının olduğunu unutmayalım. Mesela bir lojistik haritayı alıyorum, ki bu $f$, bir karesel harita fonksiyonu, $R_0$'in ne olduğunu biliyoruz / onu hesaplayabiliyoruz çünkü nerede süperstabillik varsa orası, $1+\sqrt{5}$ galiba [bunu ödev olarak vermiştim değil mi diyor soruyor öğrencilere, cevap evet]. Bu değerleri $f$'ye geçiyoruz, bir sonraki değer geliyor, orada $f^2$ için aynı şekilde $R_1$ bulunur, $\alpha$ vs ile onu hesaplarız. Her iki fonksiyonun üstüste olduğunu görürüz. Öyle mistik bir işlemden bahsetmiyoruz. Hesap çizelgesinde (spreadsheet) ile bile gösterilebilir.

Feigenbaum'un üstteki hesabın limitine baktı, yani

$$ \lim_{n \to \infty} \alpha^n f^{2^n}(\frac{x}{\alpha^{n}}, R_n) = g_0(x) \qquad (1) $$

Ve bu limitin yakınsadığını gördü, yani limit mevcuttu. Yakınsama $g_0(x)$ diye tanımladığı bir nesneydi. Peki bu nesne neydi? İşte az önce gördüğümüz ters paraboldu, diğerlerinde olduğu gibi süperstabil bir sabit noktası olan bir fonksiyondu. Bu süperstabil bir sabit noktası olan evrensel bir fonksiyondu. Ama dikkat, bu durum eğer $\alpha$ doğru seçilirse ortaya çıkıyordu, yani her $\alpha$ için üstteki ardı ardına, bir sonraki noktanın özyineli hesaplanması yakınsama yaratmıyor. Spesifik olarak $\alpha = -2.5029..$ olmalı, incir ağaçı grafiğinde görülebilecek bir durum.

Evrensel derken limit fonksiyonunun başlangıç fonksiyonünden neredeyse tam bağımsız olmasından bahsediyorum. $f$ ile başladık, ki ona lojistik fonksiyon dedik, ama illa böyle olması gerekmiyordu. Tek hörgoçlu pürüzsüz maksimumu olan başka bir fonksiyon da olabilirdi. Mesela sinüs haritası ile başlayabilirdim, üstteki özyineli çağrıları yapabilirdim, aynı $\alpha$ ortaya çıkar, ve yine aynı limit fonksiyonu $g_0$ ortaya çıkar.

Bu olasılık teorisi dersi almış olanlarınıza Merkezi Limit Teorisi'ni hatırlatıyor olabilir. Bu teoride bilindiği gibi rasgele değişkenler birbiriyle ardı ardına toplanır, ve ortaya çıkan dağılıma bakılır. Eğer başlangıçtaki rasgele değişkenlerin sonlu ortalama ve varyansı var ise, ve belli bazı şartlarda ve cebirsel durumda ortaya çıkan limitteki dağılım [fonksiyonu] her zaman Gaussian [Normal] dağılımdır. Bu durum başlangıçtaki rasgele değişkenlerin dağılımı ne olursa olsun aynıdır, Bernoulli, Birörnek (Üniform), vs. Bu tür argümanın ilk örneklerinden biri MLT'dir herhalde.

Bu arada MLT'yi tekrar normalizasyon ile ispat etmek mümkün. İstatistikçiler, olasılık teorisyenleri çoğunlukla bu yöntemi takip etmez ama MLT üstte gördüğümü türden tekrar normalizasyon prosedürünün bir özel durumudur.

Soru

$\alpha$'yi doğru seçmekten bahsettiniz, bu seçim $f$'den bağımsız mı yapılıyor?

Cevap

Şimdilik söyleyeceğim $\alpha$ sayısal olarak seçiliyor, ve süreci yakınsamaya götürecek şekilde seçiliyor. Sonradan $\alpha$'yi analitik olarak ve evrensel bir fonksiyonu baz alarak hesaplayan bir formül göstereceğim; biraz sabır, herşey birbiriyle ilginç bir şekilde bağlanıyor. Şu anda $\alpha$'nin ne olduğunu bilmiyoruz.

Soru

Bu $\alpha$ niye ilk başta bahsedilen $\alpha$ ile aynı?

Cevap

Aynı $\alpha$ tabii, doğru. Niye? Öyle olması lazım, düşünelim, özyineli şekilde çağrı yapıyoruz, $R_n$ ile kaydırıyoruz, burada yaptığımız incir ağaçında ileri doğru adım atmak. $R_0$'da başladık, $R_1$'e geldik, vs. Bu şekilde sağa doğru, kaosa doğru adım adım ilerliyoruz, ve ilk başta $\alpha$'yi nasıl tanımladığımızı hatırlayalım, bu parametre dallanmayı, maksimuma yaklaştığımızda $x$ bağlamında ölçeklenmeyi kontrol ediyordu. O zaman en son yaptığımız özyinelemeye dönelim şimdi, hep maksimuma yakın yere bakıyoruz, ilk resimde tepe noktası, ikincide pencere içi alt nokta, pencere dışı sol tepe ya da sağ tepeye bakmadım. İşte incir ağaçı ölçeklemesinden bahsederken yaptığım işin aynısını yapıyorum, maksimum noktanın ve etrafının bakış açısından olanlara bakıyorum. Pencereler de zaten $x$ bağlamında ölçeklenmeyi kontrol ediyorlar.

Soru

$\alpha$ köşegen çizginin eğriyi kesmesiyle ortaya çıkmıyor mu / o yer değil mi?

Cevap

Tabii doğru, çünkü bu kesişme kutunun büyüklüğünü kontrol ediyor. Evet, o şekilde bakabilirsiniz. Limite giderken işleyecek doğru bir $\alpha$ seçmek lazım.. ilk birkaç özyinelemede o kutuların büyüklüğüne bakarak $\alpha$'nin yaklaşık büyüklüğünü tartabilirsiniz.. Evet. Sonuşurda ise arda arda gelen kutuların büyüklüğünün oranlarına bakıyoruz aslında.. Evet. Güzel gözlem.

Şimdi ilerleyelim. Daha işin başındayız, ısınıyoruz sadece! [Gülüyor]. Şimdiye kadar yaptığımız neydi? Süperstabil sabit nokta olarak evrensel bir fonksiyonumuz var, ama hala onun neye benzediğini bilmiyoruz, kabaca ters dönmüş bir parabola benziyor dedik, ama hikayenin tamamı daha çetrefil, çünkü o görüntü yerel bağlamda, maksimumun yakınında geçerli sadece. Eğer daha uzak noktalarda neye benzediğini bulmak istiyorsak daha derin düşünmemiz lazım. Diğer yandan şimdiye kadar süperstabil sabit noktalara sabitlendik, kafiyeli olsun diye söylemiyorum tabii, yanlış anlaşılmasın [öğrenciler gülüyor]. Ama süperstabil sabit noktalar konusunu geri bırakıp diğer nesneler hakkında konuşmaya başlamadan önce, süperstabil 2-çevrim, vs gibi, bir konuyu fark etmemiz iyi olur; [bir üstteki] geliştirdiğimiz bu resim bize evrenselliğin nereden geldiği hakkında güzel bir sezgi kazandırdı, sezgi şu soruyla alakalı: sonuç niye $f$'den bağımsız? Neredeyse tamamen bağımsız demek daha doğru tabii, çünkü kesin bağımsızlık yok, niye böyle olduğunu birazdan göreceğiz, ama evrenselliğin nereden geldiğini şimdi daha iyi görebileceğiz.

Limit fonksiyon neye bağlıdır? Bu bizi cevaba götürüyor; limit fonksiyonu $g_0(x)$ evrenseldir, çünkü davranışı başlangıç maksimum $x_m$ yakınındaki fonksiyon $f$'e bağlıdır. Niye böyle söyledim? Neler olduğunu düşünelim şimdi. Üstteki resim soldaki figure bakarsak onun maksimuna bakarak başladık (ki bu noktayı orijine tercüme etmiştik hatırlarsak), ardından bir özyineleme yaptık, ortadaki figürdeki daha ufak kutuyu elde ettik, devam ettik, hala bir önceki maksimumun olduğu noktaya odaklanıyoruz, ve $n \to \infty$ iken limiti alınca, belki (1) formülüne bakarak bunu daha iyi anlarız, $\frac{x}{\alpha^{n}}$ kısmına odaklanırsak, $n$ büyürken ne olacaktır? Yaptığımız sanki bir mikroskop alıp $x=0$'a yakın yerleri büyüterek oraya bakmaktır değil mi? Orada ardı ardına daha ufak, daha ufak kutular yaratıyoruz, ki buraları maksimumun yeni versiyonları.

Yani yerel davranışa odaklanıyoruz ve bunu sonsuz küçük bir bölgede, maksimumun yakınında yapıyoruz, bunu $\frac{x}{\alpha^{n}}$ özyinelemeyi işleterek başarıyoruz. O zaman düşünürsek hesapsal olarak bizim tek ilgilendiğimiz ilk resimdeki orijin etrafında ufak bir bölgede olanlar. $f$'in daha uzak yerlerde yaptığı hakkında tüm bilgiyi kaybediyoruz, $\frac{x}{\alpha^{n}}$ operasyonu sebebiyle sadece maksimum ve onun çok yakınındaki bölgeyi görüyoruz. Bu bize bir şeyler söylüyor aslında, söylediği maksimumun kendisinin doğasının önemli olduğu, diğer hiçbir şeyin önemi yok. Doğası derken mesela maksimum karesel mi? Yani oraya bir Taylor serisi koysam bu seride karesel bir terim olacak mıdır? Bu, maksimumun mesela 4. derece bir polinomun olduğu bir durumdan niceliksel olarak çok farklı olurdu. Ya da keskin kenarlara sahip olacak bir mutlak değer fonksiyonunun olacağı bir durumdan... Bu tür farklar üstteki metotla yakalanabilecek şeyler, fizikçiler maksimumda neler olduğuna bağlı olarak olabilecek bu değişik durumları "farklı evrensellik sınıfları" altında inceliyorlar.

Olan şu, $f$'nin global nitelikleri bu analizde yokoluyor, tek ayakta kalan maksimumun derecesi. Yani daha önce $f$'den bağımsız dediğimde söylemek istediğim "karesel maksimumu olan $f$ ailesi içinde". Yani mesela 4. derece bir $f$ için farklı bir $g_0(x)$ vardır, 6. derece için farklı, vs. Genelde olan elde bir karesel maksimumun olması, ve bizim ele aldığımız durum bu. Feignbaum'un analizinin geri kalanı ile devam edelim; şimdiye kadar süperstabil sabit noktalardan bahsettik. Ya elimizde süperstabil bir 2-çevrim olsaydı? O zaman farklı evrensel fonksiyonlar elde edebilirdik.

Tüm bunlar bir zirveye doğru gidiyor bu arada, merak etmeyin.

Neyse diğer evrensel fonksiyonları elde etmek için, ki onlara $g_0(x)$ yerine $g_i(x)$ diyelim, $f(x,R_i)$ ile başlarız (daha önce $f(x,R_0)$ ile başlamıştık), yani süperstabil $2^i$-çevrime sahip olan bir $f$ ile başlıyoruz. Bu noktadan sonra süperstabil $2^i$-çevrime sahip fonksiyonların dünyasındayız, ve daha önce işlettiğimiz süreci tekrarlıyoruz, limitleyen fonksiyon $g_i(x)$'i bulmaya uğraşıyoruz,

$$ g_i(x) = \lim_{n \to \infty} \alpha^n f^{2^n} (\frac{x}{\alpha^n}, R_{n+i}) $$

Fakat bu $i$'lerin içinde öyle bir tanesi var ki ötekilerinden daha iyi. Bunu şöyle düşünebiliriz, incir ağacı içinde ilerliyoruz, süperstabil noktada dallanma, süperstabil 2-çevrimde tekrar dallanma, 4-çevrim, vs.. Burada odaklanabileceğimiz gayet doğal bir $i$ seçimi olduğunu görebiliyor muyuz? Bakmak istediğim kaosun başlayacağı yer.. o zaman $ı = \infty$'a bakmam gerekir. Bazilariniz diyebilir ki "ama $\infty$, yani sonsuzluk bir sayı değil". Ama bunun ne kadar iyi işlediğini görmemiz gerekir.. (2) formülüne bakalım mesela, ikinci döngü / kat almadan sonra $\alpha$ ile ölçekleyere tekrar normalizasyon yaptığımda, $R$'yi de arttırmam gerekiyor. Değil mi? $R_0$'dan $R_1$'e, oradan $R_2$'ye, vs.. Sonsuzluğun güzel tarafı sonsuzluk + 1 hala sonsuzluk. Orada $R$ kaydırma yapılmasına gerek yok. Eğer $R_\infty$ üzerinde isem bir sonraki döngü beni yine $R_\infty$'a getirir. Evet biliyorum çılgınca ve havalı bir şey [gülüşmeler].

O zaman $R_\infty$'da olduğumüz durumu daha yakından inceleyelim. Süperstabil $2^i$-çevrimin olduğu durum yerine süperstabil $2^\infty$-çevrimin olduğu duruma bakalım, ki bu an tam kaosun başladığı nokta. En iyi ve en ilginç olan örnek bu, $R = R\infty$ olduğu durum. Bu durumda

$$ f(x,R_\infty) \approx \alpha f^2(\frac{x}{\alpha}, R_\infty) $$

olacaktır çünkü $R$'nin kaydırılması gerekmiyor, yaklaşık eşitliğin sağında ve solunda $R$ indisi aynı (sonsuzluk). Bu noktada ne olduğuna daha yakından bakabiliriz artık, sonuçta kaosun çıkış ani, o ana giderken olanlar bizi ilgilendiren kavramlar.

Tekrar normalizasyon işlemini döngüde ardı ardına işletince ne olur? $g_i$ yerine $g_\infty$ gibi bir nesne elde ederiz. Gerçi buna çoğunlukla $g_\infty$ denmez, $g_\infty$'in limitleyen fonksiyonuna $g(x)$ denir, ve şu denklemi tatmin eder, $g(x)$ ile başlayıp tekrar normalizasyonu uygulayınca,

$$ g(x) = \alpha g^2(\frac{x}{\alpha}) $$

elde edilir (alt indis değerini vermedim çünkü $R_\infty$'da olduğunu biliyorum). Bu denklem doğrudur - bu fonksiyon tekrar normalizasyonu kendisidir, $R$'yi kaydırmadık.

Feigenbaum'un bulduğu üstteki formüle "fonksiyonel denklem (functional equation)" adı veriliyor. Bu tür denklemleri derslerde daha önce görmemiş olabilirsiniz, lineer denklemleri gördünüz, cebirsel denklemleri gördünüz, lineer diferansiyel denklemler, belki entegral denklemleri bile gördünüz, ama fonksiyonel büyük bir ihtimalle hayır. Fonksiyonel denklemler bir fonksiyonu yine kendisini kullanarak temsil eder, üstteki durumda ikinci döngüdeki hali üzerinden ama bağlantı fonksiyonun üzerindeki farklı bir işlem üzerinden de olabilirdi.

İşte $g$'nin fonksiyonel denklemi bu, denklemdek $\alpha$ var bu değer bir anlamda, tam anlamıyla olmasa da, bir özdeğer görevini görüyor sanki.

Üstteki tanıma ek olarak bazı sınır şartları tanımlamamız gerekiyor, üstteki tanım $g$'nin nihai tanımı için yeterli değil. Eğer $g$'yi yerel bağlamda zihnimizde canlandırmak istiyorsak onu $R_\infty$'da tanımlı lojistik harita olara düşünebiliriz. Kabaca spesifik bir $R$ değerindeki su

resme benziyor. Yerel olarak $g$ böyle, ama hatırlarsak $x$ eksenini öyle seçtik ki maksimum sıfır noktasında, o zaman bir sınır, ya da yan şart tanımlamalıyız öyle ki $g'(0)=0$, yani maksimumda eğim sıfır (maksimumu orijinde olacak şekilde daha önce kaydırmış olduğumuzu farzederek). Ayrıca $g$'nin karesel maksimumu olduğunu şart koymak / zorlamak istiyoruz, yani 4. vs. derece değil, karesel, o zaman üstteki fonksiyonelin çözümünü bulmak için karesel aile içinde arama yapacağız.

Bu arada formülleri biraz temizlemek için bir ölçek dahil etmek mümkün, yani mesela baktığımız birim santimetre mi.. kulağa acaip geliyor ama demek istediğim, üstteki resimdeki tepe noktası ile yatay eksen arasındaki yükseklik nedir? O sayı ne anlama geliyor? O sayıyı genelleme kabiliyetini kaybetmeden [ölçekleme ile] 1 yapabilirim. Bu nasıl oluyor? Çünkü eğer $g(x)$ tüm yan şartları tatmin ediyor hem de fonksiyonel denkleme çözüm sağlıyor ise, herhangi bir $\mu$ için $\mu g(\frac{x}{\mu})$ da bir çözümdür, yerine geçirerek kontrol edebilirsiniz. $\mu$ için bir sayı seçin, ve bakın. Bunun yaptığı $\mu$ kadar $x$'in ölçeğini değiştirmek. O yüzden dedim ki genellikte kayıp olmadan onu öyle seçebiliriz ki ölçek 1'e eşit olur.

Neyse, işte elde bazı şartlar var, şimdi fonksiyonel denklemi çözmek istiyorum, ama bunu nasıl yapacağımızı bilmiyoruz şu anda.. Üniversitelerde fonksiyonel denklem çözmeyi öğreten dersler öğretilmiyor, biraz bir egzotik konu bu, çok fazla ortaya çıkan bir şey değil. Onlar hakkında doğru dürüst kitap bile bulmak zordur. Feigenbaum'da becerikli bir bilimcinin yapacağını yaptı, onu güç serileri ile çözmeye uğraştı. Öyle değil mi, başka hiçbir şey işlemeyince güç serisini pat diye koyarız oraya, ve ise koyuluruz. Şunu denkleme sokarız,

$$ g(x) = 1 + c_2 x^2 + c_4 x^4 + ... \qquad (3) $$

Seri 1 ile başlıyor çünkü $g(0)=1$ olduğunu biliyoruz. Tüm bu şeyler [döngüler sonucunda ortaya çıkan fonksiyonlardan bahsediyor] tersine dönmüş parabola benziyorlar, onların çift olacağını göstermek bile mümkün olabilir zannediyorum, o sebeple üstte çift üstel dereceler kullandım. Yakınsayan güç serisi olan analitik bir fonksiyon kurmaya uğraştım yani, ki bununla $g$'yi temsil edebileceğimi tahmin ettim. Şimdi üstteki fonsiyonu $g$ yerine koyabilirim, açılımı yaptıktan sonra $x$'in belli derecelerdeki katsayılarını gruplamaya uğraşırım, vs. Bunu yaptıktan sonra Feigenbaum $c_2 = -1.527...$, $c_4 = 0.1048..$ buldu.

Burada dikkatimizi çeken bir şey var mı? Eğer $x=0$ yerine koysak bu bize ilginç bir bilgi kazandırır mı? Kazandırır değil mi?

Pardon sıramı karıştırdım biraz.. $c$ değerlerinden önce $\alpha$'yi bulmam lazım. Yan şartları tanımladıktan sonra $g(0)$ nedir? Ölçeklemeyi öyle seçeriz ki $g(0)=1$ yapabiliriz dedik.

$$ g(0) = 1 = \alpha g(g(0))$$

Ama foknsiyonel dekleme göre $g(0)$ aynı zamanda üstteki eşitliğin en sağ tarafına da eşit olmalı. Şimdi $g(0)=1$'i eşitliğin en sağınde yerine koyalım,

$$ g(0) = 1 = \alpha g(1)$$

Bu bana ne söylüyor? $\alpha$'yi $g$'ler üzerinden temsil etmemi sağlayacak bir formüle erişmedim mi? Tekrar düzenlersek,

$$ \alpha = \frac{1}{g(1)}$$

Vay canına. Ortaya çıktı ki $\alpha$ ve $g$ birbirinden bağımsız değil. $\alpha$, $g$'ye, o ana fonksiyona bağımlı. Vay vay.. şimdi geriye dönelim, (3)'te tanımlı $g$'yi yerine koyabiliriz şimdi, ve bir üstteki tutarlılık şartını da kullanınca, tüm bunlarla Feigenbaum'un bulduğu $c_2$, $c_4$ sayılarına erişmek mümkün. Ve en son olarak $x=1$'i (3) içine koyunca ve bir üstteki şartla beraber $\alpha$'yi hesaplamak mümkün, işte bu hesaptan $\alpha = -2.50..$ gelecek.

Tekrar düzenleme argümanının başlangıcı burası. Daha işimiz bitmedi, çünkü eksik olan birşey hala var. Şimdiye kadar açıkladığımız periyot katlanmasında niye evrensellik olduğu, $g$'yi hesapladık, $\alpha$'yi hesapladık, ama hala $\delta$'yi hesaplamadık, hatırlarsak $4.66..$ diye giden sayı. Nerede bu $\delta$? Şimdiye kadar kurduğumuz formüllerin hiçbirinde mevcut değildi. Bir sonraki derste işte bu $\delta$'yi bulacağız, bu tekrar normalizasyon argümanının son noktasını koyacak.