Ders 20

[Dersin başında [3] hocanın yaptığı demo atlandı, periyot katlanması, lojistik eşlemeyi gösteren programlar sundu]

Kaosun evrensel mekanizmasına geldik. Bu kısım tüm dersteki en zor kısımlardan biri olacak, o yüzden zihnimizi açık tutalım, performansı arttıracak bir düğme varsa ona basalım :) Çok abartmayım tabii, sadece bu ve takip eden birkaç dersin soyutluk ve zorluk seviyesi diğer bölümlere nazaran biraz daha yukarıda. Ama bu zorluk çekmeye bence değer çünkü konumuzun entellektüel kazancı açısından vardığı en yüksek nokta burası.

Anlatacaklarım kitabımın 10.6, 10.7 bölümünden, Feigenbaum adlı bilimcinin 1978 yılında yayınlanan araştırmasını [1] merkez alıyoruz. Daha rahat okunan bir makalesi daha var [2], isteyen onu okuyabilir. Feigenbaum ilginç bir karakter, hikayesinin anlatmak faydalı olabilir... Ayrıca fotoğrafına bakın, Feigenbaum film yıldızı gibi bir tiptir, gençliğinde onu konferanslarda gördüğümde en azından öyleydi. Beethoven'in gençliğine benziyor bir bakıma, karışmış çılgın bilimci saçları, gözlerde odaklı / zeki bir bakış, vs.. Herneyse, tam bir dahi goruntusu.. Hikayenin geçtiği sırada Los Alamos labaraturında çalışıyor, Los Alamos bilindiği gibi tarihte nükleer bomba üzerinde çalışan Manhattan projesiyle anilir, orada pek cok zeki bilimci calisir, burada bile Feigenbaum'a herkes en zekilerden olarak bakıliyor. Dusunun!

Fakat Feigenbaum kariyerinin bu noktasında büyük bir problem daha çözmemiş, en azından yetenekleri çapında büyük bir problem çözmemiş. Onun için rahatsız edici bir durumda bu herhalde, çok zeki ama daha bilim literatüründe iz bırakmamış. Gleick'in kitabına göre, Feigenbaum da bu noktada üzerinde çalışabileceği "büyük" bir şey aramaya başladı. Türbülans konusu ile ilgileniyordu, daha da ilgisini çeken genel bir soruydu, "doğada kaos nereden geliyor, sebebi nedir"? Bu fenomenlerde düzensizliğe sebep olan ana faktörleri merak ediyordu. Niye bazı şeyler düzenlidir, diğerleri değildir? Bulutlara bakıyordu mesela, burgaçlara (eddy).. suyun bir delikten akarken oluşan dönüşüyle ilgileniyordu.. Bu fenomenler onu bir şekilde lojistik haritaları düşünmeye itti, lojistik haritanın bu fenomenleri daha basit olarak temsil edebilecek bir modelde kullanabileceğini düşünmeye başladı. LH sistemlerin düzenden düzensizliğe, ve nihai olarak kaosa varışını basit olarak yakalayabilirdi belki. Derin bir araştırmaya başladı, daha önce söylediğim gibi lojistik harita 60'lı yıllardan beri araştırılıyor, ama Feigenbaum LM hakkında çok daha derin bazı sonuçlara ulaştı. Gerçi bulgularını yayınladıktan sonra uzun süre kimse ne anlattığını anlamadı.

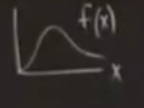
Feigenbaum pek çok tek-hörgoçlu [devede olduğu gibi] ya da tek-doruklu (unimodal) haritada periyot katlanmalarına (period doubling) baktı, yani pürüzsüz durumda tek maksimumu olan şeylere. Mesela $x_{n+1} = r f(x_n)$ böyledir

İlla parabol olması şart değil, tek-doruklu olan herhangi bir başka şekil de olabilir. Feigenbaum bu haritalarla alakalı $f(x)$'in formundan bağımsız olan ama genelde geçerli olan çok net niceliksel kanunlar buldu. Bu çok ilginç aslında, girdimiz ne? Tek doruklu pürüzsüz herhangi bir harita. Bu girdiyi kullanarak bazı sonuçlara erisebiliyoruz, $f$'e bağımlı olmayan çok net bazı sayılar üretebiliyoruz. Bu gizemli bir durumdu fakat Feigenbaum bu gizemli durumu istatistiki fiziğe bağlantılar yaparak açıkladı. Bunu istatistiki fizikçilerin "evrensel üsteller (üniversal exponents)" dediği kavramla bağlantı kurarak yaptı. Bu üstellerin 2. derece faz geçişlerinde ortaya çıktığı gözlemlenmişti, mıknatıslarda, süpersıvılarda, vs.

Bu istastiki fizikteki bilinen önemli hikayelerden biri; belki hikayeyi biraz anlatsam şimdi iyi olur, çünkü kısmen bu hikaye Cornell'le [hocanın okulu] alakalı. Kimya departmanımızda çalışan Ben Wittem var, eski hocalardan Michael Fisher var, Ken Wilson var ki bu konuyla alakalı bir buluşla Nobel ödülü kazandı. Hepsi faz geçişleriyle ilgileniyordu. Deneyciler buldu ki faz geçiş anında çoğunlukla üstel kanunlar (power law) ortaya çıkıyor, manyetikleşme derecesinde mesela ki bu derece manyetik alandaki okların ne kadar aynı yönü gösterdiği ölçer, bu manyetikleşme, $m$ diyelim, ısı $T$ ile ne kadar alakalıdır? Öyle bir kritik ısı noktası var ki o geçilirse mıknatısa daha fazla verilen ısı okları bir süre sonra bozar, yönler karmakarışık hale gelir, mıktanış manyetik özelliğini kaybeder.

Araştırmacıların merak ettiği kritik ısıdan ne kadar uzak olduğumuzun manyetikleşmeye nasıl etki ettiği. Bulgu manyetikleşmenin $T \sim |T-T_k|^\beta$ şeklinde büyüdüğü, yani kritik noktaya olan uzaklığın bir katına oranlı olarak (üstel kanun burada). Resimde görülen üstel karekök (yani üstel 1/2) fonksiyonu, ama başka bir üstel de olabiliyor. Bu $\beta$'ları ölçtü araştırmacılar, ve ilginç olan kısım, üstte baktığımız mıknatıs, ama başka bir sürece bakıyor olabilirdik mesela süpersıvılar, ya da başka bir şey, ve belli bazı şartlar altında tamamen farklı deneylerde aynı $\beta$'nin ortaya çıktığı görülüyordu. Bu büyük bir şoktu. Bir tarafta klasik bir olay var, diğer tarafta kuantum mekanik bir olay var, ama aynı $\beta$'yi gösteriyorlar.

Kritik fenomenler hakkında ders almış olanlar bu bulguyu duymuştur, müthiş büyük bir haberdi. Bu aynılığın nereden geldiği sonradan keşfedildi, ve keşfi yapanlar tekrar normalizasyon grubu buluşunu yaptı, Ken Wilson'a Nobel'ini kazandıran bu işte, pek çok diğer kişinin de o buluşta payı var tabii ki. Feigenbaum tekrar normalizasyon fikirlerini kullanarak birazdan göreceğimiz gözlemleri yaptı, fizikçilerin tekrar normalizasyonu kullanarak kritik fiziksel olaylardaki evrenselliği açıklayabilmesi gibi o da incelediği olaylardaki evrenselliğe açıklik getirdi.

Bu bağlantı pek çok kişinin dikkatini çekti. Bakıyoruz Nobel ödülü kazandıran saygı duyulan bir fizik dalında kullanılan teknik, o ana kadar marjinal, köşede kalmış görülen bir dal Kaos'ta faydalı oluyor. Kaos bu noktada bir alan bile sayılmazdı, ciddiye alınmayan bir sürü kişinin gezindiği bir alandı. Feigenbaum daha bilinen birisi değil, Ed Lorenz var meteoroloji alanında hava durumunu inceliyor herkes ona senin modelin yanlış diyor, hava böyle işlemez. Yani gerçekten durum böyleydi, Kaos kimsenin ciddiye almadığı böyle kenarda kalmış bir alandı.

Önemli bir nokta Feigenbaum'un bulduklarının test edilebilir hesaplar, tahminler yapabildiğidir. Tabii her kaotik sistemin periyot katlanma senaryosunu takip ettiğini söylemiyoruz, ama ediyorsa, o zaman Feigenbaum bu sistemler hakkında çok net tahminler üretebildi, bu tahminler deneylerle doğrulandı ve bu sistemler daha önce belirttiğimiz gibi kimi kimya kimi fizik gibi doğabilimin çok farklı alanlarındandı.

Uygulamaları daha da ileri taşıyanlar oldu mesela kalp hücreleri üzerinde, ama burada veriler ve bakılan sistem pek net değildi, kimisi daha da ileri gitti, teknikleri borsaya uygulamaya çalışanlar oldu. Bu alanda çok uçuk bazı iddialar yapanlar oldu, bu arkadaşların çok iyi bilim yaptığı söylenemez, ama daha önce belirttiğimiz kontrollü (kaotik olsada) sistemlerde çok iyi sonuçlar ortaya çıktı.

Şimdi evrensel ile ne demek istediğimi anlatmaya çalışayım. Lojistik harita yerine başka bir haritaya bakalim, mesela $f(x) = r \sin \pi x$ haritası, ki daha önce olduğu gibi $0 < x < 1$, sinus egrisinin bir bolumu bu, maksimumu $x=1/2$ noktasindaki $r$. Hatirlarsak lojistik harita icin maksimum $r/4$ noktasindaydi. Eger karsilastirma yapacaksak bu haritayi 4 ile carpip olceklememiz gerekirdi.

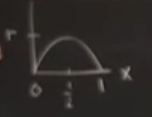
Herneyse, bunu inceleyebilirsiniz, bu biraz rahatsız edici bir iş olabilir, baktığımız şey lojistik haritadan çok farklı, $\sin$ fonksiyonunun McLauren serisinde $x$'in tüm tek sayılı üstelleri vardır.. $x,x^3,x^5,..$ gibi. Bu bir aşkın (transcendental) fonksiyon yani, öteki taraftaki $x^2$ gibi basit bir gayrı-lineerlik değil. Fakat eğer bu fonksiyonun yörünge diyagramını çizsek öteki sistemin yörünge diyagramına benzediğini görürdük.

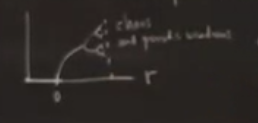
$r$ fonksiyonu bazlı grafiği çizince benzer bir hikaye göreceğiz, belli bir süre gidiş sıfır seviyesinde, sonra dallanma, periyot katlanması, sonra o katlananların katlanması, bu sürekli katlanma devam ederek kaosa gidiş. Periyodik pencerelerin mevcudiyeti.. Tabii ki önemli olayların olduğu $r$'ler bu sefer değişik olacak, çünkü farklı bir fonksiyona bakıyoruz.

Bütün bunlar Feigenbaum'dan önce biliniyordu aslında. Periyot katlanıyor, vs. Feigenbaum'un ilgilendiği ve değişik olan o periyot katlanmasının detaylarıydı, onun nasıl basamaklama (cascade) halinde devam ettiği, bunun hangi dinamiklere bağlı olduğuydu. Spesifik $r_n$'ler tabii ki incelenen haritanın $f(x)$'ine bağlıydı, ya peki aradaki boşlukların oranı? Yani önceki derste yazdığım $\frac{r_n - r_{n-1}}{r_{n+1} - r_n}$ hesabı.. Kaosa yaklaşırken, yani $r_\infty$ olurken bu hesaba bakarsak, oranın bir sonlu sayıya yaklaştığını görürdük. Bu sayının daha önce gördüğümüz $\delta$ ismi verilen aynı sayı 4.6692 olduğunu görürdük. Birazdan Feigenbaum'dan bir paragraf okuyacağım, bu yorum çok hoşuma gidiyor.. Dediğıim gibi Feigenbaum bu $r_n$'ler ile yakından ilgilendi, onların bazılarını analitik olarak hesaplayabileceğimizden bahsetmiştik, ama Feigenbaum onların hepsini analitik olarak hesaplamak istiyordu. Aklına matematikteki "üreten fonksiyonlar" kavramını kullanmak geldi. Bu teoriyi önce hesapsal olarak test edeyim dedi, Los Alamos'ta tabii o zaman bile en iyi bilgisayarlar, süper bilgisayar vs var, gerçi Feigenbaum bilgisayarda çok usta sayılmazdı, ama bilimsel hesap makinasını iyi kullanıyordu ki bu aletler o zamana göre bile oldukca kuvvetli makinalardı [bunu ben de hatırlıyorum, HP bilimsel hesap makinaları mesela, programlanabilen makinalardı]. Feigenbaum hesap makinasını programlayıp bir sonraki $r_n$'nin nerede çıkacağını hesaplattırdı. İlk hesabıyla üstteki 4.6692 sayısını veren kuralı buldu, ama o dedi ki bu sayı nereden geliyor? Yani $\pi^2 / 6$'midir, vs? Başka bilinen nelere bağlıdır yani.. Diyor ki

"Bütün günümü 4.6692 sayısını bildiğim diğer matematiksel sabitlerle ilişkilendirmekte harcadım ($e$, $2^x$, vs). Bunların hiçbiri sonuç vermedi, tek elde ettiğim bu sayının artık zihnime kazınmış olması. [Sonra farkettim ki] benim üreten fonksiyon bazlı teorim $f(x)$'in gayrı-lineerliginin karesel olduğunu farz ediyor. Bu konuya olan ilgim azalmaya başladı. Ama sonra hesap makinasıyla $\sin$ bazlı harita için (üstteki) oranı hesaplattırdım, 4.6692 sayısı çıktı (bu sayıyı hemen tanıyor çünkü artık hafızasına kazınmış)".

Bu noktada Feigenbaum bilgisayarları daha iyi öğrenmeye karar verir, ve boşluk oranını envai türden problem için hesaplamaya başlar, ve aynı sayıyı bu problemlerde de aynen görür.

Sabiti teorik olarak açıklamaya gelelim. Bu sayı $r$ yönünde bir tür evrensel ölçeklemeyle alakalı. $x$ yönünde de bir evrensel ölçeklenme durumu var, ki Feigenbaum onu da keşfetti. Bununla ne demek istiyorum? Periyot pencerelerinde görülen ağaç kümesi hatırlarsak bazısı dikey yönde daha fazla yer kaplıyor, kimisi daha az yer kaplıyordu. Feigenbaum bu yer kaplama hakkında bir hesap yaratmaya uğraştı, o yöndeki ölçeklemeyi bulmaya çalıştı.

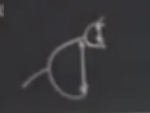
Yani üstteki resimde solda olan yüksekliğin sağda ve daha yukarıda olan yükseklik ile ilişkisi nedir? Ama $x$ yönündeki yüksekliğin o anda grafiğin hangi noktasında olduğumuz ile de bir ilişkisi var [yani iki ağaççık arasında bile bu değişim oranlara etki edebilir, bu sebeple bu faktörün orandan bir şekilde çıkartılması gerekir].

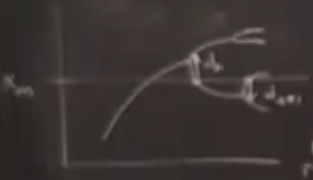
Periyot katlanmalarını gösteren ağacı tekrar çizelim; $x$'de lojistik harita için 1/2 seviyesinde bir çizgi olduğunu düşünebiliriz. Şimdi oran hesabı için $x$'leri ölçerken onları $x_m$'den başlayarak ölçüyoruz, $d_n$ diyelim. $x_m$ nereden geldi, bu maksimum, orada eğim sıfır, ayrıca orada her mümkün periyot için süperstabil noktalar ve çevrimler var, yani ağaç dalları muhakkak bir noktada $x_m$'i kesmek zorundalar, süperstabilliği ileride daha detaylı göreceğiz. Devam edelim, bu mesafeyi alıp ve bir sonraki $d_{n+1}$ ile beraber oran için kullanıyoruz. Feigenbaum'un ilgilendiği $d_n / d_{n+1}$ oranı, ve bunlara bakınca gördü ki $d_n$ her zaman $d_{n+1}$'den büyük ve her zaman ters işarete sahip. Ayrıca oran bugün $\alpha$ olarak isimlendirilen -2.5029'a yakınsıyor, bu sayı sinüs haritası, lojistik haritası, vs. benzer niteliklere sahip tüm haritalar için tıpatıp aynı. Anlamak istediğimiz $x$ yönündeki bu ölçekleme faktörü, aynı şekilde yatay yöndeki $\delta$'yi da anlamaya uğraşacağız.

Kaynaklar

[1] Feigenbaum, Quantitative universality for a class of nonlinear transformations, https://www.researchgate.net/publication/226628603_Quantitative_universality_for_a_class_of_nonlinear_transformations

[2] Feigenbaum, Universal Behavior in Nonlinear Systems, https://wwwusers.ts.infn.it/~milotti/Feigenbaum_1983.pdf

[3] Strogatz, Non-Linear Dynamics and Chaos Lecture 20, https://youtu.be/ol6aQcgohxI