Ders 18

Önceki derste Lorenz sistemi ve onun karmaşık dinamiğinden bahsettik. Ve nihayet [dersimizin ana teması kaosun merkezi olan] başlangıç noktasına olan hassas bağlantı kavramıyla tanıştık. Bu durumda birbirine yakın gidiş yolu yaklaşık olarak üstel hızda birbirlerinden ayrılıyordu, demiştik ki bu ayrışmanın hızı, $\lambda$, ki $e^{\lambda t}$ formülündeki $\lambda$ bu, "en büyük Lyapunov üsteli" idi, ya da ona kısaca "Lyapunov üsteli" diyorduk. Eğer Lyapunov üsteli pozitif ise bir üstel ayrışma vardı ve bu kaosun bir nevi imzası, onun olduğunu gösteren bir ipucu olarak görülebilirdi. Sonra Lyapunov üstelinin bize bir zaman skalası sağladığından bahsettik, bu skala $1/\lambda$ idi, bu skalaya Lyapunov zamanı, ya da "tahmin edilebilirlik ufku (predictability horizon)" adı vermiştik, bir kaotik sistemin ne yapacağını net olarak hesaplamak bu ufkun, rakamın birkaç katı ötesinde pek mümkün olmuyordu.

Bu derste kaos, garip çekici (strange attractor) gibi terimler hakkında daha net olmak istiyorum ve Lorenz'in makalesinde yaptığı çok akıllıca bir şeye dikkat çekmek istiyorum; onun bulduğu çekici sadece çok uzun bir limit çevrimi değildi. Bu uzun süre merak konusuydu, yani bu garip çekicinin gerçekten "garip" olduğuna emin miyiz? Belki de sadece çok büyük bir limit çevrimidir, eğer yeterince beklesek onun kendinin tekrarlamaya başlayacağını görürdük belki.. Lorenz'in bu konuda ortaya koyduğu kanıtı işleyeceğiz, tam formel bir ispat değil bu ama fikir verici, imalı bir kanıt.

Kaba hatlarla bazı tanımlar ortaya koyalım şimdi, kaba hatlarla diyorum çünkü bu tanımlar bir pür matematik dersinde olduğu gibi bir ispat için kullanılabilecek türden tanımlar değiller, daha çok kavramsal tanımlar, ki konunun geri kalanı anlamlı olsun.

Tanım: Kaos

Deterministik bir sistemde başlangıç şartlarına hassas bağlantısı olan uzun vadeli periyodik olmayan davranış.

Burada bir sürü jargon (terim) var. Periyodik olmayan en basiti, adı üstünde. Periyodik olmayan derken bunun çok basit türlerini kastetmiyoruz tabii, mesela bir denge noktası olmamalı, ki onun periyotu sıfır olurdu ve kağıt üzerinde "periyodik olmayan" gibi görülebilirdi, ama biz bu tür basit olanları kullanmayacağız. Periyodik olmayan derken bir denge noktasına düşmeyen ve periyodik olarak kendini tekrar etmeyen sistemlerle ilgileneceğiz.

Uzun vadeli davranış dedik, bazıları bunun kaos tanımının önemli bir parçası olduğu hakkında hemfikir olmayabilir, fakat özellikle kendi kendini besleyen kaostan bahsediyorum, ki bu tür kaos uzun vadede bile periyodik olmayan davranışta sergiliyor, geçici değil.

Determinism hiç gürültü, rasgelelik olmayan, rasgelelik içermeyen türden sistemler, öyle modeller ki eğer aynı başlangıç şartlarını kullanırsanız sistemi ileri doğru işletince her seferinde aynı sonucu alabilesiniz. Mevcut zaman geleceği tam olarak belirliyor. Tabii bu demektir ki eğer mükemmel bilgiye sahip olsaydık ileri doğru entegre ederek geleceği tahmin edebilirdik, fakat mükemmel bilgiye sahip değiliz ki bu daha önce bahsettiğimiz tahmin edilemezlikle alakalı.

Ve nihayet başlangıç şartlarına olan hassas bağlantı; dedik ki başlangıçta birbirine çok yakın iki gidiş yolu cebirsel olarak değil, mesela lineer, ya da $t$'nin üsteli bağlamında, ortalama olarak üstel olarak birbirlerinden ayrılıyorlar, ki bu hata büyümesinin patlama yapması demektir. Hatırlarsak daha önce torus üzerinde hemen hemen periyotluk (quasi-periodicity) kavramını görmüştük. O durumda da periyodik olmama, uzun vadelik, determinizm vardı, fakat kaos değildi çünkü başlangıç sonrası üstel ayrışma yoktu, ayrışma $t$'nin üsteliyle orantılıydı, hatta lineer idi. İşte bu sebeple hemen hemen periyodik olmama kaos değildir. Ayrıca pozitif Lyapunov üstelin olması başlangıç şartlarına olan hassas bağlantı var demenin farklı bir yoludur.

Sık kullandığımız bir diğer terim çekici. Bu arada bu terimlerin hakkında literatürde ortak bir konsensüs oluşmadı, farklı kitaplar, farklı hocalar terimleri biraz farklı şekilde kullanabilirler. Ama herhalde herkes bir çekicinin alttaki özelliklere sahip olduğunda hemfikir,

1) Değişmeyen bir küme ($A$'da başlarsanız $A$ içinde kalırsınız).

2) Açık küme başlangıç şartlarını çeker.

3) $A$'nin hiçbir muntazam altkümesi 1 ve 2'yi tatmin etmez (buna $A$'nin "minimal" olmasi da deniyor).

Kaos tarifi yapmıyoruz dikkat, hala çekici tarifi yapıyoruz.

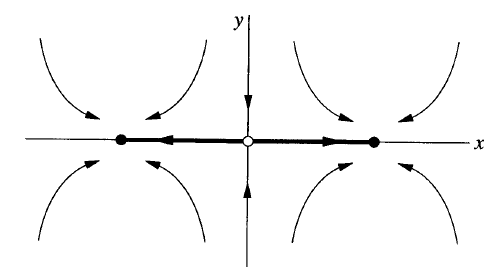
Diyelim ki alttaki gibi iki stabil noktalı, faz portresi alttaki gibi olan bir sistem var,

Herşey iki stabil noktalardan birine akıyor. X-ekseninde değişmezlik var, "herşey" dedim ama tabii y-ekseninde başlayan orijindeki eğer noktasına gidebilir. Soru şu, bu tür bir resimde çekici adayları hangileri? Ortadaki eğer noktası mesela, bu bir çekici mi? Listeden kontrol edelim, bir değişmez küme mi? Evet, eğer noktasından başlayan orada kalır. Bu nokta açık küme başlangıç şartlarını çeker mi? Hayır. Ne çeker? Y-ekseni üzerindeki noktalardan müteşekkil kapalı kümeyi çeker. Açık, kapalı derken neyden bahsediyoruz? Topolojiyi ya da analizi hatırlayalım, bir düzlemde ya da $\mathbb{R}^3$'te açık küme demek, eğer bir küme etrafında onu çevreleyen noktalar tanımlarsam bu noktalar küme dışına "taşar". Üstteki durumda bu normal çünkü baktığımız bir tek çizgi sadece (y-ekseni). Çizgi düzlemde açık küme değildir. Demek ki üstteki eğer noktası, orijin, bir çekici değil, 2. şartı ihlal ediyor.

Ya x-ekseni? Herşeyin aktığı noktaların hepsi x-ekseninde olduğuna göre bu bir çekici olabilir mi? Değişmeyen küme mi? Orada başlayınca orada kalınıyor mu? Evet. Açık küme başlangıç şartlarını çekiyor mu? Evet, $\mathbb{R}^2$'nin tamamını çekiyor. Düzlemde nerede olursanız olun x-eksenine gidersiniz, sonuşurda x-eksenine gidersiniz daha doğrusu. Ve tüm düzlem bir açık kümedir, düzlemdeki herhangi bir noktanın etrafında onu çevreleyen ufak bir açık disk çizilebilir, ve bu disk te düzlemin parçası olur. 2. tatmin edildi demektir.

Ya #3? X-ekseninin 1 ve 2'yi tatmin eden muntamam bir altkümesi var mıdır? İşte burada bir problem var, bir çekici içinde kendileri de çekici olan daha ufak nesneler barındırmamalıdır. Çekici olarak düşünülen şeyler eksen üzerindeki iki stabil nokta, esas çekiciler onlar, x-ekseni değil. X-ekseni gibi şeylere bir "çekici küme" deniyor ama bir çekici değil, çünkü bu küme minimal değil.

O zaman stabil noktalar çekici, listemizle kontrol edelim, orada başlayınca orada kalınır, 1 tamam. Açık küme başlangıç şartlarını çeker mi? Mesela sağdaki stabil nokta neyi, neleri çeker? Tüm düzlemin sağ yarısını, yani açık sağ düzlem (ki y-ekseni haricinde onun sağına kalan tüm noktalar) çekiliyor, bu noktalar açık bir küme, 2 tamam. Peki 3, kendisi de bir çekici olan muntazam bir altkümesi var mı? Bir noktanın altkümesi nedir ki? Herhalde boş küme olur bu, ve bu çekici sayılabilecek bir şey değildir, 3 tamam.

Soru

Çekiciler illa nokta mı olmalı?

Cevap

Hayır. Bir limit çevrimi de çekici olabilir. Mesela içinde gayri-stabil bir nokta içeren stabil bir limit çevrimi düşünelim, herşey bu çevrime doğru çekiliyor. Değişmezlik var mı? Evet. Çevrimde başlarsam orada kalırım. Açık küme başlangıç şartlarını çeker mi? Evet. Orijin haricinde [çevrim orijin merkezli] her şey (çünkü orijinde gayri-stabil bir nokta var), ortasındaki ufak bir "delik" haricinde herşey bu çevrime çekilir, ki çekilenler bir açık küme oluşturur. Minimal midir? Eğer düşünürsek limit çevriminin üst kavisi mesela, bu değişmez değildir.

[bazi sorular atlandi]

İlginç 3 özellik bunlar. Çoğunlukla bir 4. özellik te ekliyor, herkes yapmıyor bunu, neyin ispat edilmek istendiğine göre değişiyor, ama genellikle yapılıyor. Bu özellik şöyle,

4) $A$ yakınında başlayan gidiş yolları tüm zaman $t > 0$ süresince $A$'ya yakın kalmalı.

Dikkat edersek bu 2. öğeden biraz farklı. "Açık küme başlangıç şartları çekilmeli" dediğimizde zaman sonsuza giderken ne olduğunu düşünüyoruz, nihayetinde $A$'ya yakın düştükleri sürece kısa vadede gidiş yollarının ne yaptığıyla ilgilenmiyoruz. 4 biraz daha "kontrol delisi" denebilecek bir şart, "$A$'dan hiçbir zaman uzaklaşmanı istemiyorum" diyor, yani fazla uzağa gitmeni istemiyorum diyor, bir anne, babanın çocuğuna söyleyebileceği şekilde belki.

Daha net olarak tanımlamak için, verili bir bölge $A$'nin $U$'şu ($U$, $A$'nin etrafında bir tür bant gibi görülebilir, örnek altta), bir $A$'nin $V$'sı denebilecek bir bölge vardır öyle ki $V$'de başlarsanız sonsuza kadar $U$'de kalırsınız.

Bir örnekte görmek daha faydalı olabilir. Bir faz portresi çizeyim (altta), bu tek boyutlu bir döngüyü temsil edecek, içinde birşey, bölge yok. Bir dışkı çevreleyen bir seymiş gibi duruyor ama o değil, ben sadece çemberin kendisinden bahsediyorum, daha önce çember üzerinde vektör alanlarından bahsetmiştik, onun gibi. Özel bir vektör alanından bahsediyorum ama, sistemde bir yarı-stabil nokta var.

Bu çemberdeki akış noktanın gayri-stabil tarafından çıkıp stabil tarafına doğru akıyor. Daha teknik olarak yazmak istesek ama, resme göre $\pi/2$'de bir çekici [gibi olan bir şey] var,

$$ \dot{\theta} = 1 - \sin\theta $$

yapabilirdik. $\theta^\ast = \pi/2$'da bir sabit nokta var, soru şu, gösterilen nokta bir çekici mi? Listeden kontrol edelim, orada başlarsak sonsuza kadar orada kalır mıyız? Evet. Bu bir sabit nokta. Açık küme başlangıç şartlarını çekiyor mu? Çektiği ne? Herşey. Çember üzerinde nerede başlarsanız başlayın, sonunda o noktaya gideceksiniz. Tüm çemberi çekiyor, ve çember açık. 1. ve 2. şartlarını tatmin eden muntazam bir altkümesi var mı? Hayır. Bu bir nokta, altkümesi yok. O zaman ilk 3 kriterime göre bu noktaya çekici demem gerekir.

Ama bazı yazarlar bu kararla hemfikir değil. "Yapma şimdi Steven" diyorlar, nokta neredeyse yarı gayrı-stabil, mesela saat 10 noktasında bir yerlerde başlasam geri dönmeden önce koca bir seyahat yapmam gerekecek, yani yarı-stabil noktaya yeterince yakın durmadım, noktanın etrafında bir ufak bölge çizmiş olsam o bölgeden kesin çıkacağım yani. Bu anne / çocuk örneğinde uzaklaşan çocuk oluyor, yani 4. şart ihlali. Bu arkadaşlar o sebeple bu noktaya "çekici değil" diyorlar.

Şimdi garip çekici derken neden bahsediyoruz onu anlatalım, yani torus, limit çevrimi olmayan bu şeyi nasıl tarif ederiz? Garip çekiciyi tariflerde de farklılık olabilir, bazısına göre başlangıç şartlarına hassas bağlantı yeterli. Ama bazıları geometrik özellikleri ön plana çıkartabiliyor, onlara göre "garip çekici yerel yapısı pürüzsüz değil ama fraktal olan bir çekicidir". Fraktalları ileride işleyince bu söz daha anlamlı olacak tabii. Bizim ifade dinamik bakış açısını ön plana çıkartıyor, öteki geometrik. Bizim tarif kaotik çekici olarak ta tarif edilir, ikincisi fraktal çekici. Bu konuda literatür biraz çoğulcu olabiliyor.

Lorenz Çekicisinin Dinamiği

Önceki derste resmi göstermiştik, Lorenz sisteminde iki büyük bölge vardı, gidiş yolları birinde bir süre dönüp dönüp sonra ötekine geçip benzer hareketleri yapıyordu, geri geliyor, vs. Bu ders kitabımın 9.4 bölümünden.

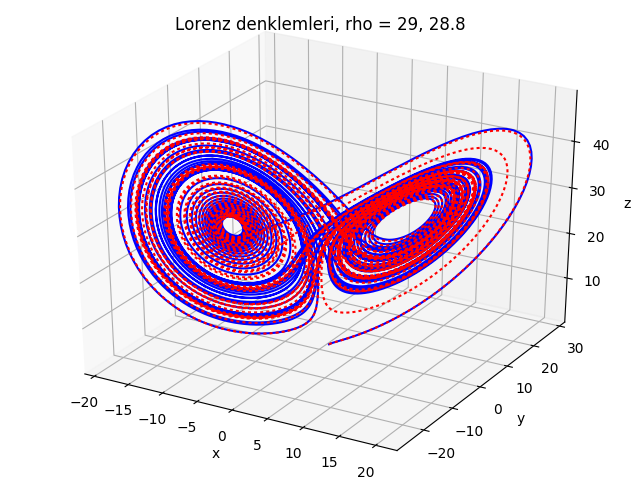
Lorenz'in burada yaptığı akıllıca iş şu idi, sistemini tek boyutlu eslemeye (1-d map) indirgedi. Makalesinin [1] ikinci figüründe bunu nasıl yaptığını gösteriyor, z-y grafiğini çiziyor, çekicisinin izdüşümünü bunun üzerinden yapıyor,

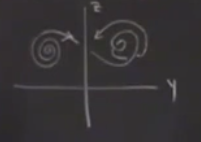
Sistemi için standart parametreleri kullanmış $r=28,\sigma=10,b=8/3$. Sonra şu yorumu yapıyor: "Bu gidiş yollarına bakınca, bir gidişin merkezden belli bir kritik uzaklığı aştıktan sonra içinde olduğu sarmaldan çıktığını görüyorum. Diğer sarmala giriş noktası çıkış öncesi olan mesafenin ne kadar büyük olduğuna bağlı gözüküyor". Ve devam ediyor "bir sarmaldan nerede çıktığınız ve ikincisinde nerede girdiğiniz, girdiğiniz sarmalda oradan da çıkmadan önce kaç tur atacağınızı da kontrol ediyor, ki bu da tabii diğer sarmala nereden gireceğinizi kontrol ediyor, böyle devam ediyor".

Lorenz'in yapmaya çalıştığı olanları daha ufaltılmış boyutlarda, özetsel bilgiler üzerinden anlamaya uğraşmak, mesela çıkış, giriş mesafeleri, tur sayısı, vs. Nihayet şu ifadeden bahsediyor, ifadesinde bir kelimenin altını çizmiş, o nokta önemli o yüksek sesle söylenecek, benim tarafımdan tabii, Lorenz'in kendisi Maine eyaletinden çok mütevazi, sessiz sakin bir insandı konuşurken onu zor bile duyardınız. Bir de çok monoton konuşurdu, dinlerken aklınıza saatinize bakmak filan gelirdi "acaba yemeğe gitsem mi şimdi?" gibi.. [öğrenciler gülüyor], yani hiç eğlenceli biri sayılmazdı. Fakat müthiş bir bilim adamıydı, ve çok iyi niyetli bir insandı. Neyse, vardığı nokta şu "[..] o zaman bir sarmalda ölçülen / takip edilen \underline{tek} bir özelliğin diğer onun diğer sarmalda tekabül eden halini tahmin etmek için kullanılması mümkün olmalıdır". Yani sürekli zamanda üç sayıyı [izdüşüm yapıldı, unutmayalım, üç boyut ikiye indi, sonra tek bir ölçüm bulundu] takip etmek yerine ayrıksal zamanda tek bir sayıya bakmak yeterli olacak, ve bu sayı bir sarmaldan diğerine takip edilebilecek.

Soru

Nasıl bir tür bir sayı bu?

Cevap

Birazdan söyleyeceğim. Şu anda tanımsız, Lorenz'in sezgisi işliyor şu anda, yaratcılık burada işin içine giriyor işte, tam tanımsız, belirsiz bir fikri var, tek bir sayının her şeyi takip etmek için kullanılabileceğini düşünüyor.

Şimdi çıkışı düşünelim, ne zaman bir sarmaldan çıkıyoruz? Bir maksimum $z$ değerine gelindiği zaman diyelim, sarmaldan çıkıp diğerine giriyoruz, sonra orada da bir yüksek noktaya erişiyoruz, ve çıkıyoruz. Lorenz bu maksimum değeri düşünmeye başladı.. bunu saptamak için $z$'yi bir zaman serisi olarak grafikledi,

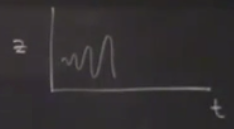
Sağa gittikçe büyüyen bir salınım bu, daha önce Lorenz sisteminin dinamiğinde gördük bunları. Lorenz sonra bir "n'inci maksimum ölçütü" diye bir şey tanımlıyor, bunlar yerel tepe noktaları,

İki boyutlu resimde bunlar sarmal üzerinde her halkanın saat 12 noktaları olurlardı. Soru şu, $z_n$'in $z_{n+1}$ üzerindeki etkisi nedir? Lorenz böyle bir etki olduğunu düşünüyor, grafiği onun için çizdi zaten, ve $z_n,z_{n+1}$ ilişkisine daha yakından bakmak istiyor, şimdi bilgisayarda buna bakalım [2].

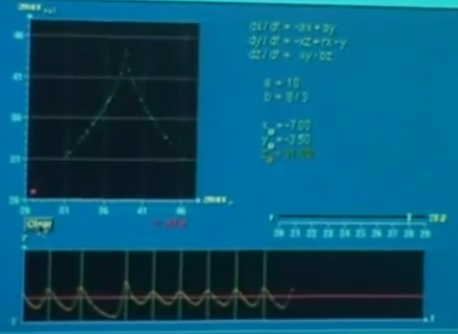
İki grafik var, alttaki $z,t$ grafiği. Onun üstündeki $z_n$ ve $z_{n+1}$ grafiği, yani bir tepe noktası ile ondan hemen sonraki tepe noktası eşlenerek grafiklenmiş, aradaki ilişkiyi görmek için. Bu noktalar orada burada dağınık bir şekilde olabilirdi, ama değiller, düzgün bir çatı şekli oluşturmuşlar. Lorenz bunu görünce diyor ki "bu bir fonksiyonun grafiğine benziyor", yani o şekli üreten bir fonksiyonun olduğunu seziyor, ve dinamik sistem bu fonksiyondan "örneklem alıyor" bir bakıma. Şimdi bu düşünce zincirini daha da ilerletelim ve sistem açısından ne demek olduğunu anlamaya uğraşalım.

Bilgisayarda oluşan grafiği tekrar çiziyorum (kesikli olan çizgi 45 derece açıyla karşılaştırma amaçlı çizdim, bir diğer sebebi daha var ona geleceğiz),

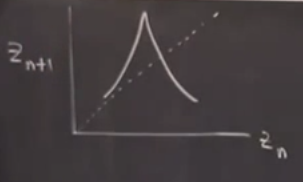
Bir fonksiyon var ise, bu $z_{n+1}=f(z_n)$ olarak belirtilebilir. Bilgisayar çıktısına dikkat edilirse grafiğin genişliği neredeyse yok. Aslında sonradan ortaya çıktı ki böyle bir fonksiyon analitik olarak yok, fakat eğer olsaydı bunun anlamı ne olurdu? Bu düşünce çizgisini inceliyoruz.

Lorenz önce grafiğin eğimine baktı, eğimin mutlak değeri her zaman 1'den büyük, yani $|f'(z)| > 1$, $\forall x$.

Bu fonksiyonu "işletmek" istersek ne yaparız? Yani $z_{n}$ vereceğiz, $z_{n+1}$ çıkacak, onu verip $z_{n+2}$ elde edeceğiz, hani hesap makinalarında bazılarımızın yapmış olabileceği gibi sinüs ya da karekök tuşuna ardı ardına basmak, ve sonuçlara bakmak [böylece bir önceki çıktı sonraki girdi olur bir anlamda].

Bu işletmeyi grafiğin üzerinde yapabiliriz aslında, ve onu yaparken şu sorunun cevabını arayabiliriz, girdiye verilince sonuç kendisi olan bir rakam var mıdır? Tahmin edebileceğimiz üzere bu bir stabil nokta olurdu, çünkü oraya varınca hep orada kalınır. Daha önce çizdiğimiz 45 derece kesikli çizgi burada bize yardımcı olur, o kesikli çizgideki noktalar istediğimiz özelliklere sahip [tanım itibariyle orada her nokta kendisine eşit], o zaman bu kesikli çizginin $f$'yi kestiği yer $f$'te aradığımız sabit noktadır.

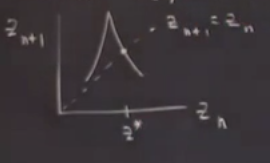
Üstteki grafikte bu sabit noktayı görüyoruz, $z^\ast$ ismini verdik, $f(z^\ast) = z^\ast$. Sabit noktalar diferansiyel denklemlerdeki sabit noktalar gibi burada sabit nokta özyineli eşleme (iterated map) için.

Ama biraz önce gördüğümüz animasyonda o $z^\ast$ noktasına hiç gelmedik, çünkü eğer gelseydik orada takılı kalırdık. Lorenz bu noktanın stabilitesine baktı ve gayrı-stabil olduğunu gördü [herhalde bu sebeple gözlemlenmesi zor çünkü oraya doğru çekiliş yok].

Fakat unutmayalım üstteki grafik üç boyutlu uzayda o kanatlı sekizimsi grafiği bir nevi özetleyen, onu baz alan bir grafik. Acaba üstteki grafikteki sabit noktanın o üç boyutlu grafikteki karşılığı ne olurdu? Gidiş yolu bağlamında yani, özyineli eşlemede $n$'inci maksimumun $n+1$'inci maksimum ile aynı olması gidiş yolu bağlamında ne demektir? Hatırlarsak izdüşüm grafiğinde $z$ içeriden dışarı doğru büyüyor.. burada öyle $z$ hep aynı kalacak.. Dik duran tam bir sekiz figürü bunu yapabilir,

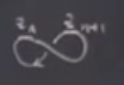
$z_n$ ve $z_{n+1}$ aynı yükseklikte.. Bu döngü, ki Lorenz çekicisi üzerinde olası bir döngü, özyineli eşlemedeki sabit noktaya tekabül ediyor. Bu Lorenz sisteminde olası bir periyodik yörünge bu arada, acaba stabil mi? Bir limit çevrimi var, bir stabil limit çevrimi mi? Cevap hayır, ve argüman çok basit. Argüman için grafik metot kullanabilirdik, ya da lineerleştirme kullanabilirdik. Önce lineerleştirme ile yapalım,

$$ z_n = z^\ast + \eta_n$$

$\eta_n$ ufak bir sarsım (perturbation), o zaman $|\eta_n| << 1$. $z^\ast$ etrafında lineerleştirme yapmak istiyoruz, üstteki tanımdan hareketle,

$$ z_{n+1} = z^\ast + \eta_{n+1} $$

Diğer yandan $f(z_n)$ açılımını yapalım,

$$ f(z_n) = f(z^\ast + \eta_{n+1}) = f(z^\ast) + \eta_n f'(z^\ast) + O(\eta_n^2) $$

$O()$ terimlerini yok sayabiliriz çünkü lineerleştirme yapıyoruz. Lorenz eşlemesine göre $z_{n+1} = f(z_n)$, o zaman üstteki ile iki üstteki eşitliğin sol tarafları aynı, yani bu eşitliklerin sağ tarafları aynı.

$$ z^\ast + \eta_{n+1} = f(z^\ast + \eta_{n+1}) = f(z^\ast) + \eta_n f'(z^\ast) + O(\eta_n^2) $$

Ve farkedelim ki tanım itibariyle $f(z^\ast) = z^\ast$, ve $O$ terimlerini atıp eşitliği yaklaşık temsil haline getirirsek,

$$ \cancel{z^\ast} + \eta_{n+1} \approx \cancel{f(z^\ast)} + \eta_n f'(z^\ast) $$

Elimizde $\eta_{n+1}$ için bir ifade kaldı, bu ifade bize sapma $\eta$'nin her döngüde nasıl büyüdüğünü ya da çürüdüğünü gösterecek.

$$ \eta_{n+1} \approx f'(z^\ast) \eta_n $$

Bunu analiz etmek kolay, $\eta$ büyüyor mu çürüyor mu? Hatırlarsak daha önce belirtmiştik ki $|f'(z)| > 1$, o zaman $|f'(z^\ast)| > 1$'da doğrudur. Bu durumda,

$$ |\eta_{n+1}| > |\eta_n| $$

doğru demektir, bu sapmalar büyüyor demektir, demek ki $z^\ast$ bir gayri-stabil noktadır.

Lineerleştirme yerine grafik kullanabilirdik, bu grafiklere birazdan göreceğimiz girift şekli sebebiyle örümcek ağı diyagramı (cobweb diagram) deniyor.

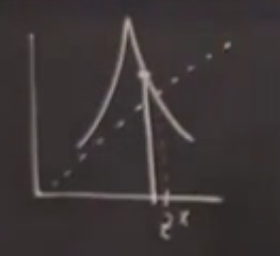
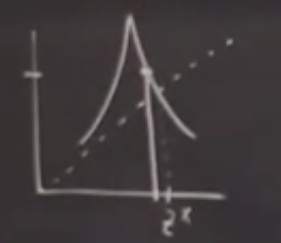
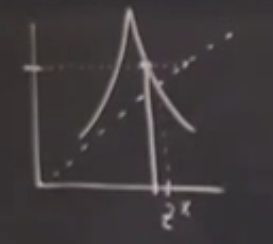
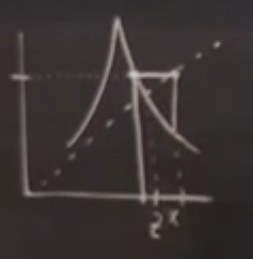
Nasıl çizildiğini tarif edelim. Başlangıçta diyelim $z^\ast$'nin az solunda bir yerlerdeyiz. Bu anda $x-y$ bakış açısındayız, fonksiyona giren, çıkan ne olduğu açıkça belli, yatay eksenden yukarıya çıkıyoruz (1. resim) ve fonksiyona nerede deyiyorsak orası fonksiyonun oradaki değeri, dikey eksende bu değeri görüyoruz, fonksiyondan sola gidip orayı işaretleyebiliriz (2. resim). Peki şimdi çıktıyı girdi yapmak için ne yapmak lazım? Burada 45 derece yatay olan çizgi numarası kullanabiliriz, dikey eksendeki bir değeri yatay eksendeki yerini bulmak için (mesela dikeyde 3'ten yataydaki 3'e nasıl gideriz?) bu en rahat yol, mesela dikeyde 3 değerinde isek oradan sağa doğru gidip 45 derece çizgiye çarpıncaya kadar devam ederiz, oradan aşağı inerek yatay eksendeki aynı değere ulaşırız (4. resim). Şimdi bu çıktıyı bir sonraki girdi yapmak için aynı işlemi tekrarlamak için aynı şekilde yukarı çıkıp tekrar fonksiyona çarpamaya uğraşırdık, 4. resim bir kestirme kullanmış, aşağı inerken fonksiyona çarptığı yerde durmuş, bir daha in-çık yapmamış. Farketmez.

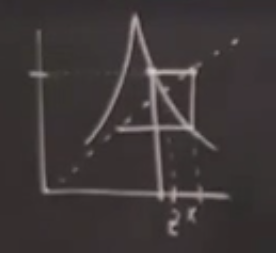
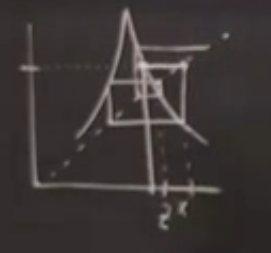
Devam ediyoruz, tekrar sola, oradan yukarıya gidip fonksiyon değerini alıyoruz, ve bu şekilde devam ediliyor. Diyagrama niye örümcek ağı dendiği de görülüyordur, ağımsı bir şekil oluştu. İşte grafiksel özyineleme böyle yapılıyor.

Peki belli bir $z$ etrafında odaklanılıyor mu acaba? Üstteki örnekte olmuyor ama biraz hoca hilesi yapayım (!) grafiği değiştirip tekrar eder hale getireyim,

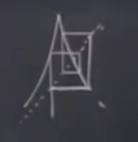
Evet. Şimdi burada bir periyodik yörünge var (tek $z$ etrafına odaklanma olmasa da), sürekli o döngünün içinde dönüp durulacak. Soru şu, sabit nokta stabil olmasa da stabil olan bir periyodik yörünge var mıdır acaba? Kontrol edelim. Periyodik yörüngeyi nasıl tarif ederiz? Üstteki periyodik yörünge bir $z_1,z_2,z_3..,$ sayı dizisini üretiyor diyebiliriz ve bu dizi bir süre sonra kendini tekrarlamaya başlıyor, yani $z_{n+p} = z_n, \quad \forall n$ oluyor ki $p$ periyot. Bizim örnek resimde periyot $p=4$ [hoca çizgileri takip ederek başa ne zaman döndüğüne baktı, ve $z_5=z_1$ buldu].

Periyodik yörünge stabil midir? Bu arada büyük resmi gözden kaçırmayalım, tüm bunları niye yapıyoruz? Lorenz şu anda kendine şunu soruyor, gördüğü çekici aslında stabil bir limit çevriminden ibaret mi? Bunu anlamaya uğraşıyor. Daha önce biz ilk baştaki parametrelerle Lorenz sisteminde stabil limit çevrimi yoktur demiştik, bunu nereden biliyoruz? Eğer bu doğru olsaydı örümcek ağı diyagramı o periyotluk şartına uygun noktalar üretirdi, bunun olmadığını göstereceğiz, bu da aslında $f$'nin eğimi ile alakalı, sorun bu olacak.

Devam edelim, $z_{n+p} = z_n$ formülüne bakalım, ve eger $p$ kere donersek,

$$ z_2 = f(z_1)$$

$$ z_3 = f(z_2) = f(f(z_1)) = f^2(z_1) $$

Kare işareti bu arada bildiğimiz kare almak değil, içiçe iki kere $f$ demek. Böyle devam edersek,

$$ z_4 = f^3(z_1) $$

Burada ortaya çıkan kalıba göre

$$ z_{n+p} = f^p(z_n) $$

olurdu. Dikkat edersek periyot sayısı $z_4 = f^3(z_1)$ formülünde $4=3+1$, $f$'nin kaç kere içiçe çağrısının olduğu artı ona başta verilen $z$ indisi.

Tanım

$z$, $p$ periyoduna sahip bir noktadır eğer $f^p(z) = z$.

Bu ifade bir sabit noktanın genellenmiş hali, sabit nokta üstteki $p=1$ hali, yani $f^1(z) = f(z) = z$ tanımına uyan şey. Periyot iki noktası $f^2(z)=z$, iki kere dönüldükten sonra tekrar oluyor. Ayrıca $p$ tekrar özelliğine sahip en küçük tam sayı alınır, $p=2$ ile tekrar eden bir şey doğal olarak $p=4$ için de tekrar edecektir, ama burada $p=2$ kullanılır.

Bu tanımdan sonra esas söylemek istedidiğimize gelelim, tüm periyot $p$ noktaları gayrı-stabildir. Sabit noktanın gayrı-stabil olması gibi, $p$ periyot noktası da böyledir. İspat çok basit, $p=2$ için yapalım herhangi bir periyot için oradan anlaşılacak.

Periyot 2 için, diyelim ki $f(f(z)) = z$. Şimdi lineerleştirme yaparak stabiliteyi kontrol edebiliriz. Daha önce vardığımız bir sonucu hatırlarsak, sapmanın $z$ noktasında $f'$ tarafından belirlendiğini gösterdik. Şimdi $f$ in türevi yerine $f^2$'nin türevi lazım. Eğer mutlak değer 1'den büyükse gayrı-stabillik durumu var.

$$ (f^2)' = \frac{d}{dz} ( f(f(z)) ) = f'(f(z)) f'(z) $$

Şimdi $(f^2)'$'in büyüklüğü (magnitude) nedir, 1'den büyük müdür?

$$ |(f^2)'| = |\frac{d}{dz} ( f(f(z)) )| = |f'(f(z)) f'(z)| = | f'(f(z))|\cdot|f'(z)| $$

Şimdi daha önce yaptığımız beyan gelip bizi yine buldu, $f'$ her yerde mutlak değer olarak 1'den büyüktür demiştik.

$$ = \underbrace{| f'(f(z))|}_{>1} \cdot \underbrace{|f'(z)|}_{>1} > 1 $$

Demek ki bir stabil periyot yoktur. Aynı argümanı kullanırsak, ama 2 yerine $p$ faktörler kullanarak, hiçbir periyotta stabil periyodik nokta yoktur sonucuna varabilirsiniz. İşte Lorenz'in niye sisteminde stabil limit çevrimi olmadığı hakkında öne sürdüğü argüman buydu. Tabii bu tam geçerli bir argüman değil çünkü $f$ gerçekten bir fonksiyon değil, ama olsaydı, ispat tam yerine otururdu. Bunu ispata çevirme işinde Lorenz'den sonra bazı bilimciler aktif çalıştı, o ispat denemeleri üstteki değil başka fikirleri kullandılar ama yine de şunu herhalde görmüşüzdür, hiçbir stabil limit çevrimi olmadığını düşünmek için sağlam sebepler var.

Kaynaklar

[1] Lorenz, Deterministic Nonperiodic Flow, http://eaps4.mit.edu/research/Lorenz/Deterministic_63.pdf

[2] Strogatz, Ders #18 Video, https://www.youtube.com/watch?v=ERzcine5Mqc&t=2454