Ders 16

Bu derste su çarkı denklemlerini hızlıca analiz edeceğiz, ama hemen ardından onları bırakıp yakından alakalı kaosta herkesin incelediği ama daha iyi bilinen Lorenz denklem formuna geçeceğiz.

Su çarkı sistemini en son bıraktığımız nokta neydi? Bir mucizeyi gözlemledik! Sonsuz tane denklem içinden üç tane denklem kaldı, bu üç ODE geriye kalanlardan tamamen bağımsızdı. Tekrar yazarsak,

$$ \dot{a_1} = \omega b_1 - K a_1 $$

$$ \dot{b_1} = -\omega a_1 + q_1 - Kb_1 $$

$$ \dot{\omega} = \frac{-v\omega}{I} + \frac{\pi gr a_1}{I} $$

$\omega$ çarkın açısal hızıydı, sola ya da sağa ne kadar hızla döndüğünü temsil ediyordu. $a_1,b_1$ çark etrafındaki su dağılımının ilk harmoniğinin genlikleri idi [harmonik Fourier açılımındaki ilk $\sin,\cos$ terimlerine deniyor]. Galiba bizim formülasyona göre $a_1$ $\sin\theta$ için idi, evet evet, $b_1$ ise $\cos\theta$ içindi. Geri kalanlar sistemi tanımlayan sabit / parametreler, $v$ dönme direnci (fren), $K$ suyun akma oranı, $r$ yarıçap, $g$ efektif yerçekim etkisi, $q_1$ giren suyun ilk harmoniği.

Bu şimdiye kadar gördüğümüz ilk üç boyutlu sistemimiz. Onu analiz etmek için ne yaparız? İlk refleksimiz herhalde sabit noktalarını bulmaya uğraşmak. Sonra bu noktalar etrafında lineerizasyon düşünebilirim, aslında onu bu sistem için yapmayalım, Lorenz sistemi üzerinde yapalım daha iyi. Ama sabit noktalara bakalım. Bu noktaları bulmak için biraz cebirsel işlem gerekli, ve bu sabit noktaların bu sistem için ne anlama geldiği hakkında biraz kafa yormamız gerekli.

$$ \dot{a_1} = 0 \implies a_1 = \frac{\omega b_1}{K}
\qquad (1) $$

$$ \dot{b_1} = 0 \implies \omega a_1 = q_1 - K b_1 \qquad (2) $$

$$ \dot{\omega} = 0 \implies a_1 = \frac{v \omega}{\pi gr} \qquad (3) $$

$a_1,b_1,\omega$'yi bulmak istiyoruz, o zaman üstteki denklemlerde biraz temizlik, cebirsel manipülasyon yapabiliriz. (1) ve (2)'yi birleştirince $a_1$'den kurtulabiliriz. (2)'deki $a_1$ için (1)'dekini sokalım ve $b_1$'i bulalım, sonuç

$$ b_1 = \frac{K q_1}{\omega^2 + K^2}
\qquad (4) $$

$a_1,b_1$ için yıldız kullanabilirdim, $a_1^\ast,b_1^\ast$ gibi ama sabit nokta olduklarını biliyoruz, bunu atlayacağım. (1) ve (3) ile

$$ \frac{\omega b_1}{K} = \frac{v \omega}{\pi gr}$$

Üsttekinin en basit çözümü $w=0$'da çünkü her iki tarafta da bölünende $\omega$ var. Ama çözüm sıfır değilse diğer çözüm için her iki tarafı $\omega$ ile böleriz, ve

$$ b_1 = \frac{K v}{\pi gr} \qquad (5) $$

elde ederiz. Bu iki durumu biraz düşünelim, $\omega=0$ durumu ne demektir? Eğer $\omega=0$ ise (1)'e göre $a_1 = 0$, (2)'ye göre $b_1 = q_1 / K$. $\omega=0$ demek, çark dönmüyor demektir. $a_1=0$ ise içeri akan suyun sinüssel harmoniği yoktur, tepede simetrik bir dağılım vardır, ve $b_1$'e göre $q_1$ akış hızı $K$ ile dengelenmiştir, yani su akıyor ve olduğu gibi dışarı çıkıyor. Başka bir hareket yok. Bu bir sabit nokta, çünkü suyun dağılımında hiçbir değişim yok, su o yeşil kutucuklar içinde hep aynı histogram şeklinde duruyor. Diğer parametreler ne olursa olsun bu çözüm her zaman olası bir çözümdür. Stabil olduğunu söylemiyoruz, ama mevcut olduğunu söylüyoruz.

$\omega \ne 0$, o zaman

$$ b_1 = \frac{Kv}{\pi gr} = \frac{K q_1}{\omega^2 + K^2} \implies \omega^2 = \frac{\pi gr q_1}{v} - K^2 $$

Bu formül kalıcı durumda (steady state) diğer parametreler bazında dönüş hızının ne olacağını tahmin ediyor. Ayrıca dikkat edersek çözüm $\omega$'nin karesi bazlı, yani $\omega^2$, burada söylenmek istenen eğer $\omega$ bir çözüm ise $-\omega$ da bir çözümdür, dönüş herhangi bir yönde olabilir.

Tabii bu çözüm sadece ve sadece eşitliğin sağ tarafı pozitif ise mümkündür, bunu matematiksel olarak şu şekilde ifade edebiliriz,

$$\frac{\pi gr q_1}{K^2 v} > 1$$

Bu ifadeyi düşünüp tartmak daha kolay, çünkü bir sürü işlem sonucunu tek bir sayıyla karşılaştırıyoruz, bu hesap bir boyutsuz grup [boyut analizini hatırlarsak], birimi yok. Bu boyutsuz grup bilimde ünlü, yani su çarkı deneyi dışında da ünlü, sıvı mekaniği dalında taşınımı (convection) inceleyenler bu sayıya Reyleigh sayısı diyor.

Taşınımı hatırlamayanlar için üzerinden geçelim; bildiğimiz gibi güneş yeri ısıtır, o yer üzerindeki hava sıcaklaşınca yukarı çıkar, fakat aslında bu hareketin olması teorik olarak şart değildir. Fiziksel olarak düşünürsek hava hiç hareket etmeden havanın sıcaklığı yukarıdan aşağı doğru hareket ediyor olabilirdi, değil mi? Sıcaklık transferine iletim (conduction) adı veriliyor. Fakat yer ile hava arasındaki sıcaklık farkı yeterince büyükse, yani yeterince büyük bir ısı gradyanı var ise [ısı farkını hem yön hem büyüklük açısından bir vektör gibi görebiliriz] o zaman sistemin iletim çözümü gayrı-stabildir, bu durumda ısı yerine hava hareket etmeye başlar, sıcak hava yükselir, yukarıda soğur, soğuyunca yoğunlaşır, yoğunlaşınca aşağı inmeye başlar, ve ortaya "taşınım hücresi" adı verilen denen bir devridaim süreci ortaya çıkar.

Bu anlatılanların üstteki formül ile ne alakası var? Dönen su çarkı sanki bir taşınım hücresi gibidir, kalıcı durum hali ise bir nevi iletimdir. Çarka giren su ile ısı gradyanı arasında parallellikler var. Malkus çarkını tasarlarken tüm bunları biliyordu, taşınım konusunda uzmandı, çark ufak bir taşınım hücresinin modeli olacaktı.

Her neyse, üstteki formüle dönersek, bu formül ne söylüyor? Bölünen ile bölende neler olduğuna bakalım: bölünende yerçekimi, içeri akan suyun yarattığı ivme gibi faktörler var ki bunlar çarka dönme hızı veren faktörler. Diğer yandan yitirgenlikle (dissipative) alakalı terimler bölende, $K$ suyun dışarı akışı, $v$ frenleme, bu faktörler dönmeye durduran faktörler. O zaman üstteki formül döndüren ve onu durduran kuvvetler arasında bir savaşı temsil ediyor, eğer bölünendeki değer bölendekinden daha yüksek ise tüm hesap 1'den yüksek olacaktır, tam tersi için 1'den küçük olacaktır. 1'den büyük ise dönmeyi ima eden çözümler mevcut demektir.

Bu noktada güzel su çarkına bye-bye, ondan da güzel Lorenz sistemine hoşgeldin diyoruz. Yani daha güzel değil tabii, neredeyse aynı şeyler [lafın gelişi].

Lorenz Denklemleri

Bu arada bilim tarihinde birkaç tane Lorenz var, bizim bahsettiğimiz MİT'de atmosfer bilimci olan Ed Lorenz, birkaç sene önce vefat etti, benzer isimli bir diğer bilimci Lorentz [t ile], bu bilimci fizikte iyi bilinir, Poincare ile aynı yıllarda yaşadı, fizikte Lorentz kuvveti denen bir şey var, bu Hollandalı Lorentz bizimkinden farklı. Bir de Conrad Lorenz var, o da davranışsal biyolog idi, bu Lorenz ördeklere arkasından yürümeyi öğretmiş. Ördekler doğduğunda anneleri yerine Lorenz'i görmüşler, onu anneleri zannedip arkasından yürümeye başlamışlar.

Neyse bizim Lorenz, Ed Lorenz ile ben tanışma şansına eriştim. Çok iyi, mütevazı bir insandı, ve inanılmaz bir keşfe imza attı, merak edenler James Gleick'ın kitabına bakabilir. MIT'deyken onu derslerime misafir eğitmen olarak bazen çağırırdım, çünkü bu alanın devlerinden biri kendisi, ilginç bir hikaye: ne zaman derse çağırsam, hoca bana soruyor: "hangi konu hakkında konuşayım?". Ben de derdim ki "Lorenz denklemleri tabii ki hocam [gülüyor]". O da derdi ki "Ah şu ufak model mi?". Yani hoca artık başka konulara geçmiş, ve o anda üzerinde çalıştığı şeylerden bahsetmek istiyor, ben de tamam diyordum, ve bu dersler hep çok ilginç oluyordu. Bu sırada Ed 80 yaşlarında civarında ama hala sıkı bir çalışma içinde. Lorenz'e bir türlü Lorenz denklemlerini anlattıramadık yani. Bu herhalde Einstein'e izafiyet denklemlerini anlattırmak gibi bir şeydi belki de.. O eski denklemler mi? Yapılmış bitmiş işler bunlar!

Lorenz'in denklemleri hakkındaki onun makalesini [2] okumanızı tavsiye ederim, makale taşınım ile alakalı, Lorenz modelini basit bir taşınım modelinden başlayarak türetti. Yaptığı araştırmanın önemli olmasının sebeplerinden biri içinde bir kaotik çekici (attractor) içeren ilk sistem örneği olması. Lorenz kaosu keşfetmedi, kaos teknik olarak 1800'lerin sonunda Poincare tarafından bulunmuştu, Poincare üç cisim problemini inceliyordu, fakat onun baktığı modelde kaotik çekici yoktu, bir tür geçici kaos durumu vardı, yani sistem bir süre çetrefil bir halde davranıyor, sonra o durumdan çıkıyor. Lorenz'in sisteminde kendini besleyen bir tür kaos var - bir başlayınca, öyle devam ediyor.

Lorenz denklemleri,

$$ \dot{x} = \sigma (y - x) \qquad (6) $$

$$ \dot{y} = rx - y - xz $$

$$ \dot{z} = xy - bz $$

Görüldüğü gibi aynen su çarkı denklemleri gibi üç boyutlu bir sistem bu. $\sigma,r,b > 0$ olacak şekilde parametreleri var, sistem değişkenleri $x,y,z$ pozitif ya da negatif olabilir. Değişkenlerin sıvı akış mekaniği bağlamında anlamı nedir diye düşünülebilir, bunun hakkında fazla düşünce sarf etmeye gerek yok, onları soyut büyüklükler olarak görebiliriz, bizim için daha fazlasına ihtiyaç yok. Ama su çarkı ile alakayı düşünmek istersek, hatırlarsak, su çarkında iki tane karesel gayrı-lineerlik vardı, $\omega a_1$, $\omega b_1$. O değişkenler üstteki $xz$ ve $xy$ ile bir şekilde bağlantılı, ki $xz,xy$ üstteki denklemdeki yegane karesel gayrı-lineerlikler. Ayrıca $r$ Rayleigh sayısı, bu kavramı daha önce görmüştük. Lorenz denklemleri sadece akışkan sistemlerle sınırlı değildir, taşınım, su çarkı gibi, bilimin diğer kısımlarında da ortaya çıkar, mesela lazerler.

Üstteki sistemi incelerken felsefemiz şu olacak; önümüzde korkutucu üç boyutlu bir sistem var, tabii ki elimizde sabit noktalar, stabilite kontrolü gibi araçlar var ve bunları kullanacağız, ondan sonra çözüm için elimizde ne varsa bu problemin üzerine atacağız, ki bunu yaparken aslında Lorenz'in yaptıklarının tekrar etmiş olacağız. O böyle yapmıştı çünkü yapmak zorundaydı, şimdiye kadar kimse üç boyutlu gayrı-lineer dinamik sistemleri incelememişti, onlar hakkında pek çok şey bilinmiyordu. Elimizde neler var? Limit çevrimlerini bulmak, çatallaşmalara bakmak. Bunları yapacağız ve göreceğiz ki belli parametreler çevresinde bildiğimiz hiçbir şey geçerli değil. Stabil nokta yok, stabil limit çevrimi yok, periyotsalımsılık yok, ama bir şeyler var. Ne var? Lorenz'in kullandığı düşünce şekli buydu, ünlü detektif Sherlock Holmes gibi mümkün olmayan her şeyi eledi ve geriye kalan, her ne kadar olası olmasa da, gerçeğin kendisi olmalıydı. Bu durumda geriye kalan şimdiye kadar hiç görülmemiş bir kavram, kaos olacaktı.

Önce basit özelliklerden başlayalım.

1) Değişken değişimi $(x,y) \to (-x,-y)$ bağlamında sistemin simetrik. Yani bahsedilen değişken değişimi yapılınca üstteki sistem aynı kalacak. Mesela sistemdeki 1. formülde $x,y$ işaretlerini değiştirdik, parantez içinde $y-x$ işaret değiştirir, ama $\dot{x}$ te işaret değiştireceği için negatif değişimler birbirlerini iptal eder. 2., 3. formüller benzer şekilde.

Simetriklik ne anlama gelir? Eğer elimizde $x(y),y(t),z(t)$ çözümleri var ise, o zaman çözümün bir "simetrik kardeşi de" var demektir, $-x(y),-y(t),-z(t)$ de bir çözümdür (başlangıç şartları değişik olabilir). Çözümlerin, eğer özgün iseler, çifter çifter geldiğini de düşünebiliriz. Bazen çift çözümlerin ikisi de aynı şey olur, bu durumda çözümü kendisinin bir simetriklik içerdiği söylenir, bu tür şeyler göreceğiz, simetrik çözümler ya da simetrik bir çift çözüm.

2) Sistem "yitirgen", faz uzayındaki hacimler akış sonrası ufalıyor

Ne demek istediğimi açmaya uğraşayım: bu örnekte üç boyutlu uzayda yaşayan bir başlangıç durumundan zaman geçtikçe bir gidiş yolu başka bir noktaya gider, arkada geçilen noktaları bir eğri gibi düşünelim. Şimdi bir tane yerine birden fazla başlangıç noktası hayal edelim, bu noktaların hepsi bir patates şeklinden (içi, dışı) geliyor olsunlar.

Gelinen noktaların hepsini beraber düşünürsek ortaya bir deforme olmuş patates çıkacağını düşünebiliriz. Tabii başlangıcın illa patates olması gerekmiyor, küre, herhangi bir şekil olabilir. Ben patates dedim çünkü üç boyutlu genel bir kütlenin hayal edilmesini istedim. Neyse, iddia şu ki Lorenz sistemi için akış sonrası gidilen deforme patatesin hacmi başlangıç patatesinden küçüktür. Zaman geçtikçe hacim daha da küçülür. "Yitirgen" ile bunu kastediyoruz. Yitirgenlik birörnek (uniform) olmayabilir, bir yönde az, diğer yönde daha fazla olabilir, fakat hacmin tamamında bir azalma vardır.

Bu azalmayı görmek için kendimize şu soruyu soralım: hacim nasıl değişir? Herhangi bir başlangıç hacmi $V(t)$'yi olsun, takip etmemiz gereken yegane noktalar hacmi yüzeyinde olanlar, ve bu noktalardan başlayan gidiş yolları sistemin vektör alanına göre akıyor olacaklar, o zaman bir süre sonra $V(t + \Delta t)$ hacmi nedir? Bunu görmek için hacim için bir diferansiyel denklem türeteceğiz. Hacim derken hacmi gösteren o tek sayıdan bahsediyorum, tüm bölgenin şeklinden bahsetmiyorum.

Önce sezgisel argüman, notasyon

$$ \underline{x} = (x,y,z)$$

$$ \underline{u} = \dot{\underline{x}} $$

olsun, yani $\underline{u}$ bu üç boyutlu faz uzayındaki hız. Bunlar şimdiye kadar gördüğümüz şeyler, bir diferansiyel denklem olduğu zaman onun faz uzayındaki vektör alanını düşünüyoruz, ki bu alan bize her noktada bir vektör veriyor. Dikkat edelim, sıvı mekaniğiyle başladık şimdi "hız" dedik, ama bu hız sıvının akış hızı değil, faz uzayındaki soyut hızdan bahsediyoruz.

Peki bu hızın hacmin yüzeyine dik olan bileşeni nedir? Eğer yüzeye dik bir $\underline{n}$ vektörü düşünürsek, $\underline{u}$'nun o yöndeki bileşeni $\underline{u} \cdot \underline{n}$ olur, biraz önceki eşitlik üzerinden ${\partial V}$ için (kısmi türev sembolü kullanıldı ama buradaki anlamı "$V$ sınırı, onun dış çeperi")

$$ \underline{u} \cdot \underline{n} = \dot{\underline{x}} \cdot \underline{n} $$

${\partial V}$ yerine $S$ de kullanılabilir.

Sorumuz $\Delta t$ zamanı sonrası hacim nedir? Yani $V(t + \Delta t)$.

Hacim değişimini zihinde canlandırmak için genel bağlamda genişlemeyi modellemeye uğraşalım, $V$'nin dışında daha büyük bir patates hayal edelim (küçülme de aynı mantık üzerinden hallediliyor) $V$ ona evrilmiş olsun,

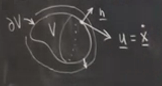
Resmin alt kısmındaki ok yüzeydeki bir noktanın nasıl genişlediğini gösteriyor, ve diğer bir noktaya göre $\underline{n}$ gösterilmiş, ve hız vektör alanının o noktadaki hali $\underline{u}$. Çizim bizi aldatmasın, $\underline{u}$'yu teğet yapmaya uğraşmadım.

Modelleme açısından şöyle düşünebiliriz, hacmin genişlemesi hızın yüzeydeki normal bileşeni üzerindendir. O sebeple $\underline{u} \cdot \underline{n}$'e odaklandım, çünkü hacim genişleme açısından bizi ilgilendiren en önemli büyüklük bu. İddia şöyle, yeni $V(t + \Delta t)$, eski $V(t)$ artı hızın normal yönde aştığı bir ufak bölgenin tüm mümkün bölgeler üzerinden entegre edilmiş halidir.

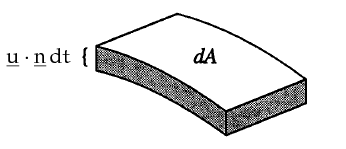
Üstte gösterilen ufak parçanın hacim değişimi yaklaşık olarak

$$ \Delta V \approx (\underline{u} \cdot \underline{n} \Delta t) \mathrm{d} A $$

O zaman, tüm bölgeler için

$$ V(t + \Delta t) \approx V(t) + \Delta t \iint\limits_{\partial V} \underline{u} \cdot \underline{n} \mathrm{d} A $$

Üstteki argüman tabii ki kulağa küpe / tahminsel / kestirme (heuristic) bir argüman. Entegrale dikkat, bu bir yüzey entegrali. Eğer akı (flux) bazlı düşünmek istersek üstteki hesap vektör alanı $\underline{u}$'nun dış akısı olarak görülebilir.

Soru

Entegral niye yaklaşıksal, kesin değil?

Cevap

$\Delta t$'yi limitte sıfıra götürdüğümüzde kesin olacak.

Devam edelim, $V(t)$'yi sola geçirelim ve tüm formülü $\Delta t$'ye bölelim.

$$ \lim_{\Delta t \to 0} \frac{ V(t + \Delta t) - V(t)}{\Delta t} = \dot{V(t)} = \iint\limits_{\partial V} \underline{u} \cdot \underline{n} \mathrm{d} A $$

Nihai amacım bu formüldü, formül bana hacmin nasıl değiştiğini gösteriyor, ki $\dot{V(t)}$ hacim değişimidir. Bu arada Çok Değişkenli Calculus dersini almış olanlar için üstteki çift entegral tanıdık gelebilir, formülün yapısı uzaklaşım (divergence) teorisini uygulamaya hazır, o çift entegral $\underline{u}$'nun uzaklaşımının üçlü entegraline eşittir, yani

$$ \dot{V} = \iint\limits_{\partial V} \underline{u} \cdot \underline{n} \mathrm{d} A = \iiint \nabla \cdot \underline{u} \mathrm{d} V $$

Hacmin üç boyutlu faz uzayında herhangi bir vektör alanında nasıl değiştiğini tarif eden formüller bunlar. Gerçi tahmin ederim ki boyut ne olursa olsun formüller geçerlidir ama biz şimdilik üç ile kendimizi sınırlayalım.

Şimdi bu genel formülleri özelde Lorenz sistemine uygulayalım. Üçlü entegralde bir $\underline{u}$'nun uzaklaşımından bahsediliyor. Lorenz sisteminde $\underline{u}$'nun uzaklaşımı nedir? $\dot{V}$ formülünü tekrar yazalım,

$$ \dot{V} = \iiint\limits_V \nabla \cdot \underline{u} \mathrm{d} V $$

Bu formülde hız $\underline{u} = (\dot{x}, \dot{y}, \dot{z})$, çünkü Lorenz sisteminde faz uzayındaki hız budur değil mi? $\underline{u}$'nun uzaklaşımı,

$$ \nabla \cdot \underline{u} = \frac{\partial \dot{x}}{\partial x} + \frac{\partial \dot{y}}{\partial y} + \frac{\partial \dot{z}}{\partial z} $$

Şimdi (6)'daki $\dot{x}, \dot{y}, \dot{z}$'leri bakarak üstteki türevleri hesaplayalım ve formülde yerine koyalım,

$$ = -\sigma -1 - b$$

Hepsi negatif çıktı, ya da $-(\sigma+b+1)$. Bu hesap 1'den küçük olacaktır çünkü $\sigma,b$'nin kesin pozitif oldugunu söylemiştik. Aslında çok iyi bir sonuç bu, bir kere sabit. Bu sabit üçlü entegrali müthiş kolaylaştırır, değil mi, çünkü $\nabla \cdot \underline{u}$ sabit, onun $\mathrm{d} V$ üzerinden entegrali hesaplanırken sabit entegral dışına çıkar, geri kalan sadece $\mathrm{d} V$'nin entegralidir, o da direk $V$ olur, yani hacmin ta kendisi. O zaman

$$ \dot{V} = -(\sigma + b + 1) V$$

Bu sonuç hacimlerin üstel şekilde küçüldüğü anlamına gelir, çünkü

$$ V(t) = V(0) e^{-(\sigma + b + 1)}$$

Lorenz bunu gördü, üstteki sonuç direk onun makalesinden geliyor. Yani elimizde bir başlangıç konum kütlesi var, ama bu kütle, ne olursa olsun, sanki havasını kaybeden bir balon gibi küçülüyor, küçülüyor ve sonunda sıfır hacme iniyor. Bu akılda tutulması gereken kuvvetli bir sonuç. Demek ki tüm gidiş yolları sıfır hacimli bir limit kümesine gitmeye meyilli. Bu küme bir tek nokta, bir çevrim olabilir, ya da bir "garip çekici (strange attractor)" olabilir. Lorenz'in kendisi bu terimi kullanmamıştı, isim sonradan verildi, ama Lorenz'in kullandığı terim de benim çok hoşuma gidiyor, "sonsuz yüzeyler kompleksi". Bugün bu kavram fraktal olarak biliniyor. Neyse, Lorenz bugünkü terimleri kullanmamış olsa da, sisteminde çekicinin bir fraktal yüzey kümesi oldugunu görmüştü. O günlerde bilgisayar grafiklemesi çok ileri değildi, Lorenz bir sanatçıya ne gördüğünü çizdirmeye bile uğraştı, bu konuya sonra geleceğiz. Niye tek yüzey değil, sonsuz kompleks yüzeyi?..

Kalan zamanımda bu limit kümesinin hangi şartlarda nokta oldugunu göstermek istiyorum. Bu pek zor olmayan klasik bir hesap.

Lorenz sistemindeki sabit noktaları bulalım. Cebire girmeyeyim, ama bir tanesinin

$$ (x,y,z) = (0,0,0)$$

olduğu gösterilebilir. Bu sabit nokta her türlü parametre için geçerli. Bu arada sistemin yapısını değiştiren parametre $\sigma,b,r$ demiştik ama bunlardan sadece $r$ o amaçla kullanılıyor, Lorenz $\sigma=10,b=8/3$ ile bunlardan iki tanesini sabitledi, sebepleri [2]'de bulunabilir. Yani klasik parametre denen şey $r$.

Orijin $(0,0,0)$ her $r$ için bir sabit nokta. Fakat orijin stabil değil, su çarkı çerçevesinde bu dönüşün hiç olmadığı durum olurdu.

Bir diğer sabit nokta $x = y = \pm \sqrt{b(r-1)}$, $z=r-1$, eğer $r > 1$ işe, yani bu durumda $r$'nin yeterince büyük olması gerekiyor, aynen daha önce şu çarkı durumunda gördüğümüz gibi, stabil dönüş için $r$'nin yeterince büyük olması gerekiyordu. Dikkat edersek elimizde bir eksi ve artı çift var, Lorenz onlara $C^+$ ve $C^-$ ismi vermiş, herhalde C kullanmasının sebebi taşınım (convection) kelimesiyle alakalı, bu hareket kalıbı kalıcı taşınım ima ediyor.

Ayrıca $r \to 1^+$ iken $C^+$ ve $C^-$'nin yani $x,y,z$'nin sıfıra gittiğini görelim, yani orijinden bir geliş, ona gidiş var, burada bir tür çatallaşma olmalı diye tahmin ediyoruz, ki bu hakikaten doğru, analize devam edince $r=1$ noktasında bir tırmık çatallaşması oldugu bulunabilir. Tırmık süperkritik tırmık, yani sabit noktalar doğduğunda stabil durumdalar.

Orijinin lokal stabilitesi nedir? Orijine yakında $x,y,z$ küçük olacaktır, o zaman karesel terimleri yok sayabiliriz, ve lineerizasyon bize

$$ \dot{x} = \sigma (y-x) $$

$$ \dot{y} = rx - y$$

$$ \dot{z} = -bz $$

verir. Görüldüğü gibi $z$ denklemi diğerlerinden bağlaşımsız hale geldi, ve $z$ üstel bir çürümeye sahip, yani $z(t) \to 0$ gidişi üstel hızda. Yanlız dikkat bunları sistemin geneli için söylemiyorum, bu lineerizasyon, söylenenler orijin etrafında geçerli.

O zaman $z$'ler çürüyor, geriye elimizde $x,y$ bağlamında iki boyutlu ufak bir sistem kalıyor. Bu sistemi ayrı bir şekilde irdeleyebiliriz, matris formunda

$$ \left[\begin{array}{r} \dot{x} \\ \dot{y} \end{array}\right] = \left[\begin{array}{rr} -\sigma & \sigma \\ r & -1 \end{array}\right] \left[\begin{array}{r} x \\ y \end{array}\right] $$

Daha önce öğrendiğimiz iki boyutlu tekniklerle bunun $x,y$ dinamiği için anlamını analiz edebiliriz. İz $\tau = -\sigma - 1 < 0$, determinant $\Delta = \sigma(1-r)$. $r > 1$ ise orijinde bir eğer (saddle) noktası var çünkü determinant negatif. Fakat burada ilginç bir durum var, bu eğer noktası değişik bir tür eğer. Üç boyuttayız, iki boyutta geliş bir boyutta gidiş var.

Devam edelim

$$\tau^2 - 4\Delta = (\sigma+1)^2 - 4\sigma(1-r)$$

$$ = (\sigma-1)^2 + 4\sigma r > 0$$

Yani $\tau^2 - 4\Delta$ her zaman pozitif, eğer $r < 1$ ise o zaman $\Delta$ pozitif, $\tau^2 - 4\Delta$ da pozitif, $\tau$ negatif oldugu için her $x,y,z$ yönünde elimizde bir stabil düğüm (node) var.

Kaynaklar

[1] Strogatz, Video, https://www.youtube.com/watch?v=7iNCfNBEJHo

[2] Lorenz, Deterministic Nonperiodic Flow, http://eaps4.mit.edu/research/Lorenz/Deterministic_63.pdf