Ders 7

Bugünkü ilk konumuz bir önceki işlediğimiz iki boyutlu faz uzaylarının devamı, muhafazakar sistemler. Fakat bu sistemlerin içinde bazı ekler var ki bu ekler bu sistemlerin tipik dinamik sistemlerde görülmeyen çok ilginç bazı sonuçlar sergilemesini sağlıyor.

Tek derece serbestliğe sahip ve Newton Kanunu $F=ma$'yı takip eden bir mekanik sistemi hayal edelim, ama onu şu formda yazıyoruz,

$$ m\ddot{x} = F(x) $$

$m$ kütle, parçacığa etki eden kuvvet (force) $F$ var, ve bu kuvvet parçacığın pozisyonu $x$'e bağlı, bir türev de ekliyoruz,

$$ m\ddot{x} = F(x) = -\frac{dV}{dx} \qquad (1)$$

$V$ potansiyel enerji. Burada farketmemiz gereken $F$'in spesifik şekli, hem $\dot{x}$ hem $t$'ten bağımsız. Fiziksel dilde "sönüm (damping) yok" denebilir, ayrıca sistem dışından etki eden, sistemi "süren" bir şey de yok, gerçi bir sabit üzerinden bunlar olabilir ama zamana bağlı olan bir etki yok.

Bu şartlar ışığında bir şeyler muhafaza edilecek, bu şaşırtıcı değil. Muhafaza edilen enerji, yani kinetik artı potansiyel enerji,

$$ E = \frac{1}{2} m\dot{x}^2 + V(x) $$

muhafaza ediliyor. Bunu görmek için birkaç farklı yol var, eğer elde bir kuvvet formülü var ise ve muhafaza edilen büyüklüğü arıyorsam, iyi bir numara formülün iki tarafını $\dot{x}$ ile çarpmak, ve ortaya çıkan sonuca bakmak. (1)'i tekrar düzenleyelim,

$$ m\ddot{x} + \frac{dV}{dx} = 0$$

$\dot{x}$ ile çarpalım,

$$ m\ddot{x}\dot{x} + \frac{dV}{dx}\dot{x} = 0 $$

Eşitliğin sol tarafına bakalım, ne görüyoruz? Orada mükemmel bir türev sonucu var değil mi?

$$ = \frac{d}{dt} \big( \frac{m\dot{x}^2}{2} + V(x(t)) \big) = 0$$

Zincirleme Kuralının nasıl işlediğini düşünürsek türevin nasıl iki üstteki formüle dönüştüğünü görebiliriz. Dikkat $x$, ya da $\dot{x}$'e göre değil, $t$'ye göre türev alıyoruz. Buna göre $m\dot{x}^2$'nin türevini alınca $2m\dot{x}$ elde ederiz, bir de Zincirleme Kuralından bir $\dot{x}$ daha ortaya çıkar.

Neyse, üstteki türev sıfıra eşit, bu bize o formülün zamandan bağımsız olduğunu söylüyor, yani $E$ sabit. Ya da şöyle söylemek daha iyi: gidiş yolları üzerinde $E$ sabittir, bir dinamik sistemin gidiş yolunu takip ederken, takip ettiğimiz nokta konum uzayında nereye giderse gitsin $E$ fonksiyonunun değeri değişmeyececektir. Bu sürpriz değil, enerjinin muhafaza edildiğini biliyorduk, fakat üstteki de bunu görmenin güzel bir başka yolu.

Daha genel muhafazakar sistemler de var, biyolojide ortaya çıkabiliyorlar, bir örnek soruda bir kağıttan uçağı düşünüyoruz, onu attık diyelim, biraz uçuyor uçuyor sonra bir yere konuyor. Meğer, belli bazı basitleştirici önkoşullar ardından bu sistem de muhafazakar bir sistem. Bu sistemde muhafaza edilen büyüklük enerji gibi kolay irdelenebilen bir büyüklük değil, başka bir şey.

Daha genel olarak muhafazakarlığı belirtmek istersek, $\dot{\underline{x}} = \underline{f} (\underline{x})$ muhafazardır eğer muhafaza edilen bir değer $E(\underline{x})$'e sahipse. $E$ sürekli, reel değerli, ve gidiş yolları üzerinde sabit olan bir fonksiyon olmalı, yani sabitliğin diğer bir ifadesi zamana göre türevin sıfır olması, $\frac{dE}{dt}=0$. Burada ek bir püf nokta; eğer $E$ mesela 17 gibi sadece basit bir sabit sayı olsaydı, üstteki türev yine doğru olurdu; bu tür aşırı basit (trivial) çözümleri de istemiyoruz, yoksa her sistem muhafazakar sistem olur [sebebi alttaki soruyla anlaşılabilir, basit sabitlik çok fazla sistemin muhafazakar olması demektir, bu da istediğimiz türden bir tanım değil], bu sebeple "$E(\underline{x})$'in her açık kümede sabit olmaması" şartını getiriyoruz, bu tanım topoloji, analiz ile alakalı, aşırı detayına burada girmek istemiyorum, ama böylece $E$'nin sabitliğinden kurtuluyoruz.

Soru

Bir muhafazakar sistemin kendine doğru çeken (attracting) sabit noktası olamayacağını göster.

Cevap

Farz edelim ki $x^\ast$ bir kendine çeken sabit nokta. O zaman bu noktaya doğru akan, onun etkisi altındaki noktaların hepsinin aynı enerji $E(x^\ast)$'ye sahip olması gerekir çünkü enerji tüm gidiş yollarında sabit demiştik, ve etki alanındaki tüm noktalar sabit noktaya akıyor. Fakat bu durumda $E(x)$ sabit bir fonksiyon olmalı, çünkü pek çok farklı gidiş yolu üzerinde enerji aynı, ve hepsinin zamana göre türevi sıfır! Bu sonuç muhafazakar sistem tanımımız $E(x)$'in tüm açık kümelerde sabit olmaması şartına ters düşüyor.

Örnek

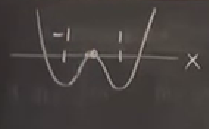
İki kuyulu potansiyel (double-well potential) içinde parçacıkları üzerinden bir örnek görelim [fizikte potansiyelin minimum noktası çevresindeki bölgeye kuyu deniyor, bu örnekte iki tane var]. Şu şekilde bir potansiyel fonksiyon olsun,

$$ V(x) = -\frac{1}{2}x^2 + \frac{1}{4}x^4 $$

Grafiği çizince alttaki gibi bir şekil çıkar, çünkü $-x^2/2$ $x=0$'dan sola doğru o aşağı inen parabolu çizmiş olur, daha büyük $x$'ler için $x^4$ baskın çıkar, ve iki minimum vardır.

$1/2$ ve $1/4$'ü denkleme koydum çünkü üstteki $-1,1$ minimum değerlerinin ortaya çıkmasını istedim. Bu potansiyel fonksiyonu üzerinde "gezinen" bir parçacık her iki minimumun herhangi birinde kalmaktan mutlu olur. Sistemi idare eden denklemler altta, basitleştirme amaçlı olarak $m=1$ alalım (ya da zamanı ölçekleyerek $m$ etkisi $m=1$ olacak şekilde ayarlayabilirdik). Diferansiyel denklemler,

$$ \ddot{x} = -\frac{dV}{dx} = x-x^3 $$

Alın size güzel bir gayrı lineer sistem. Şu anda ikinci derece bir denklem, onu tek dereceli olacak şekilde tekrar yazacağız.

$$\dot{x} = y$$

olarak tanımlayalım, o zaman,

$$\dot{y} = x - x^3$$

olur. 2 boyutlu sistemimiz bu, onu daha önceki derste yaptığımız gibi analiz etmek istiyoruz; sabit noktalarını bulmak, sabit noktalarda Jacobian'ı kullanarak onları sınıflamak amacımız. Jacobian,

$$ \left[\begin{array}{rr} \frac{\partial \dot{x}}{\partial x} & \frac{\partial \dot{x}}{\partial y} \\ \frac{\partial \dot{y}}{\partial x} & \frac{\partial \dot{y}}{\partial y} \end{array}\right] = \left[\begin{array}{cc} 0 & 1 \\ 1-3x^2 & 0 \end{array}\right] $$

Üstteki matrisin sabit noktalardaki değerini istiyoruz. $\dot{x}=0$ demek $x=0$ demektir. İkinci ifadeye bakalım, $x - x^3 = x(1 - x^2)$, bu ifade $x=0$ ya da $x = \pm 1$ olunca sıfırdır. Yani üç tane sabit nokta var,

$(x^\ast,y^\ast) = (0,0)$, o zaman $\left[\begin{array}{rr} 0 & 1 \\ 1 & 0\end{array}\right]$.

$\tau=0$, $\Delta = -1$, yani bir eğer (saddle). Lineerizasyona inanıyoruz, şüpheye gerek yok.

$(x^\ast,y^\ast) = (\pm 1,0)$, o zaman $\left[\begin{array}{rr} 0 & 1 \\ -2 & 0\end{array}\right]$.

$\tau=0$, $\Delta = 2$, demek ki bir merkez var [hoca şimdi alarm zili sesi çıkartıyor]. Hatırlarsak merkezler için lineerizasyona güvenemiyoruz. Fakat birazdan göreceğiz ki eğer ortada muhafaza edilen bir enerji var ise, yani muhafazakar sistem durumunda gayrı lineer sistemde de hakikaten merkez var.

Önce bu sistemde enerjinin ne olduğunu tanımlayalım. Enerji yarı kinetik yarı potansiyel enerjinin toplamı.

$$ E = \frac{1}{2}y^2 - \frac{1}{2}x^2 + \frac{1}{4}x = sabit $$

Enerji gidiş yolları üzerinde sabit. Bu denklem kapalı eğrileri (closed surves) temsil ediyor, bu eğrileri nasıl görebiliriz? Merkezin gerçekten merkez olduğunu görmek için de bu iyi bir yöntem, sarmal yerine kapalı eğriler olacağını görürsek, elimizde bir merkez olduğuna ikna olabiliriz. Faz portresi şöyle,

Orijinde bir sabit nokta var, ve $x=-1,1$'de merkezler.

Orijin yakınında neler olduğunu anlamak için, diyelim ki $x,y$ küçük ise $x^2$'e göre çok küçük kalacak $x^4$ terimi yoksayılır, geri kalanlar $y^2$ eksi $x^2$ eşittir sabit, ki bu hatırlanacağı üzere bir hiperbol (hyperbola) ortaya çıkartır.

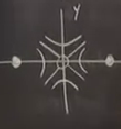
Bu pek şaşırtıcı değil çünkü orijinde bir eğer noktası var. Orijinden çıkan çizgiler üsttekine benzeyecek, "hiperbolik" şeyler bunlar.. Peki okların yönü ne acaba? Bu bilgi için $\dot{x} = y$ formülüne bakmak yeterli, $y$ pozitif olduğu zaman $\dot{x}$ de pozitif. O zaman üstteki grafikte $y$'nin pozitif olduğu üst kısımda eğriler sağa doğru gidecek. Alt bolumde ise tam tersi, sola gidecekler.

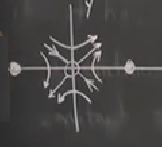
Peki iki yandaki noktalar? Siz de kontrol edebilirsiniz, ama büyük ihtimalle çembersel, kapalı yörüngeler olacaklar. Eliptik te olabilir, kontrol edin. Okların yönü yakınlarındaki oklara bakılırsa alttaki gibi,

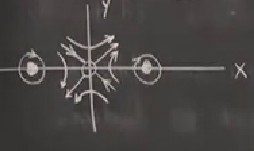
$\dot{y}$'ni nerede sıfır olduğuna bakalım. $\dot{y}$'in sıfır olması sadece yatay gidiş var demektir,

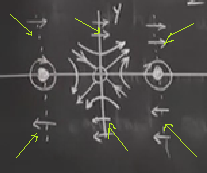
ki $\dot{y}$'in sıfırlık durumu $x=0$ ve $x=\pm 1$'de, üstteki resimde yeşil oklar bu noktalardaki bu yatay gidişi gösteriyor.

Devam edelim, $\dot{x}=0$ olduğu zaman $y=0$ olur, yani $x$ ekseni üzerindeyiz ve buralarda, ve büyük $|x|$ için sağ tarafta eksilik yani aşağı gidiş baskın çıkar, solda yukarı çıkış baskın çıkar.

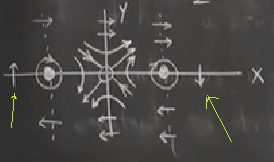
Tüm eğrileri birleştirme zamanı geldi. Denklemdeki simetriye dikkat edelim, $y^2$ ve $x^2$ üzerinden $x$ ve $-x$, $y$ ve $-y$ arasında simetri var, yani resmin üst kısmının alt kısmıyla simetrisi olacaktır.

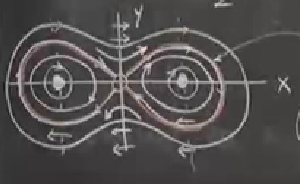
Kırmızı ile işaretlediğim ise homoklinik yörünge (homoclinic orbit). Bu özel bir gidiş yolu. Latince homo aynı, klinik meyil, yani homoklinik bir nokta isek o noktaya tekrar dönmeye meyil, bizim için bu sabit noktada başlayan bir gidiş yolunun tekrar aynı sabit noktaya dönmesi. Tabii bu "kabaca" doğru bir tanım, gerçekte homoklinik yörüngede gidişin aynı sabit noktaya dönmesi sonsuz zaman alıyor. Ayrıca dikkat edersek homoklinik yörünge periyotsal (periodic) değil. Orijinden çıkıp saat yönünden orijine dönüp habire dönüp durmuyoruz. Periyotsal olan diğer gidiş yolları var ama.

Fiziksel olarak bu resim ne söylemeye uğraşıyor?

Bir kapalı yörünge üstte soldaki resimdeki iki nokta arasında habire gidip gelen bir inişi çıkışı temsil ediyor. Enerji ona yetiyor. Daha büyük dışarıda olan gidiş yolları ise üstteki sağ resimdeki iki nokta arasında, daha büyük inişler çıkışlara tekabül ediyor, bunun için enerji daha fazla olmalı çünkü ortadaki ufak tepeyi arada aşmak lazım. Homoklinik yörünge ise aşılamadığı zaman o ortadaki tepeciğin zirvesine yavaş yavaş yaklaşıldığı durum.

Hala eğrilerin kapalı olduğuna inanmıyorsak üç boyutta gösterebileceğimiz enerji yüzeyine (energy surface) bakabiliriz, bu yüzey $E(x,y) = \frac{1}{2}y^2 - \frac{1}{2}x^2 + \frac{1}{4}x^4$ üzerinden çizilebilir. Eksenleri şöyle gösterelim,

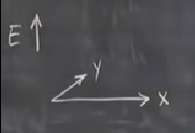
Grafiği çizmeden önce neye benzeyeceğini tarif etmeye uğrasayım; küçükken benim çocuklarımın ilginç pijamaları vardı, pijamalar tek parçaydı, bacaklar, ayakları tamamen kaplıyordu. Bu grafik te ona benzeyecek, aşağı inen iki bölüm olacak, bu bölümlerden en altta öne doğru çıkıntılar olacak [gerçi hocanın birazdan çizeceği şekil direk aşağı gidiyor ama, neyse, belki pijamaların giyilmemiş hali alttaki gibi duruyor].

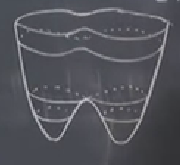
Genel bir yanlışlığa deyineyim, insanlar çoğunlukla gidiş yollarını bu şeklin dış yüzeyinde kafasına göre, herhangi bir yönde hareket eden şekilde hayal etmek istiyorlar. Bu doğru değil. Hatırlarsak gidiş yolları $x,y$ düzleminde yaşıyorlar, ve gidiş belli bir $E$ seviyesine göre. O zaman yüzeyde ama $E$ değişmeyecek şekilde, sanki üstteki üç boyutlu şeklin bir kesit seviyesinde hareket ediyormuş gibi düşünürsek daha iyi.

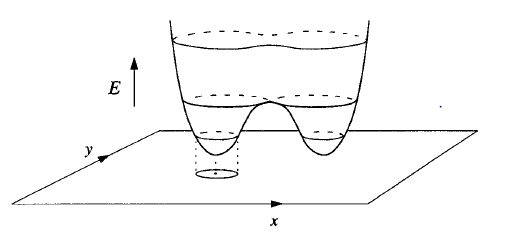
Bunu özellikle söyledim çünkü dört yukarıdaki resimde aşağı iniş, çıkış vardı, o potansiyel fonksiyonunun grafiğiydi, o farklı.

Teori

Muhafazakar sistemler ve 2D gayrı lineer merkezlerininin teorisi şöyle.

Diyelim ki $\dot{\underline{x}}=\underline{f}(\underline{x})$ muhafazakar bir sistem, $\underline{f}$ sürekli ve türevi alınabilir, $\underline{x} \in \mathbb{R}^2$ yani 2 boyutlu düzlem üzerindeyiz. $E(\underline{x})$ muhafaza edilen bir büyüklük. Gerçekten ihtiyacımız olacak bir teknik detay daha, $\underline{x}^\ast$ sadece bir sabit nokta değil, ayrıca izole bir sabit nokta.

İzole derken $\underline{x}^\ast$'in yakınında başka hiçbir sabit nokta olmadığı söyleniyor. Detaylandırmak gerekirse 2 boyutta $\underline{x}^\ast$'e bakıyorum ve onun etrafında $\epsilon$ yarıçapında bir çember çiziyorum, bu çember içinde başka bir sabit nokta yok. İzole noktalar daha yaygın tabii, şimdiye kadar pek çok örnekte onları gördük. İzolasyonun olmadığı bir durum neye benzerdi? Hakikaten olası bir durum mu bu? Bir çizgi, ya da düzlem üzerindeki tüm noktaların sabit nokta olabildiği durumlar var, ama bu durumlar haricinde de izolasyona uymayan örnekler kurgulanabilirdi.

İçinde çok hızlı salınan sinüs fonksiyonu olan bir sistem böyle sabit noktalar ortaya çıkartabilir. $x$'in bir üsteli çarpı $\sin(1/x)$ mesela, bu bir noktaya yaklaşan ve araları sürekli azalan bir seri sabit noktayı üretebilir. Üstte görülüyor, en soldaki noktaya sürekli yaklaşan diğer noktalar.. Bu durumda o en soldaki nokta izole olmaz.

Devam edelim, eğer bu izole sabit nokta fonksiyon $E(\underline{x})$'nin yerel minimum ya da maksimumu ise o zaman $\underline{x}^\ast$ bir merkezdir (yani $\underline{x}^\ast$'a yeterince yakın olan tüm gidiş yolları kapalıdır).

Bu ne demektir? Mesela iki üstteki resmi ele alalım, aşağı inen çukurlardan soldakinin (ki $x,y$ üzerindeki yansıması resimde gösteriliyor) minimum noktasını alırız, ve pat diye bu bir merkez olur.

İspatın ana fikri şöyle: $E$ gidiş yollarında sabit, o zaman gidiş yolları $E$'nin konturlarında yaşıyor olmalı. Yani gidiş yolu bir kesit seviyesi (level set) içinde olmalı. Kesit seviyesinin tamamı olabilir mi? Olabilir, ama bu şart değil.

Konturlar maksimum ya da minimum yakınında kapalı eğrilerdir. Bunu ispatsız veriyoruz ama sezgisel olarak geometrik düşünce yeterli; bir çukuru alalım, onun dip noktası yakını az üstünde çukuru keselim ve bu kesit seviyesine bakalım, orada kapalı bir eğri göreceğiz. Tam ispat için dolaylı (implicit) fonksiyon teorisi gerekli, biz o konulara girmeyeceğiz. Ayrıca, kontur üzerinde bir sabit nokta olup olmadığını nereden biliyoruz? Çünkü izolasyon şartını getirdik, bir sabit nokta yakınında başka sabit nokta olamaz.

Başka bir örneğe geçelim, bu örnek sarkaçları kullanacak.

Problemi genel hatlarıyla anlayabilek için boyutsuz formda yazalım, yani sarkacın boyunu ve yerçekimsel ivmeyi yok sayalım.

$$ \ddot{\theta} + \sin\theta = 0 \qquad (2) $$

Sönüm (damping) ya da dışarıdan ittirme (driving) olmadığını farzediyoruz, yani hala işlediğimiz altyapıyı kullanıyor olacağız.

Diyelim ki $v = \dot{\theta}$. O zaman $\dot{v} = -\sin\theta$.

Enerji fonksiyonu icin (2)'yi $\dot{\theta}$ ile çarparız ve entegre ederiz.

$$ \dot{\theta}(\ddot{\theta} + \sin\theta) = 0 \Rightarrow \frac{1}{2} \dot{\theta}^2 - \cos\theta = sabit $$

Jacobian,

$$ A = \left[\begin{array}{rr} \frac{\partial \dot{\theta}}{\partial \theta} & \frac{\partial \dot{\theta}}{\partial v} \\ \frac{\partial \dot{v}}{\partial \theta} & \frac{\partial \dot{v}}{\partial v} \end{array}\right] = \left[\begin{array}{cc} 0 & 1 \\ -\cos\theta & 0 \end{array}\right] $$

Sabit noktaları düşünelim, $v$ sıfır olmalı, $-\sin\theta$ sıfır olmalı, bu da sadece 0, $\pi$, $2\pi$, .. anlarında, yani $\pi$'nin tamsayı katlarında olabilir.

(0,0) sabit noktasında $A = \left[\begin{array}{rr} 0 & 1 \\ -1 & 0 \end{array}\right]$ verir, $\tau = 0$, $\Delta = 1$. Bu bir lineer merkez.

Muhafazakar sistem demiştik, muhafaza edilen büyüklük $E = \frac{1}{2}v^2 - \cos\theta$. (0,0) noktasında yerel minimum var, o zaman lineer merkez gerçekten bir merkez. Bu fiziksel duruma uyuyor, $\theta=0$ sarkacın tam dik aşağı doğru durduğu hali temsil ediyor, bu tabii ki stabil bir nokta (hiç hareket yok, sarkaç öyle duruyor), bu nokta etrafında ufak salınımlar olabiliyor.

Soru

Sabit nokta (0,0)'in $E$'nin minimumu oldugunu nereden biliyoruz?

Cevap

Enerji fonksiyonu $E$'nin (0,0) etrafında Taylor açılımını yaparım. Önce $\cos\theta$'nin açılımını hatırlayalım,

$$ \cos\theta = 1 - \frac{\theta^2}{2!} + ... $$

O zaman

$$ E = \frac{1}{2}v^2 - [ 1 - \frac{\theta^2}{2} + ... ] $$

$$ = \frac{1}{2} (v^2 + \theta^2) + ... $$

Üstteki sonuca kuşbakışı bir göz atalım.. Bu bir paraboloid değil mi? Ve bu fonksiyonun $v=0,\theta=0$'da minimumu var.

Özetle, muhafazakar sistemlerde merkez bulunca bu adımları takip ediyoruz. Sabit noktaya bakıp onun bir yerel min ya da maks olup olmadığını kontrol ediyoruz. Öyle ise elimizdeki gerçek bir merkez.

Soru

Ya enerji fonksiyonu gerçekten fiziksel bir enerji olmasaydı o zaman muhafaza edilen bir değeri nasıl bulurduk?

Cevap

Evrensel bir yaklaşım var diyemeyeceğim, ama o değeri bulmak için bazı numaralar var. Ödev sorularımızın bazıları bununla ilgili.

Devam edelim, bir diğer sabit nokta $v = 0$, $\theta = \pi$. Bu parametrelerde sarkaç başlangıç noktasından 180 derece yukarıda, tam yukarıda duruyor yani. Doğal olarak bu sabit noktanın stabil olmayacağını bekleyebiliriz (sarkacın dönüp dönüp başlangıçtan tam zıt noktada durması gayet zor).

$(0,\pi)$ için $A = \left[\begin{array}{rr} 0 & 1 \\ 1 & 0\end{array}\right]$, yani bir eyer düğümü var.

Enerji fonksiyonunun şekline bakarak, ya da farklı sabit noktaların yakınında özvektörlere bakarak alttaki gibi bir resme ulaşabiliriz. Zaten biraz önce gördüğümüz paraboloid'den hareketle orijin etrafında konturlar çember olacaktır.

Grafiğin üst sağ çeyreğine bakarsak, orada $v$ pozitif ise, $\dot{\theta}$ pozitif. Oklar çember üzerinde saat yönünde, ya da hep $\theta$'ya doğru. Alt sağ çeyrekte tam tersi, sola gidiş var.

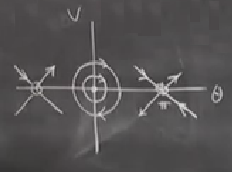
Bu sistemde de bir homoklinik yörünge var. Gerçi hayal etmesi biraz zor ama, diyelim ki sarkaç tam tepe noktada (sabit), ama stabilite yok, oradan azıcık sapınca tekrar aşağı düşüş başlıyor, ve dönüp dönüp tekrar yukarı geliyor ve sonuşur şekilde (asymptotically) oraya yaklaşıyor. Gerçi homoklinik olmak için aynı sabit noktaya dönmek lazım demiştik ama fiziksel olarak yine aynı "duruma" dönüş yapıyoruz. Fakat tam teknik olmak gerekirse, bu bir hetrokliniklik örneği, sabit noktalar değişiyor, bazıları bu duruma "eğer bağlantısı (saddle connection)" ismi veriyor.

Tüm bağlantıları yaparsak,

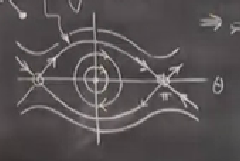
İşte sarkaç problemini böylece çözmüş olduk.

Grafikteki en üst eğriye tekabül eden hareket nedir? Sarkaç sürekli dönüyor. Peki en alt? Sarkaç yine dönüyor ama tam ters yöne doğru. Daha iç kısımdaki çemberlerdeki gidiş yolları ise sarkacın ufak hareketleri, sağa sola salınım var ama büyük hareketler yok. Lise fizik dersinde incelenen hareketler bunlar. Sol ve sağdaki sabit noktalara yaklaştıkça daha büyük hareketler oluyor, heteroklinik yörüngede koca bir tur var, ondan dışarı doğru, ilk başta dediğimiz gibi, habire dönüşler var.

Biraz önce hetro mu, homo mu diye (ufak) bir kararsızlık yaşadık, ama aslında kararsızlığın sebeplerinden biri faz uzayını temsil şeklimizle alakalı. Faz uzayını $v,\theta$ bağlamında bir düzlemde gösterdik, ama bir silindir şeklinde de gösterebilirdik, yani bir düzlemde iki uçta $-\pi$ ve $\pi$ göstereceğimize, o düzlemi alıp katlarız, uçları birleştiririz, bir silindir elde ederiz. Bu silindir aslında sarkaç için en uygun faz uzayı.

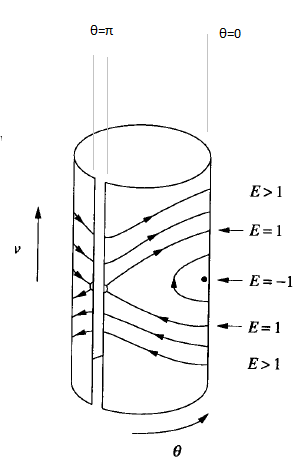
Soru

Hetroklinik yörüngeler için daha belirgin bir örnek var mı?

Cevap

Belki biraz çetrefil olacak ama, bazı problemlerde dalgaları inceliyorsunuz mesela alttaki gibi bir hareket var,

Çözümü dalga fonksiyonu olarak aldığımız bir kısmı diferansiyel denklem (partial differential equation -PDE-) çözümünde, yani çözümde $u(x-ct)$ faraziyesi oluyor, vs. bunu PDE'ye sokuyoruz, çoğunlukla PDE'yi bir ODE haline getirebiliyoruz, ardından dalga çözümlerine bakarken bu çözümlerin bir özelliği oluyor, mesela bir $\xi$ değişkeni üzerinden diyelim, $\xi = \infty$ ve $\xi = -\infty$'da iki düzlük var, yani iki farklı konum var, ve birinden diğerine geçiş.

Belki bu çok çetrefil bir örnek oldu! Ama özetlemek gerekirse, evet, hetroklinik yörüngeler kesinlikle ciddi araştırmalarda kullanılıyor.