Ders 4

Sinek Nüfus Patlaması (Insect Outbreak)

Bu çatallaşma içeren modelin 2 parametresi olacak, ilginç bir özelliği ise sistemin "zıplamalar" içerecek olması; yani dışarıdan değiştirdiğimiz parametre sürekli, ama ona cevaben sistemin davranışı bazen sürekli olmayan şekilde, kesintiler içeren türden, yani değer değişiklikleri "zıplamalar" içeriyor olacak.

Baz alacağımız bilimsel makale [1], makalede işlenen organizma bir tür kurtçuk (spruce budworms). Bu tür kurtçuklar Kanada'da görülüyor en çok, özellikle ormanda çalışan odun üreticileri için bir kabus, eğer bu kurtçuk bir yerde patlama yapmışsa, bir ormanı tamamen yokedebiliyorlar. Ağaç yapraklarını yiyorlar, ve o kadar çok yiyorlar ki (4 sene içinde tüm ormanı bitirebilirler) ormanın gelişmesi sekteye uğruyor. Ormanın tekrar eski haline gelmesi on seneler alıyor.

Bu felaket anlaşıldığı üzere rutin olarak olan bir şey, belki 10-20 sene kurtçuk ortaya çıkmıyor, fakat birdenbire çıkıp çok hasar yaratıyorlar. Pek çok kişi bu durumu nasıl idare edeceklerini düşünmeye başlamışlar, acaba ilaç mı kullansak, ne kadar, ne zaman, kurtçuklar nasıl, ne zaman gelişiyor? Bu soruları [1] cevaplamaya uğraşmış. Çok basit bir modelle ise başlamışlar. Tek bir değişken var, $N(t)$ kurtçuk nüfusu, ve lojistik modeli üzerinden,

$$ \dot{N} = RN \big(1-\frac{N}{K}\big) $$

Lojistik modelinde nüfus kendisiyle yarışır - kurtçuklar yaprakları yemek için kendileri ile yarış halindeler, $K$ taşıma kapasitesi. Diğer yandan bu modelde bir avcı faktörü var, onlar kuşlar. Kuşlar kurtçuk yiyorlar, ve nüfusu eksiltiyorlar, o zaman avcılık (predation) için bir $p$ ekliyoruz,

$$ \dot{N} = RN \big(1-\frac{N}{K}\big) - p(N) $$

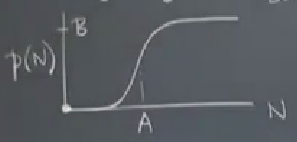
Biyologlar $p(N)$'i şu şekilde tarif ediyorlar, $p(N)$ basit bir fonksiyon değil, yani daha fazla kurtçuk onların daha hızlı ölmesi (yenmesi) anlamına gelmeyecek. Gözlemlerden anlaşılıyor ki kuşlar bu konuda ilginç davranışlar sergiliyor, $p(N)$ gayrı lineer bir fonksiyon. Araştırmalara göre bu fonksiyon,

şeklinde. Çok ufak başlıyor, bu şekilde bir süre gidiyor, sonra birdenbire, bir tipik sayı, $A$ diyelim, sonrası sert bir değişim gösteriyor. Bu bir doygunluk noktası $B$'ye gelinceye kadar devam ediyor. Bunun niye böyle olduğu hakkında biraz daha çetrefil bir hikaye oluşturabiliriz; ilk başta çok az kurtçuk var, kuşlar onları görmüyor bile, bir anlamda kurtçuklar "radarın altında" yaşıyorlar. Fakat bir kritik eşik sonrası kuşlar kurtçukları farkediyor, ve onları avlamaya başlıyor. Belki de kuşların hassas olduğu / baktıkları şey bir yaprak üzerindeki kurtçuk yoğunluğu. Yeterince yoğunluk varsa, kuşlar yaprağa iniş yapıp kurtçukları yemeye başlıyor. Tabii bir süre sonra kuşlar artık yiyebilecekleri kadar hızlı yiyorlar, bundan fazlası mümkün değil, mesela 1 milyon kurtçuk sonrası 2 milyon olabilir, ama onları daha hızlı tüketmek mümkün değil. Bu noktaya da $B$'de ulaşılıyor.

Cebirsel olarak

$$ p(N) = \frac{BN^2}{A^2 + N^2} $$

Soru

Peki kuşların nüfusu avcılıkta önemli değil mi?

Cevap

Tabii bazı faktörleri model dışında bırakıyoruz, kuşların nüfusu bunlardan biri. Ormanın da dinamikleri var, ağaç azaldıkça mesela farklı şeyler olabilir, bu tür faktörleri dışarıda bıraktık. Zaman dilimi burada önemli, üstteki modeli belki de birkaç hafta içinde olanlar üzerinden düşünmek daha uygun, orman, kuşların nüfus dinamikleri çok daha uzun vadeli değişimler. Daha çetrefil, daha uzun vadeli modeller bu ek parametreleri de gözönüne alabilir muhakkak. Ama üstteki modelin de parametre uzayı oldukça geniş / zengin, $R,K,A,B$.

Dört parametremiz var, hepsi birimli, yani boyutsuz değiller. Önceki dersten hatırlarsak modeli boyutsuzlaştırmak, birimi olan parametrelerden kurtulmak belli bir rahatlık sağlıyordu, cebir kolaylaşıyordu, ayrıca modelin özüne inmek te bu şekilde mümkün oluyordu.

Sormak istediğimiz soru şu, belli parametreler çerçevesinde dinamik neye benzer? $R$ büyüyünce kurtçukların büyüme oranı hızlanır mı? $K$ yukarı ya da aşağı inince ne olur? Fakat öyle ki bu tüm dört parametrenin sağladığı tüm olasılıklara bakmaya gerek yok. Önemli olan sadece belli kombinasyonlar. Bu sonucu da boyutsuzlaştırmadan elde edeceğiz. Geniş parametre uzayı olunca bunu otomatik olarak düşünmek iyi olur.

Taktiksel bağlamda boyutsuzlaştırma birkaç değişik şekilde yapılabilir, bunlardan bazılarının analizi diğerlerine göre daha rahattır. Mesela $N$ var, birimi kurtçuk sayısı. İki karakteristik nüfus parametresi var, biri ormanın kurtçuk taşıma kapasitesi $K$, diğeri $A$ ki bu nokta sonrası avcılık hızla artıyor. $N$'i $A$ ile mi bölsek, yoksa $K$ ile mi? İkisi de mantıklı olurdu.

Şimdi $N$'in ölçeğini yarı tahminsel (heuristic) olarak seçelim. Öyle seçelim ki gayrı lineer $p(N)$'in hiç parametresi olmasın. Bunun için $x = N / A$ tanımlayalım, ve herşeyi $x$ bazlı olacak şekilde değiştirelim.

$$ N = Ax $$

$$ \dot{N} = A \dot{x}$$

$$ A \frac{dx}{dt} = R A x \big(1 - \frac{Ax}{K} \big) - \frac{BA^2x^2}{A^2(1+x^2)} $$

Şimdi, demiştik ki eksiden sonra gelen nüfustan eksilten gayrı lineer "avcılık teriminin" hiç parametresi olmasın. Sebebinin birazdan anlayacağız. İlk önce $A^2$'ler iptal oluyor. Sonra herşeyi $B$'ye bölebiliriz.

$$ \frac{A}{B}\frac{dx}{dt} = \frac{RAx}{B} \bigg( 1 - \frac{A}{K}x \bigg) - \frac{x^2}{1+x^2} $$

Bu birimsiz bir denklem artık, değil mi? Tabii $x$ birimsiz, onun bağlı olduğu $t$ var, ve onun birimi hala var, gün, hafta, vs. Eğer birimsiz zaman elde etmek isteseydik, onu nasıl yapacağımızı görüyoruz,

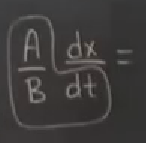
Üstteki formülün sol kısmı bu, ve birimsiz zaman

$$ \tau = \frac{Bt}{A} $$

olur. Bu arada birimsiz bir grup daha var, mesela $A/K$. Tüm bu seçimleri yaptıktan sonra, bakalım sistemimiz neye benzeyecek, birimsiz zamana göre olan türevi temsil etmek için $\dot{x}$ yerine $x'$, $A/K$ yerine $1/k$ , $RA/B$ yerine $r$ kullanalım, son ikisi birimsiz büyüme hızı, birimsiz taşıma kapasitesi olacak. Tanıdık sembolleri kullanmaya uğraşıyorum, bu problem üzerinde düşünmemi kolaylaştırıyor, lojistik modelde $K,R$ görmeye alışığım, onların küçük harfli halini kullanmak uygun olur.

$$ x' = rx \bigg( 1 - \frac{x}{k}\bigg) - \frac{x^2}{1+x^2} $$

Evet, daha önce reklamını yaptığımız gibi 4 parametre gitti, 2 parametre kaldı. Bir şekilde dört parametreyi iki tane içine kattık, böylece geriye en öz parametreler kaldı.

Birimsizleştirmeyi anlamak için şu örneği de aklımızda tutalım; Holywood filmlerinde mesela dalgalar içinde sallanan bir gemi görüyor olabiliriz, ama o sahne çoğunlukla ufak maket modellerle bir stüdyoda çekilmiştir, eğer herşey düzgün şekilde ölçeklenirse bu ufak modelin büyük modelden orantısal olarak hiçbir farkı yoktur. Burada yaptığımız bir anlamda budur.

Dikkat edersek son eriştiğimiz model tek boyutlu tek çizgi üzerinde akış (flow) artık. $x^\ast=0$ olunca $x'=0$. Bu bariz bir sabit nokta, başta hiç kurtçuk yoksa ondan sonra da hiç yok. Bir diğeri için iki tarafı $x$ ile bölüyoruz, % $$ r \bigg(1-\frac{x}{k}\bigg) = \frac{x}{1+x^2} $$

Bu denkleme bir süre odaklanmak istiyorum şimdi; bu denklem ölçeklemeyi niye yaptığımızı sergileyen güzel bir örnek. Niye parametreleri avcılık teriminden çıkarttım ve lojistik terim içine kattım? İşte yapmamın sebebi yukarıda görülüyor, parantez içindeki gayet rahat anlaşılan bir ifade, bir düz çizgi formülü. $r,k$'yi değiştirdikçe bu değişim bir düz çizginin kesisine, ya da eğimine yansıyacak. Ama parametreler eşitliğin sağ tarafındaki gayrı lineer kısımda olsaydı, bu ayarlamaları gözlemek daha zor olacaktı.

Analiz edelim. Bu arada niye direk çözmüyorum bu denklemi, eşitliğin sağının bölenindeki ifadeyle iki tarafı çarpsam bir $x$ bazında küpsel denklem elde ederdim. O denklemi bir bilgisayar yazılımına girebilirdim, üç tane kökü elde ederdim, ama sonra kendi kafamı bir güzel karıştırmış olurdum, çünkü küpsel formül arap saçı gibi karmakarışık bir şey olurdu. Ne dediğini anlamak çok zor olacaktı. Bu doğru bir düşünce şekli değil. Biz grafiksel yaklaşacağız.

Denklemin sağ kısmını düşünürsek, ufak $x$ için $x$ gibi gider, büyük $x$ için $1/x$ gibi davranmaya başlar, iki yandan

Birleştirelim, ve çizgiyi çizelim,

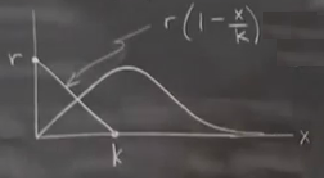
Grafiksel şekilde yaklaşmanın esas ödülünü $r,k$'yi değiştirmeye başladığımızda elde ederiz. Eğer küpsel denklemi çözmeye uğraşsak üç tane sıfır da elde edebilirdik, ama şu anda sadece bir sıfır var. Üç tane kök demiştik, $r,k$ değişimi üzerinden farklı bir resim ile üç kök $a,b,c$ elde edebiliriz,

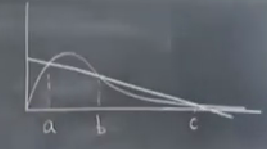
Kurtçuk sayısı bağlamında $a$ civarı az var, orta seviye $b$, $c$ seviyesinde artık patlama yaşanıyor, bu kurtçuk istilası.

Pek çok $r,k$ kombinasyonunu düşünmek için şu resme bakalım,

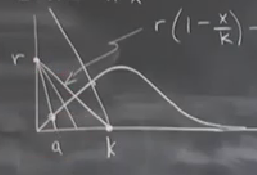
$r,k$ ne olursa olsun mutlaka bir kök oluyor (çizgi eğriyi bir yerde muhakkak kesiyor). İki üstteki resimde çok büyük $k$ olunca üç tane kök elde edebiliyoruz. Anlamak istediğimiz bu geçişler, tek kökten üç'e nasıl gidildiği.

Şimdi büyük $k$ değerleri için ne olduğuna bakalım. Üstteki resmi tekrar çizelim,

Eğer küçük $r$ sonucu eğimi az olan bir çizgi varsa, tek bir kesişim noktası var. Şimdi diyelim ki sistemin bir düğmesi, kontrolü üzerinden $r$'yi yavaş yavaş arttırıyorum. Bir noktada çizgi eğriye teğet hale gelecek. O kesişmeye kadar $r$'de niceliksel değişim var ama niteliksel bir değişim yok. İlginç bir şey olmuyor. İlk ilginç niteliksel durum teğetlik anı.

Ve daha önceki derslerden öğrendiğimiz gibi bu teğet anları bir çatallaşmanın oluştuğuna dair bir işaret. Çizgiyi biraz daha arttırınca iki tane kesişim noktası ortaya çıkıyor, sanki $b,c$ birbirinden ayrılıp iki ayrı nokta haline geliyorlar. O noktada eğri çatallaşması var. İki kesişimden sonraki ilginçlik tek nokta kesişimi, orada da eğer çatallaşması var. Daha da üste çıkınca artık eğri kesişimi yok, sadece $c$ var. Kritik olaylar aslında $b$'de oluyor denebilir; o nokta eğer çatallaşması bağlamında ya $a$ ya da $c$ ile çarpışıyor / birleşiyor.

Bu oldukça çetrefil bir olaylar zinciri; özet olarak göstermek için $r,k$ diyagramı faydalı olabilir. Bu diyagramda nerede bir, nerede iki, üç kök olduğunu gösterebiliriz.

İki eğri bir noktada birleşiyorlar, bu noktada eğriler kesişiyorlar, hatta teğetsel olarak kesişiyorlar. Resimde gösterilen bölgede üç tane sabit nokta var. Bunu derken $x^\ast=0$'da her zaman olan bariz / basit sabit noktadan bahsetmiyorum, bariz olmayan ve iki üstteki resimde yaptığımız değişimlerden elde edeceğimiz üç noktada bahsediyorum. Eğriler üzerinde ise sabit noktalar iki tane.

Sabit noktaların stabilitesine bakalım şimdi; daha önce sorduğumuz sorunun cevabını da arıyoruz ayrıca, $c$ noktasının istila noktası olduğunu nasıl anlayacağım?

Diyelim ki elimizde 3 sabit nokta olduğu haldeyiz ($x^\ast=0$ haricinde), ve kurtçukların artış oranı boyutsuz değişken $x'$'e bakıyoruz, ve bildiğimiz grafiğimizi çizecegiz birazdan. Ama önceki ifadeye bir daha bakalım,

$$ x' = rx \bigg( 1 - \frac{x}{k}\bigg) - \frac{x^2}{1+x^2} $$

Eğer $x$ sıfıra yakınsa parantez içi 1'e yakın, sol taraf $rx$ (neredeyse) haline gelir, sağdaki kısımdaki bölüm çok ufaktır çünkü $x$'in karesel bir ifadesi, bu sebeple sağ kısım dikkate alınmayabilir. Yani sonuç olarak bu ifadenin $x=0$ etrafındaki lineerizasyonu $rx$'tir.

Ve $rx$, ufak nüfus değerleri için üstel artış var demektir, bu mantıklı çünkü ufak nüfusta demiştik ki kuşlar onları görmüyorlar, bu noktada büyüyebildikleri kadar hızlı büyüyorlar, nüfusun tipik artışı üsteldir. Grafiği şöyle çizebilirim,

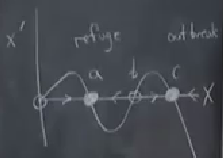
Sabit noktalarda stabilite sürekli değişiyor. Bu topolojik olarak doğru mu? Tek çizgi üzerinde yanyana iki tane stabil sabit nokta olması mümkün değildir. Yani okları nasıl çizerdik?

Bu anlamsız bir resim.

İki üstteki resimde $c$ nüfus patlaması (outbreak), $a$ ise saklanma (refuge) noktası. Eşik değeri $b$, eğer $b$'den fazla kurtçuk var ise büyümeye devam edip $c$'ye erişirler. Ama $b$'den az kurtçuk var ise azalıp $a$ seviyesine düşüyorlar.

Zıplama fenomeni bir eyer düğümü çatallaşması ardından ortaya çıkar. Diyelim ki $x$ değişkeni $a$ noktasında ve herhangi bir sebepten dolayı parametrelerde bir kayma olmaya başlıyor. Orman yaşlandıkça ve içindeki ağaçlar büyüdükçe daha fazla yaprağa sahip olacaklar. [1]'e göre bu $a$'nin yavaşça büyümesi demektir. Niye? Hatırlarsak $r = RA / B$, büyük $A$'yi hatırlarsak bu kuşların kurtçukları farketmeye başladığı kritik seviye idi. [1] diyor ki $A$ tüm ormanın büyüklüğüne orantılıdır, yani eğer yaprak başı kritik kurtçuk yoğunluğu $A'$ dersek (türev değil), ve $S$ ormandaki tüm yaprak sayısı, $A' S$ bize $A$'yi verir. O zaman $S$ yavaşça büyüyecek (orman büyüyor), bu $A$'yi yavaşça büyütecek, ve sırasıyla $r$ formülü üzerinden $r$ değişecek.

Bu değişimin sabit noktaları nasıl etkileyeceğini düşünelim, üstteki resimde düz çizgi yavaş yavaş yukarı çıkıyor,

Sabit noktalar $a,b$ birbirine yaklaşıyor, teğetlik olmadığı durumda (kesikli çizgiler) $a,b$ yok ama, ama tabii en sağda hala $c$'den geçiş var.

Bu resmin anlamı ne? Eğri yukarı çıktıkça belli bir $r$ ardından $a$ olmayacak, sistemin $c$ sabit noktasına "zıplamaktan" başka çaresi yoktur. Zıplama derken bunu kastediyordum.

Histeresis (Hysteresis)

Bir parametreyi değiştirip $a$'dan $c$'ye zıplama ardından parametrenin geri eski değerine döndürülmesinin sistemi $a$'ya döndürmemesine histeresis deniyor. Pek çok gayrı lineer sistemlerde bu tür "geri dönülmezlik" vardır. Mesela bir ormancılık kanunu geçti, bunun yan etkisi olarak kurtçuklar patlama yaptı, $c$'ye gelindi. Çevreciler protesto etti, eski hale dönelim dediler, fakat $r$'yi eski seviyesine getirmek bizi eski duruma döndürmez.

Zihinde canlandırmak için su resmi düşünelim,

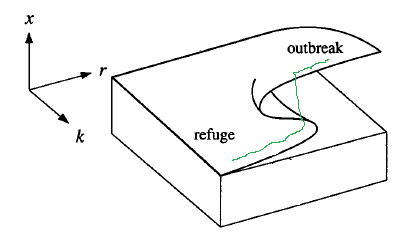
Yeşil çizgi soldan sağa doğru $r$'nin değişimi. Zıplama sonrası alttan üstteki kavisli yüzeye geliniyor, ama bu noktada "geriye gitmek" demek aynı yüzey üzerinde sola gitmek demektir. Geriye gitmek için o yüzeyde sola, aşağı, sağa, sonra tekrar sola gitmek lazım.

Ek Bölüm

Çember Üzerinde Akış

Şimdiye kadar $\dot{x} = f(x)$ formülüne odaklandık, ve bu formülü bir çizgi üzerindeki vektör alanı olarak hayal ettik. Şimdi yeni bir diferansiyel denklem ve onun faz uzayına bakma zamanı geldi; Alttaki formül

$$ \dot{\theta} = f(\theta) $$

bir çember üzerindeki vektör alanını temsil ediyor. Bu sistemde $\theta$ çember üzerindeki bir nokta, ve $\dot{\theta}$ o noktadaki hız vektörü, ki bu vektör $\dot{\theta} = f(\theta)$ ile kararlaştırılıyor. Aynen çizgi durumunda olduğu gibi çember de tek boyutlu, fakat ek bir özelliği daha var, bir yöne sürekli akarak başladığı noktaya dönmesi mümkün.

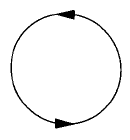
Böylece derste ikinci kez periyodik çözümlerin mümkün olduğunu görüyoruz. Başka bir şekilde söylemek gerekirse çember üzerindeki vektör alanları salınım halineki sistemlerin en baz halini temsil ediyor.

Birörnek Titreşir (Uniform Oscillator)

Çember üzerindeki bir noktaya çoğunlukla bir açı ya da bir faz adı verilir. O zaman dünyanın en basit titreşiri

$$ \dot{\theta} = \omega $$

ki $\omega$ bir sabit olmak üzere. Bu sistemin çözümü

$$ \theta(t) = \omega t + \theta_0 $$

Bu çözüm çember etrafındaki açısal frekans $\omega$ ile yapılan birörnek hareketi temsil eder. Bu çözüm periyotsal yani $\theta(t)$, $2\pi$ kadar değişince baştaki yerine dönmüş oluyor, $T = 2\pi/\omega$ zaman sonra. $T$'ye salınımın periyotu diyoruz.

Dikkat edersek salınımın genliği hakkında hiçbir şey söylemedim. Sistemizde hakikaten genlik yok, eğer olsaydı o zaman 2 boyutlu bir faz uzayı elde ederdik.

Birörnek Olmayan Titreşirler

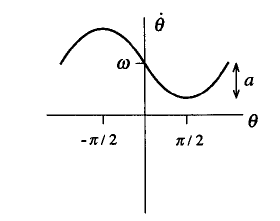
$$ \dot{\theta} = \omega - a\sin\theta $$

pek çok mühendislik / bilim dalında ortaya çıkar: elektronik, biyoloji, mekanik. $f(\theta) = \omega - a\sin\theta$'nin tipik grafiği şöyledir,

Ateş Böcekleri (Fireflies)

Senkronizasyonun doğada görülebilen en müthiş örneği herhalde ateş böceklerinin senkronize olması. Güney Doğu Asya'nın bazı bölgelerinde binlerce erkek ateş böceği gece vakti ağaçlarda toparlanıp senkronize bir şekilde bir ışık verip ışık kapatırlar, dişi ateş böcekleri yukarıda uçarak aşağı bakarak kendilerine uygun "yakışıklı" bir ışık ararlar.

Peki bu ışık yanıp sönmesi (flaş diyelim) nasıl senkronize olur? Muhakkak ateş böcekleri senkronize bir şekilde başlamazlar, güneş batmaya başlarken birer ikişer mekana gelirler, ve senkronizasyon yavaş yavaş ortaya çıkar. Kilit gözlem şudur: ateş böcekleri birbirlerini etkilerler. Bir ateş böceği diğerinin yanıp sönmesini görünce kendi ışıldamasını ya yavaşlatır ya da hızlandırır ki bir sonraki çevrimde aşağı yukarı aynı fazda yanıp sönebilsin. İşin ilginç tarafı tabii ki iki, birkaç ateş böceği arasındaki lokal bir uyumlanmanın bir süre sonra tüm böceklerde görülmesi.

Model

Diyelim ki $\theta(t)$ ateş böceğinin flaş ritminin fazı, ve $\theta=0$ bir flaşın verildiği ana tekabül ediyor. Diyelim ki etrafta başka bir etki yok, ateş böceği $\omega$ frekansında normal flaşını veriyor, yani $\theta = \omega$.

Şimdi dışarıdan

$$\Theta = \Omega \qquad (1)$$

fazında ile başka etkileyici bir flaşın görüldüğünü farzedelim, ki $\Theta=0$ o diğer flaşın verildiği anı temsil ediyor. Modelimize göre eğer bu etki eğer çevrim içinde daha önde ise etkilenen böcek kendi flaşını hızlandırıp senkronize olmaya uğraşacak, ya da geride ise yavaşlayıp yine uyumlanmaya çabalayacak. Bu durumu

$$ \dot{\theta} = \omega + A \sin(\Theta - \theta) \qquad (2) $$

ile modelleyebiliriz, ki $A > 0$. Mesela eğer $\Theta$, $\theta$'nin ilerisinde ise, $0 < \Theta - \theta < \pi$ gibi, o zaman ateş böceği hızlanacak ($\dot{\theta} > \omega$). Uyumlanma gücü $A$ böceğin kendi frekansını ne oranda değiştirebildiğini ölçüyor.

Uyumlanmanın olup olmadığını görmek için faz farkı $\phi = \Theta - \theta$'nin dinamiklerine bakalım. (1)'den (2)'yi çıkartırsak,

$$ \dot{\phi} = \dot{\Theta} - \dot{\theta} = \Omega - \omega - A\sin\phi \qquad (3) $$

Denklem $\phi(t)$ birörnek olmayan titreşir denklemidir. Üstteki denklemi birimsiz hale getirmek mümkün,

$$ \tau = At, \quad \mu = \frac{\Omega - \omega}{A} $$

O zaman

$$ \phi' = \mu - \sin\phi $$

ki $\phi' = \mathrm{d}\phi/\mathrm{d}\tau$. Boyutsuz grup $\mu$ uyumlanma gücüne kıyasla frekans farkının bir ölçüsü. $\mu$ ufak olduğu zaman frekanslar nispeten birbirlerine yakın, ve uyumlanma olabileceğini beklememiz lazım. Bu alttaki grafikte doğrulanıyor, grafikte (1) için farklı $\mu \ge 0$ için vektör alanları çizilmiştir ($\mu < 0$ durumu benzer)

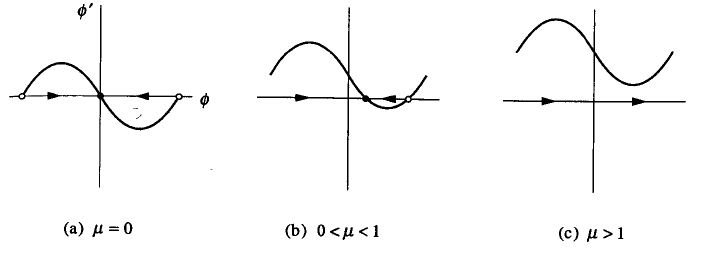
$\mu=0$ olduğu zaman tüm gidiş yolları stabil sabit nokta $\phi^\ast=0$'a doğru akıyor, üstteki figürde (a) durumu. Bu durumda ateş böceği $\Omega=\omega$ durumunda arada sıfır faz farkı olacak şekilde uyumlanır. Yani diğer böcek ve uyumlanan ateş böceği, uyumlanan böcek kendi frekansında etkilendiğinde, {\em tam uyum} halinde aynı anda yanıp sönmeye başlayacaklardır.

(b) figüründe $0 < \mu < 1$ için (a)'daki eğri yukarı çıkar, ve stabil ve gayrı-stabil sabit noktalar birbirine yaklaşır. Tüm gidiş yolları hala stabil bir noktaya doğru çekilirler, ama şimdi $\phi^\ast>0$. Faz farkı bir sabite yaklaştığı için bu duruma ateş böceği ritminin etkileyiciye {\em fazsal kitlenmiş olduğu} adı verilir.

Faz kitlenmesi, etkileyen ve etkilenen böceğin aynı anlık frekansta flaşladığıdır, ama artık aynı anda flaşlamazlar. $\phi^\ast>0$ sonucu etkileyenin her çevrimde böcekten daha ileride (önce) flaşladığını anlamına gelir. Bu mantıklı herhalde, $\mu>0$ farzettik, ki bu $\Omega > \omega$ demektir, etkileyen etkilenenden daha hızlı, ve böceği gitmek istediğinden daha hızlı şekilde etkiliyor. Diğer böcek bu sebeple geriye düşüyor. Fakat etkileyen ötekine kat kat tur farkı atmıyor, diğeri her zaman sabit bir $\phi^\ast$ kadar geride.

Eğer $\mu$'yu arttırmaya devam edersek stabil ve gayrı-stabil sabit noktalar sonunda biraraya gelip $\mu=1$'de bir eyer düğüm çatallaşması ortaya çıkartacaklar. $\mu>1$ için her iki sabit nokta yokolur, ve faz kitlenmesi ortadan kaybolur; faz farkı $\phi$ sürekli bir şekilde artacaktır, bu duruma faz kayışı adı verilir, figürde (c) durumu (tabii faz farkı $\pi$'ye gelince titreşirler tekrar aynı fazdadır). Dikkat edelim fazlar birbirinden birörnek orada ayrılmıyor, $\phi$ (c) figüründe $\phi=\pi/2$'de sinüs dalgasının minimumu altından geçerken en yavaş halde artıyor, ve en hızlı şekilde $\phi=-\pi/2$ iken artıyor.

Bu model bazı spesifik ve test edilebilecek öngörüler yapıyor. Uyumlanmanın sadece etkileme frekanslarının simetrik bir aralığında mümkün olacağını öngörüyor mesela, spesifik olarak $\omega - A \le \Omega \le w + A$. Bu aralığa uyumlanma bölgesi deniyor.

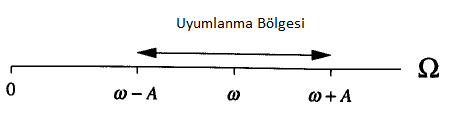
Bu bölgenin büyüklüğünü deneysel olarak ölçersek $A$ parametre değerini de hesaplayabiliriz. O zaman model uyum sırasındaki faz farkı için nihai bir öngörüde bulunur,

$$ \sin\phi^\ast = \frac{\Omega-\omega}{A} $$

ki $-\pi/2 \le \phi^\ast \le \pi/2$ (3)'un stabil sabit noktasına tekabül ediyor.

Dahası da var; $\mu > 1$ için faz kayışının periyotu şu şekilde tahmin edilebiliyor. $\phi$'nin $\pi$ kadar değişmesi için gereken zaman

$$ T_{kayış} = \int \mathrm{d} t = \int_{0}^{2\pi} \frac{\mathrm{d} t}{\mathrm{d} \phi} \mathrm{d} \phi $$

$$ = \int_{0}^{2\pi} \frac{\mathrm{d} \phi}{\Omega - \omega - A\sin\phi} $$

Bu entegrali hesaplamak için kitabım [2]'nin 4.3 bölümündeki tekniği kullanırız,

$$ T_{kayış} = \frac{2\pi}{\sqrt{(\Omega-\omega)^2} - A^2} $$

$A,\omega$ ateş böceğinin doğasından gelen değişmeyen şeylere bağlı olduğunu farzettiğimize göre üstteki iki denklemin tahminleri etkileyen frekans $\Omega$ değiştirilerek test edilebilir. Bu deneyler halen yapılmadı.

Kaynaklar

[1] Ludwig et al, Quantitative Analysis of Insect Outbreak Systems, J. Animal Ecology, 1978

[2] Strogatz, Non-Linear Dynamics and Chaos