Ders 2

Önceki derste $\dot{x} = f(x), \quad x \in \mathbb{R}$ türünden sistemlere baktık, dedik ki bu tür sistemleri analitik olarak çözmeye uğraşabilirsiniz, fakat çoğunlukla / eğer $f$ gayrı lineer bir fonksiyon ise, ortaya çıkacak entegralleri analitik olarak, değişkenlerin ayrılması tekniğiyle mesela çözmek imkansız olabilir. Diğer taraftan bu çerçevede çizim kullanmak daha kolay, bu derste kullanacağımız yaklaşım da bu olacak.

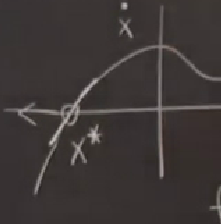
Örnek üzerinde görelim; mesela alttaki gibi berbat (!) bir $f$ var.

Çözmek için x ekseninde zamana göre hareket eden bir parcaçık hayal ederiz, o parcaçığın hızı $\dot{x}$ olacaktır, yani bu hız parcaçığın x ekseninde nerede olduğunu göre değişecek, ve tabii ki bu hız parcaçığın yerini değiştirecektir, sonra gelinen yerde yeni bir hız olacaktır, vs.. Aslında üstteki örnekte çizilen parcaçık hep sağa gidecek, tabii eğer $f$'in x eksenini kestiği noktanın solunda değil ise. O zaman da hep sola giderdi.. Bir de o kesişim noktasında bir stabil nokta var, onu unutmayalım, çünkü o noktadan başlarsam hiçbir yere hareket etmem ($\dot{x}=0$).

Çoğunlukla çizim yapacağız dedik, fakat bir analitik teknik var ki kullanması kolay ve oldukça faydalı, tekniğin ismi sabit bir nokta etrafında lineerleştirme (linearization around a fixed point). Bu teknikle bir sabit nokta $x^\ast$ etrafındaki (üst yıldız notasyonunu sabit noktalar için kullanıyorduk hatırlarsak) dinamiği incelemek istiyoruz, ki sabit noktalar $f(x^\ast)=0$ şartını yerine getirecek noktalar, çünkü o noktalarda hız sıfır. Lineerleştirmeye göre bu noktanın "yakın komşularına" bakarız, hemen etrafına yani, ve eğer o noktalarda hız artıp bizi noktadan uzaklaşırıyorsa bir büyüme vardır, eğer azalma var ise tekrar sabit noktaya döneceğiz demektir, bir çürüme (decay) vardır. Tekniği şöyle kullanırız, diyelim ki

$$ x(t) = x^\ast + \eta(t), \qquad |\eta| << 1 $$

olsun, $\eta$ bir çürüme terimi, ve onun büyüklüğünün, yani mutlak değerinin çok küçük olacağını farz ettik ($a<<b$ sembolü $a$ değeri $b$'den çok küçüktür demek), çok küçüklüğü birazdan daha iyi açıklayacağım. Neyse amacım $\eta$ için bir denklem türetmek ki böylece büyüyor mu çürüyor mu onu görebileyim. Üstteki $x$'ten hareketle $\dot{x}$ nedir?

$$ \dot{x} = \frac{d}{dt}( x^\ast + \eta \big) = \big( x^\ast + \eta \big)^{.} = \dot{\eta} $$

Eşitliğin en sağı ortaya çıktı çünkü sabit noktada değişim sıfır demiştik, $\dot{x^\ast} = 0$, geriye sadece $\dot{\eta}$ kaldı. Diğer yandan $\dot{x}=f(x)$ olduğu için

$$ \dot{x} = \dot{\eta} = f(x) = f(x^\ast + \eta) $$

Fakat hala tam ne olduğunu göremiyoruz çünkü $f$ karmaşık bir fonksiyon. Bu noktada lineerleştirmeyi devreye sokuyoruz, diyoruz ki $f$ yeteri kadar pürüzsüzdür (smooth) yani herhangi bir $x$ etrafında Taylor serisi yaklaşıklaması yapabilirim.

$$ f(x^\ast + \eta) = f(x^\ast) + \eta f'(x^\ast) + \frac{\eta^2}{2}f"(x^\ast) + ... $$

Tabii lineerleştirmeyi herhangi bir nokta etrafında değil sabit nokta etrafında yapıyoruz, o zaman $f(x^\ast)=0$ olduğu için

$$ f(x^\ast + \eta) = \cancelto{0}{f(x^\ast)} + \eta f'(x^\ast) + \frac{\eta^2}{2}f"(x^\ast) + ... $$

$$ f(x^\ast + \eta) = \eta f'(x^\ast) + \frac{\eta^2}{2}f"(x^\ast) + ...$$

Geri kalan formül $\eta$'ya lineer olarak bağlı. Ama hala $f'(x^\ast)$ var? $\eta$'nin çarptığı ibare çetrefilmiş gibi duruyor, ama unutmayalım, o ifade bir tek sayı aslında çünkü fonksiyona bir sabit nokta değeri geçiyoruz, ve bir sayı elde ediyoruz. $f'(x^\ast)$ sonuçta $f$'in türevinin $x^\ast$ noktasındaki değeri değil midir? Yani $f$'in sabit noktadaki eğiminden (slope) bahsediyoruz.

Sonuç olarak elimde eşitliğin sağında bir sayı çarpı $\eta$, bir diğer sayı çarpı $\eta^2$ var. Matematikte bu tür argümanı daha önce görmüş olabiliriz, $\eta$ 1'den çok küçüktür demiştik, o zaman 1'den çok küçük bir şeyin karesi daha da küçük olacağına göre $\eta^2$'den başlayarak sağa giden tüm terimleri atabiliriz. Lineerleşirmenin arkasında yatan fikir bu, karesel terimlerden (quadratic term) kurtulmak.

Fakat kendimize bir daha soralım, $\eta^2$'li terimi $\eta$'li terimle kıyaslayarak düşünürsem, atılabileceğinden emin miyim? Evet, eğer $f'(x^\ast)$ sıfır değil ise. Çünkü eğer o ilk terim sıfır olursa yokolur, ve geri kalan tek önemli terim $\eta^2$'li terim olur, bu durumda ikinci terimi yok kabul edemezdik. Matematiksel olarak derli toplu bunu bir daha ifade edersek, eğer $f'(x^\ast) \ne 0$ ise, ufak $\eta$ için $|f'(x^\ast) \eta| >> |\frac{\eta^2}{2} f"(x^\ast)|$.

Yani $O(\eta^2)$ ifadelerini formülden atarız ($O()$ notasyonu derece (order of) demektir, yani iki ve daha büyük dereceli terimlerden bahsediyoruz),

$$ f(x^\ast + \eta) = \eta f'(x^\ast) + \cancel{\frac{\eta^2}{2}f"(x^\ast)} + \cancel{...}$$

$$ f(x^\ast + \eta) = \eta f'(x^\ast) $$

Daha önce demiştik ki $\dot{\eta} = f(x^\ast + \eta)$, o zaman $x^\ast$ noktasında,

$$\dot{\eta} = r \cdot \eta$$

lineerizasyonunu elde ediyoruz ki $r=f'(x^\ast)$. $\dot{\eta} = r \cdot \eta$ sonucu güzel bir sonuç, çünkü bu ifade özünde basit bir lineer diferansiyel denklem, ODE dersinden bize tanıdık gelen bir ifade, $r$'nin pozitif ya da negatif olmasına bağlı olarak ya büyüme ya da çürüme ortaya çıkacak. Çözüm,

$$ \eta = \eta_0 e ^{rt} $$

ki bu çözüm $r > 0$ ise büyür, $r < 0$ ise çürür. Üstteki grafikte görüyoruz ki eğim yani $f'(x^\ast)$ sıfırdan büyük o zaman sabit nokta olduğu stabil olmalı, ki hakikaten de böyle. Lineerizasyon tek boyutta böyle. İki ya da daha fazla boyutta da lineerizasyon kullanacağız.

Peki ya daha önce koyduğumuz şart $f'(x^\ast) \ne 0$ doğru değil ise ne olur? o zaman lineerizasyondan hiçbir bilgi elde edemiyoruz, yani bu teknik ise yaramıyor. Nokta stabil olabilir, yarı stabil olabilir, ya da her iki durumun bir karışımı karma bir durum olan yarı-stabilite olabilir. Dört örnek vermek gerekirse,

$$ \dot{x} = x^2, \qquad \dot{x} = -x^2 $$

$$ \dot{x} = x^3, \qquad \dot{x} = -x^3 $$

sistemlerini düşünelim. $x^\ast=0$ hepsi için bir sabit nokta. Bunu görmek kolay herhalde, eşitliğin sağ tarafına sıfır verince hepsi $\dot{x} = 0$. Şimdi $f'(x^\ast)$ şartını kontrol edersek, hepsi için $f'(x^\ast) = f'(0) = 0$. Teker teker neler olduğuna bakalım şimdi, mesela $\dot{x} = x^2$,

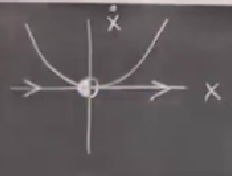
Soldan gelişte sabit noktaya "doğru" gittiğimiz için bunu bir stabil nokta yapmak istiyoruz, notasyonumuza göre içini dolduruyoruz. Ama sağa doğru giderken gayrı stabillik te var, eğer o noktada sağa doğru ufak bir sarsım uygulasak (perturb), sistem hemen sağa doğru büyüyecek. O zaman bu yarı-stabil bir sabit nokta. Bir tarafından sabit, diğer tarafından değil.

$\dot{x} = -x^2$ için durum tam tersi,

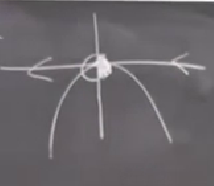
Sağdan stabil soldan değil. $\dot{x} = x^3$'e bakarsak,

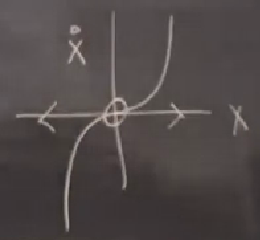
Bu tamamen gayrı stabil. Ve son olarak eğer $\dot{x} = -x^3$'e için,

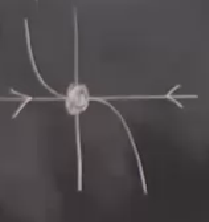
Tamamen stabil. Fakat buradaki stabillik daha önce gördüğümüzden biraz farklı; daha önceki üstel idi, bu tür noktalara doğru üstel bir çürüme olur. Üstteki durumdaki çürüme çok daha yavaş olurdu.

Özetle eğer $f'(x^\ast)=0$ olduğu durumda ne olup bittiğini anlamak istiyorsak, hemen grafiği çizmek faydalı. Bir alternatif Taylor açılımında daha yüksek derecelere bakmak (yani attığımız bazı terileri tutmak) fakat bence bu hala yanlış bir yaklaşım. Resimlere bakmak çok daha bilgi verici.

Örnek: Lojistik Denklem

Daha önce işlediğimiz bir denklem bu, hatırlarsak,

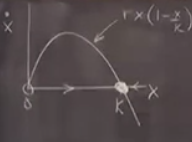
$$ \dot{x} = rx ( 1 - \frac{x}{K}) $$

ki $x$ nüfus sayısı, $K$ taşıma kapasitesi, $r > 0$.

$x^\ast=0$, ya da $x^\ast=k$ olduğu zamanda $\dot{x}=0$ olur. Sabit noktalar bunlar. Stabilite için $f'(x^\ast)$'e bakıyoruz,

$$ f'(x) = r - \frac{2rx}{K} $$

$f'(0) = r > 0$. Bu sonuç bize $x^\ast=0$'in gayrı stabil olduğunu söylüyor.

$f'(0) = r - \frac{2rK}{K} = -r < 0$, demektir ki $x^\ast=K$ stabil.

Dikkat: notasyon karışmasın, üstteki $r$ daha önce kullandığımız $r$'den farklı.

Neyse, böylece daha önce çizdiğimiz aynı resme ulaşıyoruz.

Burada lineerizasyon konusundan biraz uzaklaşıp, pür matematiğin basit diferansiyel denklemler (ODE) için olan mevcudiyet ve özgünlük (existence and uniqueness) kanununa değinmek istiyorum. Daha önce bir soru soruldu, bir sabit noktaya sonlu zamanda erişmek mümkün mü? Hatta erişmek bile mümkün mü? Bu sorunun cevabı bu kanun ile verilebilir.

Eğer $f(x)$ ve $f'(x)$ sürekli ise, $\dot{x} = f(x)$'in çözümü vardır ve bu çözüm özgündür. Tabii süreklilik özelliği mevcut ise aynı anda $f(x)$'in arka arkaya türevi alınabilir de demiş oluyoruz. Bu varsayımlardan yola çıkarak ODE'nin çözümü vardır diyoruz. Tabii bu tüm zamanlar için var anlamına gelmiyor, kısa bir süre için mevcudiyet olabilir, bir başlangıç noktasından ODE'yi başlattık diyelim, tüm $t$'ler için çözümün varlığı garanti olmayabilir. Çözüm $t=0$ etrafındaki bir bölgede vardır, bunu söyleyebiliriz.

Salınımın İmkansızlığı

$t \to \infty$ iken $\dot{x} = f(x)$ sistemi için $x(t)$ nasıl hareket eder? Ya $x(t)$ sonsuzluğa gider, ya da bir sabit noktaya yaklaşır. Bu kadar. İmkansız olan salınım (oscillation), periyodik bir çözüm, hatta sönümlü (damped) salınım bile mümkün değil.

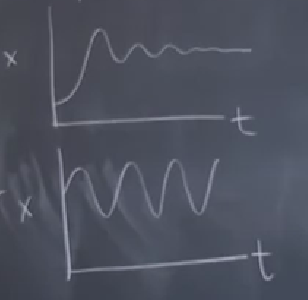
Bazılarının aklına şu soru gelebilir; "ama emin miyim, belki çok akıllıca bir $f$ uydurursam salınım olabilir?". Cevap, salınımın olmamasının topolojik sebepleri var. Sebep tüm $x(t)$ gidiş yollarının tekdüze (monotonik) şekilde artıyor ya da azalıyor olması, ya da yerinde kalması. Bu derste teorik ispatlarla çok uğraşmayacağız demiştim, ama mantıki, sezgisel olarak şunu söylemek mümkün olabilir; Alttaki resme bakalım,

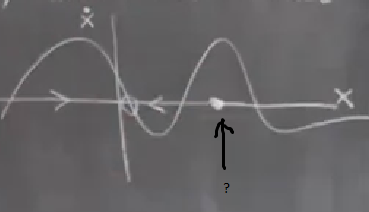
Salınım için ne gerekli? Diyelim ki okla gösterilen noktaya "doğru" gidiş var, sonra oradan "geriye" dönüş var. Fakat bu o noktadaki vektör alanının iyi tanımlanmamış (not well-defined) olduğu anlamına gelir. İyi tanımlı olmayan bir şeyi de matematiksel olarak kullanamayız. Çünkü o noktada farklı değerlerin olması $f(x)$'in "kafasına göre" aynı $x$ için bir öyle bir böyle değerler döndürdüğü anlamına gelir, bu da fonksiyon tanımına göre mümkün değildir. Yani aynı noktadan geçerken iki farklı yöne gidemeyiz.

"Ama bir dakika" diyebilir bazılarımız, "tek eksen üzerinde bir ileri bir geri giden harmonik salınım var". Evet ama bu sistem tek boyutlu değil, $\dot{x}$ ile değil $\ddot{x}$ ile tanımlı, ve bu türden sistemleri mesela bizim geometrik yaklaşımla çözmek için iki boyut gerekir, bir eksen $\dot{x}$ için bir eksen de $\ddot{x}$ için. Bu sistemleri dersin ilerisinde göreceğiz, onlar ikinci derece sistemler.

Çatallaşma (Bifurcation)

Diyelim ki bir boru üzerine bir kaya parçası koydum. Altta soldaki mesela ufakça bir kaya,

Bu kaya düşmeden yerinde durabilir, çünkü boru ona yeter. Fakat resimde sağda koca bir koya koyarsam, herhalde çöker. Ya sağa doğru küt diye, ya da sola, ama bir şekilde her şey aşağı iner. Bu örnek çatallaşma taşıyan sistemler için güzel bir örnek, sistemin bir parametresi var, dışarıdan uygulanan stress / kayanın büyüklüğü / ağırlığı mesela, ve bu parametrenin değişimi sonucu dramatik bir sonuç ortaya çıkıyor. Daha teknik dille şöyle diyelim: bir parametre değişirken sistemin vektör alanı çok büyük niteliksel değişimler yaşayabilir. Büyük değişim derken bir sabit noktanın yer değiştirmesinden bahsetmiyorum, yeni bir sabit nokta hiç yoktan ortaya çıkabilir, ya da tamamen yokolabilir mesela, ya da mevcut noktaların stabilitesi bile değişebilir. Bu tür değişimlere çatallaşma diyoruz. Çatallaşma değeri ise değişimin olduğu noktadaki parametre değeridir.

Eyer Düğümü Çatallaşması (Saddle Node Bifurcation)

Bu mekanizma yeni sabit noktaların ortaya çıkması veya yokolmasındaki en temel mekanizmadır. Standart örnek,

$$ \dot{x} = r + x^2 $$

ki $r$ kontrol parametresi, eğer bir fizik deneycisi isem bu $r$ dışarıdan sistemi kontrol ettiğim bir ayar düğmesi (knob), vs. Çizmek gerekirse, eşitliğin sağ tarafında bir parabol var, ama bir kesi değeri de var, ki bu kesi $r$. Kesi negatif olduğunda resim şöyle,

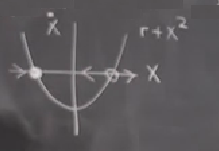
Elimizde iki tane sabit nokta var. Şimdi diyelim ki düğmeyi çeviriyoruz, ve $r$ yavaş yavaş sıfıra doğru çıkartıyoruz. Mesela sıfıra çok yaklaştık diyelim, bu noktada

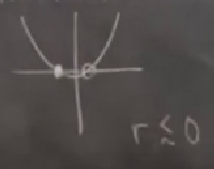
grafiği olurdu, parabol hala benzer şekilde, üste doğru açık, hala x ekseni çok az altından geçiyor. Eğer düğmeyi çevirirken üstteki grafiklerin değişimini izleyebilseydik, parabolun yavaş yavaş yukarı çıktığını ve iki sabit noktanın yavaş yavaş birbirine yaklaştığını görürdük. İnsanın aklına şu soru geliyor, sabit noktalar acaba birbirine "çarpar mı?". Çarparsa ne olur?. $r=0$ noktasında bu oluyor, ve sonucu aslında daha önce gördük, bir tarafı stabil diğer tarafı gayrı stabil olan bir sabit nokta.

Bu acaipliğin de nereden geldiğini böylece görmüş olduk, demek ki sistemi tam çatallaşma anında yakalamışız. Stabil ve gayrı stabil noktalar birleşmiş, bu sebeple bu karma durum ortaya çıkmış. Ve nihayet, $r>0$ durumunda,

Bu resimde hiç stabil nokta yok. İlk başta iki tane vardı, bu noktalar çarpıştı, ve sanki birbirlerini yok ettiler, geriye hiç bir sabit nokta kalmadı. Tüm bunları sadece tek bir parametreyi değiştirerek gözlemledik, ve niteliksel bir değişimi gördük.

Soru

Yarı-stabil sabit noktaların tek ortaya çıkma sebebi çatallaşma mıdır? [iyi soru çünkü bir sistemin büyük bir değişim yaşayacağını tahmin edebilmek için belki yarı-stabil noktalara odaklanmak iyi bir fikir].

Cevap

[Hoca şöyle bir düşündü ve] bunu söylemek yanlış olmaz, evet.

Çatallaşma Diyagramı

Çatallaşmaları birkaç figürü arka arkaya çizerek gösterebiliriz, ama tüm bu değişimi tek bir figürde göstermeye yarayan diyagramlar var, bunlara çatallaşma diyagramı diyoruz. $x^\ast$ ile $r$ iki eksende olacak şekilde ortaya çıkan eğrileri çizeriz. Bizim kontrolümüzdeki $r$'dir, onu değiştirirken $x^\ast$'e ne olduğunu gözlemleriz (ve grafikleriz).

$$ \dot{x}=0 \Rightarrow r + (x^\ast)^2 = 0 $$

$$ x^\ast = \pm \sqrt{-r} $$

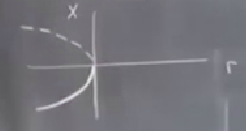
Koyu çizgi stabil noktaları temsil etmek için çizildi, kesikli olan gayrı stabil için. Niye negatif bölgede olanlar stabil? Daha önceki resimleri hatırlarsak, çarpışma öncesi mesela, solda (negatifte) olan sabit nokta stabil idi.

Eğer (saddle) sözünün nereden geldiğini niyahet görmüş olduk, şekil sola yatarılmış bir eğere benziyor. Kimisi bu tür çatallaşmalara "katlanmış" diyor, çünkü şekilde sanki bir düz çizgiyi alıp katlamışız sanki, başkaları dönme noktası diyor, çünkü bir daldan gelirken ötekine "dönüyoruz", vs. Ben eğer sözünü kullanacağım.

Bu çok temiz bir örnekti aslında, çatallaşmaları net bir şekilde görebildik. Sizin ileride karşınıza çıkabilecek problemlerde analiz bu kadar temiz olmayabilir. O türden bir örneği de görelim.

Örnek

$$ \dot{x} = r + x - \ln(1+x) $$

Bu oldukça okkalı, içinde gayrı lineer bir terim var, $\ln$. Bu sistemi $r$'nin bir fonksiyonu olarak incelemek istiyoruz. Önce sabit noktaları bulmak istiyoruz, $\dot{x}$'i sıfıra eşitliyoruz,

$$ r + x^\ast = \ln(1+x^\ast) $$

Ama şimdi başımız dönmeye başladı, eyvah, bunu $r$'nin fonksiyonu olarak nasıl tekrar düzenleyeceğiz? Aslında problemi dersten önce öyle seçtim ki bunu yapmak imkansız. Eğer eski analitik türden düşüncede takılıp kalmış olsaydım, şimdi felç olmuştum, tek adım atamazdım. Fakat biz bu derste grafiksel düşünmeyi öğrendiğimiz için çözümün aslında basit olduğunu görebiliriz, çünkü üstteki ifadenin grafiğini çizebilirim.

İki grafik çizerim, biri $y = r + x$ için diğeri $y = \ln(1 + x)$ için. Bu arada ilk dersin başında taslaksal olarak bir fonksiyonu hızlı bir şekilde grafikleyebilme becerisine sahip olmak iyi olur demiştim, işte bu beceri burada devreye giriyor, bu iki fonksiyonu pat diye çizebilmek lazım. Bilgisayarda çizebilirsiniz onları tabii, fakat bu daha yavaş olurdu. Önce $\ln(1+x)$,

Y eksenine $y$ dedim dikkat $\dot{x}$ değil. Aynı grafiğe şimdi $y = r + x$ çiziyorum,

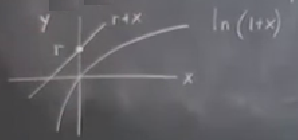
Kesi $r$, eğim 1. Şu anda bu iki eğri birbirini kesmiyor, bu ne demek? Kesişmiyorlarsa bu iki formül hiçbir $x$ için birbirine eşit değildir demektir, o zaman $r$ resimde görüldüğü gibi ise hiçbir sabit nokta yoktur demek.

Diğer yanda $r$'yi aşağı indirdikçe üstteki düz çizgi aşağı inmeye başlar, eğimi hala 1'dir tabii, ama bir noktada düz çizgi eğriyle kesişecek. Alttaki resimde bu kaydırmayı iki kez yapıyoruz, ilk kaydırma sonrası tek noktada kesişme olacak, sonraki kaydırma ardından iki noktada.

Bu sonuç daha önce işlediğimiz senaryoya benzemiyor mu? İlk başta hiç kök yok, sonra bir tane var, sonra iki tane. Eğer çatallaşmasının temeli bu zaten. Geometrik dilde teğetsel kesişme var ise eğer çatallaşması var diyebiliriz. Bu ne demektir? O kesişme noktasında hem düz çizginin hem de eğrinin eğimi aynıdır demektir, yani hem

$$ r + x = \ln(1+x) \qquad (1) $$

eşitliği doğru, hem de

$$ \frac{d}{dx} (r + x) = \frac{d}{dx} \bigg( \ln (1+x) \bigg) \qquad (2) $$

eşitliği doğru olmalı. Türev aldık çünkü türev bize belli bir noktada eğimi verecek, ki sonra o iki eğimi karşılaştırabilelim. Bu denklemler sayesinde bize gerekli $r,x$ kombinasyonlarını bulabiliriz. (1) formülünü çözemeyeceğimizi biliyoruz, fakat (2)'yi çözmek kolay.

$$ 1 = \frac{1}{1+x} \Rightarrow x^\ast = 0 $$

eğer çatallaşması anında.. Bu sonucu (1)'e sokarsak,

$$ r - \ln(1) = 0$$

elde ederiz. Üstteki $r$ sonucuna kritik andaki $r$ diyelim, notasyon olarak $r_c$. İlginç bir durum, üstteki resmim fena değilmiş demek ki, çünkü o resim de yaklaşık $r=0$ sonucunu gösteriyor. Sonuç, çatallaşma $(x,r)=(0,0)$ noktasında ortaya çıkıyor.

Şimdi (0,0) etrafındaki vektör alanını açarsak ne olur? $\dot{x}$ üzerinde ufak bir Taylor açılımı yaparak bunu görebiliriz belki. Önce hatırlayalım, $\ln(1+x)$'in McLaurin açılımı

$$ \ln (1+x) = x - \frac{x^2}{2} + \frac{x^3}{3} + ... , \quad |x|<1 \textrm{ için}$$

Şimdi

$$ \dot{x} = r + x - \ln(1+x)$$

$$ \approx r + x - \big[ x - \frac{x^2}{2} + \frac{x^3}{3} + ... \big] $$

$x$'ler iptal olur,

$$ = r + \frac{x^2}{2} + O(x^3) $$

3 ve üstü derecedeki terimler diğerlerine nazaran çok daha küçüktür, onları atabiliriz. Elde ettiğimiz formüle bakarsak, çatallaşma yakınında elde ettiğimiz vektör alanı tanıdık aslında. Bölü 2 kısmını dikkate almayalım şimdi, geri kalan $r + x^2$ formülü eğer noktasında elde ettiğimiz şey idi. Çatallaşmaya yakın yine bu formülü elde ettik. Bazıları bu $r + x^2$'e bir tür şablon diyor, onu " normal form" olarak adlandırıyorlar. Eyer düğümleri etrafında neler olduğunu inceleyen ciddi araştırmalar, ciddi teoriler var, şimdi burada onlara girmek istemiyorum ama o bölgedeki dinamik her zaman $r$ artı bir sabit çarpı $x^2$ formunda oluyor.

Transkritik Çatallaşma

Bu tür çatallaşmaların normal formu

$$ \dot{x} = rx - x^2 $$

Bu form daha öncekine kıyasla niceliksel bir fark yaratıyor, eşitliğin sağ tarafını açarsak,

$$ = x(r-x) $$

İki sabit nokta hemen ortaya çıkar, $x^\ast=0$ her $r$ için sabit noktadır. Öteki ise $x^\ast = r$. Önceki örnekte sabit noktalar ortaya çıkıyor, yokoluyordu, burada yokedilemez bir sabit nokta var, $x^\ast=0$, $r$'yi değiştirerek bu arkadaşı ortadan kaldıramıyoruz.

Doğal bilimlerden örnek düşünmek gerekirse, mesela biyolojik nüfus konusunu inceliyorsak, belli bir tür organizma bir ekolojide hiç yok ise, o organizmadan o ekolojide gelecekte de hiç olmayacaktır; sıfır bir sabit noktadır. Neyse, sabit noktayı yokedemiyoruz ama, onun stabilitesini değiştirmek mümkün. Transkritik formunda olan tam da bu.

Lineerizasyona bakalım,

$$ f'(x) = \frac{d}{dx} (rx - x^2) = r - 2x, \quad f'(0) = r$$

Bu demektir ki $x^\ast = 0$ noktası eğer $r<0$ ise stabil, $r>0$ ise gayrı stabildir. Diğer nokta $r$'yi kontrol edelim,

$$ f'(r) = r - 2r = -r $$

İlginç bir sonuç çıktı, bu noktanın $f'$ fonksiyonu diğerinin tam tersi, yani bir nokta stabil ise diğeri değil, biri gayrı stabil ise diğeri stabil.

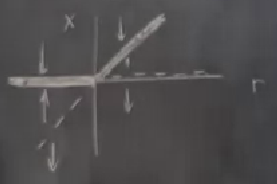
Bazı araştırmacılar bu duruma "stabilitenin değiş tokuşu" ismini de vermişler, biz transkritik diyoruz tabii, ama bu isimlendirme de fena değil, grafiğe bakarsak soldan x eksen üzerinde stabil geliniyor, sonra öteki sol alttan gelen gayrı stabilite ile "çarpışma" var, bunun ardından stabilite değiş tokuş ediliyor.

Peki $r=0$ noktasında neler oluyor? Bu noktada $\dot{x}=-x^2$, iki sabit noktanın çarpışması var, fakat birbirlerini yoketmiyorlar. Birbirleri "içinden geçiyorlar" sanki, ve o sırada birbirlerini değiştiriyorlar.

Tırmık Çatallaşması

Simetrili sistemlerde ortaya çıkar. Mesela,

$$ \dot{x} = rx - x^3 $$

Burada $x$ ve $-x$ arasında simetri var. Vektör alanı $\dot{x},x$'e bakalım, yavaş yavaş ortaya çıkartalım grafiği, eğer $r<0$ ise ve orijinde isem negatif bir eğim var [önce orijinde sola yatık ufak bir çizgi parçası çiziyor, sonra oradan geçen daha büyük grafiği çiziyor],

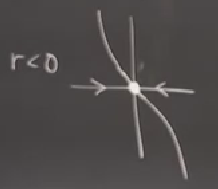
Orijinde tanıdık bildik türden bir sabit stabil nokta var. $r=0$ noktasında da bir sabit nokta var, fakat, daha önce değindiğimiz gibi, "agresif" bir şekilde, yani üstel türden bir stabil nokta değil, ama yine de stabil tabii.

$r>0$ olduğu zaman alttaki ortaya çıkar,

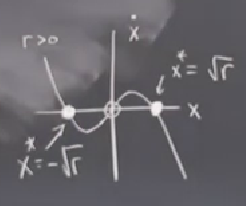
Burada ilginç olan simetrik iki sabit noktanın olması. Faktorize edince de görebiliriz bunu, $\dot{x}=x(r-x^2)$, ve bunu sıfıra eşitleyince üstteki noktalar ortaya çıkar. Eğer türünde sıfır düğüm bir düğüm sonra iki düğüm oluyordu, transkritikte iki düğüm bire, oradan iki düğüme gidiyor, tırmık türünde ise bir düğüm bir düğüm, sonra üç düğüm oluyor. İlginç. Terminolojide üstteki örnek süperkritik tırmık (supercritical pitchfork) olarak biliniyor. Süperkritik kelimesini dinamik sistemlerde çok duyarsınız, anlamı şudur, çatallaşan çözümler stabildir. Üstte de görülüyor, iki uçtaki çatallaşan sabit noktaların ikisi de stabil.

Tırmık kelimesinin sebebi ise şu diyagramda görülüyor,

Şekil sağa dönük bir tırmığa benziyor.