Ders 15

Önceki derslerde gradyan kavramını gördük. Bu vektörün bileşenleri, 3 değişkenli bir fonksiyon için

$$ \nabla f = < f_x, f_y, f_z > $$

idi, ki bu bileşenler $f$'in tüm kısmı türevlerini oluşturuyordu. Gradyanlar kısmı türevleri paketlemenin, sunmanın yöntemlerinden biriydi sadece.

Gradyanları yaklaşıksallama formülleri için de kullanabiliyorduk, mesela eğer $x,y,z$'yi "birazcık" değiştirince bunun $f$ üzerindeki değişim etkisi $\Delta f$'i [kabaca, niye kabaca olduğu altta] hesaplamak istiyorsak bunun gradyan formundaki hali

$$ \Delta f \approx f_x \Delta x + f_y \Delta y + f_z \Delta z $$

Daha kısa olarak

$$ = \nabla f \cdot \Delta \vec{r} $$

oluyordu, yani gradyan vektörünün, pozisyon vektörünün değişimi ile olan noktasal çarpımı. Kısmı türevlerin tamı tamına ölçtüğü şey $f$'in bir değişkendeki değişime ne kadar hassas olduğudur, ve bu hassaslığın ufak değişimler ile çarpılıp toplanması bize tüm fonksiyondaki değişimi verir.

Üstteki yaklaşıksallama "teğet düzlem yaklaşıksallaması" olarak bilinir, bu arada, fonksiyonun yerine bir noktada teğet düzlemi koyuyoruz, o noktada fonksiyon budur diyoruz, böylece fonksiyonun $x,y,z$ değişkenlerine aşağı yukarı lineer olarak bağlı olduğunu farz ediyoruz, o sebeple zaten değişimleri düz çarpım sonrası basit toplama maruz tutuyoruz.

Hatırlarsak, $f(x,y,z)=c$ yüzeyine teğet olan düzlemi bulmak için normal vektöre bakarız, biliyoruz ki normal vektörlerden biri fonksiyonun gradyan vektörüdür, çünkü gradyanın kesit seviyelerine diktir, ve fonksiyonun daha yüksek değerlerine, en yüksek artış yönüne işaret etmektedir.

Bu noktada kültürel bir not eklemek istiyorum. Bunu belki haftalar önce belirtmeliydim, daha iyi olurdu. Kısmı türevleri niye seviyoruz / kullanıyoruz? Önemli bir sebep onların fizik için çok faydalı olmaları, etrafımızdaki dünyayı anlamamıza yardımcı olmaları. Bu dünyadaki pek çok oluş kısmı türevsel denklemler (partial differential equations -PDE-) ile tarif edilir, modellenir.

PDE'ler bilinmeyen bir fonksiyonun kısmı türevlerini kullanarak onlar arasında bir ilişki, fonksiyon kurar.

Mesela Isı Denklemi (Heat Equation) bunlardan biridir.

$$ \frac{\partial f}{\partial t} = k ( \frac{\partial^2 f}{\partial x^2} + \frac{\partial^2 f}{\partial y^2} + \frac{\partial^2 f}{\partial z^2} ) $$

Bu denklemde çözmek, bulmak istediğimiz $f$ fonksiyonudur, ve bu fonksiyon 4 değişkene bağlıdır: $f(x,y,z,t)$, ve temsil ettiği $x,y,z$ pozisyonundaki bir noktanın $t$ anındaki sıcaklığıdır. PDE $\partial f/\partial t$ ise bu fonksiyonun zamana göre nasıl değiştiğini tarif eder.

Bu konuya ileride tekrar döneceğiz.

Şimdi diğer konulara geçelim. Kritik noktalardan bahsetmiştik, bu noktalarda kısmı türevler sıfır değerlerindeydi. Ayrıca eğer noktaları (saddle points) vardı, ve ikinci türevleri kullanarak kritik noktanın min mi, maks mi, eğer mi olduğuna karar verebiliyorduk.

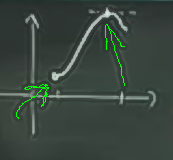
Fakat tüm bunların min, maks bulmak için yeterli olmadığını da gördük, çünkü min, maks sınır noktalarında, fonksiyonun ta en uçlarında da olabiliyordu.

Üstteki grafikte görülen sağdaki nokta kritik bir nokta, ve ikinci türevin bize lokal maks olduğunu söyleyeceği noktadır. Mınimum ise soldaki noktadır, fonksiyonun sol sınırındadır, ve kritik nokta değildir. Birden fazla değişken için de durum aynıdır; bu durumlarda min, maks bulmak için değişkenlerin olabilecekleri en az değere (mesela sıfır) ya da en fazla (mesela sonsuzluk) çekmek gerekebilir. Yani zihnimizi açık tutup pek çok olasılığı gözden geçirmemiz, düşünmemiz gerekir.

Diferansiyeller

$f$'teki değişimi şöyle gösterdik

$$ df = f_xdx + f_ydy + f_zdz $$

İlk bakışta bu temsil, kısmı türevleri paketlemenin bir başka yolundan ibaret gözüküyor. Bunu da yapıyor muhakkak, ama daha fazlası da var. Yaklaşıksal formüllerin formunu hatırlamanın iyi bir yolu, her değişkendeki varyasyonu diğerlerinkiyle ilintilendiriyoruz. Bir önemli fayda daha su, bu formülü aynı $d_$ ile bölerek, değişik şekillerdeki Zincirleme Kanunlarını ortaya çıkarabiliriz.

Mesela diyelim ki $x,y,z$ diğer iki değişken $u,v$'ye bağlı.

$$ x = x(u,v) $$

$$ y = y(u,v) $$

$$ z = z(u,v) $$

Bu durumda $f$, aslında $u,v$'nin bir fonksiyonu haline gelir. Ve bu noktada kendimize $f$ fonksiyonu mesela "$u$'nun değişimine ne kadar hassas" gibi bir soru sorabiliriz. Bunun cevabını Zincirleme Kanununu $u$ üzerinden kullanarak verebiliriz.

$$ \frac{\partial f}{\partial u} = \frac{\partial f}{\partial x}\frac{\partial x}{\partial u} + \frac{\partial f}{\partial y}\frac{\partial y}{\partial u} + \frac{\partial f}{\partial z}\frac{\partial z}{\partial u} $$

Üstteki türde bir işlem bize değişken değişimi yaptığımız zaman faydalı olur. Mesela kutupsal kordinat sisteminden $x,y$ kordinat sistemine geçiş yapabiliriz, ve Zincirleme Kanunu üzerinden kutupsal formdaki değişimin $x,y$ dünyasındaki yansımalarını hesaplayabiliriz.

Sonraki konumuz bağımsız olmayan değişkenler, mesela $x,y,z$, değişkenleri $g(x,y,z)=c$ gibi bir fonksiyon üzerinden birbiriyle bağlantılı. Her seferinde bu tür problemlerde istediğimiz değişkeni yanlız bırakıp, başka bir yerlere koyamıyoruz, o zaman min, maks bağlamında Lagrange Çarpanları tekniğini kullanıyoruz.

Bir diğer gördüğümüz teknik kısıtlanmış kısmı türevler tekniğiydi. Diyelim ki yine elimizde $f(x,y,z)$ var ve $g(x,y,z)=c$ gibi bir bağlantı var. Bu durumda $f$'in tek bir değişken değişip, diğerleri sabit iken (yani tipik kısmı türev işlemi) nasıl değişeceğini bulabilir miyim?

Bulamayabilirim, çünkü, belki kısıtlama ibaresi $g$ yüzünden geri kalan tüm değişkenleri sabit tutamayacağım.

Örnek

Şunu bul

$$ \bigg( \frac{\partial f}{\partial z} \bigg)_{y} $$

$y$ sabit

$z$ değişiyor

$$ x = x(y,z) $$

Üstteki $x$ ibaresini bu örnek için biz tanımladık, herhangi başka bir kısıtlama ibaresi $g$ olabilirdi.

1) Diferansiyelleri Kullanarak

Genel ifade neydi?

$$ df = f_xdx + f_ydy + f_zdz $$

Bunu özel durumumuza nasıl uygularız? $y$ sabit, o zaman $dy = 0$. Yani

$$ df = f_xdx + f_zdz
\qquad (1) $$

Devam edelim, aslında $dx$'den de kurtulmak istiyoruz, çünkü o bağımlı bir değişken, her şeyi $z$ formunda görmek istiyoruz. Bunun için önce $dg$'yi bulalım.

$$ dg = g_xdx + g_ydy + g_zdz = 0 $$

Niye sıfıra eşit? Çünkü $g$ kısıtlama ibaresi sabitti.

$y$ değişmiyorsa, o zaman üstteki $dy$ de gidebilir. Kalanlar

$$ dg = g_xdx + g_zdz = 0 $$

$$ dx = -\frac{g_z}{g_x}dz $$

Yani

$$ \bigg( \frac{\partial x}{\partial z}\bigg)_{y} = -\frac{g_z}{g_x} $$

O zaman iki üstteki formülü alıp, (1). formülde $dx$ yerine koyarsak

$$ df = (-f_x\frac{g_z}{g_x} + f_z) dz $$

Örnek Test 2A Problem 2

Kesit seviyeleri veriliyor, bunlar üzerinde b) için $h$ = 2000, $\partial h/\partial x = 0$ ve $\partial h/\partial y < 0$ olduğu noktayı işaretle denmiş. Hoca noktalar ile $h=2200$ seviyesini işaretliyor.

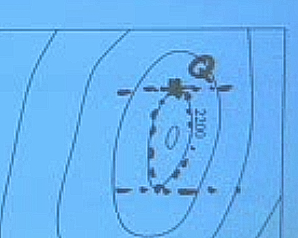
Sonra yatay çizgilerle $\partial h/\partial x$'i işaretlemiş, bu çizgiler boyunca $y$ sabit, ve $x$ değişiyor. Değişirken, kesit seviyeleri arasından geçiyoruz, önce azalıyoruz, sonra çoğalıyoruz, aradaki noktada (iki noktada, bir üstte, bir altta) $h=2200$'e teğet geçiyoruz.

Soru bir de $\partial h/\partial y < 0$ olan noktayı istemiş, bu son şart, elimizde iki noktadan yukarıda olanı, orası $Q$ olacak.

İstenen bir diğer şey $\partial h/\partial y$ değerinin $Q$ noktasında yaklaşıksal olarak değeri. Bunun için $Q$'den bir sonraki kesit seviyesindeki bir noktaya $Q'$ zıplarız. Ve bu iki nokta arasındaki ölçümlere göre bir yaklaşıksal hesap yaparız.

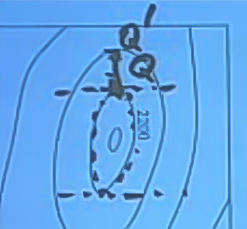
$$ \Delta y \approx 1000 / 3 = 300 $$

1000, 3 nereden geldi? Problemin altında bir skala verilmiş, bu skala 1000 birimlik büyüklüğün ne olduğunu göstermiş. Çıplak gözle bakınca, iki nokta arasındaki $y$ farkının kabaca bu skaladaki 1000 değerinin üçte birini olduğunu görüyoruz. 3 ile bölmek oradan geliyor.

$$ \Delta h = -100 $$

Bu yaklaşık değil, dikkat, tamı tamına -100. Çünkü kesit seviyeleri arasındaki $h$ değerlerini problem kesin olarak veriyor.

$$ \frac{\Delta h}{\Delta y} = -\frac{100}{300} $$

$$ = -\frac{1}{3} $$

Yani

$$ \frac{\partial h}{\partial y} \approx -\frac{1}{3} $$