Ders 5

Bir çizginin formülünü iki düzlemin kesişimi olarak gördük, fakat bu şekilde bir tanım çoğunlukla bir çizgiyi tanımlamak için en rahat / uygun yol değildir, çünkü elinizde bazı denklemler var, bunları çözmekle uğraşmak lazım, vs.

Şöyle bir yöntem daha iyi olmaz mıydı? Herhangi çizgi üzerinde bir nokta hayal edelim, ve bu noktanın herhangi bir t(zaman) değeri için bu çizgi üzerinde farklı bir konuma sahip olduğunu düşünelim. Herhangi bir t değeri için, çizgi üzerindeki konumu bulabiliriz. Bu şekilde çizgi üzerindeki tüm noktaların konumlarını tanımlayabiliriz. Bu tür parametreye bağlı denklemlere -ki bu örneğimizde parametre t'dir- parametrik denklemler denir.

Örnek:

Çizgi üzerinde iki nokta belirleyelim.

$$ Q_0 = (-1,2,2) $$

$$ Q_1 = (1,3,-1) $$

Güzel, bu iki nokta var ama ötekilerini nasıl tanımlarız? Bu iki noktasının arasında, sonrasında, öncesinde olan tüm noktalar da çizgiye dahildir.

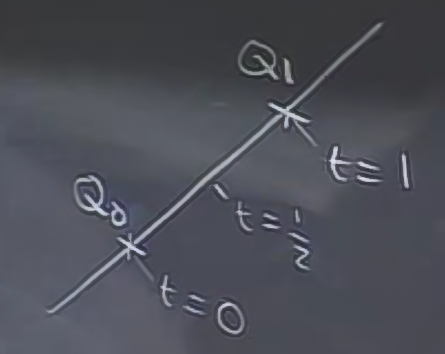
Zaman aralıklarını öyle düşünelim ki, zaman indeksi sıfır ($t=0$) noktasında iken, çizgi $Q_0$ üzerinde, tek birim adım atıldığında ($t=1$) ise $Q_1$ üzerinde olsun. O zaman yarım birim zamanda denklemimiz iki noktanın tam ortasını işaret eder.

Böylece çizgiyi temsil etmenin yolu onu $t$ bazında hareket eden noktanın geçtiği yerler olarak tanımlamaktır. Bu temsilin en basit hali eğer hareket sabit hızda olursa olur.

$t$ anındaki pozisyon $Q(t)$ nedir?

Sorunun cevabını şöyle vermeye başlayabiliriz: $\vec{Q_0Q(t)}$ vektörü $\vec{Q_0Q_1}$ birbiriyle orantılıdır. Bu orantı neye eşittir?

Bu oran $t$'ye eşittir. O zaman,

$$ \vec{Q_0Q(t)} = t \ \vec{Q_0Q_1} $$

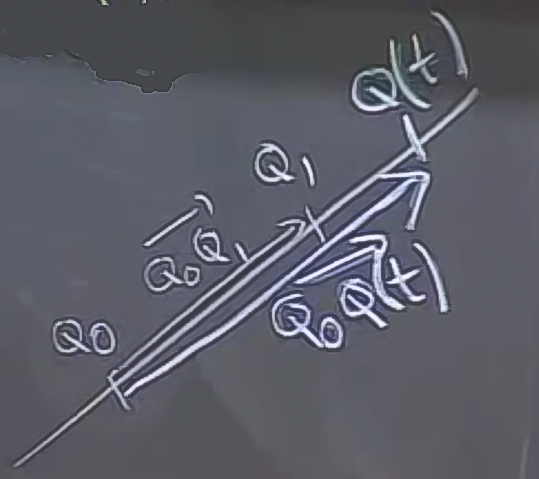
O zaman iddia ediyorum ki bu formülü kullanarak örneğimizdeki hareket eden noktanın yer formülünü bulabilirim.

$$ \vec{Q_0Q(t)} = t \ <2,1,-3> $$

Şimdi çizgi üzerinde hareket eden noktanın formülü $Q(t)$'yi şu şekilde temsil edelim

$$ Q(t) = $$

O zaman

$$ x(t) + 1 = 2t $$

$$ y(t) - 2 = t $$

$$ z(t) - 2 = -3t $$

Üsttekiler, alttaki şu formun açılımından ibaret aslında

$$ Q(t) = Q_0 + t \ \vec{Q_0Q_1} $$

Üstteki üç formül bu derste gördüğümüz ilk parametrik çizgi formülü. Aslında formüle baktığımız zaman t sıfır değeri için denklemin $Q_0$ noktasını işaret ettiğini görebiliyoruz. Bu değer, bizim başlangıç noktamızdır, ve t'nin pozitif veya negatif oluşuna göre pozitif veya negatif yönde ilerleyebiliriz. Formülün parçaları olan $x(t),y(t),z(t)$ sadece $t$'nin fonksiyonudurlar, ve hep $t$ ile bir katsayının çarpımı, artı bir sabit formundadırlar. $t$'nin katsayıları çizgi üzerindeki vektör hakkında bilgi verir, ve sabitler ise $t=0$ anında nerede olduğumuzu gösteren başlangıç değerleridirler.

Uygulama - Bir Düzlem ile Kesişme

Düzlem $x+2y+4z=7$. Çizgi biraz önceki formül olsun. Kesişme var mıdır, var ise nerededir?

Önce şu soruyu soralım kendimize. $x+2y+4z=7$ düzlemine göre, $Q_0 =(-1,2,2)$ ve $Q_1 = (1,3,-1)$ noktaları düzlemin

• Aynı tarafında
• Farklı taraflarında
• Bir tanesi düzlem üzerinde
• Karar veremiyorum

Cevaplayın.

$Q_0$ ve $Q_1$ noktalarını düzlem formülünün sol tarafına sokarız. $Q_0$ için sonuç $>7$, düzlem üzerinde değil, $Q_1$ için sonuç $<7$, yine düzlem üzerinde değil. Peki noktalar düzlemin hangi tarafında? Farklı tarafında, çünkü biri $<7$, öteki $>7$ sonuç verdi. Bir düzlem uzayı iki yarı-parçaya ayırır ve noktalar bu ayrı parçalardadırlar. Doğru cevap "Farklı tarafında"dır.

Uygulamamızda cevaplanmayan bir soru daha var. Kesişme noktası neresidir? $Q(t)$ nedir? Şöyle

$$ x(t) + 2y(t) + 4z(t) $$

$$ = (-1+2t) + 2(2+t) + 4(2-3t) $$

Basitleştirelim

$$ = -8t + 11 $$

Bu formülü $7$ ile karşılaştıralım çünkü $Q(t)$ nin düzlem üzerinde olduğu an $-8t + 11 = 7$ olduğu andır. Cebirsel olarak $t$'yi elde edebiliriz, sonuç $t=1/2$. Bu değeri $Q(t)$'ye koyarsak

$$ Q(\frac{1}{2}) = (0,\frac{5}{2},\frac{1}{2}) $$

Kesişim noktası eşitliğin sağındaki değerdir.

Yani eğer çizginin parametrik denklemini biliyorsak, onu düzlem formülüne sokarız, ve kesişimin hangi noktada olduğunu hemen hesaplayabiliriz.

Şimdiye kadar gördüklerimizden parametrik denklemlerin çizgileri temsil etmek için iyi bir yöntem oldukları belli olmuştur herhalde. Bunun ötesinde parametrik denklemler uzaydaki herhangi bir eğriyi (curve), herhangi bir hareketi (trajectory), yolu temsil etme kabiliyetine de sahiptir.

Genel bağlamda söylemek gerekirse, parametrik denklemleri bir uzayın içindeki veya bir düzlem üzerindeki herhangi (arbitrary) bir hareketi temsil etmek için kullanabiliriz.

Cycloid (Yuvarlanma Eğrisi)

$a$ yarı çapındaki bir tekerlek yerde -x ekseninde- dönerek ilerliyor, $P$ bu tekerleğin dış yüzeyinde (rim) bir noktadır ve başlangıç noktası 0 üzerindedir. Bu durumda ne olur? Daha detaylı olarak sormak gerekirse, $P$ noktasının hareketini $t$'nin bir fonksiyonu $x(t),y(t)$ olarak ifade ebebilir miyiz?

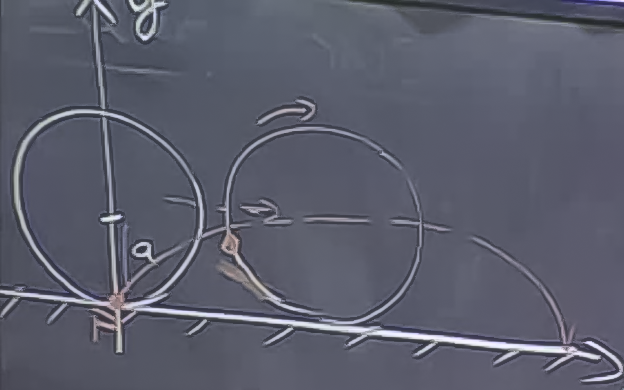
(x ekseni biraz sağa yatik çıkmış ama bu video kamerasının açısı yüzünden). Bu örneği bir bisikletin tekerliğine takılmış bir ışığın, bisiklet gece giderken ortaya çıkartabileceği görüntüyü düşünürek te hayal edebiliriz. Yani hem dönüş hareketi var, hem de yatay olarak düz bir gidiş hareketi var.

Bu $P$ noktasının gidiş yolunu hesaplamak için tekerleğin ne kadar hızlı döndüğü önemli mi? Hayır değil. Yavaş da döndürsek hızlı da döndürsek, $P$ aynı noktalardan geçecektir.

Bu problemde en önemli faktör zaman değil, mesafe, tekerleğin ne kadar mesafe katettiği. Ya da daha bile iyisi, mesafe ile dönüş birbirine bağlantılı olduğuna göre, ayrıca problemdeki en çetrefilli, girift oluşturan hareket dönme hareketi (rotation) olduğu için, belki de tekerleğin ne kadar döndüğünü gösteren bir açı değeri kullanırsak belki daha faydalı olacak. Pek çok değişik temsil yöntemi olabilir, fakat açıya göre parametrize edersek en temiz formülü elde etmek mümkün olur. O zaman $x(t),y(t)$ yerine $x(\theta),y(\theta)$ kullanalım.

Yani $x(\theta),y(\theta)$ ile tekerleğin ne kadar dönmüş olduğunu belirleyen $\theta$ açı üzerinden tanımlı bir fonksiyon kullanalım.

Tekerleğin nerede olduğu bilgisini ise $\vec{OP}$ vektörü ile temsil edebilirim. Buradaki tek problem vektör $\vec{OP}$ hakkında hiç bir şey bilmiyorum. Ama belki daha basit vektörler hakkında bir şeyler biliyorumdur. Mesela $\vec{AB}$ basit gibi duruyor, aynı şekilde $\vec{OA}$ fena değil, $\vec{BP}$ aynı şekilde. Peki $\vec{OP}$'yi bu daha basit vektörler üzerinden temsil edemez miyim? Edebilirim.

$$ \vec{OP} = \vec{OA} + \vec{AB} + \vec{BP} $$

O zaman bu basit vektörleri hesaplayabilirsem, daha zor olan $\vec{OP}$'yi de hesaplarım.

$$ \vec{OA} = < a\theta, 0 > $$

Niye? Vektörün $y$ bileşeni sıfır, bu bariz.

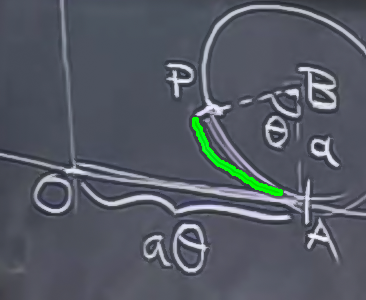
Peki niye $a\theta$? Eğer kayma, boşta dönme gibi şeyler yok ise, bu tekerleğin dış çemberinin katettiği mesafe (üstte yeşil ile işaretli), tekerleğin gittiği yer mesafesi ile aynıdır. Bu yüzeylerden birinin kavisli, diğerinin düz olması bu gerçeği değiştirmez. Yeşil ile işaretli dış çember parçasının $a\theta$ ile hesaplandığını basit matematikten biliyoruz (eğer $\theta$ radyan biriminde ise tabii, zaten bu sebeple -işleri basitleştirdiği için- matematikte hep radyan birimi kullanılır).

$\vec{AB}$ daha kolay, $x$ bileşeni sıfır, $y$ yönüne yarıçap kadar gitmiş.

$$ \vec{AB} = <0, a> $$

En son vektör $\vec{BP}$ biraz daha zor. Bu vektör hakkında neler biliyoruz? Büyüklüğünü yani $|\vec{BP}|$'yi biliyoruz ve dikey eksen ile $\theta$ kadar bir açı oluşturduğunu biliyoruz. Daha yakından bakarsak

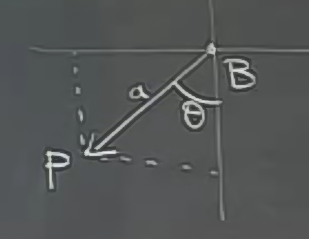
$$ \vec{BP} = <-a\sin(\theta), -a\cos(\theta)> $$

Şimdi ekleme aşamasına geldik.

$$ \vec{OP} = < a\theta - a\sin(\theta), a-a\cos(\theta) > $$

Ve nihayet cevabımızı bulduk. Çünkü

$$ \vec{OP} = < \underbrace{a\theta - a\sin(\theta)}_{x(\theta)}, \underbrace{a-a\cos(\theta)}_{y(\theta)} > $$

Bu problemi modellerken zihnimizde oluşan, istifade ettiğimiz şekil şu:

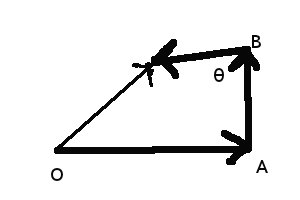
çünkü vektör toplamının geometrik olarak nasıl işlediğini biliyoruz ve eksik kalacak tek parça, basit toplamayla elde edebileceğimiz, aradığımız parametrik vektör olacak. Bu yöntemi seçmemizin bir diğer sebebi üstteki parçaların hepsinin basit hesaplanabiliyor olması, her üç vektör için de yarıçap $a$ mutlaka bir hesaba dahil, ve bu yarıçap hiç değişmeyen bir şey, dolayısıyla modellememizi basitleştiriyor. Yine benzer bir sebeple $\theta$ $\vec{OP}$ vektörünün x-ekseniyle oluşturduğu açı değil, $\vec{BP}$'nin y-ekseniyle oluşturduğu açı. Böylece onun üzerinden ve $a$ ile üç vektörü hızlı bir şekilde hesaplayabiliyoruz.

Ayrıca modellemede parametre $t$ değil, $\theta$. Bu mantıklı, çünkü değişimi ile tüm vektör öğelerini bir şekilde etkileyen (ayrı formüller üzerinden tabii) her dış değişken bir parametre olarak kullanılabilir.

Şimdi gizemli bir noktayı inceleyelim. Tekerleğin dönmesi sonucu takip edilen noktanın yere değip, tekrar yukarı çıktığı anda, oluşan takip çizgisi ne şekildedir? Bilgisayar grafiğine bakalım;

Sekil sunlardan hangisidir?

Bu cevabı vermenin en iyi yolu, formüllerimizi kullanmak.

Formülleri basitleştirmek için eğer $a=1$ alırsak,

$$ x(\theta) = \theta - \sin \theta $$

$$ y(\theta) = 1 - \cos \theta $$

Şimdi yaklaşım yaparak düşünmeye uğraşalım. Çok küçük $\theta$ için $\sin(\theta) \approx \theta$ ve $\cos(\theta) \approx 1$. Bunları $x(\theta), y(\theta)$ içinde kullanırsak, biri 0, öteki 1 çıkacak, bunlar pek net sonuçlar değiller. Demek ki bize daha iyi yaklaşım teknikleri (approximation) gerekiyor.

Tek Değişkenli Kalkülüs dersinde bize Taylor yaklaşımı (Taylor Approximation) öğretilir.

Taylor Yaklaşımı

Ekler

Taylor Serisi

Bir fonksiyon $f(x)$'in bir kuvvet serisi (power series) toplamı olduğunu farzedelim [3, sf. 805],

$$ f(x) = a_0 + a_1(x-a) + a_2(x-a)^2 + a_3(x-a)^3 + ... + a_n (x-a)^n + ...$$

Aslında $x-a$ yerine sadece $x$ kullanabilirdik, fakat $x-a$ kullanmanın cebirsel olarak bazı faydaları var; bunu birazdan göreceğiz.. Şimdi bu fonksiyonun ardı ardına türevini alalım,

$$ f'(x) = a_1 + 2a_2(x-a) + 3a_3(x-a)^2 + ... + n a_n(x-a)^{n-1} + ...$$

$$ f"(x) = 1 \cdot 2a_2 + 3 \cdot 2a_3(x-a) + .. $$

$$ f"'(x) = 1 \cdot 2 \cdot 3 (x-a) + .. $$

Taylor Serilerinin ana numarası ilk başta gördüğümüz serinin katsaylarının içini doldurmak için üstte gördüğümüz türevleri kullanmasıdır, böylece bir fonksiyonun istediğimiz kadar derecedeki türevlerini kullanarak o fonksiyonu belli bir noktada ($x=a$) yaklaşıksal olarak temsil edebiliriz. Katsayıları şöyle doldururuz, mesela ana formüldeki $a_0$ ne olacak? Ana formülde $f(a)=a_0$. Peki $a_1$? İlk türeve bakalım,

$$ f'(a) = a_1 $$

Bu basit ifade mümkün oldu çünkü $x=a$ deyince tüm $x-a$ içeren ifadeler sıfır haline geldi ve denklemden çıktılar. $a_2$ için

$$ \frac{f"(a)}{1 \cdot 2} = a_2 $$

Bu katsayıları ana formülde yerine koyalım (sadece $a_0,a_1,a_2$ için)

$$ f(x) = f(a) + f'(a)(x-a) + \frac{f"(a)}{2}(x-a)^2 + .. $$

İşte Taylor yaklaşımı budur! Ana formülü kaç polinom derecesi ile temsil etmek istediğimize göre üstteki türevlerin sayısı artabilir ya da azalabilir, bu probleme göre yapılması gereken bir seçidimdir - çoğunlukla iki derece yeterlidir.

Derse dönelim,

Küçük $t$ değerleri için

$$ f(t) \approx f(0) $$

Bu kabaca bir yaklaşımdır tabii ki. Biraz daha iyisi için, eğer $t$ kadar değişim olursa, bu değişimin şu şekilde eklenebileceğini farzederiz.

$$ f(t) \approx f(0) + tf'(0)$$

Biraz daha iyisi için

$$ f(t) \approx f(0) + tf'(0) + \frac{t^2}{2}f"(0)$$

Buna istediğimiz kadar devam edebiliriz

$$ f(t) \approx f(0) + tf'(0) + \frac{t^2}{2}f"(0) + \frac{t^3}{6}f"'(0)$$

Bu tekniği şimdi kullanalım

$$ \sin \theta \approx \theta - \frac{\theta^3}{6} $$

$$ \cos \theta \approx 1 - \frac{\theta^2}{2} $$

O zaman

$$ x(\theta) \approx \theta - (\theta - \frac{\theta^3}{6}) \approx \frac{\theta^3}{6} $$

$$ y(\theta) \approx 1 - (1 - \frac{\theta^2}{2}) \approx \frac{\theta^2}{2} $$

Bu değerlerden hangisi $\theta$ küçük iken daha büyük? $y(\theta)$. Yani $|x| << |y|$. Daha net bir sayı için bu iki büyüklüğün oranına bakabiliriz, bu bize bir eğim bilgisi verecektir.

$$ \frac{y}{x} = \frac{\theta^3/6}{\theta^2/2 } = \frac{3}{\theta} \to \infty, \ \ \theta \to 0 $$

Yani $\theta$ sıfıra yaklaşırken eğim neredeyse sonsuz, takip ettiğimiz nokta sağa, sola neredeyse hiç hareket etmiyor, neredeyse tüm hareket dikey şekilde. Demek ki şekil üzerindeki doğru cevap, dördüncü şekildir.

Problem 1E-4

$(0,1,2)$ ve $(2,0,3)$ noktalarından geçen çizgi düzlem $x + 4y + z = 4$'i nerede keser?

Cevap

A ve B noktaları üzerinden bir yön, yani bir vektör hesaplayabiliriz, $\vec{AB} = <2,-1,1>$. Sonra bu vektörün katları kadar, $t$ adımı atarak, başlangıç noktasından sonsuza kadar giden çizginin parametrik formülünü buluruz, yani $A + \vec{AB} \ t$.

$$ x = 0 + 2t = 2t $$

$$ y = 1 - t $$

$$ z = 2 + t $$

Parametrik formülü düzlem formülünde yerine koyalım.

$$ (2t) + 4(1-t) + (2+t) = 4 $$

Çözünce $t=2$ çıkar. Bunu parametrik formülde yerine koyunca $(4,-1,4)$ kesişim noktasını elde ederiz.

Problem 1E-5

$(1,1,-1)$ noktasından geçen çizgi $x+2y - z = 3$ düzlemine diktir. Bu çizgi $2x - y + z = 1$ düzlemini hangi noktada keser?

Cevap

Kesişim hesabı için çizginin parametrik denklemini bulmamız lazım. Eğer bu çizgi ilk düzleme dik ise, o düzlemin normalı "yönünde" gitmektedir, o zaman elimizde bir yön var, bir de başlangıç noktası var. O noktadan, normal yönünde $t$ adımı atmayı kodlayacağız (birinci düzlem ile kesişme önemli değil).

$$ x(t) = 1 + t $$

$$ y(t) = 1 + 2t $$

$$ z(t) = -1 -t $$

Şimdi bu çizginin ikinci düzlemle kesiştiği söylendiğine göre, şunun doğru olması gerekir

$$ 2(1+t) - (1+2t) + (-1-t) = 1 $$

Yani parametrik denklemin öğelerini teker teker ikinci düzlemin içine koymuş oluyoruz. Üstteki denklemi çözünce $t=-1$ çıkacak. Bunu alıp parametrik denkleme geri koyarsak, elde edilen nokta $(0,-1,0)$ noktasıdır [ders cevaplarında 0,1,0 deniyor, bu yanlış].

İki Boyutlu f(x,y) Fonksiyonunun Taylor Açılımı

Bir $f(x,y)$ fonksiyonunun Taylor açılımını yapmak için, daha önceden gördüğümüz tek boyutlu fonksiyon açılımından faydalanabiliriz [2].

Önce iki boyutlu fonksiyonu tek boyutlu olarak göstermek gerekir. Tek boyutta işleyen bir fonksiyon $F$ düşünelim ve bu $F$, arka planda iki boyutlu $f(x,y)$'ı kullanıyor olsun

Eğer

$$ f(x_0 +\Delta x, y_o + \Delta y) $$

fonksiyonun açılımını elde etmek istiyorsak, onu

$$ F(t) = f(x_0 + t\Delta x, y_o + t\Delta y) $$

üzerinden $t=1$ olduğu durumda hayal edebiliriz. $x,y$ parametrize olduğu için $f(x(t),y(t))$, yani

$$ x(t) = x_0 + t\Delta x $$

$$ y(t) = y_0 + t\Delta y $$

$F(t)$ bağlamında $x_o, y_o, \Delta x, \Delta y$ sabit olarak kabul edilecekler. Şimdi bildiğimiz tek boyutlu Taylor açılımını bu fonksiyon üzerinde, bir $t_0$ noktası yakınında yaparsak,

$$ F(t) = F(t_0) + F'(t_0)(t-t_0) + \frac{1}{2}F"(t_0)(t-t_0)^2 + ... $$

Eğer $t=1,t_0=0$ dersek

$$ F(1) = F(0) + F'(0) + \frac{1}{2}F"(0) + ... $$

olurdu. Bu iki değeri, yani $t=1,t_0=0$'i kullanmamızın sebepleri $t=1$ ile mesela $x_0 + t\Delta x$'in $x_0 + \Delta x$ olması, diğer yandan $t=0$ ile üstteki formülde $t$'nin yokolması, basit bir tek boyutlu açılım elde etmek.

Şimdi bize gereken $F',F"$ ifadelerini $x,y$ bağlamında elde edelim, ki bu diferansiyeller $F$'in $t$'ye göre birinci ve ikinci diferansiyelleri. Ama $F$'in içinde $x,y$ olduğu için açılımın Zincirleme Kanunu ile yapılması lazım.

$$ \frac{dF}{dt} = \frac{\partial F}{\partial x}\frac{\mathrm{d} x(t)}{\mathrm{d} t} + \frac{\partial F}{\partial y}\frac{\mathrm{d} y(t)}{\mathrm{d} t} $$

Ayrıca

$$ \frac{d}{dt}x(t) = \Delta x $$

$$ \frac{d}{dt}y(t) = \Delta y $$

olduğuna göre, tam diferansiyel daha da basitleşir

$$ \frac{\mathrm{d} F}{\mathrm{d} t} = \frac{\partial F}{\partial x}\Delta x + \frac{\partial F}{\partial y}\Delta y $$

Şimdi bu ifadenin bir tam diferansiyelini alacağız. Ama ondan önce şunu anlayalım ki üstteki ifade içinde mesela birinci terim de aslında bir fonksiyon, ve asıl hali

$$ \frac{\mathrm{d} F}{\mathrm{d} t} = \frac{\partial F(x(t),y(t))}{\partial x}\Delta x + ... $$

şeklinde. O zaman, bu terim üzerinde tam diferansiyel işlemini bir daha uyguladığımızda, Zincirleme Kanunu yine işleyecek, mesela üstte $\mathrm{d} x(t)/ \mathrm{d} t$'nin bir daha dışarı çıkması gerekecek. O zaman

$$ \frac{d^2F}{dt} = \bigg( \frac{\partial ^2 F}{\partial x^2}\frac{dx}{dt} + \frac{\partial ^2 F}{\partial x \partial y}\frac{dy}{dt} + \bigg) \Delta x + \bigg( \frac{\partial ^2 F}{\partial y \partial x}\frac{dy}{dt} + \frac{\partial ^2 F}{\partial y^2}\frac{dx}{dt} + \bigg) \Delta y $$

$$ = \bigg( \frac{\partial ^2 F}{\partial x^2}\Delta x + \frac{\partial ^2 F}{\partial x \partial y}\Delta y \bigg) \Delta x + \bigg( \frac{\partial ^2 F}{\partial y \partial x}\Delta x + \frac{\partial ^2 F}{\partial y^2}\Delta y \bigg) \Delta y $$

$$ = \bigg( \frac{\partial ^2 F}{\partial x^2}\Delta x^2 + \frac{\partial ^2 F}{\partial x \partial y}\Delta y \Delta x \bigg) + \bigg( \frac{\partial ^2 F}{\partial y \partial x}\Delta x \Delta y + \frac{\partial ^2 F}{\partial y^2}\Delta y^2 \bigg) $$

Kalkülüs'ten biliyoruz ki

$$ \frac{\partial ^2 F}{\partial x \partial y} = \frac{\partial ^2 F}{\partial y \partial x} $$

Daha kısa gösterimle

$$ f_{xy} = f_{yx} $$

Yani kısmi türevin alınma sırası farketmiyor. O zaman, ve her şeyi daha kısa gösterimle bir daha yazarsak

$$ = (f_{xx}\Delta x^2 + f_{xy}\Delta y \Delta x ) + (f_{xy}\Delta x \Delta y + f_{yy}\Delta y^2 ) $$

$$ \frac{d^2F}{dt} = (f_{xx}\Delta x^2 + 2f_{xy}\Delta y \Delta x + f_{yy}\Delta y^2 ) $$

Artık elimizde $F$ ve $F'$ var, bunları

$$ F(1) = F(0) + F'(0) + \frac{1}{2}F"(0) + ... $$

içine yerleştirebiliriz. En son şu kaldı, $F(0)$ nedir? $F$'in $t=0$ olduğu anda değeridir,

$$ F(t) = f(x_0 + t\Delta x, y_o + t\Delta y) $$

$$ F(0) = f(x_0 + 0 \cdot \Delta x, y_o + 0 \cdot \Delta y) $$

$$ = f(x_0 , y_o) $$

Benzer şekilde, tüm türevler de $t=0$ noktasında kullanılacaktır, o zaman onlar da

$$ F'(0) = f_x(x_0,y_0) \Delta x + f_y(x_0,y_0) \Delta y $$

$$ F"(0) =
f_{xx}(x_0,y_0)\Delta x^2 + 2f_{xy}(x_0,y_0)\Delta y \Delta x + f_{yy}(x_0,y_0)\Delta y^2 $$

şeklinde olurlar. Tamam. Şimdi ana formülde yerlerine koyalım,

$$ \begin{array}{lll} F(1) &=& f(x_0 +\Delta x, y_o + \Delta y) \\ \\ &=& f(x_0 , y_o) + f_x(x_0,y_0) \Delta x + f_y(x_0,y_0) \Delta y + \\ \\ && \frac{1}{2} [ f_{xx}(x_0,y_0)\Delta x^2 + 2f_{xy}(x_0,y_0)\Delta y \Delta x + f_{yy}(x_0,y_0)\Delta y^2 ] + ... \end{array} $$

Çok Boyutlu Taylor Açılımı

Bir $h$ adımı için, $\bar{x}$ noktasındaki Taylor açılımı,

$$ f(x + h) = f(\bar{x}) + \nabla f(\bar{x}) h + \frac{1}{2} h^T \nabla^2f(\bar{x}) h + ... $$

Çizgi Düzlem Kesişmesi

Elimizde $P = 2x + y - 4z = 4$ düzlemi var. Bu düzlemin

$$ x = t \quad y = 2 + 3t \quad z = t$$

çizgisi ile kesiştiği yer neresidir?

Cevap kolay; çizgi denkleminde $t$ bazlı tanımlı $x,y,z$ değerleri $P$'ye sokarsak, tek bilinmeyeni $t$ olan bir denklem çıkar,

$$ 2(t) + (2+3t)-4(t) = 4 \Rightarrow t = 2$$

Çizgi Düzlem Kesişmesini Vektörler ile Hesaplamak

Üstteki yöntem cebirsel manipülasyon gerektiriyor, fakat sayısal hesap için sembolik cebir işlemlerine girmeden vektör matematiği ile direk bir sonuç bulamaz mıyız? [1,4]'ü temel alalım: alttaki durumu düşünelim,

Grafiğe göre $P(s)$ $P_1$ ve $P_0$ arasındaki birim vektörün $s$ kadar uzatılmış hali olsun, o aralığı $u$ kabul edersek $P(s)-V_0 = w + su$ olur. Düzlem ile kesişmenin olduğu noktayı $P(s_I)$ diye tanımlayalım, aradığımız nokta burası. O noktada $n$ ile $P(s_I)$ dikgen olacaktır, yani $P(s) - V_0 = w + su$ vektörü $n$'e dikgen olacaktır, ki $w=P_0-V_0$. Bu durumda $n \cdot (w+su) = 0$ olur. Bunu kullanarak,

$$ s_I = \frac{-n \cdot w}{n \cdot u} = \frac{n \cdot (V_0 - P_0)}{n \cdot (P_1-P_0)} = \frac{-(ax_0 + by_0 + cz_0 + d)}{n \cdot u} $$

n = np.array([1., 1., 1.])
V0 = np.array([1., 1., -5.])
P0 = np.array([-5., 1., -1.])
P1 = np.array([1., 2., 3.])

w = P0 - V0;
u = P1-P0;
N = -np.dot(n,w);
D = np.dot(n,u)
sI = N / D
I = P0+ sI*u
print I

[-3.90909091  1.18181818 -0.27272727]

Grafiklersek

import sys; sys.path.append('../../vision/vision_02')
import plot3d

f = plt.figure()
ax = f.gca(projection='3d')
w = 10
ax.set_xlim(-w,w);ax.set_ylim(-w,w);ax.set_zlim(-w,w)
ax.set_xlabel("X")
ax.set_ylabel("Y")
ax.set_zlabel("Z")
v = P1-P0
ax.quiver(P0[0], P0[1], P0[2], v[0], v[1], v[2], color='red')
ax.scatter(V0[0], V0[1], V0[2], color='black')
ax.scatter(V0[0]+n[0], V0[1]+n[1], V0[2]+n[2], color='black')
ax.scatter(I[0], I[1], I[2], color='black')
ax.quiver(V0[0], V0[1], V0[2], n[0], n[1], n[2], color='blue')
plot3d.plot_plane(ax, list(V0), list(n), color='y')
plt.savefig('5_10.png')

Çizgi Parçasına Noktanın En Yakın Mesafesi

Elimizde verili iki nokta arasında tanımlı çizgi parçası var. Herhangi bir noktanın bu parçaya en yakın mesafesi nedir? Ayrıca o noktadan parçaya bir düz çizgi çekilse kesişimin olduğu nokta nerededir?

Şu metota bakalım [5]. Çizgiyi $\vec{z} = \vec{a} + t \vec{b}$ olarak tanımlayabiliriz. O zaman bu çizgi ile bir diğer nokta $\vec{x}$ arasındaki mesafe $\vec{x}-\vec{z}$ vektörünün uzunluğudur, yani

$$ || \vec{x} - (\vec{a} + t' \vec{b}) || $$

olarak tanımlanabilir, ki burada $t'$ özel bir $t$ değeri oluyor. Bu değer öyle bir $t$ değeri ki o noktaya kadar gelen $\vec{z}$'nin bolumu $\vec{x}$'e dik. Bu noktayı ve ardından çizgiye olan (dik) mesafeyi nasıl buluruz?

Şimdi üstteki çizgi formülünde kesişim anına kadar olan bölümdeki, $t'$'ye tekabül eden kısma $\vec{r}$ diyelim, ve onu

$$ \vec{r} = \vec{a} + t' \vec{b} $$

olarak gösterelim. İstediğimiz $||\vec{r}-\vec{x}||$ uzunluğunu bulmak. $t'$ değerinde aradaki vektör $\vec{b}$'ye dik olduğuna göre

$$ (\vec{x} - \vec{r}) \cdot \vec{b} = 0 $$

$\vec{r}$ formülünü açalım,

$$ = (\vec{x} - \vec{a} - t' \vec{b}) \cdot \vec{b} = 0 $$

$$ = \vec{x}\cdot\vec{b} - \vec{a}\cdot\vec{b} - t'||b||^2 = 0 $$

$$ t' = \frac{\vec{x}\cdot\vec{b} - \vec{a}\cdot\vec{b}}{||b||^2} $$

Örnek

$< 2,2 >$ ve $< 5,5 >$ noktaları noktalarından geçen çizgiye $< 4,1 >$ noktasının uzaklığı nedir? Kesişim nerede olur?

def dist(x1,y1,x2,y2,px,py):
    a = np.array([[x1,y1]]).T
    b = np.array([[x2,y2]]).T
    x = np.array([[px,py]]).T
    tp = (np.dot(x.T, b) - np.dot(a.T, b)) / np.dot(b.T, b)
    tp = tp[0][0]
    tmp = x - (a + tp*b)
    d = np.sqrt(np.dot(tmp.T,tmp)[0][0])
    return d, a+tp*b

x1,y1=2.,2.
x2,y2=5.,5.
px,py=4.,1.

d, inters = dist(x1,y1, x2,y2, px,py)
print (d)
print (inters)

2.1213203435596424
[[2.5]
 [2.5]]

Not: Üstteki metot 2, 3 üzeri boyutlar için de işleyecektir.

İki Nokta Arasında Parametrize Edilmiş Eğri

Diyelim ki $(1,1)$ ve $(4,4)$ noktalarından geçen ve dışarıdan tanımlı parametrelerle yeterince eğilip, bükülebilecek bir eğri tanımlamamız lazım. Polinomlar üzerinden tanımlanan bir eğri ile bunu başarabiliriz,

$$ x(t) = a_0 + a_1 t + a_2 t^2 + a_3 t^3 $$

$$ y(t) = b_0 + b_1 t + b_2 t^2 + b_3 t^3 $$

Bu şekilde bir eğri yeterince eğilip bükülebilir, ve istenen şekle sokulabilir. Fakat baş ve sonun verili noktalardan geçmesini nasıl garanti ederiz? Bunun için bu noktaları üstteki denkleme sokalim, ve $0 \le t \le 1$ olacak sekilde kısıtlama yapalim, $t=0$'da

$$ 1 = a_0 + a_1 (0) + a_2 (0)^2 + a_3 (0)^3 $$

$$ 1 = b_0 + b_1 (0) + b_2 (0)^2 + b_3 (0)^3 $$

Yani $a_0=1$ ve $b_0=1$. Peki $t=1$ icin?

$$ 4 = 1 + a_1 (1) + a_2 (1)^2 + a_3 (1)^3 $$

$$ 4 = 1 + b_1 (1) + b_2 (1)^2 + b_3 (1)^3 $$

$$ 3 = a_1 + a_2 + a_3, \quad 3 = b_1 + b_2 + b_3 $$

Demek ki üstteki iki formüle mutabık kaldığımız sürece $a_1,a_2,a_3,b_1,b_2,b_3$ ie istediğimiz şekilde oynayarak istediğimiz eğriyi ortaya çıkartabiliriz.

t = np.linspace(0,1.0,100)

a1,a2 = -1.1, 1.9
b1,b2 = 1.1, 1.4

sx,sy=(1.0,1.0)
ex,ey=(4.0,4.0)

a3 = ex - sx - (a1+a2)
b3 = ey - sy - (b1+b2)

x = 1.0 + a1*t + a2*t**2 + a3*t**3
y = 1.0 + b1*t + b2*t**2 + b3*t**3

plt.xlim(0,5.0)
plt.ylim(0,5.0)
plt.plot(x,y)
plt.savefig('5_11.png')

Max ve Sigmoid Bazlı Yaklaşım

Daha önce [6]'da görülen spline tekniğinin parametrik hali de olabilir. Mesela

a1,b1,c1,d1 = (1, -1.4, 2, 2.5)
a2,b2,c2,d2 = (1, 1.4, 1, 2.5)
def f(t):
    x = ax + \
        bx*np.max([0,t-2]) + \
        cx*np.max([0,t-3]) + \
        dx*np.max([0,t-4])

    y = ay + \
        by*np.max([0,t-2]) + \
        cy*np.max([0,t-3]) + \
        dy*np.max([0,t-4])
    return x,y     

tmp = np.linspace(0,5,100)
res = np.array([f(tt) for tt in tmp])
plt.plot(res[:,0],res[:,1])
plt.savefig('5_12.png')

Başlangıcı $a_x,a_y$ olan kesik bir eğriyi görüyoruz. Bu tür eğrileri aynen [6]'da olduğu gibi sigmoid bazlı yapabiliriz,

rho = 7.0
def sig(x,a):
   return (x-a)*1/(1+np.exp(-rho*(x-a)))

def maxk(x,a):
   return np.max([0,x-a])

ax,bx,cx,dx,ex = (1, 2.4, 1, -3.5, -2.1)
ay,by,cy,dy,ey = (1, 0.4, -0.1, 0.5, -3)
def f(t):
    x = ax + \
        bx*maxk(t,2) + \
        cx*maxk(t,3) + \
        dx*maxk(t,3.5) + \
        ex*maxk(t,4.0)

    y = ay + \
        by*maxk(t,2) + \
        cy*maxk(t,3) + \
        dy*maxk(t,3.5) + \
        ey*maxk(t,4.0)
    return x,y     

def g(t):
    x = ax + \
        bx*sig(t,2) + \
        cx*sig(t,3) + \
        dx*sig(t,3.5) + \
        ex*sig(t,4.0)

    y = ay + \
        by*sig(t,2) + \
        cy*sig(t,3) + \
        dy*sig(t,3.5) + \
        ey*sig(t,4.0)
    return x,y     

tmp = np.linspace(0,5,100)

res = np.array([f(tt) for tt in tmp])
plt.plot(res[:,0],res[:,1])
plt.savefig('5_13.png')

res = np.array([g(tt) for tt in tmp])
plt.plot(res[:,0],res[:,1])
plt.savefig('5_14.png')

Herhangi bir şekli katsayılarla yaratmak mümkün.

Bitiş noktalasını nasıl ayarlarız? Burada yine polinom örnekteki gibi cebirsel bir yöntem seçebilirdik, fakat çoğunlukla başlangıç ve bitiş arasındaki eğriler bir optimizasyon bağlamında kullanılır. Bu durumda bitiş noktaları ile katsayılar arasında bir optimizasyon kısıtlaması yaratmak ve bitiş noktalarını böyle ayarlamak daha iyidir.

Çünkü biliyoruz parametrize ortamda mesela önceki örnekte $0 \ge t \ge 5$. O zaman egrinin bitisinde $t=5$ olacağını biliyoruz. Bu durumda mesela

$$ x = a_x + \ b_x \sigma(t,2) + \ c_x \sigma(t,3) + \ d_x \sigma(t,3.5) + e_x \sigma(t,4.0) $$

ifadesine $t$ tüm ilmik noktalarının ötesinde olduğu için artık tüm $\sigma$ ifadeleri 1 veriyor. Eğer 1 veriyorsa, yani tüm sigmoid'ler aktif ise, eğri bitişinde bilinen $t$ üzerinden elimizdeki $x$ $x = a_x + b_x(5-2) + c_x(5-3) + d_x(5-3.5) + e_x(5-4.0)$ olmalı. Optimizasyonda bu eşitliğin belli bir değer (istediğimiz bitiş noktası kordinatı) olmasını şart tutarak amacımız erişebiliriz.

Kaynaklar

[1] Sunday, Intersection of Lines and Planes, http://geomalgorithms.com/a05-_intersect-1.html

[2] Feldman, Taylor Polynomials in Dimension Two, http://www.math.ubc.ca/~feldman/m200/taylor2dSlides.pdf

[3] Thomas, Thomas' Calculus

[4] Khaled, Straight Line and Plane Intersection Matlab Code, https://uk.mathworks.com/matlabcentral/fileexchange/17751-straight-line-and-plane-intersection

[5] Distance between Point and Line, https://brilliant.org/wiki/distance-between-point-and-line/

[6] Bayramlı, Hesapsal Bilim, Spline Eğrileri ve Baz Fonksiyonlar