Oyun Teorisi ile Grup Kararları Tahmini
Bruce de Mesquita mutabakata / anlaşmaya varma / savaş konularında tahminler yapabilen bir araştırmacı. Girdi olarak alttaki gibi bir veriyi alıp,
import pandas as pd
dfemis = pd.read_csv('emission.csv'); print dfemis
Actor Capability Position Salience
0 Netherlands 0.08 4 80
1 Belgium 0.08 7 40
2 Luxembourg 0.03 4 20
3 Germany 0.16 4 80
4 France 0.16 10 60
5 Italy 0.16 10 60
6 UK 0.16 10 90
7 Ireland 0.05 7 10
8 Denmark 0.05 4 100
9 Greece 0.08 7 70
onu hangi mutabakatın olacağı tahmini için kullanabiliyor. Üstteki veri bazı ülkeler arasında orta boy arabalarda emisyon kontrolünü kaç sene sonra devreye sokulacağı hakkında bir grup kararı. BDM'nin bu hesabı yapmak için iki yöntemi var, birincisi yarı-Oyun Teorisel (quasi Game Theoretic), ikincisi tam Oyun Teorik (ve daha kuvvetli bazı özellikleri var). Birinci model hakkında daha çok dokümantasyon var, bu model ile BDM pek çok başarılı tahmine de imza attı bu arada. Bu yazıda paylaşacağımız birinci model ve onun kodlaması.
Veride güç / beceri (capability), ve ilgi (salience) parametreleri var. Bunların ne olduğu belli. Pozisyon üzerinde anlaşmazlık olan şeydir, her türlü karar ilginç bir şekilde tek boyutlu bir skala üzerinden temsil edilebiliyor, yani bir şey hiç istememek 0, çok istemek 100, ve arada tüm seçimler aradaki değerler olabilir. Çok / az istemek arasındaki her nokta belli seçenek kombinasyonlarını bile barındırıyor olabilir.
Oyunun sonucu "evreler" üzerinden işlenir. Her evrede aktörler güçleri oranında diğer aktörleri kendi pozisyonlarına davet ediyorlar, ya da etmiyorlar. Bir evrede her aktör pek çok diğer aktörden "benim yanıma gel" isteği almış olabilir, evre sonunda aktör bu tekliflerden (offer) kendisi için en az değişim gerektirecek seçeneğe gidiyor (ilk başlangıç noktasına göre, bir öncekine göre değil). Hoca bunu bu şekilde seçmiş ve iyi bir seçim bizce çünkü doğa enerji israfını sevmez. İnsanlar da öyle!
Ortalamalar
Bir oyunun, herhangi bir evresi için, ağırlıklı ortalama ve ağırlıklı doruğu (mode) hesaplanabilir. Ağırlıklı çünkü herkesin pozisyonunun basit ortalaması değil, kişilerin ilgi ve gücü ile orantılı bir ortalama. Ağırlıklı ortalama için formül
$$ \frac{\sum_{i=1}^{n} c_i s_i x_i}{\sum_{i=1}^{n} c_i s_i} $$
Ağırlıklı doruk için biraz takla lazım, önce tüm veriyi pozisyonlara göre sıralarız, herkesin $c_is_i$ çarpımını hesaplayıp normalize ederiz, ve kümülatif olarak bu rakamları toplarız. Hangi noktada 0.5'e erişilmiş ise o nokta "ağırlıklı orta" oluyor, ve o noktanın pozisyonu doruk olarak kabul ediliyor. Hatırlanabileceği üzere basit doruk hesabı için, yani düz bir liste sayı için, o sayılar sıralanıyordu, ve ortadaki sayı mode olarak seçiliyordu. Burada aynı kavram sadece $c_i,s_i$ işin içinde.
import scholz
dfiran.Salience = dfiran.Salience/100.
game = scholz.Game(dfiran)
print 'ortalama', game.mean()
print 'mode', game.weighted_median()
ortalama 54.3833734112
mode 50.0
Her evrede hesaplanan ana formüller şunlar,
$$ E(U_{ij}|\textrm{teklif et}) = (1-s_j)U_{si} + s_jP_i^i U_{si} + s_j(1-P_i^i)U_{fi} $$
$$ E(U_{ij}|\textrm{teklif etme}) = QU_{sq} + (1-Q) \big( T U_{bi}) + (1-T)U_{wi} \big)$$
$$ E(U_{ij}) = E(U_{ij}|\textrm{teklif et}) - E(U_{ij}|\textrm{teklif etme}) $$
Teklif etmek bir diğer oyuncuyu pozisyonunu değiştirmesi için iknaya uğraşmak / ona "sormak" (challange). Formülerin bileşenlerini altta açacağız. Önce genel faydadan başlayalım. Fayda (utility) $U_{ij}^i$ aktör $i$'nin kendi pozisyonuna benzerliğe verdiği değerdir, diğer aktör $j$ uzaksa buna atanan fayda az, yakınsa çoktur.
$$ U_{ij}^i = 1-2 \bigg| \frac{x_i - x_j}{x_{max}-x_{min}}\bigg| $$
$U_{ii}^i$ doğal olarak 1 değerinde, aktör kendi pozisyonunda en çok faydayı görüyor.
Bir aktör bir diğer aktörü iknaya uğraşabilir. Bu durumda elde edeceği fayda -başarılı olursa- aktörün kendi pozisyon faydası ve diğerinin arasındaki uzaklığa oranlı görülebilir. Yani bana en uzak pozisiyondaki birini ikna etmek bana en çok fayda getirir, daha yakın, daha az. Her aktörün içinde olduğu risk $ 0 \le r_i \le 1$ olacak şekilde (ki risk ile ne denmek istediğini ileride anlatacağız),
$$ U_{si}^i = 2 - 4 \bigg[ \frac{2-(U_{ii}^i - U_{ij}^i)}{4} \bigg]^{r_i}$$
Kaybetme durumunda kaybedilen fayda $U_{fi}^i$ ise üstteki faydalar çıkartmalarının ters çevirilmiş hali olarak düşünebilirim, bir anlamda ikna edilmiş olma durumu olabilir bu, ikna ettiğimde kazandığıma göre edildiğimde kaybederim, ve bu çıkarma işleminin ters çevirilmiş hali gibi görülebilir, yani $ U_{ij}^i - U_{ii}^i$, o zaman
$$ U_{fi}^i = 2 - 4 \bigg[ \frac{2-(U_{ij}^i - U_{ii}^i)}{4} \bigg]^{r_i}$$
$U_{ij}^i$ formülünü üstteki iki formüle sokarsak, ve $U_{ii}^i=1$ olduğuna göre, basitleştirdikten sonra,
$$ U_{si}^i = 2 - 4 \bigg[ 0.5 - 0.5 \bigg| \frac{x_i-x_j}{x_{max}-x_{min}} \bigg| \bigg]^{r_i} $$
$$ U_{fi}^i = 2 - 4 \bigg[ 0.5 - 0.5 \bigg| \frac{x_j-x_i}{x_{max}-x_{min}} \bigg| \bigg]^{r_i} $$
elde ederim.
Yarışma
Nihai hesap için aktörler arasındaki muhtemel bir yarışta kim üstte kalır, bunu hesaplamamız gerekiyor. Bu ölçütü $v_i^{jk}$ ile gösterebilirim, yani aktör $i$ eğer aktörler $j,k$ arasında seçim yapması gerekirse kimi tercih eder? Daha doğrusu, $i$'nin oyu (vote) ne olur? Bunun formülü,
$$ v_i^{jk} = c_is_i (U_{ij} - U_{ik}) $$
olarak gösterilebilir.
import pandas as pd
import numpy as np
Q = 1.0 ; T = 1.0
class Game:
def __init__(self,df):
self.df = df.copy()
self.df_orig = self.df.copy()
# dictionaries of df variables - used for speedy access
self.df_capability = df.Capability.to_dict()
self.df_position = df.Position.to_dict()
self.df_salience = df.Salience.to_dict()
self.max_pos = df.Position.max()
self.min_pos = df.Position.min()
def weighted_median(self):
df = self.df.copy()
df['w'] = df.Capability*df.Salience
df = df.sort_index(by='Position',ascending=True)
df['w'] = df['w'] / df['w'].sum()
df['w'] = df['w'].cumsum()
return float(df[df['w']>=0.5].head(1).Position)
def mean(self):
return (self.df.Capability*self.df.Position*self.df.Salience).sum() / \
(self.df.Capability*self.df.Salience).sum()
print 'v'
print game.v(1,0,2)
print game.v(0,1,2)
print game.v(0,2,3)
v
63.1578947368
84.2105263158
94.7368421053
Kabiliyet ve ilgi ile çarpmak mantıklı herhalde, çünkü aktörün oyunu hesaplıyoruz, bu oy aktörün gücüne oranlı olmalı. Hesapta $i$ aktörünün $j$'den elde edeceği faydayı $j$ faydasından çıkartıyoruz. $j$ solda olduğu için bu hesap, artı sayılar bağlamında, $i$'nin $j$'yi tercihi olarak ta görülebilir, eğer $j$'ye verilen tüm oyları hesaplamak istersek, o zaman her $i$ için yapılan $v_i^{jk}$'leri toplayıp bölümde kullanmalıyız, ve bölümde ise $j$'den gelen faydanın daha fazla olduğu oyları kullanmalıyız,
$$ P^j = \sum_{ U_{ij} > U_{ik} } v_i^{jk} \bigg/ \sum_i \big| v_i^{jk} \big| $$
İndiste $j$ kullanımı biraz garip oldu, genellikle eşitliğin sol tarafında $i$ kullanmaya alıştık, ufak bir indis değişimi yapalım,
$$ P^i = \sum_{ U_{ji} > U_{jk} } v_j^{ik} \bigg/ \sum_j \big| v_j^{ik} \big| $$
Üstteki hesap "kim benimle beraber" hesabı olarak ta görülebilir. Eğer daha fazla aktör bu kişiyle beraber ise (bölümdeki kısım), bu durum herhangi bir ikili çarpışmada üstte kalınabileceği anlamına gelir.
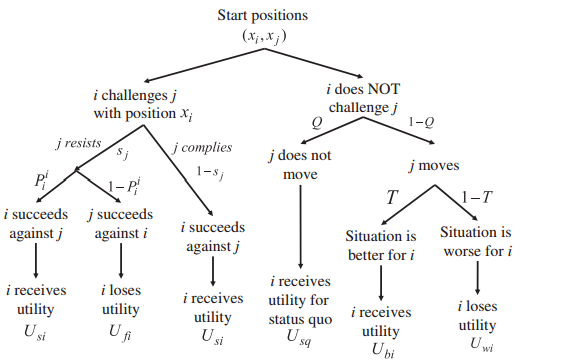
Alttaki "oyun ağacı (game tree)" şöyle okunabilir, ana beklenti formülleri bu ağacın "düzleştirilmiş" hali bir bakıma. Her seçenek, seçilebilecek her yol o yolun olasılığı ve nihai uç değeri ile çarpılıp toplanıyor.
from __future__ import division
import csv
class Actor(object):
def __init__(self, name, model, x, c, s):
self.name = name
self.x = x
self.c = c
self.s = s
self.r = 1
self.basic_utilities = {}
self.probs = {}
self.expected_utilities = {}
self.offers = []
def calculate_utilities(self, alter):
dx = self.model.xmax - self.model.xmin
mu = self.model.mu
Us = 2 - 4*(0.5 - 0.5*abs((self.x - alter.x)/(dx)))**int(self.r)
Uf = 2 - 4*(0.5 + 0.5*abs((self.x - alter.x)/(dx)))**int(self.r)
Ub = 2 - 4*(0.5 - 0.25*((abs(self.x - mu)+abs(self.x-alter.x))/dx)) \
**int(self.r)
Uw = 2 - 4*(0.5 + 0.25*((abs(self.x - mu)+abs(self.x-alter.x))/dx)) \
**int(self.r)
Usq = 2 - 4*0.5**self.r
self.basic_utilities[alter.name] = {"Us": Us,
"Uf": Uf,
"Ub": Ub,
"Uw": Uw,
"Usq": Usq}
def calculate_prob(self, alter):
if self.x == alter.x:
self.probs[alter.name] = 0
return
top = 0
bottom = 0
for agent in self.model.Actors:
d = abs(agent.x - alter.x) - abs(agent.x - self.x)
top += agent.c * agent.s * d
bottom += agent.c * agent.s * abs(d)
top = max(top, 0)
self.probs[alter.name] = top/bottom
def calculate_expected_utility(self, alter):
p = self.probs[alter.name]
utils = self.basic_utilities[alter.name]
Q = self.model.Q
T = self.model.T
s = alter.s
EU = s * (p * utils["Us"] + (1-p)*utils["Uf"]) + (1-s)*utils["Us"]
EU -= Q*utils["Usq"] - (1-Q)*(T*utils["Ub"] + (1-T)*utils["Uw"])
self.expected_utilities[alter.name] = EU
def calculate_r(self):
attack_utils = [alter.expected_utilities[self.name]
for alter in self.model.Actors if alter is not self]
security_levels = []
for actor in self.model.Actors:
security = sum([alter.expected_utilities[actor.name]
for alter in self.model.Actors if alter is not actor])
security_levels.append(security)
max_security = max(security_levels)
min_security = min(security_levels)
R = (2 * sum(attack_utils) - max_security - min_security) / \
max(0.001,(max_security - min_security))
self.r = (1 - R/3)/(1+R/3)
def send_offers(self):
for actor in self.model.Actors:
if actor.name in self.expected_utilities:
if self.expected_utilities[actor.name] > 0:
# Send a challenge!
offer = {"Sender": self.name,
"x": self.x, # Target position
"EU": self.expected_utilities[actor.name]
}
actor.offers.append(offer)
def choose_offer(self):
if len(self.offers) == 0: return
max_util = max([offer["EU"] for offer in self.offers])
self.offers = [offer for offer in self.offers if offer["EU"] == max_util]
offer = min(self.offers, key=lambda x: abs(self.x-x["x"]))
# Resolve offer
Uj = offer["EU"]
Ui = self.expected_utilities[offer["Sender"]]
if Ui > 0 and Ui < Uj:
# There was a conflict, and this actor lost
print self.name + " kaybediyor " + offer["Sender"]
self.x = offer["x"]
# If the actor won the conflict, action will be taken on the other end
elif Ui < 0 and abs(Ui) < Uj:
# Compromise
print self.name + " orta noktada anlasiyor " + offer["Sender"]
self.x += (offer["x"] - self.x) * abs(Ui/Uj)
elif Ui < 0 and abs(Ui) > Uj:
# Capituate
print self.name + " tarafina geciyor " + offer["Sender"]
self.x = offer["x"]
self.offers = [] # Reset offers
class Model(object):
def __init__(self, Actors, xmax, xmin, Q=1.0, T=1.0):
self.Actors = Actors
for actor in self.Actors:
actor.model = self
self.xmax = xmax
self.xmin = xmin
self.dx = xmax - xmin
self.mu = 0 # Current median position
self.Q = Q
self.T = T
self.actor = {actor.name: actor for actor in self.Actors}
def vote(self, verbose=False):
pairwise_contests = {}
for j in self.Actors:
for k in self.Actors:
votes = 0
for i in self.Actors:
votes += i.c*i.s*((abs(i.x - k.x) - abs(i.x - j.x))/(self.dx))
pairwise_contests[(j.x, k.x)] = votes
if verbose:
for key, val in pairwise_contests.items():
print key, val
return max(pairwise_contests, key=lambda x: pairwise_contests[x])[0]
def find_mean(self):
t = 0 # Running weighted total
w = 0 # Running total weight
for actor in self.Actors:
w += actor.s * actor.c
t += actor.s * actor.c * actor.x
return t/w
def calculate_basic_utilities(self):
for actor in self.Actors:
for alter in self.Actors:
if actor is not alter:
actor.calculate_utilities(alter)
def calculate_win_probabilities(self):
for actor in self.Actors:
for alter in self.Actors:
if actor is not alter:
actor.calculate_prob(alter)
def calculate_expected_utilities(self):
for actor in self.Actors:
for alter in self.Actors:
if actor is not alter:
actor.calculate_expected_utility(alter)
def calculate_r(self):
for actor in self.Actors:
actor.calculate_r()
def make_offers(self):
for actor in self.Actors:
actor.send_offers()
def resolve_offers(self):
for actor in self.Actors:
actor.choose_offer()
def run_model(self):
for actor in self.Actors:
actor.r = 1
self.mu = self.vote(False)
self.calculate_basic_utilities()
self.calculate_win_probabilities()
self.calculate_expected_utilities()
self.calculate_r()
self.mu = self.find_mean()
self.calculate_basic_utilities()
self.calculate_win_probabilities()
self.calculate_expected_utilities()
self.make_offers()
self.resolve_offers()
def run(csv_file, iter=10, xmin=1, xmax=10,T=1.0,Q=1.0):
with open(csv_file, 'rU') as f:
reader = csv.DictReader(f, )
actors = [actor for actor in reader]
for actor in actors:
for key in actor:
try:
actor[key] = float(actor[key])
except:
continue
Actors = []
for actor in actors:
new_actor = Actor(actor["Actor"],
None,
actor["Position"],
actor["Capability"],
actor["Salience"]/100.0)
Actors.append(new_actor)
model = Model(Actors, xmax, xmin)
for actor in model.Actors:
actor.model = model
model.T = T
model.Q = Q
model.vote()
model.find_mean()
[actor.x for actor in model.Actors]
for i in range(iter):
model.run_model()
print model.vote(False)
Bu yaklaşımı örnek olarak 1998'de Britanya'nın Avro para birliğine girip girmeyeceği kararı üzerinde uygulayalım [6]. Alttaki değerler İşçi Partisinin iktidarda olduğu senaryosuna göre seçilmiş, Muhafazakar iktidarı seçeneğinde sadece aktörlerin gücü / etkileri değişiyor, pozisyonlar her iki durumda da aynı. Skalada güç 0-1 arası, pozisyon 0-10.
import pandas as pd
dfuk = pd.read_csv('uk_emu_labor.csv'); print dfuk
Actor Capability Position Salience
0 Isci Partisi (Avrocu) 1.0 8 40
1 Isci Partisi (AB Karsiti) 0.5 4 40
2 Ingiliz Merkez Bankasi 0.1 5 60
3 Teknokratlar 0.1 10 40
4 Sanayiciler 0.1 5 40
5 Direktorler Enstitusu 0.1 4 40
6 Finanscilar 0.1 9 60
7 Muhafazakar AB Karsiti 0.3 1 95
8 Muhafazakar AB Taraftari 0.3 6 50
Oyunu isletince sonuc,
import bdm
bdm.run("uk_emu_labor.csv",iter=5)
Isci Partisi (Avrocu) tarafina geciyor Sanayiciler
Isci Partisi (AB Karsiti) tarafina geciyor Finanscilar
Teknokratlar tarafina geciyor Sanayiciler
Direktorler Enstitusu tarafina geciyor Finanscilar
Finanscilar kaybediyor Sanayiciler
Muhafazakar AB Karsiti tarafina geciyor Sanayiciler
5.0
Isci Partisi (AB Karsiti) tarafina geciyor Isci Partisi (Avrocu)
Direktorler Enstitusu tarafina geciyor Isci Partisi (Avrocu)
5.0
5.0
5.0
5.0
5 değeri çıktı, ki bu [6]'daki sonuca yakın. Eğer Muhafazakar Parti iktidarına göre işletirsek,
import bdm
bdm.run("uk_emu_cons.csv",iter=5)
Isci Partisi (Avrocu) tarafina geciyor Ingiliz Merkez Bankasi
Isci Partisi (AB Karsiti) tarafina geciyor Ingiliz Merkez Bankasi
Teknokratlar tarafina geciyor Ingiliz Merkez Bankasi
Direktorler Enstitusu tarafina geciyor Ingiliz Merkez Bankasi
Finanscilar tarafina geciyor Ingiliz Merkez Bankasi
Muhafazakar AB Taraftari tarafina geciyor Ingiliz Merkez Bankasi
1.0
Isci Partisi (Avrocu) tarafina geciyor Muhafazakar AB Karsiti
Isci Partisi (AB Karsiti) tarafina geciyor Muhafazakar AB Karsiti
Teknokratlar tarafina geciyor Muhafazakar AB Karsiti
Sanayiciler tarafina geciyor Muhafazakar AB Karsiti
Direktorler Enstitusu tarafina geciyor Muhafazakar AB Karsiti
1.0
Ingiliz Merkez Bankasi tarafina geciyor Muhafazakar AB Karsiti
Finanscilar tarafina geciyor Muhafazakar AB Karsiti
Muhafazakar AB Taraftari tarafina geciyor Muhafazakar AB Karsiti
1.0
1.0
1.0
Sonuç 1, yani Avro'ya hiç destek yok. Bu pek beklenmez bir durum değil, çünkü İngiltere'de Muhafazakarlar AB'ye zaten soğuk dururlar. Tarihten biliyoruz ki Britanya Avro'ya girmedi, hatta bilindiği gibi 2016'da referandumda AB'den çıkma kararı aldı!
Ödev: Britanya'nın AB'den çıkışını (Brexit) tahmini. Mesquita'ya göre metotu için gereken ham veriyi yeterince haberleri izleyen herhangi biri yaratabilir. Aktörler herhalde üstteki örneğe yakın olur, halkın seçiminin bu aktörlerin seçimini yansıttığı varsayılabilir. Sonuç ne olur?
İlk baştaki emisyon örneği,
import bdm
bdm.run("emission.csv",iter=10,xmin=4)
Belgium tarafina geciyor France
Luxembourg orta noktada anlasiyor France
Ireland tarafina geciyor France
10.0
Belgium tarafina geciyor Netherlands
Luxembourg tarafina geciyor Netherlands
Ireland orta noktada anlasiyor Netherlands
7.0
Belgium tarafina geciyor France
Luxembourg tarafina geciyor France
Ireland orta noktada anlasiyor France
10.0
Belgium tarafina geciyor Netherlands
Luxembourg tarafina geciyor Netherlands
Ireland tarafina geciyor Netherlands
7.0
Belgium tarafina geciyor France
Luxembourg tarafina geciyor France
Ireland orta noktada anlasiyor France
10.0
Belgium tarafina geciyor Netherlands
Luxembourg tarafina geciyor Netherlands
Ireland tarafina geciyor Netherlands
7.0
Belgium tarafina geciyor France
Luxembourg tarafina geciyor France
Ireland orta noktada anlasiyor France
10.0
Belgium tarafina geciyor Netherlands
Luxembourg tarafina geciyor Netherlands
Ireland tarafina geciyor Netherlands
7.0
Belgium tarafina geciyor France
Luxembourg tarafina geciyor France
Ireland orta noktada anlasiyor France
10.0
Belgium tarafina geciyor Netherlands
Luxembourg tarafina geciyor Netherlands
Ireland tarafina geciyor Netherlands
7.0
Yeni Model
BDM'in yeni modeli yeni parametreler kullanıyor, örnek mugabe-full.csv
içinde bulunabilir. Uzun yıllar başta kalan bir diktatör Mugabe'nin nasil o
noktada kalabildiğini destekcileri uzerinden görmek mümkün, bir türlü gitmek
bilmeyen liderlerin arkasındaki dinamikleri anlamak için bilgilendirici
herhalde!
Hocanın yeni modeli [4,9]'ta anlatılıyor fakat, kodlamak için hala yeterli bilgi
yok. Aslında eski kod için de yeterli bilgi yok, fakat [10]'daki araştırmacı
kolları siyayıp tüm makalelerde anlatılanları birleştirerek bir kod çıkartmaya
uğraşmış. Bir örneği masad/emissions.py içinde bulabiliriz.
Kaynaklar
[1] Stack Exchange, Expected Utility Method and a Repeated Game Solution, http://math.stackexchange.com/questions/1366279/expected-utility-method-and-a-repeated-game-solution
[2] Bueno De Mesquita BB (1994) {\em Political forecasting: an expected utility method}. In: Stockman F (ed.) European Community Decision Making. Yale, CT: Yale University Press, Chapter 4, 71-104.
[3] Scholz, Unravelling Bueno De Mesquita's group decision model, https://oficiodesociologo.files.wordpress.com/2012/03/scholz-et-all-unravelling-bueno-de-mesquita-s-group-decision-model.pdf
[4] A New Model for Predicting Policy Choices: Preliminary Tests http://irworkshop.sites.yale.edu/sites/default/files/BdM_A%20New%20Model%20for%20Predicting%20Policy%20ChoicesREvised.pdf
[5] Eftekhari, Preana: Game Theory Based Prediction with Reinforcement Learning, http://www.scirp.org/journal/PaperDownload.aspx?paperID=49058
[6] The Predictability of Foreign Policies, The British EMU Policy, https://www.rug.nl/research/portal/files/3198774/13854.pdf
[7] J. Velev, Python Code, https://github.com/jmckib/bdm-scholz-expected-utility-model.git
[8] The Visible Hand, http://s3.amazonaws.com/os_extranet_files_test/27236_59690_fa12visible.pdf
[9] Mesquita, The Predictioneer's Game
[10] Masad, Replicating the replication of BDM's Expected Utility Model, https://github.com/dmasad/BDM_DecisionModel_Replication
Yukarı