Log Lineer Modeller ve Koşulsal Rasgele Alanlar (Log Linear Models and Conditional Random Fields -CRF-)

Charles Elkan ders notları

Elkan'ın yapay öğrenim konusuna bakışı ilginç, ona göre yapay öğrenim bir bilgisayar bilim (computer science) konusudur, mesela altta işlenen maksimum olurluk bilgisayar bilimdir.

Koşulsal Olurluk (Conditional Likelihood)

Diyelim ki elimizde eğitim verisi olarak ikili $< x,y >$ veri noktaları var. O zaman $y$'nin $x$'e koşulsal olarak bağlı (conditional on) bir dağılımı olduğunu söyleyebiliriz.

$$ y \sim f(x;\theta) $$

Yani her $x$ için farklı bir $y$ dağılımı ortaya çıkabilir. Ve tüm bu farklı dağılımların ortak noktası $\theta$ parametresidir. Koşulsal olasılık yani şöyle yazılabilir,

$$ P(Y=y | X=x;\theta) $$

Üsttekiler $Y$ için bir model ortaya koydu, peki elimizde $X$'in dağılımı için bir olasılık modelimiz var mı? Cevap hayır. Niye? Düşünelim, $p(y,x)$ nedir ?

$$ p(x,y) = p(x)p(y|x) $$

Üstte $p(y|x)$'i tanımlayacak ($\theta$ üzerinden) bir olasılık demeti / ailesi tanımladık, fakat elimizde $p(x)$ dağılımını verecek bir model yok, o zaman $p(x,y)$'yi tanımlayacak bir model de yok.

Fakat bu dünyanın sonu değil. Belki de Yapay Öğrenim (machine learning) branşının bir sloganı şu olmalı: "Öğrenmen gerekmeyen şeyi öğrenme". Üstteki örnekte $p(y|x)$'i öğrenebiliriz, ama $p(x)$'i illa öğrenmemiz gerekir mi?

Sınıflayıcı (classifier) ve denetimli (supervised) öğrenim durumunu düşünürsek, bize eğitim amaçlı olarak $< x,y >$ ikili veri noktaları sağlanacak. $x$ kaynak veri, $y$ tahmin edilecek (ya da başta eğitim hedefi olan) etiket olacak. $y$ için bir model ortaya çıkartıyoruz, çünkü test zamanında $y$ olmayacak, fakat $x$ hep olacak. Yani $y$'nin modellenmesi mecburi, çünkü "genelleyerek" onun ne olduğunu bulacağız, ama $x$ hep verili.

Koşulsal Olurluk Maksimum Olurluk Prensibi

Eğitim verisi $< x_1,y_1 >,...,< x_n,y_n >$ için, $\theta$'yi şöyle seç

$$ \hat{\theta} = \arg\max_{\theta} \prod_{i=1}^{n} p(y_i | x_i;\theta) $$

Normal maksimum olurlukta bilindiği gibi olasılıkların çarpımı maksimize edilir, burada maksimize ettiğimiz "koşulsal" olasılıkların çarpımı.

Burada önemli bir soru şu: bildiğimiz gibi maksimum olurluk hesabı her veri noktasının bir diğerinden bağımsız olduğunu farzeder [çünkü her olurluk hesabını bir diğer ile çarpıyoruz, başka ek çarpım, toplama, vs yapmıyoruz], bu faraziye doğru bir faraziye midir? Bu soru ve ona verilecek cevap çok önemli. Evet, eğer eğitim noktaları birbirinden bağımsız değilse maksimum olurluk kullanmamalıyız. Bağımsızlığı da iyi tanımlamak gerekiyor tabii, eğer üstteki durumda $x_i$ verildikten sonra $y_i$'ların birbirinden bağımsız olması yeterli.

Bu model klasik İstatistik'te çokça kullanılan bir yaklaşımdır, hatta lineer regresyon'un temeli üstteki faraziyedir.

$$ y = \alpha + \bar{\beta}\bar{x} + N(0,\sigma^2) $$

Bu standart lineer regresyon modeli, ve bu modelde her $y$ ona tekabül eden $x$'e bağlı, bu sayede $x$'ler biliniyorsa $y$'ler birbirinden koşulsal olarak bağımsız hale geliyor, böylece $x$'ler birbirine bağımlı olsa bile $\alpha$ ve $\beta$'nin bulunması mümkün oluyor.

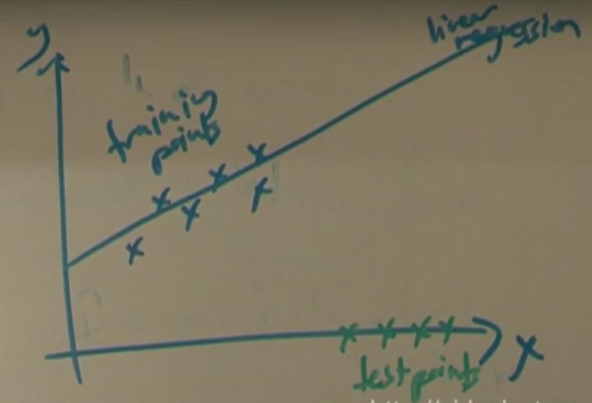
Üstteki resimde eğitim noktaları (training points) mavi olsun, test noktaları yeşil olsun (hemen altında). Bazı Yapay Öğrenim yaklaşımları diyebilir ki eğitim $x$'lerinin dağılımı test $x$'lerinin dağılımından farklı, bu veri seti öğrenilemez (yani genellenemez, modellenemez). Fakat klasik İstatistik buna bakar ve der ki $x$'lerin verildiği durumda $y$'ler bağımsızdır, bu şekilde bir koşulsal model öğrenilebilir.

Lojistik Regresyon aynı şekilde işler (lojistik regresyon, log lineer modellerin özel bir halidir, CRF'ler aynı şekilde). Burada da öğrenilen bir

$$ p = p(y | x;\alpha,\beta) $$

modeli vardır ve $y$ değerleri sadece 0 ve 1 olabilir. Tahmin edilen olasılık ise $y$'nin 1 olma olasılığıdır. Bu model Rasgele Gradyan Çıkışı ile eğitilir [detaylar için bkz Lojistik Regresyon notları].

$$ log \frac{p}{1-p} = \alpha + \sum_j \beta_j x_j $$

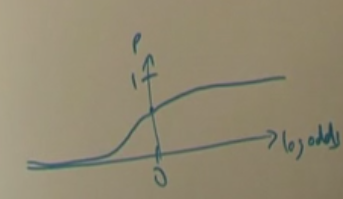
$p$ log şansının monotonik bir fonksiyonudur, ve ters yönden bakarsak, log şans $p$'nin monotonik bir fonksiyonudur. Yani lineer bir fonksiyon (sağ taraf) ne kadar büyürse, olasılık / log şans o kadar büyüyecektir. Bu büyüme durumu mesela $\beta_j$ katsayısını veri analizi bağlamında yorumlanabilir hale getirir. Diyelim ki $\beta_4$ katsayısı pozitif, o zaman diğer tüm şartların eşit olduğu durumda (with all else being equal) $x_4$ ne kadar buyurse 1 olma olasılığı o kadar artar.

Lojistik modellerin önemli bazı avantajları var, ki bu avantajlar log lineer modellere de sirayet ediyor (bu iyi).

1) Değişkenler arası ilinti (correlation) probleme yol açmaz: Bu fayda aslında daha önce belirttiğimiz $x$'lerin birbirine bağımlı olabilmesi ile alakalı. Bağımsızlık önşartı aranmadığı için istediğimiz kadar $x$'i problemin üzerine atabiliriz, eğitici algoritma bunlardan çıkartabildiği kadar iyi bir model bulacaktır.

Kıyasla mesela Naive Bayes böyle değildir, eğer bir NB sınıflayıcısını eğitiyorsak, ve öğelerin (feature) arasında ilinti var ise, sınıflayıcının doğrulugu (accuracy) azalabilir.

2) LR ile "1 olma olasılığını", yani "bir sayısal skoru", elde ediyoruz, bu sadece 1/0 değerinden daha fazla bir bilgi demektir.

3) Bu skor, anlamı olan bir olasılıksal değerdir: Sonuçta SVM sınıflayıcıları da $-\infty$ ve $+\infty$ arasında değerler döndürürler, ve bu değerler sıralama (ranking) amaçlı kullanılabilir, fakat olasılık matematiği açısından anlamı olan bir değerin olması bundan bile iyidir. Naive Bayes 0 ve 1 arasında değer döndürebilir, fakat bu değerlerin de olasılıksal olarak aslında anlamı yoktur, pratikte görüldü ki bu değerler çok uç noktalarda, ya sıfıra çok yakın, ya bire çok yakın. Literatürde NB skorlarının "iyi kalibre edilmiş olmadığı" söylenir.

$X_1,...,X_n$ test örnekleri ve tahmin edilen olasılıklar $P(Y=1 | x_i) = v_i$ olsun. Diyelim ki $s = \sum_i v_i$ ve $t$ sayısı $1,..,n$ tane öğenin içinden $y = 1$ değerini taşıyan öğelerin sayısı olsun. Örnek, elimizde 100 tane eğitim noktası var, bunların 60'ı 1 değerinde. Bu durumda $s$ yaklaşık 60 olacaktır (rasgele gürültüyü hesaba katarsak tabii), yani $E[t] = s$ denebilecektir ve bu sadece eğer olasılıklar iyi kalibre edilmişse söylenebilir.

4) Dengesiz eğitim verisi kullanılabilir: pek çok eğitim setinde mesela 1 değeri taşıyan değerleri 0 değeri taşıyanlardan çok daha fazla. Lojistik regresyon bu tür veriyle rahatça çalışabilir.

Ders 3

Lojistik regresyon için log olurluğun (LCL) türevini almak lazım. Önce basitleştirme amaçlı $\alpha = \beta_o$, ve $x_0 = 1$. O zaman log şansın eski hali (altta eşitliğin sol tarafı) şöyle yazılabilir (sağ taraf), daha derli toplu bir formül olur,

$$ \alpha + \sum_j \beta_j x_j = \sum_{j=0}^{d} \beta_j x_j $$

Bulmak istediğim her $j$ için $\frac{d}{d\beta_j} LCL$ lazım

$$ \frac{d}{d\beta_j} LCL = \sum_{i:y_i=1} \frac{d}{d\beta_j} \log p(1|..) + \sum_{i:y_i=0} \frac{d}{d\beta_j} \log p(0|..) \qquad (3) $$

Eğer üstteki bir bölümü $p$ diğerine $1-p$ dersem, yani şöyle

$$ = \sum_{i:y_i=1} \frac{d}{d\beta_j} \underbrace{\log p(1|..)}_{p} + \sum_{i:y_i=0} \frac{d}{d\beta_j} \underbrace{\log p(0|..)}_{1-p} $$

O zaman

$$ = \sum_{i:y_i=1} \frac{d}{d\beta_j}\log p + \sum_{i:y_i=0} \frac{d}{d\beta_j} \log (1-p) $$

Biliyoruz ki

$$ \frac{d}{d\beta_j}\log p = \frac{1}{p}\frac{d}{d\beta_j} p \qquad (1) $$

$$ \frac{d}{d\beta_j}\log (1-p) = \frac{1}{1-p}(-1)\frac{d}{d\beta_j} p \qquad (2) $$

Üstteki son iki formülün her ikisinde de $d/d\beta_j p$ kısmı olduğuna dikkat.

Notasyon

$$ e = \exp \big[ - \sum_{j=0}^n \beta_jx_j \big] $$

$$ p = \frac{ 1}{1+e} $$

$$ 1-p = \frac{ 1+e-1}{1+e} = \frac{ e}{1+e} $$

Şimdi $d/d\beta_j p$'e dönelim, ve $p$'nin üstteki gibi olduğundan hareketle,

$$ \frac{ d}{d\beta_j}p = (-1)(1+e)^{-2} \frac{ d}{d\beta_j}e $$

$$ = (-1)(1+e)^{-2} (e) \frac{ d}{d\beta_j}(x_j) $$

$$ = \frac{ 1}{1+e} \frac{ e}{1+e}x_j = p(1-p)x_j$$

Son ifade kodlama için oldukça uygun, $d/d\beta_j p$ hesabını yine içinde $p$ içeren bir ifadeye bağladık, ayrıca türev $x_j$ ile orantılı.

Bu hesapla aslında (1) içindeki $d/d\beta_j p$ kısmını hesaplamış olduk. Eğer yerine koyarsak,

$$ \frac{d}{d\beta_j}\log p = \frac{1}{p}p(1-p)x_j $$

$p$'ler iptal olur

$$ = (1-p)x_j $$

Aynı şekilde (2) için

$$ \frac{d}{d\beta_j}\log (1-p) = \frac{1}{1-p}(-1) p(1-p)x_j $$

$$ = -px_j $$

Üstteki türevler tek bir eğitim veri noktası için. Tüm eğitim veri setinin türevi her noktanın türevlerinin toplamı olacak, (3)'de görüldüğü gibi.

$$ \frac{d}{d\beta_j} LCL = \sum_{i: y_i = 1} (1-p_i)x_{ij} + \sum_{i: y_i = 0} -p_i x_{ij}
\qquad (4) $$

$x_{ij}$ notasyonunda $j$, $j$'inci öğe / özellik anlamına geliyor. Şimdi notasyonel bir numara kullanacağım,

$$ = \sum_{tum \ i} (y_i - p_i)x_{ij} $$

Bunu niye yaptım? (4) formülünde eşitliğin sağ tarafı, birinci terim içinde 1 sayısı var, sonraki terimde 1 yok. Eğer 1 olup olmaması yerine $y_i$ kullanırsam, ki zaten 1'in olup olmaması $y_i$'nin 1 olup olmamasına bağlı, tek bir terimde işi halledebilirim. $y_i=1$ olduğu zaman üstteki ifade $1-p_i$ olacaktır, olmadığı zaman $-p_i$ olacaktır.

Eriştiğimiz sonucu analiz etmemiz gerekirse, nihai formül gayet basit ve temiz çıktı.

[24:10] kalibrasyonla alakalı bir yorum

Rasgele Gradyan Çıkışı (Stochastic Gradient Ascent)

Fikir: türevi eğitim noktası basına hesapla, ve modeli hemen güncelle.

Eğitim noktaları $< x,y >$ olarak gelsinler. Her nokta için, ve her $\beta_j$ için

$$ \frac{d}{d\beta_j}p(y|x;\beta) = g_j$$ hesapla.

$$ \beta_j := \beta_j + \alpha g_j $$

Gradyanın ne olduğunu hatırlayalım, bir fonksiyonun maksimumuna "doğru" olan bir gidiş yönünü gösterir, ve bu gidiş yönü o fonksiyonu oluşturan değişkenlerin (parçalı türevleri) üzerinden belirtilir. O zaman elimizdeki gradyan o iç değişkenlerin maksimum yöndeki değişim şeklini bize tarif eder.

Algoritmanın tamamı: alttaki formül için

$$ \frac{d}{d\beta_j}p(y|\bar{x};\bar{\beta}) = (y-p)x_j $$

Her $x$ için

• O anki modele göre $p$'yi hesapla

• Her $j = 0,..,d$ için

\ \ \ - $ \beta_j := \beta_j + \alpha \underbrace{ (y-p) x_j}_{\textrm{kısmi türev}} $ hesapla

Peki metotun ismindeki "rasgele (stochastic)" tanımı nereden geliyor? İyi bir soru bu çünkü metotta rasgele sayı üretimi gibi şeyler görmüyoruz. Cevap, metot yine de rasgele, çünkü her noktayı ayrı ayrı işliyoruz, ve bu noktaların eğitim algoritmasını gelişi bir nevi "veriyi örneklemek" gibi sanki, ek olarak veriyi eğitime almadan önce rasgele şekilde karıştırmak ta iyi olabilir.

Bazı Tavsiyeler (Heuristics)

1) Her özellik (feature) $x_j$'i ölçeklemek, yani aynı ortalama (mean) ve varyansa sahip olacak şekilde tekrar ayarlamak. Yani mesela 0 ile 100 arasında olabilecek "yaş" gibi bir özelliği, 0 ve 1 arasında değişen özellikler ile aynı ortalama ve varyansa sahip olacak şekilde ayarlamak. Bunun sebebi güncelleme hesabındaki $\lambda$'nin tek bir sabit olması, ve bu sabit her $j$ için aynıdır, o sebeple $\lambda$'nin her öğeye "aynı şekilde" uygulanabilmesi için öğelerin birbirine yakın olması iyidir. Ek olarak, genellikle eğitim verisinde 0 ile 1 arasında ikisel türden öğeler vardır, o sebeple bu şekilde olmayan diğer ögeleri 0 ve 1 arasında çekmek daha uygun ve kolay olur.

2) Veriyi rasgele şekilde sıralamak. Terminoloji: eğitim veri seti üzerinden bir geçiş yapmak bir "çağ" (epoch) olarak bilinir.

3) $\lambda$'yi deneme / yanılma yöntemi ile bulun (bu sabiti bulmanın sistemik bir yöntemi yok). Belki verinin içinden alınan daha ufak bir örneklem üzerinde bu deneme / yanılma işlemi yapılabilir.

4) Deneme yanılma işlemini şöyle yapabilirsiniz: büyük bir $\lambda$ ile ise başlarsınız, ve her çağda $\lambda$ değerini azaltabilirsiniz (mesela her çağ sonunda $1/2$ ile çarparak).

Ders 4

Log Lineer Modeller

Bu modeller lojistik regresyonun yapıya sahip (structured) girdiler ve çıktılar için genellenmiş halidir. Lojistik regresyonda girdi $\bar{x} \in \mathbb{R}^d$ ve çıktı $y \in {0,1}$ idi, yani çıktı ikiseldi. Fakat biz bundan daha genel yapay öğrenim problemlerini çözmek istiyoruz, yani istediğimiz $x \in \mathbb{X}$, ki $\mathbb{X}$ herhangi bir uzay olabilmeli, ve $y \in \mathbb{Y}$ ki $\mathbb{Y}$ aynı şekilde herhangi bir uzay olabilmeli.

Mesela $x$ bir cümle olabilmeli, diyelim ki $x$ = "he sat on the mat", tercümesi "adam paspasın üzerinde oturdu". Buna karşılık olan $y$ ise mesela şöyle olabilmeli, $y$ = "pronoun verb article noun", yani her kelimenin hangi gramer ögesi olduğunu gösteren bir ibare. Mesela "sat" yani oturmak, bir fiil (verb), "mat" paspas, bir isim (noun), ve $y$ içinde gelen eğitim verisinde bunlar olabilmeli (üstteki örnekte ikinci öğe), sadece 0/1 değerleri değil.

Bu tabii ki denetimli bir eğitim şekli olacak. Fakat dikkat bazı yapay öğrenim uygulamalarında "çok sınıftan gelen" ama tek bir değer vardır, mesela $y \in {1,2,3}$ olabilir, 3 sınıflı bir çıktı yani. Bazen çıktı gerçek sayı (real number) olabilir, ama yine de tek bir $y$ değeri vardır. Üstteki durum böyle değildir. Potansiyel olarak $y$'nin büyüklüğü $x$ ile birebir aynı bile olmayabilir. Bu tür bir karışık eşlemeden bahsediyoruz. Tek sınırlamamız $\mathbb{Y}$'nin sonlu (finite) olması.

Model şöyle (notasyonu biraz değiştirdik, $\beta$ yerine $w$ kullanıyoruz mesela, $w$ modelin "ağırlıklarını (weights)" temsil ediyor.

$$ p(y|x;w) = \frac{\exp \big[ \sum_{j} w_j F_j (x,y) \big]}{Z(x,w)} $$

Yakından bakarsak model LR modeline benziyor. Bir lineer fonksiyonun $\exp$'sı alınıyor ve bu değer olasılık hesabında kullanılıyor. İleride zaten göreceğiz ki LR üstteki yaklaşımın bir "özel durumu", yani üstteki model daha genel bir tanım.

Aklımıza birçok soru geliyor herhalde, mesela "$Z$ nedir?" ya da "$F_j$ nasıl hesaplanır?" gibi. $Z$ şöyle tanımlanır

$$ Z(x,w) = \sum_{y'} \exp \big[ \sum_j w_j F_j(x,y') \big] $$

Tüm $y'$'lere bakılıyor, yani tüm mümkün $\mathbb{Y}$ değerleri teker teker $y'$ üzerinden toplamda kullanılıyor. $\mathbb{Y}$'nin sonlu olma faraziyesi burada önemli hale geliyor, toplamı sonsuz bir küme üzerinden yapamayız.

$Z$ normalizasyon için kullanılıyor, çünkü olasılık teorisinde eğer elimizde çoklu bir hedef var ise, bu hedeflere olan olasılık değerlerinin toplamı 1 olmalıdır. $Z$ işte bunu garantiler, bu sebeple bölen (denominator) bölümün (nominator) toplamı olmalıdır.

Her $F_j(x,y)$ bir özellik fonksiyonudur (feature function). Niye? Çünkü elimdeki $x$'ler illa bir vektör olmayabilir, yani $x_j$ "vektörünü" alıp $w_j$ "vektörü" ile çarpamam, bu sebeple önce bir fonksiyon ile bir sayısal (numerical) değer üretmem gerekiyor. Küme olarak

$$ F_J: \mathbb{X} \times \mathbb{Y} \to \mathbb{R} $$

Eğer $ F_j(x,y) > 0 $ ve $w_i > 0$ ise, o zaman $F_j(x,y) = 0$'a kıyasla $p(y|x;w)$ artar. Sezgisel olarak tarif edersek özellik fonksiyonun (OF) söylediği şudur, eğer ağırlık pozitif ise OF'in değeri ne kadar buyurse elimizdeki $y$, $x$ ile o kadar "uyumludur" (tabii ki belli bir özellik yani $j$ için). Negatif ilinti bunun tam tersi olurdu.

Eğitim $w_j$ ağırlıklarını bulmamızı sağlar. $F$ önceden tanımlıdır (yani eğitime bile başlamadan önce), bu fonksiyonun ne olacağı "seçilir". Seçilirken tabii ki $x,y$ arasındaki ilintiye göre fazla / az sonuç geri getirebilecek şekilde seçilmelidir.

Kelime örneğine geri dönersek, bir $F$ şöyle olabilir,

$ F_{15}(x,y) =$ "eğer ikinci kelimenin baş harfi büyük ve ikinci etiket isim (noun)". OF'ler reel değerlidir. Bunun özel durumu 0/1 değeri veren OF'lerdir. Biraz önceki örnek mesela 0/1 döndürüyor.

Ya da $F_{14}(x,y)$ diyelim ki şöyle "ilk kelimenin baş harfi büyük, ve ilk etiket bir isim". Tahmin edebiliriz ki eğitim setimizde ilk kelimesinin baş harfi büyük olan ama o kelimesi isim olmayan pek çok örnek olacaktır. Bu durumda $w_{14}$ küçük olur.

Dediğimiz gibi $F$ reel değeri olabilir, mesela

$$ F_{16}(x,y) = length(y) - length(x) $$

yani bu fonksiyonda $x$'nin uzunluğunu $y$'nin uzunluğundan çıkartıyoruz. Bu ne işe yarar? Diyelim ki otomatik tercüme yapması için bir yapay öğrenim programı yazıyoruz, $x,y$ eğitim noktaları birbirinin tercümesi olan İngilizce/Fransızca cümleler. Çoğunlukla Fransızca cümleler tekabül ettikleri İngilizce cümlelerden çok daha uzun oluyorlar, yani üstteki çıkarma çoğunlukla pozitif sonuç verecek. Değişik bir açıdan bakarsak, pozitif bir sonuç, bir tercümenin doğru olduğu yönünde bir işaret olarak kabul edilebilir, ve üstteki OF üzerinden eğitim algoritması bunu kullanır. Eğitim sonrası $w_{16}$ pozitif bir ağırlık alacaktır.

Bir log lineer modelde (buna CRF'ler de dahil) ilk yapılan iş probleminiz için önemli olan OF'leri ortaya çıkartmak.

$F$ tanımlamanın değişik bir başka yolu:

$a(x)$ bir fonksiyon olsun. Her $v \in \mathbb{Y}$ için

$$ F_j(x,y) = a(x) I(y=v)$$

tanımlayalım.

$$ p(y|x;w) = \frac{\exp \sum_j w_j F_j (x,y)}{Z} $$

Şimdi lineer zincirli CRF konusuna bakalım. Yine $x \in \mathbb{X}$ ve $y \in \mathbb{Y}$. $x$ bir girdi zinciri, $y$ bir çıktı zinciri ve en basit durumda $x$ ile aynı uzunlukta. Konuşma bölümlerini etiketlemek bu kategoriye dahil, ama bir diğer uygulama kelimeyi arasına eksi işaretleri koyarak bölme (hyphenation).

Mesela girdi $x=$"beloved", çıktı $y=$"00100000" çünkü bu kelime "be-loved" olarak bölünür.

Bu uygulama için bir OF

$$ F_j(x,y) = \frac{\textrm{kaç tane 1 var}}{\textrm{x uzunluğu}} $$

$x=$"beloved", çıktı $y=$"00100000" için sonuç $1/7$ olurdu.

Lineer zincir CRF için hangi OF'lerin bazı sınırları var.

$$ F_j (\bar{x},\bar{y}) = \sum_i f_j(y_{i-1}y_i\bar{x} i) $$

ki sembol üzeri düz çizgiyi ($\bar{x}$ gibi) bu sefer bir sıralı veri temsil etmek için kullanıyorum)

Mesela

$$ f_{18} = f_j(y_{i-1}y_i\bar{x} i) = " i=2, y_{i-1} = 0, y_i = 1, x_1x_2 = "as" "$$

Mesela "async" kelimesi "a-sync" olarak bölünebilir, ve eğitim setinde "async" ile "$y=$01..." gelirse üstteki OF bu bölünmeyi ödüllendirir / öğrenir.

Şimdi CRF olmayan bir Lineer Model'e bakalım,

Mesela çok etiketli denetimli (supervised) öğrenim. "Çok etiketli" ne demektir? Dikkat, "çok sınıflı (multi label)" değil, yani tek öğenin iki veya daha fazla değer arasından birini seçmesinden bahsetmiyoruz. Birden fazla etiket alabilmekten bahsediyoruz, mesela bir İnternet sayfası, bir veya daha fazla kategoriye aynı anda ait olabilir, mesela hem Spor, hem İş Dünyası. Diyelim ki 10 mümkün etiket var, bir doküman kaç değişik şekilde etiketlenebilir?

$2^{10} = 1024$ şekilde (bu sayı, hesap bir kümenin kaç değişik şekilde alt kümesi olabilir hesabını yansıtıyor aynı zamanda, yani sıralama önemli olmadan belli sayıda öğenin kaç değişik şekilde alt kümeleri olabilir sorusu). Bu büyük bir rakam. Ve bu kadar çok olasılık var ise, eğitim verisi tüm kombinasyonlar için örnek veri içermeyebilir. Fakat muhakkak algoritmamızın bu kombinasyonları tahmin edebilmesini tercih ederiz.

Çözüm? 10 değişik sınıflayıcı kurarark bu problemi çözebiliriz (ayrı ayrı, tek başına tek sınıfa bakılınca yeterli veri çıkar herhalde), fakat bu şekilde "sınıflararası" ilişkileri yakalayamayız. Log lineer model yaklaşımında öyle bir ikisel (binary) OF yaratırsınız ki, mesela,

$$F_{19}(x,y) = "Spor \in y, \textrm{İş Dünyası} \in y" $$

Dikkat edersek OF sadece $y$'ye bakıyor. Bu OF'yi içeren algoritma eğitilince üstteki OF için bir pozitif ağırlık öğrenilebilecektir.

Soru: bir anlamda problemin yerini değiştirmiş olmuyor muyuz? Mesela üstteki şekilde bu sefer her türlü kombinasyon için OF'mi yaratacağız? Cevap: eğer sadece ikili eşlere bakıyorsak, kombinasyon hesabı $C(10,2) = 45$ sonucunu verir. Bu fena bir sayı değil.

Ayrıca verinin seyrekliği bize hangi kombinasyonların dahil edilip edilmeyeceği yönünde yardımcı olabilir.

Soru: çok sınıflı problemler lojistik regresyonu geliştirerek çözülemez mi? Cevap: böyle bir yaklaşım var, buna multinom lojistik regresyon deniyor. Fakat bu yaklaşımın log lineer modellerin özel bir hali olduğunu belirtmek isterim, yani yapay öğrenim dünyasının aktif olarak araştırdığı alan artık burası, multinom lojistik regresyon aşıldı. Zaten log lineer modeller ile çok etiketli problemleri de çözebiliyorsunuz.

Ders 5

Soru: biraz önce sadece $y$'ler arasında bir OF tanımlayabildiğimizi gördük. Peki sadece $x$'ler arasında OF tanımlamak faydalı olur muydu? Cevap: Formülü tekrar hatırlayalım,

$$ p(y|x;w) = \frac{\exp \sum_j w_j F_j (x,y)}{Z(x,w)} $$

OF'nin görevi hangi $y$'lerin daha yüksek olasılığı olduğunu belirtmek. Eğer sadece $x$ var ise, bu durumda bölüm ve bölendeki değerler birbirini iptal ederdi. Her $y$ için aynı $x$ "katkısı" olurdu ve bunun sınıflayıcıya hiçbir faydası olmazdı.

[8:00-18:00 atlandı]

Çözdüğümüz problemler şu formatta

$$ p(\bar{y}|\bar{x};w) = \frac{\exp \sum_j w_j F_j (\bar{x},y)}{Z(\bar{x},w)} $$

Tahmin etmek için

$$ \hat{y} = \arg\max_{y} \exp \sum_j w_j F_j(\bar{x},y)$$ Bir $\bar{y}$ tahmin etmek için bu modellerden birini kullanacaksak, $ p(\bar{y}|\bar{x};w)$ formülüne $\bar{x}$'i koyarız, ve elde edilen dağılımda hangi $\bar{y}$'nin olasılığı daha yüksekse onu seçeriz. Daha yüksek olasılığa sahip olan $\bar{y}$, $p(\bar{y}|\bar{x};w)$ formülünde bölümü daha yüksek olandır. Bölen her $\bar{y}$ için sabit / aynı.

Aslında $\exp$'ye ihtiyaç yok, çünkü $\exp$ monotonik bir fonksiyon, yani sadece şu kullanılabilir,

$$ \hat{y} = \arg\max_{y} \sum_j w_j F_j(\bar{x},y)$$

En olası $y$'yi bulmak için $Z$'nin gerekmediğine de dikkat, çünkü bu sabit tüm seçenekler için aynı.

Burada tahmin etmek bağlamında zor olan şey, en yüksek $y$'yi bulmak için tüm $y$'lere teker teker bakmaya mecbur olmamız. Bu bakma işlemi çok zaman alabilir, o zaman bu problemi bir şekilde çözmem lazım.

Diğer problem, tüm olasılıkların 1'e toplanabilmesini sağlayan normalize sabitinin hesabı, yani $Z(\bar{x},w) = \sum_{y'}\exp [ \sum_j w_j F_j(\bar{x},\bar{y})]$, ki eğer olasılık değeri hesaplayacaksak bu sabit gerekli.

Yani iki ana problem var, bir de eğitim algoritması var, ki bu aynen lojistik regresyon örneğinde olduğu gibi rasgele gradyan çıkışı üzerinden olacak, bu 3 algoritmayı şimdi sunacağız.

Algoritma 1

Önce,

$$ \hat{y} = \arg\max_{\bar{y}} \sum_j w_j F_j(\bar{x},\bar{y})$$

Bu hesabı polinom zamanda (polynomial time) yapmak istiyoruz. Tanımı biraz değiştirelim,

$$ = \arg\max_{\bar{y}} \sum_j w_j \sum_i f_j(y_{i-1}y_i \bar{x} i )$$ $j$ tüm özellikler, $i$ $x,y$ "boyunca" ilerleyen indisler. Üstteki ibare tek bir eğitim veri noktası için yapılıyor, yani $i$ değişik veri noktalarını indislemiyor (genellikle öyle olur, o yüzden belirtmek istedik).

Toplam işlemlerinin sırasını değiştirelim,

$$ = \arg\max_{\bar{y}} \sum_i \sum_j w_j f_j(y_{i-1}y_i \bar{x} i )$$ İçerideki toplama $g_i(y_{i-1}y_i)$ ismi verelim, böylece her $i$ için değişik bir $g$ fonksiyonuna sahip oluyorum.

$$ = \arg\max_{\bar{y}} \sum_i g_i(y_{i-1}y_i) $$

$y_{i-1},y_i$ kelime bölme probleminde iki değerden birini alabilir. Cümle etiketleme probleminde belki 20 değerden birini alabilirler. $\bar{x},\bar{w}$ zaten sabit (eğitim verisi içindeler, ya da sabit olarak görülüyorlar). Bu durumda $g$'yi temsil etmek için nasıl bir veri yapısı kullanmalıyım? Çünkü bilgisayar bilim yapıyoruz, ve bilgisayar bilimde veri yapıları vardır. Bize gereken belli $y_{i-1},y_i$ kombinasyonu için bir $g$ değeri döndürülmesi, ve bu sonucu bir yerde depolayabilmek.

Gereken yapı basit bir matris olabilir. Diyelim ki $m$ farklı $y$ değeri var ise, $m^2$ hücresi olan bir matris işimizi görür. Her $g_i$ için ayrı bir $m^2$ matrisi olacak tabii ki. $n$ tane matris, $d$ değer var ise işlem zamanı $O(m^2nd)$.

Algoritmamda ilk yapacağım iş mümkün $g$ değerlerini önceden hesaplayıp (precompute) bir yerde depolu olarak tutmak / hazır etmek.

Tanım

$Skor(y_1,...,y_k) = \sum_{i=1}^{k} g_i(y_{i-1} y_i)$

Amacımız öyle bir $y$ sıralaması (sequence) bulmak ki bu sıranın skoru en yüksek olsun.

$U(k)$ = en iyi sıralama $y_1,...,y_k$'nin skoru

$U(k,v)$ = $y_k=v$ olma şartıyla en iyi sıralama $y_1,...,y_k$'nin skoru

Amacım $U(n+1, \textrm{BİTİŞ})$'i bulmak. Mümkün etiketlere BAŞLA, BİTİŞ adlı iki yeni değer ekledik, bu bazı formülleri kolaşlaştıracak. Bu tanım aslında $\arg\max$ ile bulmaya çalıştığım şeyin bir bölümj aslında, sadece amacımı bu şekilde tekrar tanımladım. Tekrar belirtmek gerekirse,

$$U(k,v) = \max_{y_1,y_{k-1}} [ \sum_{ i=1}^{k-1} g_i(y_{i-1}y_i) + g_k(y_k,v) ]$$

İlginç bölüme geldik. Üstteki tanımı özyineli olarak tanımlarsak,

$$ U(k,v) = \max_{y_{k-1}} [ U({k-1},y_{k-1}) + g_k(y_{k-1},v)] $$

Bu özyineli fonksiyonun avantajı nedir? Aslında bir önceki formüle göre çok daha çetrefil duruyor. Avantaj şurada, dinamik programlama (dynamiç programming) tekniklerini kullanarak bir döngü içinde üstteki özyineli hesabı yapmak mümkün. Şimdi teker teker bakalım,

$y_0 = \textrm{BAŞLA}$

$U(1,v) = \max_{y_0} [ U(0,y_o) + g_1(y_0,v)]$

Bu ilk basamakta aslında bir maksimizasyon yok, o zaman

$ = g(\textrm{BAŞLA},v)$

yeterli.

Ama ikinci basamakta işler zorlaşıyor,

$U(2,v) = \max_{y_1} [ U(1,y_1) + g_2(y_1,v) ]$

Fakat eşitliğin sağ tarafındaki $U$ hesabını bir önceki basamakta hesapladım ve depoladım, onu hemen kullanabilirim. Bu hesabın yükü nedir? Her mümkün $v$ değerine ($m$ tane) bakmam lazım, ve bu işlem sırasında her $y_1$ mümkün değeri (yine $m$ tane) irdelemem lazım. Yani $O(m^2)$.

Bu işlemi $U(n+1, \textrm{BİTİŞ})$'e kadar yapmam lazım. Toplam yük $O(nm^2)$.

$g$ matrislerini hesaplamak için $O(nm^2d)$ demiştik, bu $O(nm^2)$'ten daha büyüktür / ona baskındır, ve $O$ aritmetiğine göre daha büyük olan kullanılır.

Bu algoritma dinamik programlamanın özel bir halidir, bazen ona Viterbi algoritması ismi de verilir. Bilindiği gibi Viterbi algoritması Gizli Markov Modelleri (Hidden Markov Models) yapısını dekode etmek için kullanılıyor. CRF'lerin HMM'e kısmen bağlantısı olduğu düşünülürse, Viterbi algoritmasının burada da ortaya çıkması şaşırtıcı değil.

Algoritma 2

Şunu hesapla

$$Z(\bar{x},w) = \sum_{y'} \exp \underbrace{\sum_j w_j F_j(\bar{x},\bar{y})}_{g} $$

İçerideki toplama $g_i$ demiştik,

$$ g = \sum_i g_i(y_{i-1}y_i) $$ Yani

$$ Z(\bar{x},w) = \sum_{\bar{y}} \exp \sum_i g_i(y_{i-1}y_i) $$

Bir toplamın $\exp$'sı, $\exp$'lerin çarpımı haline dönüşür, yani $\exp$ toplamdan "içeri" nüfuz eder,

$$ = \sum_{\bar{y}} \prod_i \exp g_i(y_{i-1}y_i) \qquad (5) $$

$t=1,..,n+1$ için şunu tanımlayalım,

$M_t(u,v) = \exp g_t(u,v)$

$M_t$ aşağı yukarı $g$ ile aynı şey, her değişik $g$ fonsiyonu için değişik bir matris var, bu matris hücrelerinin $\exp$'sinin alınmış hali $M_t$ matrisi.

$M_1(u,v)$ sadece $u=\textrm{BAŞLA}$ için geçerli.

$M_{n+1}(u,v)$ sadece $b=\textrm{BİTİŞ}$ için geçerli.

$M_{12} = M_1M_2$ yani matris çarpımı.

$M_{12}(\textrm{BAŞLA},w)$'yu düşünelim (ki bu tek bir hücre değeri)

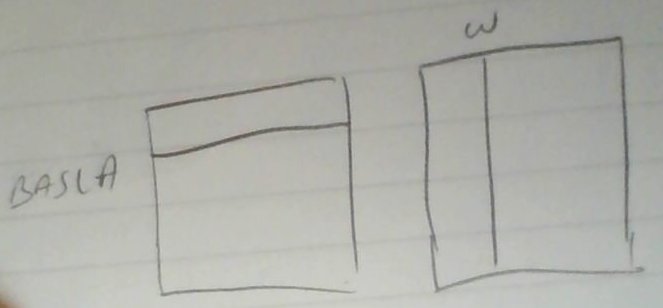
Bu ifadenin sol taraftaki $M_1$ içinde $\textrm{BAŞLA}$ satırını sağ taraftaki $M_2$ $w$ kolonu ile çarptığını düşünebiliriz.

$$M_{12}(\textrm{BAŞLA},w) = \sum_v M_1(\textrm{BAŞLA}, v)M_2(v,w) $$

$$ = \sum_v \exp [g_1(\textrm{BAŞLA},v) + g_2(v,w)] $$

Bu istediğimiz gibi bir ifadeye dönüşmeye başladı, çünkü hatırlarsak, (5)'e benzeyen bir şeyleri elde etmeye uğraşıyoruz. Gerçi üstteki ifade tüm $y$ değerleri için değil, tek bir $v$ için, ama yine de uygun, üstteki $v$ yerine $y_1$ dersek belki daha uygun olur,

$$ = \sum_{y_1} \exp [g_1(\textrm{BAŞLA},y_1) + g_2(y_1,w)] $$

Üçlü bir çarpma görelim: $M_{123}$.

$$ M_{123} = \sum_{y_2} M_{12}(\textrm{BAŞLA}, y_2)M_3(y_2,w) $$

$$ = \sum_{y_2} [ \sum_{y_1}\exp [g_1(\textrm{BAŞLA},y_1) + g_2(y_1y_2) ] \exp g_3(y_2,w) ] $$

$$ \sum_{y_1,y_2} \exp [g_1(\textrm{BAŞLA},y_1) + g_2(y_1y_2) + g_3(y_2,v)] $$

Yani üç matrisi birbiriyle çarparak $y_1,y_2$ üzerinden toplam almış oluyorum. Ve böyle devam edersem, yani tüm matrisleri birbiriyle çarparsam ve $\textrm{BAŞLA}, \textrm{BİTİŞ}$ değerlerine bakarsam,

$$ M_{123...n+1} (\textrm{BAŞLA}, \textrm{BİTİŞ}) =
$$ $$ \sum_{y_1,...,y_n} \exp [ (g_1(\textrm{BAŞLA},y_1) + g_2(y_1,y_2) + g_3(y_2,y_3) + ... + g_{n+1} (y_n, \textrm{BİTİŞ} ) ] $$

Bu ifade parçalara ayırma (partition) fonsiyonu için tam ihtiyacım olan şey. Daha önce Viterbi algoritmasından bahsettik, hatta bu algoritma dinamik programlama kategorisine girer dedik, üstteki algoritma dinamik programlama bile sayılmaz, aslında bir matris çarpımı sadece. Daha genel olarak üstteki algoritma ileri-geri (forward-backward) algoritmasının bir türevi, bu algoritmalar bildiğimiz gibi HMM'lerde sıkça kullanılıyorlar.

Bu iki algoritma CRF'ler için gerekli. Şimdi CRF'leri nasıl eğiteceğimizi görelim.

Eğitim

Maksimizasyon için rasgele gradyan çıkışı kullanacağız.

$$ p(y|x;w) = \frac{\exp \sum_j w_j F_j(x,y) }{Z(x;w)} $$

Gradyan çıkışı için üstteki formülün türevini alabilmeliyiz. Önce $\log$'unu almak lazım, çünkü $\partial / \partial w_j \log p$ hesabı gerekli, üsttekinin $\log$'u ise bölümün $\log$'u eksi bölenin $\log$'u.

$$ \frac{\partial}{\partial w_j} \log p = \frac{\partial}{\partial w_j} [ \sum_j w_j F_j(x,y)] - \frac{\partial}{\partial w_j} \log Z(x;w) $$

Türevin eksi öncesi ilk bölümü çok basit, $w_j$ ve toplam yokolacak (tüm $j$'lerin toplamı yokoldu, çünkü türev "tek" bir $j$ değeri ile ilgileniyor, diğerleri sıfır oluyor)

$$ = F_j(x,y) - \frac{\partial}{\partial w_j} \log Z(x;w) $$

Eksiden sonraki kısım çok zarif bir sonuca dönüşecek, birazdan göreceğiz.

$$ \frac{\partial}{\partial w_j} \log Z(x;w) = \frac{1}{Z} \frac{\partial}{\partial w_j} Z $$

Türevi toplam içine taşıyoruz,

$$ = \frac{1}{Z} \sum_{y'} \frac{\partial}{\partial w_j} [ \exp [ \sum_{j'} w_j' F_{j'}(x,y') ] ] $$

$$
= \frac{1}{Z}\sum_{y'} \bigg[ \exp [ \sum_{j'} w_{j'} F_{j'}(x,y') ] F_j(x,y') \bigg] $$

$$ = \sum_{y'} F_j (x,y') \frac{ \exp [ \sum_{j'} w_{j'} F_{j'}(x,y') ] } {Z} $$

Şimdi ilginç kısma geldik, üstteki kesirli kısım $p(y' | x;w)$ değerine eşittir.

$$ = \sum_{y'} F_j (x,y') p(y' | x;w)$$

İlginç durum burada ortaya çıkıyor, çünkü üstteki aynı zamanda bir beklenti (expectation) tanımı değil mi? Tüm $F_j$ değerlerini o değerlerin olasılıkları ile çarpıp toplarsak bir beklenti elde etmez miyiz? Evet. O zaman beklenti tanımını kullanabiliriz,

$$\frac{\partial}{\partial w_j} \log p = F_j(x,y) - E[F_j(x,y') ] $$

ki $y'$ şöyle bir dağılımı takip ediyor,

$$ y' \sim p(y'|x;w) $$

Soru: $\frac{\partial}{\partial w_j} \log p = ?$ Yani bu türev ne zaman sıfıra eşittir?

Cevap: Türevin açılımına bakınca mesela, $F_j=0$ olunca mı? Hayır, çünkü OF sıfır olsa bile beklenti kısmı sıfır olmayabilir. O zaman şöyle söylemek gerekir, eğer tüm $y'$ için $F_j(x,y') - 0$ ise, o zaman türev sıfır olur.

Çoğunlukla $F_j(x,y) = a(x)I(y=v)$. Hatırlarsak bu yöntem bir özelliği (ki $(a(x)$ ile temsil ediliyor), her mümkün $v$ değeri için bir OF'ye çevirmenin yolu idi (tek $x$'e bağlı OF olamaz).

O zaman şunu da söyleyebiliriz, eğer $a(x) = 0$ ise, her $y$ için $F_j(x,y) = 0$ demektir.

Bu bilginin faydası şudur, veride seyreklik var ise, lojistik regresyon bunları atlamayı bilir. Demek ki aynı şekilde koşulsal lineer modeller de bu özellikleri atlayabilir. Eğer bir özellik $a(x)=0$ ise, o özellik ağırlık güncellemesi (weight update) sırasında atlanır.

Algoritma train_crf

• Her eğitim noktası $x,y$ için

  • $j$ için

  • $E[F_j(x,y')]$ hesapla (buna sadece $E$ diyelim)

  • Güncelle: $w_j := w_j + \lambda[F_j(x,y) - E]$

Bu hesabın en pahalı kısmı neresi? Beklenti hesabı. Bu beklentileri hesaplanması için daha önce verdiğimiz matris çarpımı yöntemine benzer bir yöntem kullanmak gerekiyor (burada vermeyeceğiz, arama motorunda Rahul Gupta üzerinden arayabilirsiniz, bu kişi bu konuyu anlatıyor).

Kaynak

[1] Elkan, Log-linear Models and Conditional Random Fields, http://videolectures.net/cikm08_elkan_llmacrf