K-Means Kümeleme Metodu
Popüler kümeleme algoritmalarından biri k-means algoritması. Bu metotta kaç tane kümenin olması gerektiği baştan tanımlanır ($k$ parametresi ile), algoritma bunu kendisi bulmaz. Metotun geri kalanı basit - bir döngü (iteration) içinde her basamakta:
1) Her nokta için, eldeki küme merkezleri teker teker kontrol edilir ve o nokta en yakın olan kümeye atanır.
2) Atamalar tamamlandıktan sonra her küme içinde hangi noktaların olduğu bilindiği için her kümedeki noktaların ortalaması alınarak yeni küme merkezleri hesaplanır. Eski merkez hesapları atılır.
3) Başa dönülür. Döngü tekrar ilk adıma döndüğünde, bu sefer yeni küme merkezleri kullanılarak aynı adımlar tekrarlanacaktır.
Fakat bir problem yok mu? Daha birinci döngü başlamadan küme merkezlerinin nerede olduğunu nereden bileceğiz? Burada bir tavuk-yumurta problemi var, küme merkezleri olmadan noktaları atayamayız, atama olmadan küme merkezlerini hesaplayamayız.
Bu probleme pratik bir çözüm ilk başta küme merkezlerini (ya da küme atamalarını) rasgele bir şekilde seçmektir. Pratikte bu yöntem çok iyi işliyor. Tabii bu rasgelelik yüzünden K-means'in doğru sonuca yaklaşması (convergence) garanti değildir, ama gerçek dünya uygulamalarında çoğunlukla kullanışlı kümeler bulunur. Bu potansiyel problemlerden kaçınmak için k-means pek çok kez işletilebilir (her seferinde yeni rasgele başlangıçlarla yani) ve aynı sonuca ulaşılıp ulaşılmadığı kontrol edilebilir.
Pek en iyi k nasıl bulunur? SVD kullanarak grafiğe bakmak (bu yazının sonunda anlatılıyor) mesela, fakat en iyisi K-Means yerine GMM kulanmak! Bkz. yazı sonundaki referans.
K-Means EM algoritmasının bir türevi olarak kabul edilebilir, EM kümeleri bir Gaussian (ya da Gaussian karışımı) gibi görür, ve her basamakta bu dağılımların merkezini, hem de kovaryansını hesaplar. Yani kümenin "şekli" de EM tarafından saptanır. Ayrıca EM her noktanın tüm kümelere olan üyeliklerini "hafif (soft)" olarak hesaplar (bir olasılık ölçütü üzerinden), fakat K-Means için bu atama nihai (hard membership). Nokta ya bir kümeye aittir, ya da değildir.
EM'in belli şartlarda yaklaşıksallığı için matematiksel ispat var. K-Means akıllı tahmin yaparak (heuristic) çalışan bir algoritma olarak biliniyor. Sonuca yaklaşması bu sebeple garanti değildir, ama daha önce belirttiğimiz gibi pratikte faydalıdır. Bir sürü alternatif kümeleme yöntemi olmasına rağmen hala K-Means kullanışlı. Burada bir etken de K-Means'in çok rahat paralelize edilebilmesi. Bu konu başka bir yazıda işlenecek.
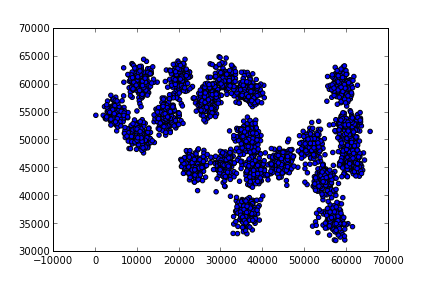
Örnek test verisi altta
import pandas as pd
data = pd.read_csv("synthetic.txt",names=['a','b'],sep=" ")
print data.shape
data = np.array(data)
(3000, 2)
plt.scatter(data[:,0],data[:,1])
plt.savefig('kmeans_1.png')
def euc_to_clusters(x,y):
return np.sqrt(np.sum((x-y)**2, axis=1))
class KMeans():
def __init__(self,n_clusters,n_iter=10):
self.k = n_clusters
self.iter = n_iter
def fit(self,X):
# her veri noktasi icin rasgele kume merkezi ata
labels = [random.randint(0,self.k-1) for i in range(X.shape[0])]
self.labels_ = np.array(labels)
self.centers_ = np.zeros((self.k,X.shape[1]))
for i in range(self.iter):
# yeni kume merkezleri uret
for j in range(self.k):
# eger kume j icinde hic nokta yoksa, ortalama (mean)
# hesabi yapma, cunku o zaman nan degeri geliyor, ve
# hesabin geri kalani bozuluyor.
if len(X[self.labels_ == j]) == 0: continue
center = np.mean(X[self.labels_ == j],axis=0)
self.centers_[j,:] = center
# her nokta icin kume merkezlerine gore kume atamasi yap
self.labels_ = []
for point in X:
c = np.argmin(euc_to_clusters(self.centers_, point))
self.labels_.append(int(c))
self.labels_ = np.array(self.labels_)
cf = KMeans(k=5,iter=20)
cf.fit(data)
print cf.labels_
[3 3 3 ..., 2 2 2]
Üstteki sonucun içinde iki ana vektör var, bu vektörlerden birincisi içinde 2,0, gibi sayılar görülüyor, bu sayılar her noktaya tekabül eden küme atamaları. İkinci vektör içinde iki boyutlu $k$ tane vektör var, bu vektörler de her kümenin merkez noktası. Merkez noktalarını ham veri üzerinde grafiklersek (kırmızı noktalar)
plt.scatter(data[:,0],data[:,1])
plt.hold(True)
plt.ylim([30000,70000])
for x in cf.centers_: plt.plot(x[0],x[1],'rd')
plt.savefig('kmeans_2.png')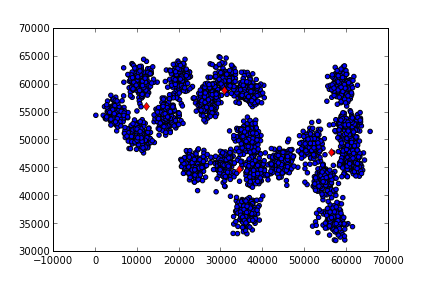
Görüldüğü gibi 5 tane küme için üstteki merkezler bulundu. Fena değil. Eğer 10 dersek
cf = KMeans(k=10,iter=30)
cf.fit(data)
plt.scatter(data[:,0],data[:,1])
plt.ylim([30000,70000])
plt.hold(True)
for x in cf.centers_: plt.plot(x[0],x[1],'rd')
plt.savefig('kmeans_3.png')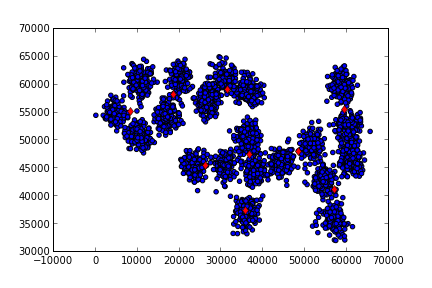
Kategorik ve Sayısal Öğeler İçeren Karışık Veriler
Bazen verimiz hem kategorik hem de sayısal (numeric) değerler içeriyor olabilir, KMeans yeni küme merkezlerini hesaplarken ortalama operasyonu kullandığı için sadece sayısal veriler üzerinde çalışabilir (kategorik verilerin nasıl ortalamasını alalım ki?). Bu durumda ne yapacağız?
Bir seçenek şu olabilir, kategorik her kolonu her değişik değeri bir yeni kolona tekabül edecek şekilde sağa doğru açarız, ve o değerin yeni kolonuna 1 değeri diğerlerine 0 değeri veririz. Bu kodlamaya 1-in-q kodlaması, 1-in-n kodlaması, ya da İngilizce 1-hot encoding ismi veriliyor.
Örnek olarak UCI veri bankasından Avustralya Kredi Verisine bakalım:
import pandas as pd
df = pd.read_csv("crx.csv")
print df[:2]
A1 A2 A3 A4 A5 A6 A7 A8 A9 A10 A11 A12 A13 A14 A15 A16
0 b 30.83 0.00 u g w v 1.25 t t 1 f g 00202 0 +
1 a 58.67 4.46 u g q h 3.04 t t 6 f g 00043 560 +
Bu veride A1, A2, gibi kolon isimleri var, kategorik olanlarda 'g','w' gibi değerler görülüyor. Bu kolonları değiştirmek için
from sklearn.feature_extraction import DictVectorizer
def one_hot_dataframe(data, cols):
vec = DictVectorizer()
mkdict = lambda row: dict((col, row[col]) for col in cols)
vecData = pd.DataFrame(vec.fit_transform(data[cols].to_dict(outtype='records')).toarray())
vecData.columns = vec.get_feature_names()
vecData.index = data.index
data = data.drop(cols, axis=1)
data = data.join(vecData)
return data
df2 = one_hot_dataframe(df,['A1','A4','A5','A6','A7','A9','A10','A12','A13'])
print df2.ix[0]
A2 30.83
A3 0
A8 1.25
A11 1
A14 00202
A15 0
A16 +
A10=f 0
A10=t 1
A12=f 1
A12=t 0
A13=g 1
A13=p 0
A13=s 0
A1=? 0
A1=a 0
A1=b 1
A4=? 0
A4=l 0
A4=u 1
A4=y 0
A5=? 0
A5=g 1
A5=gg 0
A5=p 0
A6=? 0
A6=aa 0
A6=c 0
A6=cc 0
A6=d 0
A6=e 0
A6=ff 0
A6=i 0
A6=j 0
A6=k 0
A6=m 0
A6=q 0
A6=r 0
A6=w 1
A6=x 0
A7=? 0
A7=bb 0
A7=dd 0
A7=ff 0
A7=h 0
A7=j 0
A7=n 0
A7=o 0
A7=v 1
A7=z 0
A9=f 0
A9=t 1
Name: 0, Length: 52, dtype: object
İşlem sonucunda A12=f mesela için 1 verilmiş, ama A12=t (ve diğer her mümkün değer için yani) 0 değeri verilmiş (sadece bu tek satır için). Böylece kategorik veriyi sayısal hale çevirmiş olduk.
Fakat işimiz bitti mi? Hayır. Şimdi KMeans bu tür veriyle acaba düzgün çalışır mıydı onu kendimize soralım. İçinde pek çok 0, bazen 1 içeren veri satırları arasında uzaklık hesabı yapmak ise yarar mı?
Yapay Öğrenim literatüründe bu tür veriler üzerinde kosinüs benzerliği (cosine similarity) kullanmak daha yaygındır. Bu konuyu {\em SVD, Toplu Tavsiye} yazısında daha iyi görülebilir. Kosinüs benzerliği bize 0 ile 1 arasında bir değer döndürür. Benzerliği uzaklığa çevirmek için basit bir şekilde 1-benzerlik formülünü kullanabiliriz. O zaman şöyle bir çözüm kullanabilir: normal sayısal değerler için Öklitsel, kategorik 1-hot kodlanmış kolonlar için Kosinüs uzaklığı kullanılır, bu uzaklıklar bazı ağırlıklar üzerinden birleştirilir, ve KMeans bu uzaklık ile iş yapar. Teknik olarak imkansız değil; KMeans merkez bulmak için ortalama alır ve Kosinüs uzaklığının verdiği aradaki açı, ortalama alma işlemi ile uyumludur. Yani içinde hem Öklitsel hem 1-hot kodlanmış verilerin olduğu vektörlerin ortalamasını alabiliriz, demek ki KMeans işleyebilir.
Problem şudur, iki uzaklığı birleştiren ağırlıklar ne olmalıdır? Bu yöntemi denediğimizde bu ağırlıkların ne seçildiğinin çok önemli olduğunu farkettik, ve kümeleme gibi denetimsiz (unsupervised) bir yöntemde bu hiperparametreleri deneme / yanılma yöntemi ile bulma şansımız yoktur.
Bu durumda kullanılabilecek bir yöntem şudur: SVD kullanarak tüm matrisi azaltmak ve onun üzerinde pür Öklitsel uzaklıklar kullanmak. Sayısal ve kategorik karışık verileri içeren verileri kümelemek için tavsiye edilen yöntem şudur:
1) Kategorik veriler üzerinde 1-hot kodlama yap.
2) Önce kolonları sonra satırları normalize et.
3) Tüm matris üzerinde çok küçük olmayan bir $k$ ile SVD al (mesela alttaki veri seti için önce 10)
4) $S$ vektörüne bak, ortalamadan büyük olan kaç tane hücre olduğunu gör.
5) Bu sayı yeni $k$ değerimiz olacak, SVD'yi tekrar bu $k$ ile işlet.
6) Elde edilen $U$ üzerinde kümeleme yap,
from sklearn.preprocessing import normalize
import scipy.sparse.linalg as slin
import scipy.linalg as lin
import pandas as pd
df = pd.read_csv("crx.csv",sep=',',na_values=['?'])
df = df.dropna()
df['A16'] = df['A16'].str.replace('+','1')
df['A16'] = df['A16'].str.replace('-','0')
df['A16'] = df['A16'].astype(int)
df2 = one_hot_dataframe(df,['A1','A4','A5','A6','A7','A9','A10','A12','A13'])
df2 = df2.drop('A16',axis=1)
df2 = np.array(df2)
df3 = df2.copy()
df3 = normalize(df3, norm='l2', axis=0)
df3 = normalize(df3, norm='l2', axis=1)
u,s,v=slin.svds(df3,k=10)
print s
[ 4.45826083 4.49654025 4.68382638 4.93391665 4.98604314
5.153349 5.63521289 5.70490968 6.68558115 14.81145675]
Bakıyoruz, averajdan yüksek olan en büyük sadece iki kolon var. SVD literatüründe bu kolonların matrisin "enerjisini" içerdiği söylenir, hakikaten eğer SVD ayrıştırma sonrası bu ilk kolona bu kadar önem verdiyse, onlar önemli, "enerjiyi içeriyor" olmalıdırlar. Şimdi SVD'yi $k=2$ ile tekrar işletiyoruz,
u,s,v=slin.svds(df3,k=2)
print s
[ 6.68558115 14.81145675]
Şimdi $U$ üzerinde kümeleme yapacağız, ve kontrol için kenara koyduğumuz bilinen etiketler üzerinden kümeleme başarımızı ölçeceğiz. Avustralya Kredi Verisi aslında izlenen (supervised) algoritmalar için kullanılır, ama biz onu izlenmeyen kümeleme problemi için kullandık, bilinen etiketleri veri içinden çıkartıp bir kenara koyuyoruz, ve sonra kümeleme tahmini yaparak bu etiketlerle olan uyumu ölçüyoruz.
clf = KMeans(n_clusters=2)
clf.fit(u)
labels_true = np.array(df['A16'])
labels_pred = clf.labels_
match = np.sum((labels_true == labels_pred).astype(int))
print float(match)/len(df), 1-float(match)/len(df)
0.217457886677 0.782542113323
Başarı yüzde \%78. Çok iyi. Üstteki örnek küme sayısının (dikkat SVD $k$'sinden farklı) bilindiğini farz etti. Bazı durumlarda küme sayısını grafiksel olarak görmek mümkündür (ama en iyisi Gaussian Karışım Modeli kullanıp mümkün K'leri AIC ile test etmek, bkz {\em İstatistik, GMM ile Kümelemek} yazısı).
Mesela üstteki veri seti için ortalamayı çıkartıp varyansa bölersek ve SVD işletirsek en büyük iki $U$ kolonun grafiği alttaki gibi çıkıyor,
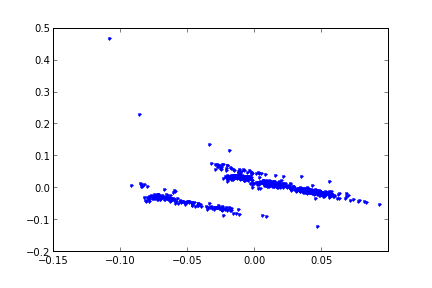
Eğer rasgele yansıtma (random projection) kullansaydık ne olurdu? Bu işlemi
birkaç kez yapalım ki rasgele matris Omega değişik şekillerde (ama
hala rasgele) üretilince sonuç değişir miydi görelim.
import numpy.random as rand
for i in range(5):
Omega = rand.randn(df3.shape[1],30)
u = np.dot(df3,Omega)
clf = KMeans(n_clusters=2)
clf.fit(u)
labels_true = np.array(df['A16'])
labels_pred = clf.labels_
match = np.sum((labels_true == labels_pred).astype(int))
print float(match)/len(df), 1-float(match)/len(df)
0.436447166922 0.563552833078
0.258805513017 0.741194486983
0.367534456355 0.632465543645
0.390505359877 0.609494640123
0.456355283308 0.543644716692
Görüldüğü gibi bazen çok iyi sonuçlar alıyor olsak bile bazen çok kötü sonuçlar da alabiliyoruz. Demek ki bu veri setinde SVD tekniği daha başarılı.
Kaynaklar
[1] Corrada, Practicum: Kernelized K-means, nbviewer.ipython.org/url/cbcb.umd.edu/~hcorrada/PML/src/kmeans.ipynb
[2] UCI Machine Learning Repository, Statlog (Australian Credit Approval) Data Set , https://archive.ics.uci.edu/ml/datasets/Statlog+%28Australian+Credit+Approval%29
Yukarı