Zeki arama yazısında, arama algoritmasına tahmin yeteneği kazandırdığımızda problem sonucuna ulaşım hızını arttırmıştık. Tahmin yeteneği oyun tahtasına değer biçebilen işlev sayesinde bilgisayara kodlanmıştı.
Bir soru; İnsan zekasında tahmin neye dayanır? Üzerinde bilgimiz, tecrübemiz olmayan konu hakkında tahmin yapabilirmiyiz? Hayır. Öyleyse bilgisayara tahmin özelliği kazandırdığımız zaman aynı zamanda makinaya “bilgi” verdiğimizi söyleyebiliriz. Makinayı bilgilendirdik, ona tecrübe kazandırdık da diyebiliriz çünkü tahmin, bir konu hakkında bilgimize, tecrübemize dayandığı ölçüde başarılı olabilir.
Bilgisayara bilgiyi iki şekilde verebiliriz: Yapısal, ya da işlevsel. Zeki arama örneği işlevsel bir örnek gösterdi. Bilgiyi, bilgisayara algoritma halinde verdik. Tahta değerlendiren işlev, her taşa göre nasıl hesap yapacağını biliyordu. Bu hesabı toplama ve çarpma işlemlerini kullanarak ve daha önceden “bildiği” ağırlıklara göre birbirine ekleyerek tahta hakkında ne düşündüğünü tek bir sayı halinde bildirdi, ve algoritmanın geri kalanı bu değerler ile doğru seçimi yaparak sonuca ulaştı.
Bu yazıda oyun oynama yerine birçok seçeneğin arasında karar vermek konusunu işleyeceğiz. Zeki aramanın aksine bilgi bilgisayara işlev olarak değil, bir karar ağaç yapısı olarak verilecek, ve daha da iyisi bilgisayarın bu yapıyı “örnek veriden” kendi kendine öğrenmesi sağlanacak.
Karar Ağacı Nedir?
Video, televizyon gibi bir ev elektronik eşyasının kılavuzunda “şu, şöyle olduysa şöyle yap” gibi tarifler vardir. İlk önce kontrol edilmesi tavsiye edilen ayarlar vardır, ve bu ayarlardan gelen cevaba göre değişik ayarlara bakılması tavsiye edilir ve en sonunda kılavuz ne hangi özel düğmeye basılması gerektiğini söyler. Kullanım kılavuzları onlarca sayfalık bir karar ağacıdır denebilir. İnsanlara karar ağacın kavramı doğal geldiği için kılavuzlar bu şekilde hazırlanmıştır.
Diğer bir örnek, lokantalarda çok yemek yiyen birisinin kullandığı karar ağacı olabilir. Bu kimse her türlü değişik şart altında değişik lokantalara gitmiş, ve her seferindeki memnuniyet/pişmanlık durumunu kayıt ederek bir karar ağacı oluşturmuş ise, artık yeni bir lokantada karar kılması için kapısından şöyle içeri bakıp menüye göz gezdirmesi yeterli olacaktır. Bu kişinin lokanta deneyimleri mesela aşağıdaki gibi kayıtlı olsun.
labels = ['BASKA','BAR','HAFTASONU','ACMIYIZ','MUSTERILER',\
'FIYAT','YAGMUR', 'RESERVASYON','YEMEKTURU','BEKLEMESURESI','BEKLEYELIM']
dataSet = [
['EVET','HAYIR','HAYIR','EVET','BIRAZ','DDD','HAYIR','EVET','FRANSIZ','0','EVET'],
['EVET','HAYIR','HAYIR','EVET','DOLU','D','HAYIR','HAYIR','TAYLAND','30','HAYIR'],
['HAYIR','EVET','HAYIR','HAYIR','BIRAZ','D','HAYIR','HAYIR','KEBAP','0','EVET'],
['EVET','HAYIR','EVET','EVET','DOLU','D','EVET','HAYIR','TAYLAND','10','EVET'],
['EVET','HAYIR','EVET','HAYIR','DOLU','DDD','HAYIR','EVET','FRANSIZ','60','HAYIR'],
['HAYIR','EVET','HAYIR','EVET','BIRAZ','DD','EVET','EVET','ITALYAN','0','EVET'],
['HAYIR','EVET','HAYIR','HAYIR','HIC','D','EVET','HAYIR','KEBAP','0','HAYIR'],
['HAYIR','HAYIR','HAYIR','EVET','BIRAZ','DD','EVET','EVET','TAYLAND','0','EVET'],
['HAYIR','EVET','EVET','HAYIR','DOLU','D','EVET','HAYIR','KEBAP','60','HAYIR'],
['EVET','EVET','EVET','EVET','DOLU','DDD','HAYIR','EVET','ITALYAN','10','HAYIR'],
['HAYIR','HAYIR','HAYIR','HAYIR','HIC','D','HAYIR','HAYIR','TAYLAND','0','HAYIR'],
['EVET','EVET','EVET','EVET','DOLU','D','HAYIR','HAYIR','KEBAP','30','EVET']
]Peki bu veriye bakarak karar ağacını nasıl oluşturacağız?
İnsanın aklında karar ağacını oluşturması başka bilim dalları altında araştırılıyor. Bilgisayar için karar ağacını “kendi kendine çıkartan” bir yapay zeka algoritması (ID3), bu yazımızın konusu olacak. ID3 ve genelde öğrenen algoritmalar ve ileride mekanize-öğrenme konusuna giriş açısından yararlı olabilir, ve bu konuda zaten en popüler yaklaşım olan ID3’ün geniş bir uygulama alanı vardır.
Algoritma
Karar ağacımız öyle olsun ki, eğitim verisi ile eğitildikten sonra, yeni bir soruya karşılılk, üstten başlayarak yeni şartlar çerçevesinde (ama eski veriye göre kurulmuş) ağaçta bizi bir ‘evet’ ya da ‘hayır’ cevabına doğru yönlendirsin. İyi kurulmuş bir karar ağacı, “en az” soru ile “en çabuk” cevaba erişmemizi sağlayan ağaçtır. Çünkü ileride de göreceğimiz gibi, aynı veri için birden fazla değişik karar ağacı kurmak mümkündür.
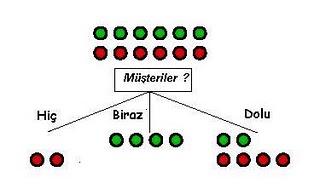
Evet, algoritmamıza başlayalım. Veriyi bölmek için, bir başlık seçmemiz gerekiyor. Bu seçimi şimdilik rasgele yapalım, diyelim ki “Müşteri” başlığını seçtik. Veriye bakınca, bu başlık altında “Hiç”, “Biraz” ya da “Dolu” değerlerini görüyoruz. Bu başlığı en üst düğüm olarak ağaca yerleştirelim, ve veriyi, bu başlığın tekrar eden değerlere göre guruplayıp, bölelim.
Alttaki ağaç, müşteri başlığı üzerinden oluşturulan ağacımızın ilk seviyesidir.

Yeşil ve kırmızı toplar evet=yeşil, hayır=kırmızı cevaplarını temsil ediyorlar. Resimin anlatmak istediği, karar ağacı öğreniminin, eğitim verisinin tamamını böldüğü, ve seçenekler arasında taksim ettiği. Elimizdeki verinin “hedef başlığı” “bekleyelim mi?” sorusudur, ve cevabı sadece evet ya da hayır olabilir. Yazının geri kalan kısmında kırmızı ve yeşil topların hepsini göstermeyeceğiz. Kolaylık bakımından ağacın en uç kısmında tamamen yeşil ya da tamamen kırmızı var ise tek bir renk göstermek yeterli olacak.
Ağacın bu ilk seviyesine bakınca, görüyoruz ki daha şimdiden elimizde yararlı bir karar ağacı var. Çünkü eğer, ‘müşteriler’ sorusuna yeni sorunun cevabı “hiç” olsaydı, direk olarak bir “Y” (Yanlış) cevabına erişmemiz mümkün oluyordu. Bu noktada iş bitiyor, karar verilmiş olurdu. Tabii bu cevap senaryosu çok iyimser bir senaryodur, çünkü eğer yeni sorunun cevabı “Dolu” olsa idi, bu dalı izleyerek hala bölünmüş olan bir dala geldiğimizi görecektik. Demek ki ağaç oluşturan algoritmanın işi daha bitmedi. “Dolu” dalını takip ederek, oradaki verileri de bölmeye devam etmemiz gerekiyor.
Bu dalı bölmek için, ‘müşteriler’ başlığından sonra, gene rasgele olarak, ‘bekleme süresi’ başlığını seçebiliriz. Eğer lokanta dolu ise, kapıda beklememiz için eğitim verisinde elimizde olan bekleme süreleri bu başlık altında toplanmış. Mümkün değerler 60 dakika’dan fazla, 30-60 dakika arası, 10-30 dakika arası, ya da 10 dakikadan daha az beklemek olarak görülüyor. Bu bölünmeyi de yaptıktan sonra, sırası ile “müşteriler=dolu’’ ve”bekleme süresi=60 dakidan fazla’’ sorusunun bizi kesin bir cevaba eriştirdiğini göreceğiz. Ayrıca, “müşteriler=dolu’’ ve”10 dakikadan az beklemek’’ sorusu bizi ‘evet’ cevabına getirecektir. Bunlar da güzel. Fakat işimiz daha bitmedi, halâ bölünmemiş dallar var, vs.
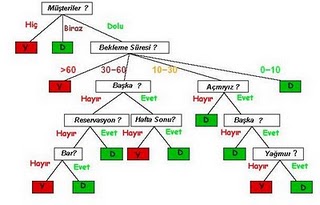
Herhalde algoritmanın bölen ve ağaç oluşturan kısmının mantığı anlaşıldı. Tahmin edilecegi gibi bu bölme ve dal oluşturma işlemi tamamen ‘evet’ ve ‘hayır’ sonuçlarına erişinceye kadar devam edecek. Sonuç karar ağacını aşağıda görüyoruz.
Optimizasyon
Yapay zeka dalında, algoritmaların doğruluğu kadar, bilgisayara getirdiği yükün ne kadar önemli olduğunu görmüştük. O kadar ki, eğer bu yük kontrol edilir bir ölçüde değil ise, algoritmanın işe yararlılığı sorgulanmaya başlanır. Test olarak, bir algoritmanın 12 veri satırı (yukarıdaki örnek) yerine , 500,000 satırlık veri ile ne yapacağını sormak yerinde olur. Çünkü insan beyninin yaptığı binbir türlü teknik kullanarak bu kadar veriyi işlemektir, aktif zekamızda farkında olmasak bile, belli bir seviyede bu işlemler olmaktadır. Basit bir iş gibi görünen bir yerden bir yere kalkıp yürümek için kullandığımız algoritmaların neler çözmek zorunda olduğunu, robot yazılımlar ile uğraşanlar bilir.
O yüzden, ID3 algoritmasını 500,000 satırlık veriyi idare edebilecek şekilde ilerletmemiz gerekiyor.
Başlık Seçimi
Ilerletme için uygun bir zaman herhalde başlık seçimi esnâsında olacaktır. İlk karar ağacında gördüğümüz gibi bazı sorulara olan cevaplar daha ilk seviyede kesin cevaba erişebiliyordu. Demek ki, sürekli olarak “uygun başlığı uygun zamanda” seçersek, ağacımızı oldukça küçültmemiz mümkün olur. Böylece kesin cevaba erişmemiz kolaylaşır. Tabii kolaylık derken, 500,000 satırlık veri için 100 derinliğindeki bir ağaç ile 10 birim arasındaki bir farktan bahsediyorum, ki bu fark hiç yabana atılacak bir fark değildir.
Peki uygun başlık nedir? Mesela ilk seviye için, müşteri yerine, “yemek türü” başlığını seçseydik, daha mı iyi bir seçim yapmış olurduk? Bu farazi bölünmeyi aşağıdaki şekilde görelim.
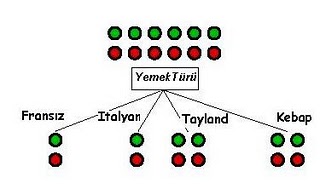
Görüyoruz ki, bu yeni bölünme bizi hiç bir kesin cevaba götürmedi. Üstüne üstlük, bütün bu dalların alt-dalları, onlarında alt-dalları derken ağacımızın arap saçına dönmesi ihtimal dahilinde. Demek ki ‘yemek türü’ bölünmesi bize yeni “bilgi” sâğlamadı. Halâ elimizde kesin cevaplar değil, seçenekler var.
Bize öyle bir işlev lazım ki, her parçaya bakıp kazandırdığı bilgiyi ölçsün, hala bölünmüş kalan kısımlar içinde bile, onlardan en iyi olanını seçsin. İşte bu noktada bilgi kuramı yardımımıza yetişiyor.
Bilgi Kuramı
Bilgi kuramı (information theory), bilgiyi nasıl kodlayacağımızı ve sonuç kodlamanın ne kadar yer tutacağı gibi sorunlar ile uğraşır. Mesela, elimizde 2 değişik değer var ise ve bu değerleri ikili düzende kodlamamız gerekse, bu iş için kaç tane bit gerekir?
Cevap: Bir tane.
Peki, 4 tane değer olduğunu düşünelim. Şimdi kaç tane? Cevap: İki. Tekrar eden mantık belki farkedilmistir; eğer “kaç bit” sorusu ile “eldeki bilgi” arasında matematiksel bir bâglantı kurmak gerekse (K ye B), şöyle yazabiliriz. Parça Bilgi Değeri şuna eşit:
\[ -\frac{d}{d+y} \log_2 \bigg( \frac{d}{d+y} \bigg) - \frac{y}{d+y} \log_2 \bigg( \frac{y}{d+y} \bigg) \]
Adresleme, onluk düzen ve ikilik düzen arasında gidip gelme gibi problemlerden hatırlayabileceğimiz bir sonuç bu. Ya da, ‘iki tane bit en fazla kaç onluk sayıyı gösterir’ sorusunun tersten sorulmuş şeklidir denebilir.
Şimdi bu ters soruyu karar ağacının böldüğü her parçaya soralım.
Tabii birkaç değişiklik yapmamız gerekecek. Mesela elimizde
yemekturu=tayland sonucunda tek bir parça üzerine 2 yanlış
ve 2 doğru değer var ise, bu düğümün bilgi değerini kesirler ile
hesaplamamız gerekecek. Kesirler ile uğraşırken log işlevi eksi değerler
getireceği için cevabı önce kesirin kendisi, sonra da eksi ile çarpmamız
lazım (\(\log\), 0 ve 1 arası için eksi
değer getirir). Yani, genel olarak iki cevaplı bir uzayda, tek parçanın
bilgi değeri şöyle gösterilebilir. Parça Bilgi Değeri suna eşit:
\[ B(O(v_1),...,O(V_n)) = \sum_{i=1}^{n} -O(v_i)\log_2O(v_i) \]
\(O\), olasılığı temsil ediyor.
Genel olarak göstermek gerekirse, n cevaplı bir uzayda parçanın bilgi değeri şudur.
\[ B \bigg(\frac{1}{2}, \frac{1}{2} \bigg) = \frac{1}{2}\log_2 \bigg(\frac{1}{2} \bigg) - \frac{1}{2}\log_2 \bigg(\frac{1}{2} \bigg) = \textrm { 1 bit } \]
Formülü kontrol etmek için, başta verdiğimiz bit örneğini kullanalım: 2 değişik değer için kaç bit gerekir?
\[ \sum_{i=1}^{parca} \frac{d_i + y_i}{d+y} \bigg( \frac{d_i}{d_i+y_i}, \frac{y_i}{d_i+y_i} \bigg) \]
\(d_i\): i’inci parça doğru sayısı
\(y_i\): i’inci parca yanlis sayisi
\(d\): tüm doğrular
\(y\): tüm yanlışlar
1 bit gerektiğini halâ bulabiliyoruz.
Parçaların Bilgi Değer Toplamı
Bölündükten sonra elimize geçen parçaların bilgi değer toplamı için
Müşteri Parçaları
\[ \frac{2}{12}B(0,1) + \frac{4}{12}B(1,0) + \frac{6}{12} B(\frac{2}{6}, \frac{4}{6}) = 0.459 \]
Yemek Türü Parçaları
\[ \frac{2}{12}B(\frac{1}{2},\frac{1}{2}) + \frac{2}{12}B(\frac{1}{2},\frac{1}{2}) + \frac{4}{12}B(\frac{2}{4},\frac{2}{4}) + \frac{4}{12}B(\frac{2}{4},\frac{2}{4}) = 1 \]
Problemi sözel olarak biraz daha berraklaştıralım. Herhangi bir düğümde iken, bu düğümün bilgi değerini B() ile bulabiliriz. Lokanta örneğinin ilk seviyesinde, en üst düğümün bilgi değeri ‘1’ olduğunu görülebilir, çünkü elimizde tek düğüm, 6 yanlış, 6 doğru cevap var. Güzel.
Şimdi bir seviye aşağı inelim. Her başlığı teker teker deneyip, ve veriyi her başlık için geçici olarak parçalayıp, muhtemel her bölünme için bu başlığa tekâbül eden parçaların bilgi değerini toplayalım (bir üstteki formül).
Örnek veri üzerinde üstteki formülü deneyelim (1. seviye parçalanması için)
Müşteri Parçaları
\[ \frac{2}{12}B(0,1) + \frac{4}{12}B(1,0) + \frac{6}{12}B(\frac{2}{6}, \frac{4}{6}) = 0.459 \]
Yemek Türü Parçaları
\[ \frac{2}{12}B(\frac{1}{2}, \frac{1}{2}) + \frac{2}{12}B(\frac{1}{2}, \frac{1}{2}) + \frac{4}{12}B(\frac{2}{4}, \frac{2}{4}) + \frac{4}{12}B(\frac{2}{4}, \frac{2}{4}) = 1 \]
Görüyoruz ki, ağacın en üst seviyesini temsil etmek için 1 bit gerekiyor iken, müşteri bölünmesinden sonra 0.459 bit yetiyor (daha az). Fakat yemek türü bölünmesinden sonra halâ 1 bit lâzım! Yani, yemek türü bölünmesi bize hiç bir şey kazandırmadı.
Kazanç kelimesini aritmetik olarak şöyle târif edebiliriz: Bir düğümün bilgi değerinden, bu düğümün alt-parçalarının bilgi değer toplamının düşülmesi kazanç değerini verir. ID3 algoritması, tabii ki daha az bit gerektiren ya da, daha çok bilgi “kazandıran” seçeneği takip ederse daha etkili olur. Böylece her seviyede gitgide daha berraklaşan karar ağacı, “en az” seviyede, kesin kararlara “en çabuk” şekilde ulaşan karar ağacı olacaktır.
Eğer B() işlevinin iç mekanizmaları hala anlaşılmadı ise, şunları bilmek yardımcı olabilir:
Parça tamamen yanlış değerler içeriyor (kesin cevap) = B(0,1) = 0 bit
Parça tamamen doğru değerler içeriyor (kesin cevap) = B(1,0) = 0 bit
… 3 doğru, 3 yanlış = B(3,3) = 1 bit … 2 doğru, 4 yanlış = B(2,4) = 0.92 bit … 1 doğru, 5 yanlış = B(1,5) = 0.65 bit
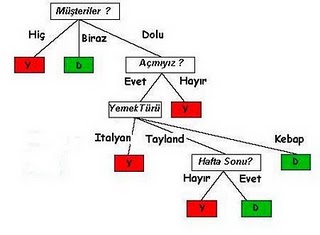
Yeni algoritmanın sonucu ortaya çıkacak karar ağacı şöyle olacaktır. Bu ağacın ilk baştaki ağaca kıyasla çok daha küçük olduğunu görüyoruz.
Kodu Python ile göstermek gerekirse [1]
from math import log
import operator
def calcShannonEnt(dataSet):
numEntries = len(dataSet)
labelCounts = {}
# kac ozgun deger var ve bu degerler kac kere ortaya cikiyorlar
for featVec in dataSet:
currentLabel = featVec[-1]
if currentLabel not in labelCounts.keys(): labelCounts[currentLabel] = 0
labelCounts[currentLabel] += 1
shannonEnt = 0.0
for key in labelCounts:
prob = float(labelCounts[key])/numEntries
shannonEnt -= prob * log(prob,2) #log base 2
return shannonEnt
def splitDataSet(dataSet, axis, value):
retDataSet = []
for featVec in dataSet:
if featVec[axis] == value:
reducedFeatVec = featVec[:axis]
reducedFeatVec.extend(featVec[axis+1:])
retDataSet.append(reducedFeatVec)
return retDataSet
def chooseBestFeatureToSplit(dataSet):
numFeatures = len(dataSet[0]) - 1
baseEntropy = calcShannonEnt(dataSet)
bestInfoGain = 0.0; bestFeature = -1
# tum ozellikleri ziyaret et
for i in range(numFeatures):
featList = [example[i] for example in dataSet]
uniqueVals = set(featList)
newEntropy = 0.0
for value in uniqueVals:
subDataSet = splitDataSet(dataSet, i, value)
prob = len(subDataSet)/float(len(dataSet))
newEntropy += prob * calcShannonEnt(subDataSet)
# enformasyon kazancini hesapla, yani entropideki azalisi
infoGain = baseEntropy - newEntropy
# bu hesabi simdiye kadarki en iyi kazancla karsilastir
if (infoGain > bestInfoGain):
bestInfoGain = infoGain
bestFeature = i
return bestFeature
def createTree(dataSet,labels):
classList = [example[-1] for example in dataSet]
if classList.count(classList[0]) == len(classList):
# tum siniflar esitse bolmeyi durdur
return classList[0]
if len(dataSet[0]) == 1:
return majorityCnt(classList)
bestFeat = chooseBestFeatureToSplit(dataSet)
bestFeatLabel = labels[bestFeat]
myTree = {bestFeatLabel:{}}
del(labels[bestFeat])
featValues = [example[bestFeat] for example in dataSet]
uniqueVals = set(featValues)
for value in uniqueVals:
#copy all of labels, so trees don't mess up existing labels
subLabels = labels[:]
myTree[bestFeatLabel][value] = \
createTree(splitDataSet(dataSet, bestFeat, value),subLabels)
return myTree
def getNumLeafs(myTree):
numLeafs = 0
# FIX: Convert dict_keys to a list
firstStr = list(myTree.keys())[0]
secondDict = myTree[firstStr]
for key in secondDict.keys():
if type(secondDict[key]).__name__=='dict':
numLeafs += getNumLeafs(secondDict[key])
else: numLeafs +=1
return numLeafs
def getTreeDepth(myTree):
maxDepth = 0
# FIX: Convert dict_keys to a list
firstStr = list(myTree.keys())[0]
secondDict = myTree[firstStr]
for key in secondDict.keys():
if type(secondDict[key]).__name__=='dict':
thisDepth = 1 + getTreeDepth(secondDict[key])
else: thisDepth = 1
if thisDepth > maxDepth: maxDepth = thisDepth
return maxDepth
def plotNode(nodeTxt, centerPt, parentPt, nodeType):
createPlot.ax1.annotate(nodeTxt, xy=parentPt, xycoords='axes fraction',
xytext=centerPt, textcoords='axes fraction',
va="center", ha="center", bbox=nodeType, arrowprops=arrow_args )
def plotMidText(cntrPt, parentPt, txtString):
xMid = (parentPt[0]-cntrPt[0])/2.0 + cntrPt[0]
yMid = (parentPt[1]-cntrPt[1])/2.0 + cntrPt[1]
createPlot.ax1.text(xMid, yMid, txtString, \
va="center", ha="center", rotation=30)
def plotTree(myTree, parentPt, nodeTxt):
numLeafs = getNumLeafs(myTree)
depth = getTreeDepth(myTree)
# FIX: Convert dict_keys to a list here as well
firstStr = list(myTree.keys())[0]
cntrPt = (plotTree.xOff + (1.0 + float(numLeafs))/2.0/plotTree.totalW,\
plotTree.yOff)
plotMidText(cntrPt, parentPt, nodeTxt)
plotNode(firstStr, cntrPt, parentPt, decisionNode)
secondDict = myTree[firstStr]
plotTree.yOff = plotTree.yOff - 1.0/plotTree.totalD
for key in secondDict.keys():
if type(secondDict[key]).__name__=='dict':
plotTree(secondDict[key],cntrPt,str(key))
else:
plotTree.xOff = plotTree.xOff + 1.0/plotTree.totalW
plotNode(secondDict[key], (plotTree.xOff, plotTree.yOff), \
cntrPt, leafNode)
plotMidText((plotTree.xOff, plotTree.yOff), cntrPt, str(key))
plotTree.yOff = plotTree.yOff + 1.0/plotTree.totalD
def createPlot(inTree):
fig = plt.figure(1, facecolor='white')
fig.clf()
axprops = dict(xticks=[], yticks=[])
createPlot.ax1 = plt.subplot(111, frameon=False, **axprops)
plotTree.totalW = float(getNumLeafs(inTree))
plotTree.totalD = float(getTreeDepth(inTree))
plotTree.xOff = -0.5/plotTree.totalW; plotTree.yOff = 1.0;
plotTree(inTree, (0.5,1.0), '')
plt.savefig('id3_1.png')
decisionNode = dict(boxstyle="sawtooth", fc="0.8")
leafNode = dict(boxstyle="round4", fc="0.8")
arrow_args = dict(arrowstyle="<-")
tree = createTree(dataSet, labels)
createPlot(tree)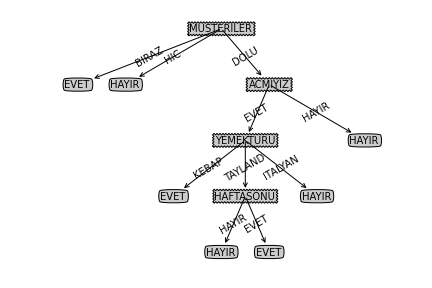
Aynı kodu LİSP ile görelim,
;;
;; Ilk kolon, her satir icin kimlik gorevini yapiyor. Yani, d1'i
;; kullanarak d1 ile baslayan tum veri satirina ulasmak mumkun.
;; Python kodundaki veri farkli olarak ikinci kolondaki etiket degerini
;; en sona atiyor
;;
;; LISP dilinde bu isi gerceklestirebilmek icin, veri satirindaki bilgileri
;; anahtar-deger deger cifti olarak kimlik kolonu 'uzerinde' sakliyoruz.
;; LISP komutlarindan 'get', bu isi goruyor.
;;
(setf *egitim-verisi*
'(
(d1 EVET EVET HAYIR HAYIR EVET BIRAZ DDD HAYIR EVET FRANSIZ T0)
(d2 HAYIR EVET HAYIR HAYIR EVET DOLU D HAYIR HAYIR TAYLAND T30)
(d3 EVET HAYIR EVET HAYIR HAYIR BIRAZ D HAYIR HAYIR KEBAP T0)
(d4 EVET EVET HAYIR EVET EVET DOLU D EVET HAYIR TAYLAND T10)
(d5 HAYIR EVET HAYIR EVET HAYIR DOLU DDD HAYIR EVET FRANSIZ T60)
(d6 EVET HAYIR EVET HAYIR EVET BIRAZ DD EVET EVET ITALYAN T0)
(d7 HAYIR HAYIR EVET HAYIR HAYIR HIC D EVET HAYIR KEBAP T0)
(d8 EVET HAYIR HAYIR HAYIR EVET BIRAZ DD EVET EVET TAYLAND T0)
(d9 HAYIR HAYIR EVET EVET HAYIR DOLU D EVET HAYIR KEBAP T60)
(d10 HAYIR EVET EVET EVET EVET DOLU DDD HAYIR EVET ITALYAN T10)
(d11 HAYIR HAYIR HAYIR HAYIR HAYIR HIC D HAYIR HAYIR TAYLAND T0)
(d12 EVET EVET EVET EVET EVET DOLU D HAYIR HAYIR KEBAP T30)
))
(setf *dogru-sayisi* 0)
(setf *yanlis-sayisi* 0)
(setf *toplam-veri-sayisi* 0)
(setf *basliklar*
'(BEKLEYELIMMI
BASKA
BAR
HAFTASONU
ACMIYIZ
MUSTERILER
FIYAT
YAGMUR
RESERVASYON
YEMEKTURU
BEKLEMESURESI))
(defun deger-koy (baslik satir deger)
(setf (get satir baslik) deger))
(defun deger-al (baslik satir)
(get satir baslik))
;; uzerinde irdeleme yaptigimiz kolon degerini bulup geri
;; getirir.
(defun hedef-baslik-degeri (satir)
(get satir 'BEKLEYELIMMI))
(defun hedef-baslik () (return 'BEKLEYELIMMI))
(defun veriyi-satirkimligine-cevir (ornekler)
(loop for satir in ornekler collect
(car satir)))
;; verileri olusturan butun satirlarin irdeleme sonucu ayni mi?
;; yani, verilen satilarinin hepsinin 'bekleyelimmi ozelligi
;; ayni cevabi mi tasiyor?
(defun ayni-cevap? (satirlar)
( let ((sonuc nil))
(setq ilkdeger (hedef-baslik-degeri (car satirlar)))
(setf sonuc (every #'(lambda(e)
(equal ilkdeger (hedef-baslik-degeri e)))
(cdr satirlar))
) sonuc ))
;; bu islevin, program basladiktan hemen sonra cagrilmasi
;; gerekiyor. anahtar/deger bilgilerini bu fonksiyon yaratip,
;; kimlik sembolu uzerine koyuyor
(defun egitim-verilerini-cevir (veri basliklar)
(loop for d in veri do
(loop for baslik in basliklar
as deger in (cdr d)
do
(setf kimlik-no (first d))
(deger-koy baslik kimlik-no deger)
))
(loop for d in veri do
(if (equal (hedef-baslik-degeri (car d)) 'EVET) (incf *dogru-sayisi*))
(if (equal (hedef-baslik-degeri (car d)) 'EVET) (incf *yanlis-sayisi*))
)
(setf *toplam-veri-sayisi* (+ *dogru-sayisi* *yanlis-sayisi*))
)
;;
;;
;; Iste Algoritma
;;
;;
(defun karar-agaci-egit (ornekler basliklar)
(let ((sonuc nil))
;; ornekler, butun egitim verisini olusturur
(cond
((equal basliklar nil)
(setf sonuc (encok-gorulen-deger ornekler)))
;; butun satirlarin klasmani ayni ise, bulunan bu klasmani getir
;; hepsi ayni ise, herhangi birinin klasmani yeter
((ayni-cevap? ornekler)
(setf sonuc (hedef-baslik-degeri (car ornekler))))
;; Burada, parca listelerinin listesini olustur. Bu kocaman liste
;; elimizdeki veriyi her basligi kullanrak bolmus ve biraraya
;; konulmus bir halidir. parca-sec islevi, girdisini boyle bekliyor.
(t (progn
(setq parca-listenin-listesi
(loop for baslik in basliklar collect (parcala ornekler baslik)))
(setf eniyi (parca-sec parca-listenin-listesi))
(setf sonuc (cons (car eniyi)
(loop for dal in (cdr eniyi) collect
(list (car dal)
(karar-agaci-egit
(cdr dal)
(remove (car eniyi) basliklar))
))
))
))
) sonuc ))
(defun kazanc (parca-listesi)
(let ((kazanc 0))
;; Burada ufak bir numaraya dikkat. Gecici bir sekilde, parcalari
;; "butun" tek parcaya topluyoruz ki bolunmeden onceki bilgi
;; icerigini hesaplayabilelim.
(setf birlesim (reduce #'append (cdr parca-listesi)))
(setf ust-bilgi-icerigi
(parca-bilgi-icerigi birlesim))
(setf cocuklarin-bilgi-icerigi (bilgi-icerigi parca-listesi))
(setf kazanc (- ust-bilgi-icerigi cocuklarin-bilgi-icerigi))
kazanc ))
(defun bilgi-icerigi (parca-listesi)
;; her parcanin bilgi icerigini hesaplayip bu degerleri topla
(let ((toplam 0))
(dolist (parca (cdr parca-listesi)) ;; cdr komutu baslik kismini kesip atiyor
(incf toplam
(parca-bilgi-icerigi parca))
) toplam ))
(defun encok-gorulen-deger (baslik satirlar)
(let ((enuzun nil))
(loop for p in (parcala baslik satirlar) do
(when (> (length p) length)
(setq length (length p))
(setq enuzun p)))
(car enuzun)))
(defun parca-bilgi-icerigi (parca)
;; bu parca icindeki dogru ve yanlis satirlari say. Dogru
;; ve yanlis 'hedef basligina' gore bulunuyor tabii
(let ((dogru-sayisi 0)(yanlis-sayisi 0))
(dolist (kimlik-no parca)
(cond
;; eger satir BEKLEYELIMMI=EVET ise
((and (member kimlik-no parca)
(equal (hedef-baslik-degeri kimlik-no) 'EVET))
(incf dogru-sayisi))
;; eger satir BEKLEYELIMMI=HAYIR ise
((and (member kimlik-no parca)
(equal (hedef-baslik-degeri kimlik-no) 'HAYIR))
(incf yanlis-sayisi))
(t nil))
)
(setf toplam (+ dogru-sayisi yanlis-sayisi))
(setf dogru-orani (/ dogru-sayisi toplam))
(setf yanlis-orani (/ yanlis-sayisi toplam))
;; Asagida gorulan (zerop ..) kullanimi guzel bir LISP numarasi.
;; Eger dogru-orani 0 ise, hesabin geri kalani icin 0 kullan.
;; Fakat (zerop xx) 0 ise, yani xx 0 degil ise :), o zaman
;; log hesabini yap. Vay anasini.
;; Bu numaradan once 'sifirla bolunme (division by zero)' hatasi
;; aliyordum. log 0 hesap edilir bir deger degil demek ki,
;; tanim olarak 0 oldugu kabul ediliyor. Sinifta hoca da oyle
;; soylemisti.
(setf logp (* (* -1 dogru-orani)
(if (zerop dogru-orani) 0 (log dogru-orani 2))))
(setf logn (* (* -1 yanlis-orani)
(if (zerop yanlis-orani) 0 (log yanlis-orani 2))))
(setf log-toplam (+ logp logn))
(setf butune-olan-d-y-orani (/ toplam *toplam-veri-sayisi*))
(setf bilgi-icerik (* log-toplam butune-olan-d-y-orani))
bilgi-icerik ))
;;
;; veriyi bolmek icin en iyi basligi bul
(defun parca-sec (parca-listenin-listesi)
;;
;;
(let ((sonuc (car parca-listenin-listesi)))
(dolist (parca-listesi parca-listenin-listesi)
(if (> (kazanc parca-listesi)
(kazanc sonuc))
(setf sonuc parca-listesi)))
sonuc ))
;; karar agacina bunun ile soru sorabilirsin.
(defun soru-sor (satir agac)
(let (deger dal)
(if (atom agac) (return-from soru-sor agac))
(setf deger (deger-al (car agac) satir))
(setf dal (second (assoc deger (cdr agac))))
(soru-sor satir dal)))
;;
;; Verilen basliga gore veriye bakar, basligin altindaki verinin
;; tekabul eden degerine gore guruplama yapip, veriyi parcalara ayirir
(defun parcala (satirlar baslik)
(let ((gecici-liste ())(e nil)(kimlik-no nil)(bulunanlar-sayisi 0)(iteration 0))
(dolist (kimlik-no satirlar)
(setf dongu 0)
(setf bulunanlar-sayisi -1)
;; eger konol degeri zaten mevcut ise, kimlik-no'yi bu alt
;; listeye ekle
(dolist (su-anki-parca gecici-liste)
;; su anki parcanin ilk satirina bakmak yeterli, cunku
;; otekilerinde degeri ayni olacak
(setf su-anki-ornek-deger (car su-anki-parca))
;; degerler ayni ise
(if (equal su-anki-ornek-deger (deger-al baslik kimlik-no))
(progn
;; demekki satir bu parcaya ait. ekle.
(setf bulunanlar-sayisi dongu)
(return)
)
)
(incf dongu)
) ;; dolist sonu
(if (> bulunanlar-sayisi -1)
(progn
;; buraya dikkat edin; bir liste icerigini degil, gostergecini
;; (pointer) degistiriyoruz. Nth'in geri getirdigi, normal
;; deger degil, gostergec degeri. Yeni listenin gostergecini bu deger
;; uzerine yazinca, eski liste kaybolmus oluyor.
;; Yeni liste bir oncekinin bir fazlasi aslinda..
(setf (nth bulunanlar-sayisi gecici-liste)
(append (nth bulunanlar-sayisi gecici-liste) (list kimlik-no)))
))
;; yoksa, yeni bir alt-liste baslat, ve gecici-listeye ekle
(if (equal bulunanlar-sayisi -1)
(progn
(setf gecici-liste
(append gecici-liste
(list (list (deger-al baslik kimlik-no) kimlik-no))))
))
)
;; baslik degerini listenin onune koy
(setf gecici-liste (append (list baslik) gecici-liste))
gecici-liste
))
(defun agac-goster (agac &optional (derinlik 0))
(tab derinlik)
(format t "~A~%" (first agac))
(loop for alt-agac in (cdr agac) do
(tab (+ derinlik 1))
(format t "= ~A" (first alt-agac))
(if (atom (second alt-agac))
(format t " => ~A~%" (second alt-agac))
(progn (terpri)(agac-goster (second alt-agac) (+ derinlik 5))))))
(defun tab (n)
(loop for i from 1 to n do (format t " ")))
;; bu satiri silme
(egitim-verilerini-cevir *egitim-verisi* *basliklar*)
;;
;; testler
;;
;; test degerlendiren fonksiyon
(defun test (isim deyim sonuc)
(cond
((equal deyim sonuc) t)
(t (print isim) (error "HATA! Birim Testler Hata Yakaladi! "))
))
;; her sembolun bir ozellik listesi var
(test "ozellik listesi bos olan sembol" (get 'ornek-sembol 'baharatlar) NIL)
;; her sembolun bir ozellik listesi var
(setf (get 'ornek-sembol 'baharatlar) 'tuz)
(test "ornek sembole baska bir deger ekle" (get 'ornek-sembol 'baharatlar) 'tuz)
;; her sembolun bir ozellik listesi var
(setf (get 'ornek-sembol 'tatlilar) 'baklava)
(test "degisik bir sembole birsey ekle"
(get 'ornek-sembol 'tatlilar) 'baklava)
;; baslik degerini eriselim
(test "tablo dogru kuruldu" (hedef-baslik-degeri 'd1) 'EVET)
;; yemekturu uzerinde parcalara ayiralim
(setf beklenen-parcalar '(YEMEKTURU (FRANSIZ D1 D5)
(TAYLAND D2 D4 D8 D11)
(KEBAP D3 D7 D9 D12)
(ITALYAN D6 D10)))
(test "parcala (yemekturu)"
(parcala (veriyi-satirkimligine-cevir *egitim-verisi*) 'YEMEKTURU)
beklenen-parcalar)
;; musteriler uzerinde parcalara ayiralim
(setf beklenen-parcalar '(MUSTERILER (BIRAZ D1 D3 D6 D8)
(DOLU D2 D4 D5 D9 D10 D12)
(HIC D7 D11)))
(test "musteriler uzerinden parcala"
(parcala (veriyi-satirkimligine-cevir *egitim-verisi*) 'musteriler)
beklenen-parcalar)
;; bilgi icerigi
(setf *toplam-veri-sayisi* 12)
(test "bilgi icerigi" (parca-bilgi-icerigi
(veriyi-satirkimligine-cevir *egitim-verisi*))
1)
;; eniyi parcayi bul, MUSTERILER basliginin secilmesi lazim.
(setf yemekturu-parcalari
'(TYPE
(FRANSIZ D1 D5)
(TAYLAND D2 D4 D8 D11)
(KEBAP D3 D7 D9 D12)
(ITALYAN D6 D10)))
(setf musteri-parcalari
'(patrons
(BIRAZ D1 D3 D6 D8)
(TAYLAND D2 D4 D5 D9 D10 D12)
(HIC D7 D11)))
(setf ornek-girdi (list yemekturu-parcalari musteri-parcalari))
(test "parca-sec"
(parca-sec ornek-girdi) musteri-parcalari)
;; eniyi parcalamayi sec, MUSTERILER basliginin secilmesi lazim
(setf girdi '(D1 D3))
(test "ayni cevap 1" (ayni-cevap? girdi) t)
(setf girdi '(D2 D4))
(test "ayni cevap 2" (ayni-cevap? girdi) nil)
;; ana veriyi, kimlik no'lara cevir
(test "kimlik no ya ceviri testi" (veriyi-satirkimligine-cevir *egitim-verisi*)
'(D1 D2 D3 D4 D5 D6 D7 D8 D9 D10 D11 D12))
(setf agac (karar-agaci-egit (veriyi-satirkimligine-cevir *egitim-verisi*)
'(BASKA
BAR
HAFTASONU
ACMIYIZ
MUSTERILER
FIYAT
YAGMUR
RESERVASYON
YEMEKTURU
BEKLEMESURESI)
))
(agac-goster agac)
;; egitim verisinden bir satir kullanip soru sor
(test "soru-sor 1" (soru-sor 'd6 agac) 'EVET)
(test "soru-sor 2" (soru-sor 'd2 agac) 'HAYIR)
(test "soru-sor 3" (soru-sor 'd3 agac) 'EVET)
(test "soru-sor 4" (soru-sor 'd4 agac) 'EVET)
(test "soru-sor 5" (soru-sor 'd5 agac) 'HAYIR)
(test "soru-sor 6" (soru-sor 'd6 agac) 'EVET)
(test "soru-sor 7" (soru-sor 'd7 agac) 'HAYIR)
(test "soru-sor 8" (soru-sor 'd8 agac) 'EVET)
(test "soru-sor 9" (soru-sor 'd9 agac) 'HAYIR)
(test "soru-sor 10" (soru-sor 'd10 agac) 'HAYIR)
(test "soru-sor 11" (soru-sor 'd11 agac) 'HAYIR)
(test "soru-sor 12" (soru-sor 'd12 agac) 'EVET)
(print "Tamam. Birim Testler Isledi.")!clisp id3.lispMUSTERILER
= BIRAZ => EVET
= DOLU
ACMIYIZ
= EVET
YEMEKTURU
= TAYLAND
HAFTASONU
= HAYIR => HAYIR
= EVET => EVET
= ITALYAN => HAYIR
= KEBAP => EVET
= HAYIR => HAYIR
= HIC => HAYIR
"Tamam. Birim Testler Isledi." Kaynaklar
[1] Harrington, P., Machine Learning In Action