Yapay Ögrenime Giriş

Bu makalede, yapay öğrenim (machine learning) konusunun amacından, motive eden faktörlerden bahsedeceğiz, ve yapay öğrenimde istatistiki yöntemler ve grafik modelleri savunan/yeğleyen bir açı ile yaklaşmaya çalışacağız.

Yapay ögrenim, doğada görülen/gözlemlenen herhangi bir veriyi, veriden daha ufak şekilde temsil etmemize yardım eder. Ve bunları, gözlemlenen olay için net bir matematiksel model olmadığı zaman yapmaya uğraşır. Modeli bilgisayara oluşturttuktan sonra, bu modeli kullanarak, diğer yapay öğrenim araçlarını kullanmaya başlayabiliriz: Bunlar kümeleme (clustering), anormallik farketme (anomaly detection), regresyon (regression) ve özellik seçme (feature selection) gibi uygulamalardır.

YÖ'de iki ana kavram denetimli ve denetimsiz eğitim kavramı. Çok boyutlu bir girdiyle beraber onun etiketi, ya da eşlendiği bir hedef değeri var ise, ve algoritmamızı bu iki veriyi kullanarak eğitiyorsak, bu denetimli (supervised) bir eğitim. İstatistikteki regresyon aslında bir çeşit denetimli eğitim olarak görülebilir. İki boyutta çizgi uyduruyoruz, $x,y$ girdileri var, $x$ ana girdi, $y$ ise hedef / etiket. Ya da lojistik regresyonla bir email içeriği verisini o email spam'mı değil mi etiketi (0/1 değerleri ile) beraber eğitmek bir diğer örnek. Denetimsiz (unsupervised) eğitim örneği veriyi kümelere ayırmak; kümelemeyi başka bir veriden öğrenip bir diğerine uygulamıyoruz, elde hiç eğitilmiş bir yapı olmadan her veride mevcut kümeleri keşfetmeye uğraşıyoruz.

Bu makalede $\mathbf{x}$ vektörü bir boyuttaki girdiyi temsil etmek için, $\mathbf{X}$ çok boyutlu girdiyi temsil etmek için kullanılacak. Vektör $\mathbf{x}$'in bütün elemanları tek bir özelliği ölçen büyüklükler olarak kabul edelim, ve tersi belirtilmezse bağımsız özdeşçe dağılmış (iid) olarak görelim.

Regresyon Bazlı Yöntemler

Model

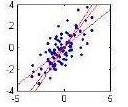
Yapay öğrenim için uygun bir başlangıç noktası, doğrusal regresyondur (linear regression). Veri olarak alınan $\mathbf{x}$ açıklamak için, hedef işlevi olarak eğriliği ve başlangıç noktasını bilmediğimiz bir doğru olan f(x)'i öğrenmeye çalışalım.

$$ f(x;\theta) = \sum_{i=1}^N \theta_{1}x_{i} + \theta_{0} \qquad (1) $$

ki $\theta_{0}$ ve $\theta_{1}$ bilinmeyen değişkenleri temsil ediyorlar. Birçok muhtemel $f(x;\theta)$ arasından araya araya en optimal $\theta$'yı bulmamız gerekiyor. Altta doğrusal regresyon grafini goruyoruz.

İlk önce (1)'i matris formuna çeviriyoruz, ki doğrusal cebir notasyonu kullanmamız mümkün olsun. Doğrusal cebir sayesinde, denklemi daha ileride çok boyutta işler hâle getirmek çok basit olacak.

$$ f(x;\theta) = \sum_{i=1}^N \left[ \begin{array}{cc} 1 & x_{i} \end{array} \right] \left[ \begin{array}{c} \theta_{0} \\ \theta_{1} \end{array} \right] \qquad (2) $$

$$ f(\mathbf{x};\theta) = \left[ \begin{array}{cc} 1 & x_{1} \\ \vdots \\ 1 & x_{N} \\
\end{array} \right] \left[ \begin{array}{c} \theta_{0} \\ \theta_{1} \end{array} \right] \qquad (3) $$

(2)'de gösterilen toplama dikkat edersek, (3) formülünden kaybolduğunu göreceğiz. Toplamın yerine ilk matriste ek boyutlar geldi. Doğrusal cebirin biraz daha eklenmesi, tüm formülü daha da temiz hâle getirecektir.

$$
f(\mathbf{X};\theta) = \mathbf{X}\theta $$

Arama işleminin sonuca varması için, hesaplanmış $f(x;\theta)$ ile verilen $\mathbf{y}$'i karşılaştırması gerekir. Bu karşılaştırmayı matematiksel olarak yapmanın karşılığı bir kayıp fonksiyonu (loss function) tanımlamaktır. Bu fonksiyon, başarı/başarısızlık kriterimizi tanımladığımız yer olacaktır. Diyelim ki kayıp kriteri (yâni bizim o an elimizde olan en iyi tahminin ne kadar yanlış olduğu) $f(x;\theta)$ işlevinin sonucu ile, veri olarak elimizde olan $\mathbf{y}$'nin farkının karesi olsun. Bu kayıp fonksiyonunu baz alarak, tüm noktalar için bu hesabı yapıp sonucu toplarsak, tüm riski hesaplamış oluruz.

$$ R(\theta) = \frac{1}{2N}|\mathbf{y} - \mathbf{X}\theta|^2 $$

Not: $2$ teriminin kullanılma sebebi, cebirsel işlemlerin ileri safhalarında $^2$ ile otomatikman iptal olması içindir. Risk fonksiyonunu herhangi bir sayı ile çarpmak, en alt (minima) noktasının nerede olduğunu değiştirmez.

Yapay öğrenim literatüründe $R(\theta)$ fonksiyonu ölçümsel risk olarak bilinir. Bizim amacımız R'yi minimize etmektir, ve bu şekilde, ve aynı zamanda, en iyi $\theta$'yı aramaktır. Altta 3 boyutlu risk fonksiyonu grafigi.

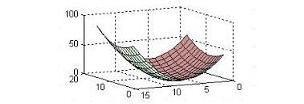
Risk'in en az olduğu nokta, fonksiyon değişimin en az olduğu noktadır, bunu analiz dersinden biliyoruz. Bu demektir ki, bu noktada $R(\theta)$'nin gradyan sıfır olacaktır. Gradyan, $R(\theta)$'nın bütün parça türevlerini (partial derivatives) vektör halindeki şeklidir. Bir işlevin gradyanını almanın sonucu elimize geçen vektör, her zaman o fonksiyonun, o noktadan hareketle en yüksek değişimin/artışın/azalışın olacağı yönü gösterecektir. Eğer bu gradyan sıfır olmuş ise, demek ki bir tam yatay düzleme geldik, ve hiç artış ve azalış imkanı kalmamış.

Bazı çeşit risk formüllerinin türevi cebirsel olarak çözülmesi zor bir sonuç verebilir. Bu gibi durumlarda, yaklaşıksal (approximate) tekniklerden birini kullanarak hesaplamayı yapabiliriz: Bir bilgisayar programı ile gradyanın işaret ettiği yöne doğru yürüyen bir yöntem takip ederiz. Bu sayede gradyanın sıfır olduğu bölgeye erişmeye uğraşırız. Program gradyan = 0 gördüğü anda duracaktır. Önümüzdeki örnek için çıkardığımız türev, cebirsel olarak temiz olacak, o yüzden yaklaşıksal, algoritmik tekniklere şimdilik ihtiyacımız yok.

$$ \bigtriangledown_{\theta} R\left(\theta\right) = \left[ \begin{array}{c} 0 \\ 0 \end{array} \right] $$

$$ \bigtriangledown_{\theta}\left( \frac{1}{2N}||\mathbf{y} - \mathbf{X}\theta||^2\right) = 0 $$

$$ \frac{1}{2N} \bigtriangledown_{\theta} \left( \left(\mathbf{y} - \mathbf{X}\theta \right) ^T \left( \mathbf{y} - \mathbf{X}\theta \right) \right) = 0 $$

$$ \frac{1}{2N} \bigtriangledown_{\theta} \left( \left(\mathbf{y}^T - \left(\mathbf{X}\theta\right)^T \right) \left( \mathbf{y} - \mathbf{X}\theta \right) \right) = 0 $$

$$ \frac{1}{2N} \bigtriangledown_{\theta} \left( \mathbf{y}^T\mathbf{y} - \mathbf{y}^T\mathbf{X}\theta - \left( \mathbf{X}\theta \right)^T\mathbf{y} + \theta^T\mathbf{X}^T\mathbf{X}\theta \right) = 0 $$

İkinci ve üçüncü terimler aslında birbirine eşittir, çünkü vektör çarpım kurallarına göre, $\mathbf{u}^T \mathbf{v} = \mathbf{v}^T \mathbf{u}$.

$$ \frac{1}{2N} \bigtriangledown_{\theta} \left( \mathbf{y}^T\mathbf{y} -2 \mathbf{y}^T\mathbf{X}\theta + \theta^T\mathbf{X}^T\mathbf{X}\theta \right) = 0 $$

$$ \frac{1}{2N} \left( -2\mathbf{y}^T\mathbf{X} +2\theta\mathbf{X}^T\mathbf{X} \right) = 0 $$

$$ \frac{1}{N} \left( -\mathbf{y}^T\mathbf{X} +\theta\mathbf{X}^T\mathbf{X} \right) = 0 $$

$$ \theta\mathbf{X}^T\mathbf{X} = \mathbf{y}^T\mathbf{X} $$

$$ \theta = \left(\mathbf{X}^T\mathbf{X}\right)^{-1} \mathbf{y}^T\mathbf{X} $$

$\theta$ hesaplandıktan sonra, artık bu değeri $f(x;\theta)$ içine koyabilir ve gelecekte bilinmeyen verileri tahmin için kullanabiliriz.

Yüksek Boyutlar

Doğrusal regresyon rahat bir şekilde çok boyutlu çalışacak şekilde uzatılabilir.

$$ \mathbf{X} = \left[ \begin{array}{cccc} 1 & x_{1} & \cdots & x_{1}(D) \\ \vdots & \vdots & \vdots & \vdots \\ 1 & x_{N} & \cdots & x_{N}(D) \\ \end{array} \right] \qquad (7) $$

$$ R\left(\theta\right) = \frac{1}{2N} \left| \left[ \begin{array}{c} y_{1} \\ \vdots \\ y_{N} \end{array} \right] - \mathbf{X} \left[ \begin{array}{c} \theta_{0} \\ \theta_{1} \\ \vdots \\ \theta_{D} \end{array} \right] \right|^2 $$

Yeni risk hesabı, N veri değeri ve D boyutu için kullanılabilir. $\theta$ hesabını ise gene aynen (7) denklemi üzerinden gerçekleştirebiliriz. Bu denklemden gelen sonuç, N boyutlu bir hiper düzlemin hâm veriye en uygun (fit) hâli olacaktır.

Baz Fonksiyonlar

Eğitim verisini modellemenin diğer bir yolu baz fonksiyonları olarak bilinen fonksiyonlardır. Bu yöntem ile, bir polinom, sinüsyen (sinüs bazlı) ya da radyal bir baz fonksiyon seçilir, ve her veri noktası $\mathbf{x}_{i\in N}$, baz fonksiyonundan geçirtilerek yeni bir $\mathbf{x}$ oluşturulur. Bu noktadan sonra uygulanacak regresyon işlemi, N baz fonksiyonunun en optimal hâldeki toplamının bulunma işlemine dönüşecektir. Baz fonksiyonları arasında en popüler olan radyal fonksiyonlardır, çünkü çok boyutlu veriyi modellememize izin verirler. Karşılaştırma olarak polinom bazlı fonksiyonlarda tek boyutun üzerine çıkamayız.

Bir radyal baz fonksiyonu hesaplamak, bir bakıma her nokta yerine bir tepe fonksiyonu yerleştirmektir. Bu tepe şöyle gösterilir:

$$ \phi_{i}(\mathbf{x}) = exp\left( -\frac{1}{2\sigma}\left|\mathbf{x} - \mathbf{x}_{i}\right|^2 \right) $$

ki $\mathbf{x}$ bir ya da çok boyutlu olabilir. Tepenin genişliği $\sigma$ parametresi ile kontrol edilir, ve regresyon işlemi başlamadan modelci tarafından seçilen bir değerdir. Bundan sonra risk fonksiyonu şu hâle gelecektir.

$$ R(\theta) = \frac{1}{2N}|\mathbf{y} - Q\theta|^2 $$

ki Q değeri şuna eşittir:

$$ \left[ \begin{array}{cccc} 1 & \phi_{0}(x_{1}) & \cdots & \phi_{D}(x_{1}) \\ \vdots & \vdots & \vdots & \vdots \\ 1 & \phi_{0}(x_{N}) & \cdots & \phi_{D}(x_{N}) \\ \end{array} \right] $$

Ve hâla (7) denklemini regresyon için kullanabiliriz.

Yapay Sinir Ağları

Düzeltici fonksiyonların eklenmesi ile regresyon biraz daha işe yarar hâle gelir. Bunun da üstüne, regresyonu değişik seviyelerde birkaç kez yapar ve her seviyede değişik düzeltici (ya da aynı) düzeltici fonksiyonlar kullanırsak, Alttaki sekilde gördüğümüz daha çetrefilli ayrıcı problemleri çözmemiz mümkün olacaktır. Bu tür yaklaşımlara ağa benzer yapısı sebebiyle yapay sinir ağları (neural network) adı verilmiştir.

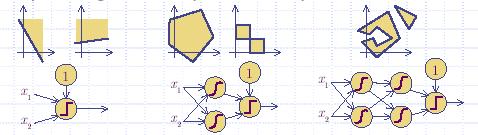
Düzeltici fonksiyonların ağ yapısına eklenmesiyle birlikte, gradyan yöntemini kullanarak pür cebirsel olarak en alt noktayı bulmak zorlaşır. Bu yüzden yaklaşıksal yöntemler kullanmaya mecbur oluyoruz. Bu yöntemlerden biri gradyan inişi (gradient descent) adı verilen bir yöntemdir. Çok katmanlı bir yapay sinir ağ için gradyan inişi her katmana sırayla uygulanır, ki YSA eğitmekte kullanılan ünlü BACKPROP algoritmasının altında yatan temel fikir budur. BACKPROP birçok uygulama alanında başarı ile kullanılmıştır.

Bu ek gücüne rağmen, YSA'nın bazı limitasyonları hâlen mevcuttur. Öncelikle YSA'ların matematiksel analizi hala zordur. Ağ yapısına yeni bir katman eklediğimizde bunun sonuçlarının ne olacağını hâlen bilmiyoruz. Ayrıca analiz bir tarafa, YSA ile çözülmesi mümkün olmayan problemler de mevcuttur. Meselâ $x^2+y^2=1$ formülünü öğrenmek bunlardan biridir çünkü, bu formül bir fonksiyon değil, bir ilişkidir. Diğer bir ünlü problem balistikten Gülle Atmanın Açısı ve Uzaklığı problemidir ve regresyon bazlı bir yöntem kullanarak çözmek imkansızdır. Bu tür problemler en rahat şekilde Bayes Ağları gibi bir istatistiki yaklaşım ile çözülebilir.

İstatistiki Yaklaşım

İstatistiki yaklaşım, veriyi daha iyi ve kesin özetleyebilmemizi sağlar. İki boyutlu bir veri için regresyon yapınca, bilinmeyen bir doğrunun sadece açısını öğrenmiş oluyoruz. İstatistiki yaklaşım ile bir Gauss Normal dağılımın parametrelerini veriden çıkartınca, elimize geçenler merkez nokta $\mu$ (ortalama), dağılımın genişliği $\sigma$ (varyans), ve elipsin açısı $\Sigma$ (kovaryans) olacaktır. İstatistiki yaklaşım, aynı zamanda, olasılık kuramının bütün araçlarını kullanmamıza imkan verdiği için, altyapı daha sağlam olacaktır, ve böylece rasgele yöntemlere daha az başvurmuş olacağız, ve ileride modeli analiz etmemiz kolaylaşacak.

Olasılık modellerinde, tek bir parametreyi öğrenmek yerine, o parametrenin üstünden tanımlanan bir dağılımı öğreniyoruz. Yâni $y$ yerine $p(y)$ kullanıyoruz. Diğer taraftan, eski yöntemde $p(y)$ yerine $y$ kullanmak, bütün ağırlığı tek bir noktada toplanmış bir dağılım öğrenmek ile aynı şey oluyor.

Bir dağılıma birden fazla bilinmeyen eklemenin sonucu elimize bir ortak dağılım (joint distribution) geçmesidir. Ayrıksal (discrete) şartlarda ortak dağılım bir tablo olarak gösterilebilir ve belli (sonlu) sayıda elemanı vardır.

Rasgele (random) değişkenler arasındaki bağımlılık ve bağımsızlık da ortak dağılım tablo büyüklüğünde etkileyici bir faktördür. Eğer iki olayın, ve bu sebeple bu olayların rasgele değişkenlerinin arasında bir ilişki var ise, modelimizin bu ilişkiyi yansıtması isabetli olacaktır. Fakat basitleştirmek için (meselâ) bütün değişkenlerin arasında bir ilişki kuracak olsaydık, bunun sonucu tablomuzun büyüklüğünde üstel bir patlama olurdu. Örnek olarak D bilinmeyenli ve hepsi birbiri ile ilişkili rasgele değişkenler üstünden bir dağılımın tablo büyüklüğü $2^D$ iken, bütün rasgele değişkenler birbirinden bağımsız olduğu durumda ise büyüklük $2D$'a inecektir.

Bu yüzden verimli bir yöntem şöyle olabilir: $2D$, yâni tam bağımsızlık ile başlarız ve bağımlılık ilişkisini yavaş yavaş modele tanıştırırız. Değişkenler arasındaki bağımlılık ilişkisi $p(y|x)$ olarak gösterilir, ve okunuşu"x verildiğinde $y$'nin olasılığı" olarak tanımlanır. Ortak dağılım $p(x,y) = p(y|x)p(x)$ olarak bilinir ve bu eşitlik olasılık kuramından iyi bilinen bir eşitliktir. Çok bilinmeyen içeren bir problemde bütün bağımlılıkların formül olarak yazılması karışık olabileceğinden, genelde çizit notasyonu kullanılır. Alttaki sekilde görülen ortak dağılım $p(x,y,z)$, bütün olasılıkların çarpımına eşittir, yâni $p(x)p(y|x)p(z|x)$.

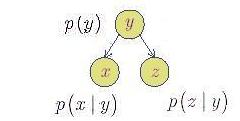
Dikkat edilirse, bu modele göre $p(x,y,z)$ ortak dağılımı $p(x)p(y)p(z)$ çarpımına eşit değildir. Bu sonuç sadece ve sadece bütün değişkenler birbirinden bağımsız ise ortaya çıkacaktır.

Olasılık dağılımlarını kullanırken, modelin bilinmeyenlerini, yâni parametrelerini bile bir rasgele değişken olarak gösterilebilir. Böylece diğer rasgele değişkenler ile bu tür değişkenler arasında bağımlılık ilişkisi kurulabilir. Meselâ, alttaki sekildeki noktaları sınıflandırma örneğinden başlayalım.

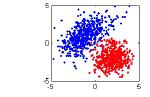
Bu örnekte, $x \in \mathbf{R}^D$ girdi verisidir, ve $y \in {0,1}$ de sonuçtur. Değişken y ikili sistemde olduğu için, bu dağılımı bir Bernoulli Dağılımı olarak modelleyebiliriz.

$$ p(y_{i}|\alpha)=\alpha^y_{i}(1-\alpha)^{1-y_{i}} $$

ki $i=1...N$. Bir dağılım tablosu yerine dağılım formülü kullanmak bize dağılımı cebirsel olarak manipüle etme avantajını sağlar. Bu sayede formülü En Büyük Olurluk (Maximum Likelihood) gibi bir metoda girdi olarak verebiliriz, formülün türevini alabiliriz, vs.

X'leri temsil etmek için Gaussian dağılımını seçeceğiz.

$$ p(x_{i}|y_{i},\mu,\Sigma)=N(x_{i}|\mu_{y},\Sigma_{y})
\qquad (11) $$

Ortak dağılım da alttaki gibi gözükecektir.

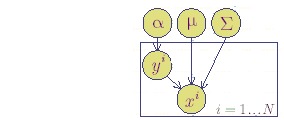
Gördüğümüz gibi $\mu,\alpha,\Sigma$ değişkenleri de rasgele değişkeni hâline getirildi. Grafiğe bakarak cebirsel ortak dağılımı $p(x,y,\mu,\alpha,\Sigma)$ şöyle gösterebiliriz.

$$ p(y|\alpha)p(x|y,\mu,\Sigma)p(\Sigma)p(\mu)p(\alpha) \qquad (12) $$

Sınıflandırma amacımıza erişebilmek için (12) formülünü, $p(x,y|\alpha,\mu,\Sigma)$ sorusunu cevaplandırabilen bir hâle getirmeliyiz. Olasılık kuramından bilinen bir değişim ile pür cebirsel olarak şöyle devam edebiliriz.

$$ p(x,y|\alpha,\mu,\Sigma) = \frac{p(x,y,\alpha,\mu,\Sigma)} {p(\alpha)p(\mu)p(\Sigma)} \qquad (13) $$

Şimdi (13)'deki bölüneni, grafik modelden gelen ortak dağılım (12) ile değiştireceğiz.

$$ p(x,y|\alpha,\mu,\Sigma) = \frac{p(y|x)p(x|y,\mu,\Sigma)p(\alpha)p(\mu)p(\Sigma)} {p(\alpha)p(\mu)p(\Sigma)} \nonumber \\ = p(y|x)p(x|y,\mu,\Sigma) \qquad (14) $$

Eğitim (hâm) verisine en uygun olan parametreleri bulmak için, En Büyük Olurluk yöntemini kullanacağız. Bu metoda göre (14) formülünün her N veri noktası ile hesabından sonra birbiri ile çarparız. O zaman, bilinmeyen parametrelerin en iyi hesapsal tahmini (estimation), bu süper ortak dağılımın en yüksek olduğu noktada bulunabilir.

$$ Olurluk = \prod_{i=1}^N p(y|x)p(x|y,\mu,\Sigma) \qquad (15) $$

Olurluğun en yüksek olduğu nokta, olurluk formülünün türevinin sıfır olduğu noktadadır.

İleride yapılacak türev alma işlemini rahatlatmak için, (15) içindeki terimlerin log'unu alırız. Bu işlem, çarpım işaretini toplam işaretine dönüştürecektir. Bunu yapmamız en yüksek noktayı bulma açısından bir fark yaratmaz, çünkü (15) formülünün değişim hızı, toplamlı olan formülünkiyle aynıdır.

$$ l = \sum_{i=1}^N \log (p(y_{i}|x_{i})) + \sum_{i=1}^N \log (p(x_{i}|y_{i},\mu,\Sigma)) $$

Son terimi iki toplama çevirebiliriz. Bunun için $y$ üzerinden özetlemeyi (marginalize) iki parça halinde, $y$'nin mümkün her değeri için yapacağız.

$$ l = \sum_{i=1}^N \log(p(y_{i}|\alpha)) + \sum_{y_{i}\in 0} \log(p(x_{i}|\mu_{0},\Sigma_{0})) + \sum_{y_{i}\in 1} \log(p(x_{i}|\mu_{1},\Sigma_{1})) \qquad (16) $$

Şimdi, olurluğun gradyanını $\alpha, \Sigma, \mu$'a göre (ayrı ayrı) alırsak ve bu sonuç formülleri sıfıra eşitleyip çözersek, elimize geçen parametre değerleri veriyi açıklayan en mümkün parametre değerleri olacaktır. Örnek olarak $\frac{\partial l}{\partial \alpha}$ gradyanını alalım. Parçalı türevi $\alpha$'ya göre aldığımız için, birincisi hariç (16) içindeki bütün terimler yokolur. Sonuç olarak şu olur:

$$ \frac{\partial l}{\partial \alpha} = \frac{\partial }{\partial \alpha} \sum_{i=1}^N \log (p(y_{i}|\alpha)) $$

$$ 0 = \frac{\partial}{\partial \alpha} \sum_{i=1}^N \log\left(\alpha^y_{i}(1-\alpha)^{1-y_{i}}\right) $$

$$
0 = \frac{\partial}{\partial \alpha} \sum_{i=1}^N y_{i}\log(\alpha) + (1-y_{i})\log(1-\alpha) $$

Problem alanından bildiğimiz üzere, bazı $y_{i}$'ler 0 olacak, bazılari ise 1. Sıfır değerler $y_{i}\log(\alpha)$'yi iptal edecektir, bir değerleri de $(1-y_{i})\log(1-\alpha)$'i iptal edecektir. O zaman, $y_{i}$'leri formülden yoketmek için tüm formülü şöyle değiştirebiliriz.

$$ 0 = \frac{\partial}{\partial \alpha}\ \left( \sum_{i\in class1} \log(\alpha) + \sum_{i\in class0} \log(1-\alpha) \right) $$

$$ 0 = \sum_{i\in class1}\frac{1}{\alpha} - \sum_{i\in class0}\frac{1}{1-\alpha} $$

Eğer $N_{0}$ değişkenini 0 sınıfında olan i'ların toplamı, $N_{1}$'i 1 sınıfında olan i'ların sayısı olarak alırsak

$$ 0 = \frac{N_{1}}{\alpha}-\frac{N_{0}}{1-\alpha} $$

$$ \alpha = \frac{N_{1}}{N_{1}+N_{0}} = \frac{N_{1}}{N} $$

olur. Bu sonuç, $y_{i}=1$ olan $y_{i}$'leri, toplam veri noktası sayısına bölünce $\alpha$'nın bulunabileceği şeklindeki önseziyi de desteklemiş oluyor. Bunu tahmin de edebilirdik, ama bu önsezinin En Büyük Olurluk yöntemi tarafından matematiksel olarak doğrulanmış olması daha rahatlatıcı oldu.

Diğer bilinmeyenler $\mu_{0}, \mu_{1}, \Sigma_{0}, \Sigma_{1}$ için benzer yöntemi takip edebiliriz. (16)'in türevini bilinmeyen rasgelen değişkene göre alırız, sıfıra eşitleriz ve çözeririz. Bu işlem yer darlığı sebebiyle burada gösterilmeyecektir. Bu işlemlerin sonunda formül (11)'deki tüm bilinmeyenleri bulabiliriz. (11)'i daha önce bulunmuş olan $p(y)$ ile kullanınca, (14)'u nihayet sınıflama için kullanmamız mümkün olacaktır. Yapay Öğrenim literatüründe $p(y)$, ilk tahmin (prior guess) olarak da bilinir.

Sınıflama

Sınıflama için bir formül daha türetmemiz gerekiyor: $p(y|x)$. Bu formül, sonraki tahmin (posterior) olarak bilinir, ve bilindikten sonra bize verilen ve sınıflandırılmamış yeni veri $x$'i $p(y|x=yeni deger)$ şeklinde bu formülden geçiririz, ve $y$'nin olurluğunu hesaplarız.

Şimdi sonraki tahmin, $p(y|x)$'i türetelim. Olasılık kuramından,

$$ p(y|x) = \frac{p(x,y)}{p(x)} $$

Bunun işlemesi için $p(x)$'e ihtiyacımız var. $p(x,y)$'i alalım, ve $y$ üzerinden özetleyelim.

$$ p(y|x) = \frac{p(x,y)}{\sum_{y}p(x,y)}
$$

$$
= \frac{p(x,y)}{p(x,y=0) + p(x,y=1)} $$

Artık sınıflama işlemi, $p(y=1|x)$ ve $p(y=0|x)$ formüllerini ayrı ayrı hesaplamaktan ibarettir. Hangi olasılık daha büyük ise, o y değeri $x$'in ait olduğu sınıf olacaktır.

Kaynaklar

[1] C. Bishop Neural Networks for Pattern Recognition, Oxford University Press, 1995.

[2] R. O. Duda, P. E. Hart \& D. G. Stork Pattern Classification (2nd ed), Wiley, 2000.

[3] M. Jordan, C. Bishop, Introduction to Graphical Models (Online), not yet published.

[4] T. Mitchell, Machine Learning, McGraw-Hill, 1997.