Otomatik oyun oynayan yapay zeka öğreten derslerdeki kilometre taşlarından biri altüst / minimaks algoritmasiydi. Notlarımızda anlattığımız bu algoritma, bir oyunda bizim yaptığımız, rakibin yaptığı tüm hamle seçeneklerine göre oluşan tahta konfigürasyonlarına bakarak ve bu tahtalara değer atayabilen bir değer fonksiyonuyla onları irdeleyerek rakip için en kötü bizim için en iyi olacak şekilde bir arama ile optimal oyun hamlelerini buluyordu.
Fakat minimaksın bir problemi şudur: birkaç hamle sonrasına bakmak için tüm mümkün hamlelere göre kurulan ağaç müthiş büyük olabilir. Özellikle Go oyunu [1] gibi dallanma faktörü çok büyük olan oyunlarda minimaks zorluk yaşayabiliyor. Bu gibi durumlarda MCTS yaklaşımının daha başarılı olduğu bulunmuştur.
Şimdi MCTS’i anlatalım, özelde UCT adı verilen üst güven aralığının ağaçlara uygulanması (upper-confidence applied to trees) adlı çeşidini gösterelim. Bunun için tabii önce UCT’yi ve onun baz çeşidi UCB1’i anlamak lazım.
Kumarhanelerdeki o kollu oyun makinalarını düşünelim, oyuncunun önünde bunlardan birkaç tane olsun, ve bu makinalardan her birinin farklı ve bilinmeyen bir getiri dağılımı var. Tek kollu makinalara argoda “tek kollu soyguncu (one-armed bandit)’’ de denilir, bilgisayarcılar üstteki üstteki probleme”çok kollu soyguncu (multi-armed bandit)’’ ismi veriyorlar. Biraz esprili bir şekilde bu makinaları çok kollu bir ahtapotun hayal ediliyor bazen, ki ahtapot akıllı, yani oyunu optimal oynayacak bilgisayar programı.

Aklımızdaki soru şu; Getirisi en iyi olacak makina acaba hangisi? Bilsek hemen onu oynardık. Bunu başta bilmiyoruz, oturup başkasını seyredecek durumda değiliz, o zaman hem seçenekleri bir şekilde deneyecek ama bu sırada çok getiri kaybı yaşamayacak aynı zamanda uzun vadede kazançta kalacak şekilde bu oyunu oynamak istiyoruz. UCB1 adlı bir strateji bunu yapabiliyor, bu stratejiye göre her makina \(i\) için bir istatistiki güven aralığı yaratılır,
\[ \overline{x}_i \pm \sqrt{\frac{2 \ln n}{n_i}} \]
\(\overline{x}_i\): Makine \(i\)’nin ortalama getirisi
\(n_i\): Makine \(i\)’nin kaç kere oynandığı
\(n\): Tüm oyunlar (tüm makinelerde kaç kere oynandığı)
Ve stratejimiz her adımda üst sınırı en yüksek olan makinayı oynamaktır. Bunu yaptıkça o makinanın gözlenen ortalaması kazanca / kayıba göre kayacak, ve güven aralığı ufalacak (elimizde daha fazla veri var çünkü, daha fazla veri daha fazla kesinlik demek), ve diğer makinaların aralığı genişleyecek. Bir noktada başka bir makinanın üst sınırı o anda oynadığımızı geçecek, o zaman biz bu öteki makinaya geçeceğiz. Uzun vadede bu strateji optimal olarak sonuç vermektedir.
Türetmek için notasyonu biraz değiştirelim [3], \(a\) bir aksiyon (ya da makina seçimi), \(Q(a) = E(r|a)\), bir aksiyon için ortalama getiri, \(U_t(a)\) adım \(t\)’de bir aksiyonun üst sınırı, \(\hat{Q}, \hat{U}\) kestirme değerler, \(N(a)\) bir aksiyonun kaç kez seçildiği. Hem \(\hat{U}\) kestirme değerini sürekli hesaplayacağız, hem de güven aralığını maksimize eden aksiyonu seçeceğiz, yani.
\[ a_t = \arg \max_{a \in A} \hat{Q}_t(a) + \hat{U}_t(a) \]
Bu seçimi yaparken yüksek olasılıkla (with high probability) \(Q(a) \le \hat{Q}_t(a) + \hat{U}_t(a)\) olmasını sağlayacağız. Bu şart için Hoeffding eşitsizliğinden başlayabiliriz (bkz [5]).
\(X_1,...X_n\) \([0,1]\) aralığında bağımsız özdeşçe dağılmış (i.i.d.) değerlere sahip rasgele değişkenler olsunlar, ve \(\overline{X}_t = \frac{1}{\tau} \sum_{\tau=1}^{t} X_\tau\) örneklem ortalaması olsun. O zaman
\[ P(E(X) > \overline{X}_t + u ) \le e^{-2 t u^2}\]
olduğunu biliyoruz, soyguncu problemindeki getiri rasgele değişkenleri için uyarlarsak,
\[ P \big( Q(a) > \hat{Q}_t(a) + U_t(a) \big) \le e^{-2 N_t(a)U_t(a)^2 } \]
İstediğimiz şartların oluşması için üstteki formülün doğruluğu yeterli, şimdi bu formülü baz alarak bir \(U_t(a)\) hesaplayabiliriz, formülü \(U_t(a)\) tek başına kalacak şekilde tekrar düzenleyebiliriz. Eşitliğin sol tarafına \(p\) diyelim, burada sanki istenilen bir güven aralık büyüklüğünü baz almış oluyoruz, 95% (yani 0.95) gibi, ama burada sembolik bir değer kulladık, ilk amacımız \(u\) değerine erişmek,
\[ e^{-2 N_t(a)U_t(a)^2 } = p \]
\[ \ln p = -2 N_t(a)U_t(a)^2 \]
\[ \frac{-\ln p}{2 N_t(a)} = U_t(a)^2 \]
\[ U_t(a) = \sqrt{\frac{-\ln p}{2 N_t(a)}} \]
\(t\) büyüdükçe \(p\) azalsın istiyoruz, o zaman \(p = t^{-4}\) seçebiliriz, bu spesifik değer formülü de basitleştirmek için seçildi bir yandan,
\[ U_t(a) = \sqrt{\frac{\log t}{N_t(a)}} \]
Böylece UCB1 algoritmasına erişmiş olduk,
\[ a_t = \arg \max_{a \in A} Q(a) + \sqrt{\frac{\log t}{N_t(a)}} \]
UCT ve Tic-Tac-Toe
Oyunlar ve Monte Carlo işin için nasıl dahil oluyor? Mesela her adımda bir sonraki en iyi adımı bulmak istiyoruz, MC ile bu geçişi simüle ederiz, yani rasgele tahta hamlelerini deneyerek iyi olan bitişleri bulmaya uğraşırız. Bu yöntemin bir kötü tarafı, minimaks durumunda olduğu gibi, çok fazla hamle seçeneği olduğu zaman ortaya çıkar, rasgele seçim de, tüm seçenekleri deneyen deterministik seçim gibi yetersiz kalabilir.
UCT burada bir çözüm olarak görülebilir. Fikir şu: verili bir tahta konumundan atılacak bir adım ötesi bir çok-kollu soyguncu problemi olarak görülebilir.
İlk faz seçim fazıdır, başlangıç konumundan aşağı inmeye başlarız, ve eğer baktığımız tüm düğümlerde çok-kollu soyguncu seçimi için gerekli istatistikler var ise seçim UCB1 ile yapılır, ve devam edilir. Bu ta ki üzerinde istatistik olmayan (yani hiç ziyaret edilmemiş) bir düğüme gelinceye kadar devam eder. Eğer böyle bir düğüm(ler) var ise onlar arasından rasgele seçim yapılır, böylece o düğüm ve altındakiler ziyaret edilmiş olur ve kayıp / kazanç sonrası onların da artık istatistikleri olur ve bir sonraki adımda onlar da UCB1 ile seçiliyor (ya da seçilmiyor) olacaktır.
Örnek olarak bir Tic-Tac-Toe oyunu için bir örnek görelim. X ve O taşları var, biz O için hesap yapıyoruz diyelim. A pozisyonunda (en üst) tüm alt pozisyonlar hakkında istatistik var. Mesela 1/2 görüyoruz, bu o pozisyondan iki kere geçilmiş bu geçişlerden birisi oyunun kazanılması ile bitmiş (bu bir kazanç en sol alttaki bitiş). Şimdi bir A’dan bir kez daha geliyoruz, UCB1 bize pozisyon B’ye git diyor, o seviyede en sağdaki düğüm için hiç bilgi yok, o zaman rasgele olarak o seçiliyor, oradan tek seçenek var, ve O kazanıyor. Böylece B pozisyonundaki istatistik 2/3 haline geliyor. Başlangıçtan oyun bitişine kadar her gidiş simulasyonda bir döngü, eğer 100 kere simüle et dersek bu döngü 100 kere döner.
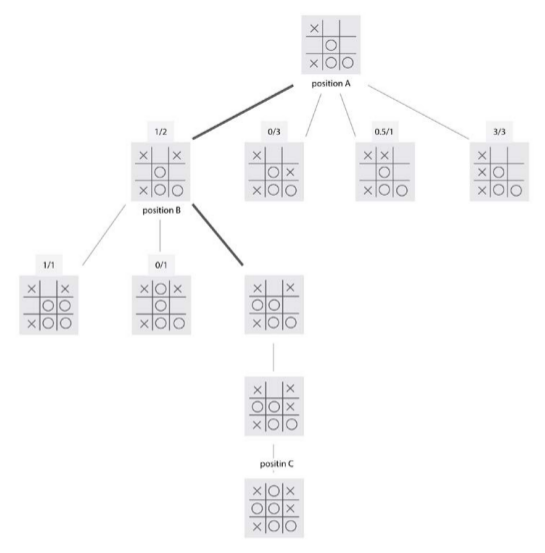
Kod üzerinde görelim, üstteki başlangıç pozisyonundan X için (oyuncu 1, öteki oyuncu -1) simulasyon yapalım, 1000 kere,
import collections
import random
import math
import random
import itertools
import pandas as pd
import numpy as np
def _new_board():
return ((0, 0, 0),
(0, 0, 0),
(0, 0, 0))
def apply_move(board_state, move, side):
move_x, move_y = move
def get_tuples():
for x in range(3):
if move_x == x:
temp = list(board_state[x])
temp[move_y] = side
yield tuple(temp)
else:
yield board_state[x]
return tuple(get_tuples())
def available_moves(board_state):
for x, y in itertools.product(range(3), range(3)):
if board_state[x][y] == 0:
yield (x, y)
def _has_3_in_a_line(line):
return all(x == -1 for x in line) | all(x == 1 for x in line)
def has_winner(board_state):
# check rows
for x in range(3):
if _has_3_in_a_line(board_state[x]):
return board_state[x][0]
# check columns
for y in range(3):
if _has_3_in_a_line([i[y] for i in board_state]):
return board_state[0][y]
# check diagonals
if _has_3_in_a_line([board_state[i][i] for i in range(3)]):
return board_state[0][0]
if _has_3_in_a_line([board_state[2 - i][i] for i in range(3)]):
return board_state[0][2]
return 0 # no one has won, return 0 for a draw
def _upper_confidence_bounds(payout, samples_for_this_machine, log_total_samples):
return payout / samples_for_this_machine + \
math.sqrt((2 * log_total_samples) / samples_for_this_machine)
def monte_carlo_tree_search_uct(board_state, side, number_of_samples):
state_results = collections.defaultdict(float)
state_samples = collections.defaultdict(float)
for _ in range(number_of_samples):
current_side = side
current_board_state = board_state
first_unvisited_node = True
rollout_path = []
result = 0
while result == 0:
move_states = {move: apply_move(current_board_state, move, current_side)
for move in available_moves(current_board_state)}
if not move_states:
result = 0
break
if all((state in state_samples) for _, state in move_states):
log_total_samples = math.log(sum(state_samples[s] \
for s in move_states.values()))
l = lambda _, s: _upper_confidence_bounds(state_results[s],
state_samples[s],
log_total_samples)
move, state = max(move_states, key=l)
else:
move = random.choice(list(move_states.keys()))
current_board_state = move_states[move]
if first_unvisited_node:
rollout_path.append((current_board_state, current_side))
if current_board_state not in state_samples:
first_unvisited_node = False
current_side = -current_side
result = has_winner(current_board_state)
for path_board_state, path_side in rollout_path:
state_samples[path_board_state] += 1.
result *= path_side
result /= 2.
result += .5
state_results[path_board_state] += result
move_states = {move: apply_move(board_state, move, side) \
for move in available_moves(board_state)}
l2 = lambda x: state_results[move_states[x]] / state_samples[move_states[x]]
move = max(move_states, key=l2)
return state_results[move_states[move]] / state_samples[move_states[move]], move
import tictac_uct
board_state = ((1, 0, 0),
(0, -1, 0),
(1, -1, -1))
res, move = tictac_uct.monte_carlo_tree_search_uct(board_state, 1, 1000)
print move(1, 0)X taşını üstten 2. satır ve 1. kolona koymamız isteniyor (Python 0 indisli hatırlarsak), bu hareketi yapıyoruz,
b = np.array(board_state)
b[move] = 1.0
print bVe bu kazanan hareket, resimde ikinci seviyede en sağdaki hamle oluyor. UCB1 doğru tavsiyeyi vermiş gibi duruyor.
Not: MCTS algoritmasinin bol kullanım alanı var, A/B testlerinin istatistiksel hesabı yerine MCTS kullanmak mümkün, yani iki sayfa versiyonu arasında hangisinin daha iyi olduğu da bir tür çok-kollu soyguncu problemi olarak görülebiliyor.
Kaynaklar
[1] Bayramlı, Go Oyunu, GnuGo, https://burakbayramli.github.io/dersblog/sk/2018/02/go-gnugo.html
[2] Bradberry, Introduction to Monte Carlo Tree Search, https://jeffbradberry.com/posts/2015/09/intro-to-monte-carlo-tree-search
[3] Silver, Reinforcement Learning, http://www0.cs.ucl.ac.uk/staff/d.silver/web/Teaching.html
[4] Zocca, Python Deep Learning
[5] Bayramlı, İstatistik, Ekler