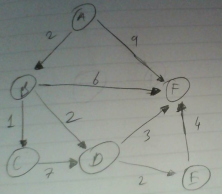
Dinamik programlamanın (DP) temelinde ardı ardına verilen kararların bulunması / hesaplanması fikri vardır; ilgilendiği problemler her verilen kararın diğer karar seçeneklerini ortaya çıkardığı türden problemlerdir, ve her seferinde bu seçeneklerin arasından bir tanesi seçilmelidir. Amaç en iyi karar zincirini bulmaktır. Metot olarak kullanılanlar kısmen “açgözlü algoritmalar (greedy algorithms)’’ olarak bilinen algoritmaların yaptığına benzer fakat açgözlü algoritmalar en kısa yolu bulmaya uğraşırken, gezilen düğümlerde sadece”o an için’’ en iyi seçimi yapar. Bu tür seçim nihai sonuç göze alındığı zamanen iyi sonucu vermeyebilir. Alttaki grafiğe bakarsak,

diyelim ki a noktasından f noktasına en
kısa yoldan ulaşmaya çalışıyoruz - açgözlü algoritma
a,b,c,d üzerinden gidiş yapardı çünkü her an, sadece o an
için en iyi olanı seçerdi. Fakat en iyi yol a,b,d üzerinden
giden yoldur. Gösterilen çizit / ağ yapısı (graph) yönlü ve çevrimsiz
(directed, acyclic graph -DAG-) olarak bilinen bir yapı. Tipik kısa yol
problemleri bu yapılar üzerinde çalışırlar.
DP problemleri özellikle bir problemi alt problemlere bölebildiğimiz zaman faydalıdırlar, ve bu alt problemler tekrar tekrar hesaplanıyorlarsa da bu daha iyidir, çünkü DP o alt problemleri önbellekleyerek (caching) tekrar hesaplanmadan geri getirilmelerini sağlayabilir.
Üstteki en kısa yol problemini DP ile çözelim.
Önce bazı teorik, mantıksal konular: tümevarımsal olarak düşünelim. Diyelim ki üstteki DAG’de \(a,f\) arasındaki en kısa yolu kesinlikle “biliyoruz’’. Ve yine diyelim ki bu yol üzerinde / bir ara nokta \(x\) noktası var. O zaman, \(a,x\), ve \(x,f\) arasındaki yollar da tanım itibariyle en kısadır. İspatlayalım: eğer mesela \(x,f\) arasındaki en kısa yol bildiğimizden başka olsaydı, o zaman eldekini atıp o yolu kullanıyor olurduk (en kısa olduğunu kesin biliyoruz ya), ve bu sefer o alternatif en kısa olurdu. Fakat ilk başta en kısa yolu bildiğimiz faraziyesi ile başladık. Bir çelişki elde ettik, demek ki ara noktanın kısalığı doğrudur \(\square\)
Bu ispattan hareketle kısa yolu tek sayısal (numeric) bir değer olarak hesaplamaya uğraşabiliriz.
Öyle bir fonksiyon \(d(v)\) olsun ki herhangi bir \(v\) nodu için o nod’dan bitiş noktasına olan en kısa uzaklığı kesin biliyor olsun (dikkat, bu hesabın nasıl olacağını düşünmüyoruz şimdilik, sadece olabileceğini, olmuş olduğunu farz ediyoruz). Çoğu tümevarımsal tasarımda olduğu gibi hesabın kendisinin özyinelilik (recursive) çağrı zincirinin mekaniği içinde halolmasını amaçlıyoruz. Doğru olan bir ifadeyi düşünüyoruz öncelikle, ve hesabın kendisini sürekli bir sonraki noktaya erteliyoruz.
Devam edelim: \(u,v\) arasındaki parça mesafeler \(w(u,v)\)’dir. Şimdi, eğer bir ara nokta \(u\)’ya gelmişsek -yine tümevarımsal olarak düşünmeye devam ediyoruz- bu noktanın her komşusu \(w\) için \(d(w)\)’yi “bildiğimize’’ göre, en kısa yol için tek yapmamız gereken her seçim anında en minimal \(w(u,v) + d(v)\)’yi \(u\)’nun uzaklığı olarak almaktır.
Veri yapısı olarak DAG’ı alttaki gibi gösterelim,
DAG = {
'a': {'b':2, 'f': 9},
'b': {'d':2, 'c':1, 'f': 6},
'c': {'d':7},
'd': {'e':2, 'f': 3},
'e': {'f':4},
'f': {}
}Böylece \(w(u,v)\) basit bir Python
sözlük (dictionary) erişimi haline geliyor, a,b arası parça
mesafe için
print (DAG['a']['b'])2En kısa yolu bulacak program
from functools import wraps
def memo(func):
cache = {}
@wraps(func)
def wrap(*args):
if args not in cache:
print ('onbellekte yok -', args[0])
cache[args] = func(*args)
else: print ('onbellekte var -', args[0])
return cache[args]
return wrap from memo import *
def rec_dag_sp(W, s, t):
@memo
def d(u):
print ('Dugum:' + u[0])
if u == t: print ('Son nokta t, geri donus'); return 0
min_dist = min(W[u][v]+d(v) for v in W[u])
print ('Geri donus,',u,'uzerindeyiz, mesafe=',min_dist)
return min_dist
return d(s)
dist = rec_dag_sp(DAG, 'a', 'f')
print ('toplam mesafe=', dist)onbellekte yok - a
Dugum:a
onbellekte yok - b
Dugum:b
onbellekte yok - c
Dugum:c
onbellekte yok - d
Dugum:d
onbellekte yok - e
Dugum:e
onbellekte yok - f
Dugum:f
Son nokta t, geri donus
Geri donus, e uzerindeyiz, mesafe= 4
onbellekte var - f
Geri donus, d uzerindeyiz, mesafe= 3
Geri donus, c uzerindeyiz, mesafe= 10
onbellekte var - d
onbellekte var - f
Geri donus, b uzerindeyiz, mesafe= 5
onbellekte var - f
Geri donus, a uzerindeyiz, mesafe= 7
toplam mesafe= 7Şimdi çağrı mekaniğinin hakikaten nasıl işlediğini görelim. Not: Önbellek kodlaması dekoratör kullanıyor, dekoratörler hakkında bir yazı için [2].
Başlangıç \(u\), oradan, minimum seçerken, sürekli \(d()\) çağrısı yapıyoruz, yani \(d()\) kendini çağırıyor. Çağrının geri dönmesinin tek yolu son noktaya erişmek. Bu ne demektir? Programımız daha hesap yapmadan “derinliğine bir dalış’’ yapıyor. Son noktalara gelene kadar özyineli çağrıları ardı ardına uyguluyor, esas hesapları geri dönüş sırasında yapıyor. Bu nasıl ise yarıyor? Ayrıca önbelleklemenin hakikaten işleyip işlemediğini nasıl bileceğiz? Ya da önbellekteki bir değerin hep en iyisi olduğunu nereden bileceğim?
Bu arada, böyle bir yaklaşımda, önbellek değeri bir kez set edildi mi, hiç değiştirmeye gerek yok.
Nokta d‘ye bakalım. Bu noktanın mesafesi (yani son nokta
f’ye uzaklığı) kararlaştırılırken algoritma
d’nin her komşusuna bakacaktır, bunu
for v in W[u]) ile yapacaktır. Her komşu için
f’ye gelene kadar o yol derinliğine takıp edilecektir.
Üstteki çıktıda görüyoruz ki d sonrası iki komşu
e,f için önce d-f ve d-e-f gidişi
yapılmıştır (amaç hep o son noktaya ulaşmak, unutmayalım). ’Komşulara
bakma ve aralarından en azı seçme’’ mantığı tüm bu yollar denenene kadar
bekleyecektir, ancak hepsi bittikten sonra içlerinden bir minimum
seçecektir.
İşte şimdi niye her düğümdeki minimum hesabının en iyisi olduğunu
anlıyoruz, çünkü o noktadan nihai noktaya varış için tüm alternatifler
deneniyor. O derine dalışın sonuçları arasından bir tanesi seçiliyor.
önbellekteki değer bu sebeple bir kez set ediliyor, ve hiç değişmiyor.
Tabii ki önbellekteki değer tekrar tekrar kullanılabiliyor,
c için bir d uzaklığı gerektiğinde bu
önbellekten servis edilecektir.
Ve her düğümdeki minimum hesabı en iyiyse, bu hesapları kullanan başlangıca yakın noktaların hesabı da doğal olarak en iyisi (kısası) olacaktır. Başta tümevarımsal olarak belirttiğimizin tekrar ifade edilmesidir bu.
Kısa Yol Tarifini Bulmak
Mesafe hesabı işte böyle yapılıyor… Peki en kısa yolun kendisini
nasıl biliriz? Yani önce şuraya, sonra şuraya git türünden yol tarifi
bilgisi nasıl hesaplanır? Aslında komşular arasındaki en kısa mesafeyi
seçme problemi, o komşular içinden hangisinin o en mesafeyi sağladığını
hatırlama problemine oldukça benziyor. Yani, her düğüm üzerindeyken ve
komşular arasından en kısa mesafeyi seçerken, o mesafenin “hangi
komşudan’’ geldiğini hatırlamak ve bunu bir yerlere kaydetmek yeterli.
Her düğüm için, son noktaya olan en kısa mesafe değişmediğine göre,”o
mesafe bilgisinin geldiği komşunun hangisi olduğu’’ bilgisi de
değişmeyecektir. Ve her nokta için o “ebeveyn komşu’’ bilindiği zaman
herşey işleyip bittikten sonra en kısa yol tarifi için eldeki kayda
bakarız, ve başlangıç noktası a’dan başlayarak zıplaya
zıplaya o ebeveyn zinciri ile sona kadar geliriz. Bu değişiklikleri
ekleyince kod şu hale gelir,
import numpy as np
from memo import *
def rec_dag_sp2(W, s, t, debug=True):
parent = {}
@memo
def d(u):
if u == t: return 0
distances = [W[u][v]+d(v) for v in W[u]]
min_dist = min(distances)
parent[u] = list(W[u])[np.argmin(distances)]
if debug: print ('Geri donus,',u,'uzerindeyiz, mesafe=',min_dist)
return min_dist
return d(s), parentimport sp
dist, parent = sp.rec_dag_sp2(DAG, 'a', 'f')
print ('ebeveynler', parent)onbellekte yok - a
onbellekte yok - b
onbellekte yok - c
onbellekte yok - d
onbellekte yok - e
onbellekte yok - f
Geri donus, e uzerindeyiz, mesafe= 4
onbellekte var - f
Geri donus, d uzerindeyiz, mesafe= 3
Geri donus, c uzerindeyiz, mesafe= 10
onbellekte var - d
onbellekte var - f
Geri donus, b uzerindeyiz, mesafe= 5
onbellekte var - f
Geri donus, a uzerindeyiz, mesafe= 7
ebeveynler {'a': 'b', 'c': 'd', 'b': 'd', 'e': 'f', 'd': 'f'}Not: argmin bir liste içindeki en minimal değerin
indisini verir.
İşte sonuç. Başlangıç a, onun ebeveyni b.
b’ye bakıyoruz, onunki d. Oradan
f’ye atlıyoruz, ve sonuca erişmiş oluyoruz, en kısa yol
a-b-d-f.
Analiz
Açgözlü yaklaşımdan bu yaklaşımın farkını şimdi daha iyi görebiliriz, açgözlü teknik her düğümde en azı bizzat takip eder, ve kısayol hesabı, mesafe hesabı hep bu takip eylemi sırasın o anda yapılır, elde bir toplam vardır ve ona eklenir, vs. Bu yaklaşım daha hangi yolu seçtiği, sonradan, birkaç adım sonrasında hiçbir seçimle ilgilenmez. Dinamik Programlama ise takip etme eylemi ile hesap eylemini birbirinden ayırır, ve tümevarımsal bir tanımdan yola çıkarak, hep en kısa, en optimali bulmayı başarır.
DP algoritmasının karmaşıklığı, \(M\) tane bağlantı (edges) ve \(N\) tane düğüm için \(O(N + M)\)’dir. Yani çözüm lineer
zamandadır! Alt problemleri tekrar tekrar çözüyoruz evet, ve
@memo ibaresini koddan çıkartsaydık algoritmamızın üstel
(exponential) zamanda işlediğini görürdük, ki bu çok kötüdür. Fakat
çözülen alt problemleri bir daha çözmeyip sonuçlarını önbellekten
aldığımız için algoritma son derece hızlı işliyor.
Kaynaklar
[1] Hetland, M., L., Python Algorithms, 8. Bolum
[2] Bayramlı, Dekoratorler, Onbellek Kodlamasi, Fonksiyon Degistirmek, https://burakbayramli.github.io/dersblog/sk/2013/07/onbelleklemeyi-dekorator-ile-yapmak.html