Hesapsal Karmaşıklık Teorisi (Computational Complexity)

Bu bilim dalı algoritmaların yer ve zaman gibi kaynakları ne kadar kullandığından hareketle bu algoritmaları kategorize etmeye uğraşır. Diğer bazı amaçlar, hangi algoritmaların çözümsüz olacağı, hangi algoritmaların çok zaman alacak olsa bile, eninde sonunda bir sonuca varabileceği gibi konulardır.

Algoritma türlerinin arasındaki benzerlikleri bulmak zorluk teorisin ana eylemlerinden; mesela problem $A$ için bir algoritma yazmamız gerektiğini düşünelim, ve aynı gün kuramsal bir bilgisayar bilim makâlesinde, bizim problemin diğer bir "$B$ problemi" ile tıpatıp aynı olduğunu okuduk. Bu makâleye göre, $B$ probleminin kabakuvvet çözümünün "yavaş" olduğu belirtilmiş olabilir, ve hızlı çözümün imkansız olduğu da ispat edilebiliyor. Bu bilgiden hareketle, $A$'nın da hızlı cözümünün olamayacağını daha baştan anlarız, akıllı tahmin (heuristic) ekleyerek çözümü biraz olsun hızlandırmaya çalışabiliriz.

P (Polinom) Grubu

Bir algoritmanın P grubu içinde olduğu söyleniyorsa, bu algoritma polinom zamanda işliyor demektir, yani algoritma karmaşıklığı $O(n^2)$ gibi bir şekilde belirtilebiliyordur; polinom ifadesi herhalde $n^2$ ifadesinin bir polinom olmasından, $O(n)$, yani eleman sayısına direk orantılı / lineer zamanda işleyen algoritmalar de tabii ki bu grupta ($n^1$ de bir polinom (!) ). P grubu en hızlı işleyen algoritmalar grubudur, algoritmalarımızı bu grupta görmek isteriz, ve ona göre tasarlamaya çabalarız. En iyi bilinen, "iyi" algoritmaların hepsi bu gruptadır, mesela tüm popüler sıralama (sorting) algoritmaları, aritmetik hesaplar, lineer cebirdeki çoğu matris işlemi, kısayol bulma algoritmaları, vs.

NP-Zor (NP-Hard) ve NP-Tam (NP-Complete)

Bilgisayar bilimde öyle problemler vardır çözümlerini bulmak için mümkün girdinin tüm kombinasyonlarını denemek gerekir. 3SAT bu problemlerden biri. Diyelim ki $x_1,..,x_n$ değişkenlerini kullanıp en fazla üç öğeli, ve grup içinde VEYA ile birbirine bağlı, gruplararası ise VE ile birbirine bağlı bir ifade zinciri oluşturuyoruz.

$$ (x_1 \lor x_2 \lor \bar{x_3}) \land (\bar{x_1} \lor \bar{x_2} \lor \bar{x_3}) \land (x_1 \lor \bar{x_2}) \land (\bar{x_1} \lor \bar{x_2}) $$

ki $\lor$ işareti VEYA (OR), $\land$ işareti ise VE (AND), değişken üzerinde çizgi olması onun tersinin alınması (NOT) demek. Soru şu, bu ifadenin doğru yani 1 sonucunu vermesini sağlayacak girdiler / onu tatmin edecek (satisfy -SAT kısaltması buradan geliyor-) var mıdır? Ve bu sonuç polinom zamanda bulunabilir mi?

Bu ufak örnekte tahmin etmeye uğraşırsak, $x_1=1,x_2=0,x_3=0$ bu formülü "tatmin eder", yani üstteki ifade 1 sonucunu verebilen bir ifadedir. Fakat bu sonuca "kesinlikle" erişmek ve bunu her tür 3SAT problemi için yapabilmek için bir programın tüm girdi kombinasyonlarını denemesi gerekir. Tüm seçeneklerin denenme mecburiyeti bir problemi zor kategorisine sokar. Kısayol, cinlik, envai türden tahmin (heuristic) her zaman ise yaramaz, bazı problemlerde yarayabilir, fakat hesapsal zorluk her zaman en kötü şartın performansını baz alır.

3SAT o kadar temel bir problemdir ki, zor problemler kategorisinde temsili bir özelliği vardır. Tüm zor problemler 3SAT'a indirgenebilirler. Bu tür problemlere ayrıca NT-Tam ismi de verilir, çünkü çok zor problemleri "tam" olarak temsil ederler.

Turing Makinaları

Şimdi Turing makinalarına, onların baştan planlı (deterministic), baştan plansız (nondeterministic) şekillerinin üzerinden geçelim.

Algoritma başı sonu belli, her muhtemel seçenek için önceden belirlenmiş bir kod parçasının devreye girdiği bir veri ve eylemler dizisidir. Bu algoritmayı yazarken içinde bulunduğumuz evren, değişkenler, girdi, çıktı aletleri, eğer/eylem çiftleri, gibi kavramların olduğu bir evren. Bu dili işleten makinayı bir soyut makina olarak görelim. Fakat göreceğiz ki, halâ teorik iş yapmamız için bu makina yeteri kadar basit değildir. Kullandığımız 'esnek' dili destekleyen makinamız oldukça çetrefil hâlde. Ayrıca, dili değiştirirsek (Java yerine LISP gibi) makinın da değişmesi gerekir, bütün dilleri temsil edebilen bir makina bulamaz mıyız? Teorik iş yapabilmemiz için böyle evrensel bir makinaya ihtiyacımız var.

Dili basitleştirelim. Direk erişimli (random access) belleği olan, komutları ve verisi aynı gözüken bir makina yapalım ve onun kullandığı dili tasarlayalım. (Bu makina günümüzde kullanılan bilgisayardır).

Peki bu makina daha da basit olamaz mı?

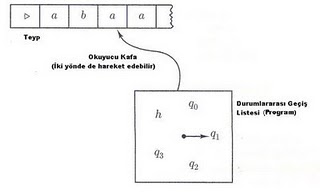
Olur. Tek bir teyp üzerinde girdisini tutan, her an, önceden belirli ve sayılı konum/durum içinde olabilen, komutlarını, durumdan/duruma geçiş listesi olarak tutan bir makina düşünelim.

Öyle gözüküyor ki, artık bilgisayar işleminin ruhuna indik. Bundan daha basit bir makina tasarlamamız mümkün gözükmüyor. Durum, geçiş, ve teyp kavramlarını kullanarak her türlü bilgisayar hesabını temsil edebileceğimizi düşünürsek (bunun ispatları yapılmıştır), en basit temsil şeklinde varmış olduğumuzu görüyoruz.

İşte bu makina, Turing makinası olarak bilinir.

Formel olarak, Turing makinası M şu dörtlüyü içerir:

$$ M = (K,\Sigma,\delta, s) $$

$K$ = makina durumu (state)

$\delta$ = gecis fonksiyonu

$\Sigma$ = teyp alfabesi

$s$: teyp verisi

Dörtlü içindeki bütün terimler birer kümedir. K terimi, M makinasının içerdiği durumların kümesi, delta bütün geçişlerin listesi, sigma, alfabe olduğu için teypin kullandığı harflerin kümesi ve s, giriş için M makinasına verilen harflerin kümesidir.

Şimdi programa dönelim: Geçiş fonksiyonu olan delta, yani program, K x Sigma ile, (K U {dur, "evet", "hayır"}) x Sigma x {Sol, Sağ, Hareketsiz} küme üyelerini birbirine eşler. Yani geçiş fonksiyonu, durum+teyp sembolu ikililerini, durum+teyp sembolu+teyp hareketi üçlülerine eşlemektedir.

Not: 'x' operasyonu, iki küme arasında kartezyen eşleme yapmaktadır. Yâni, A x B, A kümesinin her elemanı ile B kümesinin her elemanını eşleyerek, |A|*|B| sayıda yeni bir küme oluşturur. SQL dilini bilenler JOIN komutu ile bağlantı kurabilirler)

Turing makinasının işlevi, makinanın o anda gördüğü, kafasının okuduğu sembol, ve o an içinde olunan duruma göre başka bir duruma geçmek, ve (gerekiyorsa) teype yeni bir harf yazmak, sonra da teyp kafasını gene programa göre sağa ya da sola hareket ettirmekten ibarettir. Teyp kafasını hareketsiz bırakmakta mümkündür.

Bu kadar basit temel işlemlere dayanan bir modelin dünyadaki bütün algoritmaları temsil edebilmesi ilginç değil mi?

Örnek Turing makinası olarak, aşağıda teyp üzerinden verilen bir metnin palındrom olup olmadığını anlayabilen bir Turing Makinayı görebiliriz. Bu program (makina), eğer metin palındrom ise "evet" cevabı verecek, değil ise "hayır" cevabı verecektir. Palındrom metni, "arabaabara" gibi, içinde "araba" kelimesinin ters yüz edilerek yanyana konulduğu metne verilen isimdir. Palındrom tanımak çok kolay olmayıp çok zor da olmayan bir örnek olduğu için hesapsal karmaşıklık teorisi kitaplarında oldukca kullanılmaktadır [1]. Alttaki örnek ikisel veri üzerinde işliyor, yani $M(0000) = 'evet'$, $M(011) = 'hayır'$, ve $M(0110) = 'evet'$ cevaplarını hesaplayacak.

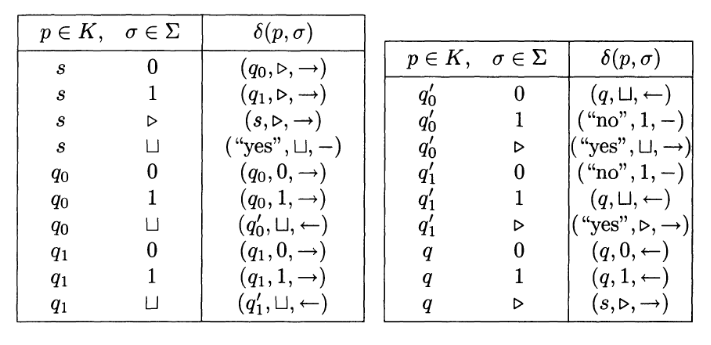
$\Sigma$ her zaman özel karakterler $\sqcup$ ve $\rhd$'yi içerir, bunlar sırasıyla "boş" ve verinin başını temsil eden ilk semboldur. Program denen şey $\delta$'dir, $\delta(q,\sigma) = (p,\rho,D)$ olarak belirtilir, yani her $q \in K$ ve o anda üzerinde olunan sembol $\sigma \in \Sigma$ için sonraki konum $p$'yi, $\sigma$ üzerine yazılacak (bir önceki silinerek) sembol $\rho$'yu, ve teyp üzerinde hangi yöne hareket edileceğini gösteren $D \in { \leftarrow, \rightarrow, -}$'yi üretir. Eğer başlangıçta isek bu sembolü silmeden hep sağa gitmek istiyoruz, o sebeple programın değişmeyen tek parçası $\delta(q,\rhd) = (p,\rho,D)$ $p=\rhd$, $D=\rightarrow$.

Program nasıl başlar? İlk önce konum $s$'dir. Girdi $\rhd$'ye getirilir, bu sembol arkasında sonlu (finite) bir karakter dizisi vardır, $x \in (\Sigma-{\sqcup} )$. $x$'e Turing makinasının girdisi adı verilir. Başta teyp kafası $\rhd$ üzerindedir.

İşleyiş şöyle devam eder: $s$ konumunda girdinin ilk sembolü aranır, bulununca bu sembol bir $\rhd$ haline getirilir (böylece sanki girdi sola doğru çekilmiş gibi olur, daha doğrusu girdinin ilk öğesini "işlenmiş" hale getirdik, onu sildik -ama konumda onu hatırlıyoruz-). Konumda hatırlamak ilk karakter 0 ise $q_0$ konumuna 1 ise $q_1$ konumuna girmek ile oluyor. Sonsuz olmayan girdi öğelerini konum üzerinden hatırlanması Turing makinalarının önemli numaralarından biridir bu arada, ve pek çok farklı yerde kullanılır. Ardından $M$ teyp kafasını $\sqcup$ bulununcaya kadar sağa doğru gönderecektir, bir kez sona gelinince en sondan bir önceki sembole bakılır. Tabii "sona gitmek" te belli programsal adımlar ile yapılıyor, ilk sembol 0'dı diyelim, sağa geldik 0 ise 0 yaz, sağa git, 1 ise 1 yaz, sağa git adımları bu gidişi hallediyorlar.

Sona gelinince akılda tutulan $q_0'$ ya da $q_1'$'e geçilir, böylece hem sona gelmiş olduğumuzu, ve başta ne okumuş olduğumuzu hatırlamış oluyoruz, sonra teyp kafasını sola hareket ettiriyoruz. Buradaki öğe hatırlanan öğe ile uyumlu ise oraya $\sqcup$ yazıyoruz, böylece bu öğeyi bir bakıma "işlenmiş" olarak siliyoruz. Eğer uyumsuzluk var ise, 'hayır' cevabı verip duruyoruz. Devam ediyorusak bu noktada eldeki dizi hem soldan hem soldan hem sağdan küçülmüş oldu, ve geri kalan veri üzerinde aynı işleme devam edebiliriz, veri küçülecek, küçülecek, eğer elde bir palındrom var ise elde hiç girdi kalmayana kadar bu işlem devam edecek.

Church-Turing Tezi

Araştırmacılar uzun süre Turing makinasından daha basit bir model bulmaya uğraştılar, ve bu uğraşıda başarısız oldular.

Daha sonra araştırmacılar, kaç değişik makina modelinin mevcut olabileceğini anlamak için, en basit Turing makinasının çözemeyeceği problemleri çözecek makinalar tasarlamaya da uğraştılar. Mesela RAM, birden fazla teyp, vs. gibi ekler koyarak, basit modeli güçlendirmeye çabaladılar. Eğer en basit modelin çözemeyeceği bir problemi çözen bir model bulsalardı, bu model yeni ve alternatif bir model olabilirdi. Yeni modelin değişik olup olmadığını nasıl anlamak için, kuramcılar indirgeme denen bir tekniği kullandılar. İndirgeme, yeni modelle kurulmuş olan makinayı, eski modelle kurulmuş makina aracılığı ile, yani onun dili ile, simule etmektir.

Bu simulasyonun 'dönüşüm' denen aşamasında, simule edilen makinanın girdisi, ötekine çok hızlı bir şekilde dönüştürülür. Hemen ardından simule eden makinaya girdi olarak verilir. Çıktı da aynı şekilde dönüştürülür.

Eğer çok hızlı (polinom zamanlı) olarak dönüşümü yapabildiysek, ve simule de çalışır ise, indirgeme başarılı olmuş demektir.

Fakat, görülmüştür ki, envai türden ekler ile güçlenen her 'sözde yeni' model en basit Turing makinasına indirgenebilmiştir. Demek ki bu 'yeni' modeller gerçekten yeni model değillerdi, ve işte bu bu sayede bilgisayarlar için en basit Turing makinasından alternatif bir model olamacağı kanıtlanmış oldu.

Bütün bu bulgulara dayanarak Church ve Turing şu tezi kabul etmeye karar verdiler.

"Bir algoritma ile, (bütün girdilerine "evet" ve "hayır" cevabı verebilen) bir Turing makinası tamamen aynıdır. Birbirleri arasında direk ilişki vardır. "

Yani, algoritma denen soyut kavram, en basit Turing makinası üzerinde yazılan bir program demektir, bütün teorik hesaplar ve kuramlar bu en basit makina üzerinden yapılabilir.

Bu ortak bilgisayar kavramında fikirbirliğine varılmasının ne kadar önemli olduğunu vurgulamak istiyorum. Teorik dünyada, 'bilgisayar' denince, formel bir kavram akla gelmelidir. En basit makinalar arasında en güçlüsü seçilerek, bu makinayı baz alan kuramların da aynı şekilde basit olması sağlanmıştır. Basitlik, bilim dünyasında önemli yer tutar.

"Her girdiye evet ya da hayır cevabı veren" makinaların özellikle belirtilmesi ilginçtir. Bunun sebebi şudur; Her Turing makınasının (yani programın) işleyişini biterek durması garanti değildir. Sonsuz döngüye giren programları hepimiz biliyoruz. Eğer evrendeki her Turing makinasını 11001010... gibi bir ikili düzen kodu ile belirtiliyorsak, bu makinalardan her biri durup, "evet" ya da "hayır" cevabı veriyor olamaz (bu söylemin ispatını algoritma çetrefilliğini işlediğimiz yazıda bulunabilir).

Church-Turing tezi, duran ve "evet" ya da "hayır" cevabı veren makinaların bir algoritma ile eşgörülmesini belirtmiştir.

Ek olarak belirtmek gerekir ki, Church-Turing tezi sadece bir tezdir, yani bir önkabuldür. Aynen matematikteki bir aksiyom gibidir, yani ispatlanmış teori değildir. Bu sebeple doğruluğu veya yanlışlığı ispat edilemez. Geometride nokta, çizgi gibi kavramların en baştan ispatsız olarak kabul edildiği gibi, Church-Turing tezi bir başlangıç önkabuludur. Bu önkabul olmadan geri kalan teorileri bir temele oturtmamız mümkün olmazdı.

Tabii, Church-Turing tezi bir tez olduğuna göre, başka bir tez gelecek olsa değişik bir bilgisayar bilim teorisi kurulabilirdi. Fakat araştırmacılar bunun mümkün olduğunu düşünmüyor.

Sonsuza Giden İkili Sayıların Kümesi

Aşağıda gösterilen küme, sayılamayan sonsuz bir kümedir.

B =
{1101 ....... }
{1011 ....... }
{1110 ....... }
{.100 ....... }
{.011 ....... }
...

Teori: B sayılamayan sonsuzluktadır.

İspat:

B'nin sayılabilir olduğunu farzedelim.

Kullanılan matematiksel teknik: Bir teorinin "karşıtının" doğru olduğunu, yani B'nin sayılabilir bir sonsuzluk olduğunu farzedip yola devam eder, ve anlamsız / saçma / absürt bir sonuca varırsak, tersini farzettiğimizi teori doğru demektir. Bu, yanlışın yanlışlığının doğruyu vermesidir bir anlamda.

Bu teknik, matematikte "karşıtlık ile ispat etmek" diye bilinir. Teorinin tersini kabul edip yanlış bir sonuca vardıysak, demek ki teori doğrudur .

Devam edelim. B'nin sayılabilir olduğunu farzettiğimize göre, aşağıdaki gibi bir eşleme mümkün olabilir.

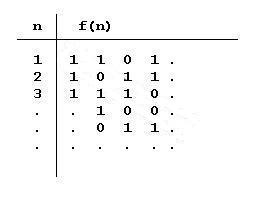
Şimdi, doğal sayılar ile olan eşlemeyi yanlış çıkartmak için öyle bir sayı bulacağız ki, hiçbir n ile eşlenemeyecek.

Bu sayı, köşegen üzerindeki sayının ikili aritmetiğe göre tam tersi olsun (köşegen aşağıda gösterilmiştir)

Yani köşegendeki 1010.. yerine, 0101... kullanacağız. Bu sayı, bir n ile eşlenebilir mi?

Hayır! Neden olduğunu görelim. Bu eşlemenin imkansız olmasının sebebi, sol tarafta 1,2,..n diye giderken, n'in karşısındaki f(n)'in (terslik kuralımız yüzünden) n'inci değerinin her zaman gerekenden ters bir değer olacağıdır.

Halbuki, elimizde sonsuz tane 0 ve 1 var, ve elimizdeki 0101.. değerini bir yerlere koyabilmeliydik. Fakat elimizdeki gayet masum ve basit kurala göre bile bunu yapamıyoruz. Demek ki, başta yapılan faraziye, yanlış idi, bu da teorinin doğruluğunu ispatlar. B sayılamayan büyüklükte bir sonsuz kümedir.

Sonsuzluklar Arasındaki Farklar

İki sonsuzluk arasındaki en bariz fark, bir sonsuzluğun sayılabilir ötekinin de sayılamayan türden olduğu zaman ortaya çıkar. Sayılabilen sonsuzlukları tanımlamak için, ünlü matematikçi Kurt Gödel, incelediği kümeyi doğal sayılar ile eşleme tekniğini denedi. Doğal sayılar bildiğimiz gibi 1'den başlayarak sonsuza kadar birer birer artan tam sayıların kümesidir.

Sayılabilir Sonsuzluklar

Zaten herhangi bir şeyi sayarken de yaptığımiz bu değil midir? Parmakla gösterip, söyleriz "bir..iki..üç...vs.", ve kullandığımız bütün bu sayılar birer doğal sayıdır. Yani sayarken biz de gösterdiğimiz şeyi, bir doğal sayı ile eşleriz.

Bu eşlemenin geçerli olabilmesi için, en güçlü matematiksel hâlinde olması gerekiyor, yani bize lazım olan birebir ve örten türden bir eşlemedir... A ve B kümesi düşünürsek; Birebir eşleme, iki değişik A elemanının hiçbir zaman aynı B elemanına eşlenmediği zaman ortaya çıkar, örten eşleme ise, B'nin bütün elemanlarının A'nın bir elemanı ile muhakkak eşlendiği zaman ortaya çıkar.

Bu iki tür eşlemenin olduğu zaman, elimizde tekabül etme (correspondence) ilişkisi çıkar.

Şimdi tekabül tekniği kullanarak örnek kümeleri inceleyelim: Mesela, 2,4,6,... olarak ikişer ikişer artan sayılar kümesi sayılabilir bir sonsuzluk mudur?

Bu soruyu, yeni bilgilerimiz ışığında değiştirerek tekrar soruyoruz; Doğal sayılar ile {2,4,...} kümesi arasında ilişki varmı dır?

Ek not: Lise matematiğinden hatırlayacağımız fonksiyon kavramı, aslında bir tekabül ilişkisidir.

Demek ki, doğal sayılar ile {2,4,...N} arasında bir fonksiyon bulabilirsek, tekabül ilişkisini kurmuş olacağız, ve {2,4,...N}'in sayılabilir bir küme olduğunu ispatlamış olacağız.

Bu fonksiyonu bulmak oldukça basit: f(x) = 2x. Demek ki {2,4,6..} kümesi sayılabilir bir sonsuzluktur.

Sayılamayan Sonsuzluklar

Gerçek sayılar, noktadan sonra kesire devam eden sayılardır, mesela pi sayısı 3.1415926.. ya da 2'nin karekökü 1.4142135... sayıları gerçek sayılardır. Cantor, R kümesinin sayılamaz olduğunu köşegenleştirme (diagonalization) tekniğini kullanarak ispat etmiştir.

Teori: Gerçek sayılar kümesi R (real numbers), sayılamaz bir kümedir.

İspat: R'ın sayılamaz olduğunu ispat etmek için, R ile N (doğal sayılar) arasında tekabül ilişkisi olmadığını ispat etmek zorundayız. İspat, karşıtlık ile ispat etme tekniğini kullanacak. Düşünelim ki, N ile R arasında f denen bir tekabül ilişkisi mümkün. Bizim yapmamız gereken, f'in gerektiği gibi çalışamacağını ispat etmekten ibaret.

F'in doğru bir tekabül ilişkisi olabilmesi için, f bütün N'in elemanlarını, tüm R elemanları ile eşlemelidir. Ama biz öyle bir x bulacağız ki, bu x hiçbir N elemanı ile eşlenemeyecek. Aradığımız karşıtlıkta işte bu x olacak.

Bu x'i arayıp bulamayız tabii, ama inşa edebiliriz.

Şimdi, tekabül ilişkisinin olduğu farzından yola çıkarak, aşağıdaki türden bir ilişkinin mevcut olduğunu varsayalım.

$$ \begin{array}{cc} n & f(n) \\ \hline 1 & 3.14159 \dots \\ \hline 2 & 55.555555 \dots \\ \hline 3 & 0.12345 \dots \\ \hline 4 & 0.5000000 \dots \\ \hline \dots & \dots \end{array} $$

Bu tekabül ilişkisi, f(1) = 3.14159...., f(2) = 55.55555..., f(3) = .. .olarak devam ediyor. Yani, f işlevi 1 sayısını 3.14159 ile eşliyor, 2 sayısını 55.55555 ile eşliyor, vs.

Baştaki farzla ilerleyip geri kalan sonuçları patlatmak için, amacımız f(n)'in üyesi olamayacak bir x bulmak idi. Bunun için şöyle bir x kurgulayabiliriz.

X'in inşa kuralını şöyle saptayalım: X'in 1. basamağındaki sayı, f(1)'in noktadan sonraki 1. basamağındaki sayıdan farklı olsun. Ne olursa olsun (önemli değil) ama farklı olsun. Yukarıdaki f(1) örneğinde bu sayı 1 (3.14159..), o zaman x'in noktadan sonraki 1. sayısı, 1'den farklı olması gerekiyor; mesela, rasgele seçiyoruz, 4.

Aynı şekilde, x'in f(2)'de olamamasını zorlamak için, x'in 2. basmağındaki sayının f(2)'nin 2. basamağındaki sayıdan farklı seçiyoruz. Yani, 5 yerine (55.55555..) diyelim 6.

Gene aynı şekilde, x'in f(3) için, 3 yerine 4 seçebiliriz, vs..

Bu şekilde f(n)'in köşegeni üzerinde devam ederek bir x oluşturmuş oluruz.

$$ \begin{array}{cc} n & f(n) \\ \hline 1 & 3.[1]4159 \dots \\ \hline 2 & 55.5[5]5555 \dots \\ \hline 3 & 0.12[3]45 \dots \\ \hline 4 & 0.500[0]000 \dots \\ \hline \dots & \dots \end{array} $$

x = 0.464...

X'in f(n)'in üyesi olamayacağını bu şekilde ispatlamış oluyoruz, çünkü x'in n'inci basamağı, f(n)'in noktadan sonraki n'inci basamağından her zaman değişik olacaktır.

Not: Biraz daha görsel olan ispatlar, şunu da ekleyebiliyor: X'i f(n) içine sokuşturmuş olduğumuzu düşünelim;

$$ \begin{array}{cc} n & f(n) \\ \hline 1 & \enspace 3. [1]4159 \dots \\ \hline 2 & 55.5[5]5555 \dots \\ \hline 3 & \enspace 0.12[3]45 \dots \\ \hline 4 & \enspace 0.500[0]000 \dots \\ \hline \dots & \dots \\ \hline \dots & 0.464 ??? \end{array} $$

Soru işareti yerine hangi sayı gelmelidir? :) Soru işareti yerine istediğiniz sayıyı koyalim, bir taraf o sayıyı öyle kabul etmekte, x sırası ise ne olursa olsun o sayı olmasın (!) demektedir. Bu bir çakışma, uyuşmazlı, absürdlük ve saçmalıktır. Demek ki baştaki faraziyemiş yanlıştır. Demek ki, R kümesi olan f(n), doğal sayılar (n) ile eşlenemiyor; O zaman R sayılamayan büyüklükte sonsuz bir küme olmaktadır.

Durmayan Turing Makinaları Var mıdır?

Bilgisayar bilimde, bir dil (language) ile algoritma (Turing makinası) arasında çok sıkı bir bağlantı vardır.

Algoritma, belli bir problemi çözmek için yazılır. Bu problemi çözmek demek, önceden kararlaştırılmış bir alfabe üzerinden oluşturulabilecek bir girdinin işlenmesi, ve bu girdiye ve programın mantığına göre bir cevabın verilmesidir.

Algoritma ile eş görülen Turing makinalarının yaptığı (bkz. Church-Turing tezi), girdiye "ret" vermek, ya da "kabul" etmektir.

O zaman, bir Turing makinasının kabul ettiği tüm girdilerin toplamını düşünürsek; bu toplama bir dil diyebiliriz.

Formel olarak

$M = (K,\Sigma,\delta,s)$

$\Sigma$: Teyp Alfabesi

$\Sigma^\ast$: Teyp alfabesi ile oluşturulabilecek tüm girdilerin kümesi

$s$: Teyp verisi

$L \in \Sigma^\ast$, ki $x \in L$, $M(x)='evet'$, ve $x \cancel{\in} L$, $M(x)='hayır'$ olacak şekilde.

Demek ki, bir evet/hayır türünden karar problemini, aynı zamanda "bir dilin karar verilme" problemi gibi de görebiliriz. Bilgisayara verilen girdiyi (bir dile ait olan bir girdiyi) anlayabiliyor muyuz? Anlamaktan öte, evet ya da hayır diyebiliyor muyuz? Verilen girdinin, beklediğimiz dile ait olup olmadığına kesin evet ya da hayır diyebiliyor muyuz?

Diller, Problemler

Bunu takiben şu soru sorulabilir: Bütün bunlar iyi de, bilgisayarların işi çoğu zaman evet/hayır cevabı veren programlar değil ki. Çoğu problem, hesaplanmış bir değer istiyor, bir sonuç, çıktı veriyor. Dünyadaki her problemi bir karar problemine çevirebilir miyiz?

Bu da kritik bir sorudur. Bunun da cevabı da "evet" olacak. Mesela bir optimizasyon problemini düşünelim. Şu ünlü seyahat eden satıcı problemi. N sayıda şehir arasındaki uzaklıklar biliniyor, bütün şehirleri ziyaret etmek kaydıyla, en kısa katedilebilecek yolu bulmamız lazım. Yani cevap, en kısa olan güzergahın raporudur.

Başlangıçta evet/hayır cevabı verilmesi mümkün gözükmeyen bu problemi, aslında bir eşik değeri vererek bir karar problemine dönüştürebiliriz. Yani, "en kısa yolu bul" yerine, "katedilen en kısa yol 1-4-3-3 şehirleri mi?" sorusuna evet ya da hayır cevabı verilmesi gibi.

Her Problem = Dil Ama Her Dil=Problem Mi?

Bu kadar girişi, bir problemin (makinanın) bir dil ile aynı olduğunu belirtmek için yaptık. Fakat bunun tersi, her zaman geçerli değildir.

Dünyadaki her dile karar verebilen bir Turing makinası olmayabilir.

Bu uyuşmazlığın sebebi ne olabilir?

Basit bir sayı farkı bu uyuşmazlığa yol açacaktır. Eğer evrendeki tüm mümkün dillerin sayısı, tüm mümkün Turing makinalarından fazla ise, demek ki bazı diller için Turing makinası olamaz, ve bu diller karar verilen diller kategorisine giremezler.

İyice kafaların karıştığını görür gibi oluyorum. Tüm diller derken bir sonsuzluktan bahsediyoruz, aynı şekilde tüm Turing makinaları derken de sonsuzluktan bahsediyoruz.. Bir sonsuzluk öteki sonsuzluktan nasıl büyük olabilir?

Evet olabiliyor! Bazı sonsuzlukların bazı sonsuzluklardan daha büyük olduğu matematiksel olarak ispatlandı, ve tabii ki bu çok büyük bir buluş oldu.

Bu yazıda numaralar üzerinden gördüğümüz örnekte olduğu gibi, tüm Turing makinalarının sayılabilir olduğunu, ama tüm dillerin sayılamayan kadar olduğunu ispatlayabilirsek, aradaki bariz farktan hareketle, bazı dilleri karar verebilecek bir Turing makinasının olamayacağını da ispatlamış oluruz.

Teori: Her dil karar verilebilen bir dil değildir.

İspat: Bütün Turing makinalarının sayılabilir kadar olduğunu biliyoruz. Turing makinası bir program olduğuna göre, her programın bir metin olarak kodlanması mümkündür. Bu kodlamayı ${0,1}$ gibi bir alfabe ile yapacak olsak, tüm Turing makinaları ${0,1}^\ast$ kümesine dahil olduğunu söyleyebiliriz. ${0,1}^\ast$ kümesi, ${0,1,00,01,11,000,...}$ olarak sonsuza giden bir kümedir. Bu kümenin içinden geçerli olmayan (bozuk) Turing makinalarını atsak, geriye kalan hâla sayılabilir bir sonsuzluktadır.

Şimdi, tüm dillere dönelim. Bir dil, mesela gene aynı sigma alfabesi üzerinde ${0,1,00,01,11,000,...}$ olarak giden bir kümede "sadece 1 ile başlayan metinler" olabilir. Aynı şekilde "sadece 0 ile başlayan metinler" bir başka dil olabilir, vs. Yani, sayılabilir sonsuz olduğunu bildiğimiz ${0,1}^\ast$ üzerinden, sonsuz kadar altküme oluşturuyoruz, tüm diller işte bu kümede oluyor.

Bu yeni küme, sayılamayan bir sonsuzluktur. İspat için, yeni kümeyi, B adını vereceğimiz sayılamayan sonsuz başka bir küme ile birebir ve örten türden eşleyelim.

B kümesi, sigma alfabesi üzerinden yarattığımız ve her bir üyesi sonsuza giden, ayrıca bu üyelerden sonsuz kadar olan bir kümedir.

Eğer eşleme başarı ile sonuçlanırsa, tüm dillerin de sayılamayan kadar sonsuz olduğu ispatlanmış olacaktır.

Aşağıda bu eşlemenin bir örneğini görüyoruz. A ile gösterilen bir dildir. A dili, 0 ile başlayan bütün ikili düzenli sayıların dili olsun. Şimdi, bu dilin elemanlarına tekabül eden hemen altındaki Xa sırasına bakın. Bu sırada, eğer bir öğe o dile ait ise, bu öğenin o sıradaki bit değeri 1 olacak. Ait değil ise 0.

Nereye gelmeye çalıştığımızı herhalde görüyoruz. $X_A$ numarasının tamâmı, A dilinin bir nevi "temsilci numarası" olmaktadır. Aynı şekilde "1 ile başlayan metinlerin toplamı olan dil"'in temsilci no'su başka olacaktır (mesela $X_C$). Temsilci no'su, aynen B kümesinin elemanları gibi, sonsuza giden bir ikili sayıdır. Bütün dillerin temsilci no'larının kümesi, B ile tekabül eden bir ilişki içindedir.

Demek ki bütün diller sayılamayan sonsuzluktadır, çünkü B'nin sayılamayan sonsuzlukta olduğunu ispatlamıştık. Kıyasla, Turing makinaları sayılabilir sonsuz olduğuna göre, aradaki fark, karar verilemeyen diller olacaktır. Bu dilleri karar verebilen Turing makinasının yazılması mümkün değildir.

Kaynaklar

[1] Papadimitrou, Computational Complexity